Task Planning for Transportation of Multiple Objects by Dual Robots Using Cloud Computing

Abstract

In this paper, the application of cloud computing in the field of robotics is described. Dual robots are assigned the job of picking up objects lying on the floor and to keep them in the given spaces. In the co-operative environment both the robots try to follow their route of shortest path till such situations arise when either the object or the space has been exhausted. Then the robot searches for the next nearest object or space or the remaining object or space and act accordingly. Due to simultaneous movement of the dual robots, there may be collision between the two robots. Detection of whether there is any collision or not is also described.

Keywords

Cloud Computing, Cooperative Environment, Dual robots, Object, Shortest Path

Introduction

The key reason of utilizing robots in industry is improving the production efficiency. The efficiency depends upon the production process which again depends upon the movement of the robots. Therefore, a lot of efforts are given for making robots more productive: Making efficient control [1], optimizing trajectories by optimizing velocity profiles [2] or end-effecter path [3], and planning collision-free paths [4]. Mostly these approaches are movement oriented. However, there a problems consisting of a number of tasks and the robot's applications in industry is to sequence them for optimization of path or resources. The easiest way to solve the task sequencing problem is to model it as the Traveling Salesman Problem (TSP) [5]. The goal of the TSP is to find a minimal-cost cyclic tour through a set of points such that every point is visited once. Multi-goal planning is another problem that considers obstacles in the environment; therefore, a collision-free path is the output. Task sequencing/scheduling [6,7] may or may not consider obstacles, therefore, the output in either case is a sequence or a path. There are several recent surveys that cover the related domains, e.g., multi-robot patrolling algorithms [8], assembly process planning [9], methods to solve Traveling Salesman Problem [10] and coverage path planning for robotics [11]. This paper provides a related combinatorial TSP-like problem that is applied in robot task sequencing.

In multiple robots task planning, the tasks have to be distributed among robots. One of the first to address this problem was Maimon [12]. He proposed the robot task-sequencing planning problem. Later, Zhang, et al. [13] proposed the approach for task allocation for a team of robots. The Stochastic Clustering Auction technique by Zhang, et al. [14] was used in this approach. This optimizes using the greedy principal, making worse steps for avoiding the local minima. The general principal is to re-cluster the tasks until termination condition is satisfied. If the cluster is better than the previous one, then it is accepted as the current one, by following Simulated Annealing strategy.

The task-level planning defines the robot actions by their interactions with objects. Often the final goal is known. The task level planning has to find a sequence of actions that a robot has to perform to change the environment from the initial state to the goal state. Every single action is then planned with domain dependent planner. Cao, et al. [15] proposed a net called AND/OR used for reasoning about geometrical task constraints. The general idea is to map proposed net to Petri net. Then, the solution search is performed by building a reachability tree from the Petri net. Later, Chien, et al. [16,17] proposed the efficient way to incorporate the domain information into the planner for the indoor robot scenario. The data is represented with object-oriented model. This model includes relation between objects, categories and physical laws. Task-level planning was also applied to mobile robotics by Galindo, et al. [18], where the hierarchical planning technique was proposed to reduce the computational expenses. In task sequencing, the tasks are areas that have to be visited, but not the objects with its handling features as in task-level planning. However, task sequencing problem may allow partial order of the sequence.

Often, researchers observe task-level and path planning as a separate problem. However, in real life, the plan created by the task-level planner often cannot be executed due to the failure of the path-planner. In that case, the task-level planner has to construct a new plan. Therefore, it is essential to design a task-level planner in combination with a collision-free planner. Bhatia, et al. [19] proposed the architecture that allows combining task-level planning with low-level motion planning by introducing new synergy level. Gaschler, et al. [20] proposed the knowledge volume approach. The main idea was to make an intermediate stage between continuous robot motions and symbolic planning.

In 2010, the term "Cloud Robotics" was introduced by James Kuffner at Google to describe how the Internet helps in massively parallel computation and sharing of vast data resources [21]. It is very much related to earlier work on "Remote Brained" robots [22]. It is for this type of connectedness that Steve Cousins, former CEO of Willow Garage, conceptualized the statement: "No robot is an island." The autonomous car built by Google exemplifies the idea. It utilizes maps and images collected and updated by satellite, Street-view, and crowd-sourcing from the network to facilitate accurate localization. Kar, et al. [23] utilized the concept of cloud in Task planning and sequencing for single robot without any constraint, with priority constraints[24] and particular jobs in particular spaces constraints [25]. Kar, et al. then extended the concept of cloud in Task planning and sequencing for dual robots without any constraint [26], with particular jobs in particular spaces constraints [27,28] and priority constraints [29,30].

After studying the above-mentioned papers we can conclude that by developing Task-planning algorithm using Cloud computing, we can make the robots perform the tasks and we can simulate the environment through some programming language to graphically show the traversal of the robots. We can even develop an algorithm to prevent the robots from colliding with each other. To the best of our knowledge, there is no research work that covers the task sequencing problem for dual robots using Cloud computing.

Problem Definition

Dual robots have been assigned the work of picking up multiple objects from a plane area and placing them in some given spaces without any constraints. A separate computer system will communicate with both the robots and determines the routes from the locations of the robots, the objects and the spaces. Cloud Computing can be used for this purpose. The problem is to find the routes for the robots for performing the tasks in the shortest possible time.

The object that lies at the minimum distance of the starting point of each robot is to be found out by calculating the distances of all the objects from each robot. If the same object is at the minimum distance from each of the two robots then the robot that is at minimum distance from the object will go for the object and the other robot will go for the object that is at the next minimum distance from it. When one robot picks up an object, it will keep the object in the space that is nearest to it and empty. When one robot reaches a particular space and keeps the object there, it will go for the next object that is nearest to it and not picked up by any robot. The process is repeated till all the objects are picked up and placed.

Methodology of Solving the Problem

Assumptions for the work

i. Both the robots are assumed to be point robots (i.e. with negligible dimensions).

ii. Four objects and four spaces are taken as a case study.

iii. Objects may be picked up in any order.

iv. Only one object can be placed at one space.

v. Any object may be placed at any space.

vi. Both the robots will start at the same time and move with same speed.

vii. Both the robots are initially at reasonably close distances from the objects.

viii. The time for picking up an object from source and placing the object at the destination by the robot is negligible.

ix. The initial location of Robot1 is assumed to be the origin and is denoted by R1.

x. The initial location of Robot2 is assumed as (120, 0) and is denoted by R2.

Algorithm: Stage by stage minimum distance

The object that lies at the minimum distance of the starting point of each robot is to be found out by calculating the distances of all the objects from each robot. If the same object is at the minimum distance from each of the two robots then the robot that is at minimum distance from the object will go for the object and the other robot will go for the object which is at the next minimum distance. When one robot picks up an object, it will keep the object in the space that is nearest to it and empty. When one robot reaches a particular space and keeps the object there, it will go for the next object that is nearest to it and not picked up by any robot. The process is repeated till all the objects are picked up and placed.

Algorithm: Stage by Stage Minimum Distance

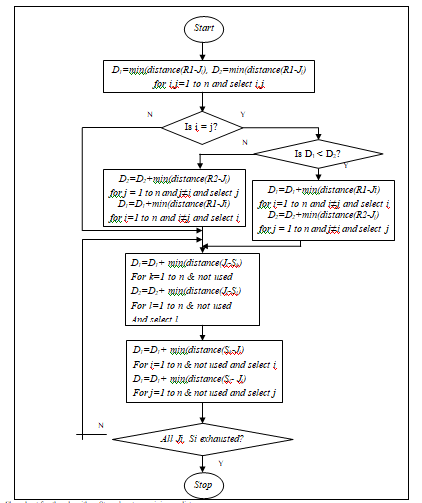
Flowchart for the algorithm: Stage by stage minimum distance

Demonstration of the algorithm with test case 1

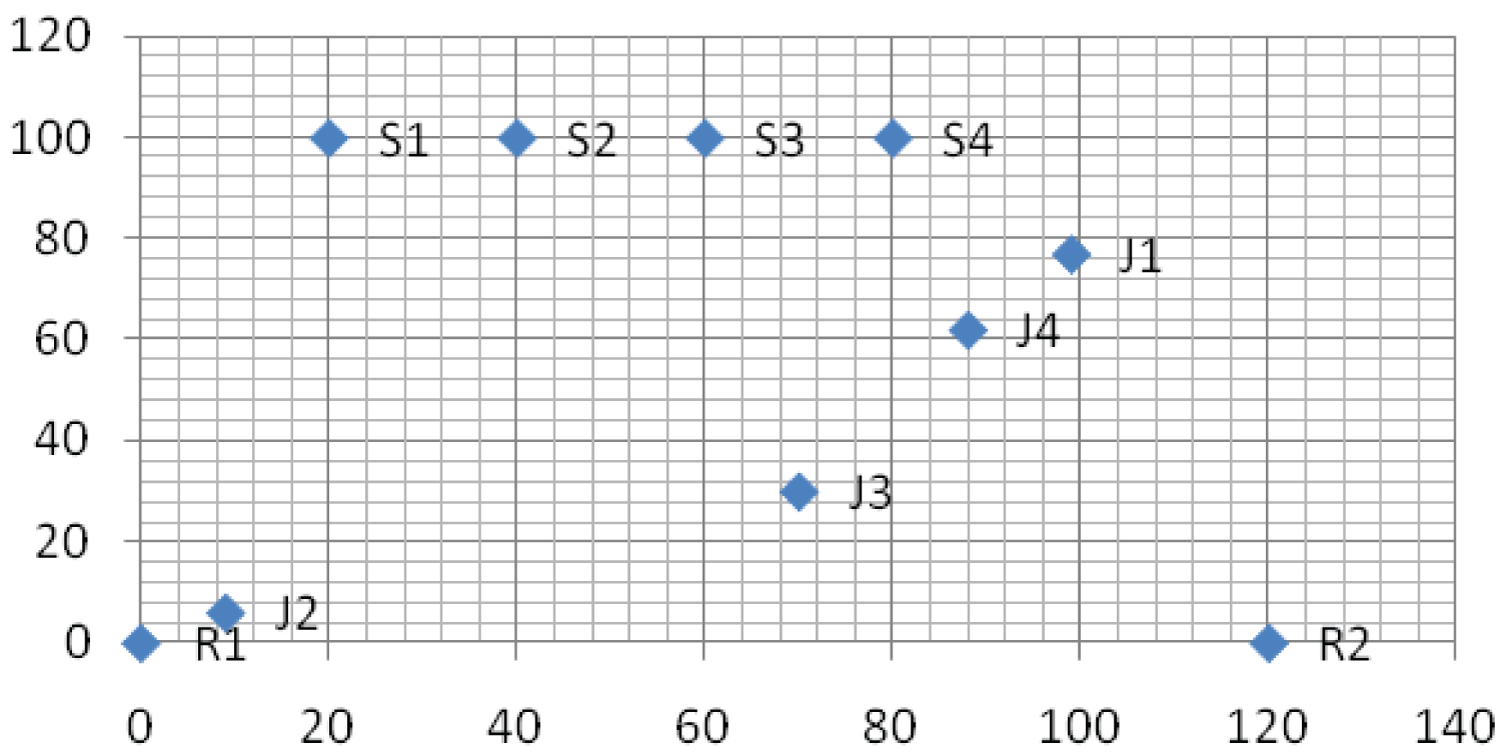
For demonstration of the algorithm with a Test Case, four objects are considered, which are to be kept at four spaces. The current location of the objects are denoted by Ji where i = 1 to 4 and the locations where the objects are to be kept are denoted by Si where i =1 to 4. In the Test Case, the locations of objects and spaces are shown in Table 1 and Table 2.

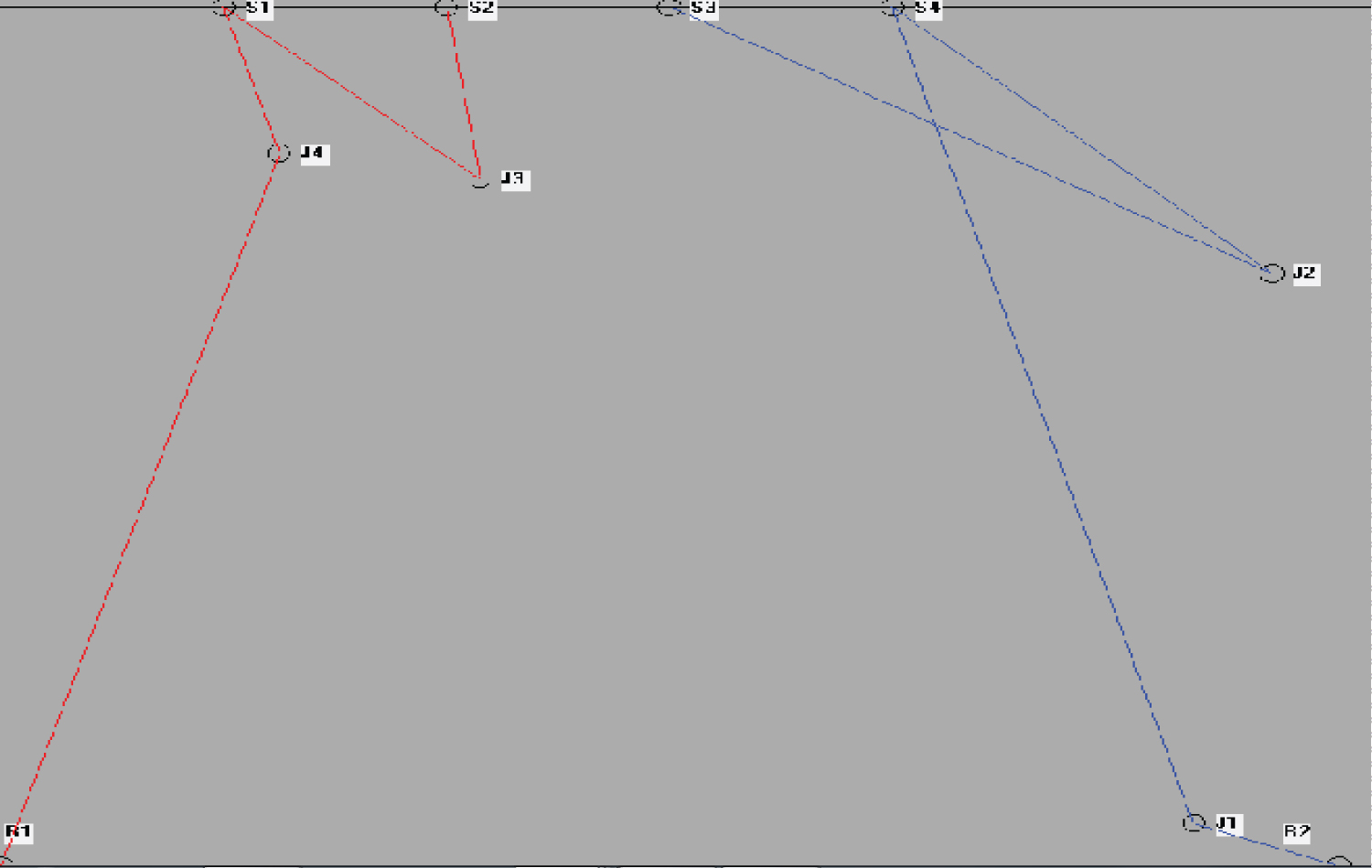
The layout of the workspace showing the locations of the robots, the objects and the spaces are represented in the Figure 1.

As shown in Figure 1, the initial positions of the robots Robot1 is (0,0) and Robot2 is (120,0). As both the robots are assumed to move with same speed, the routes of the robots can be determined on the basis of distances traversed by them to reach the objects or the spaces. The distance matrix for R1 and R2 is given in the Table 3.

The two robots are working simultaneously. The path of both the robots along with the distances at each stage of operation and the cumulative distances are calculated are given below:

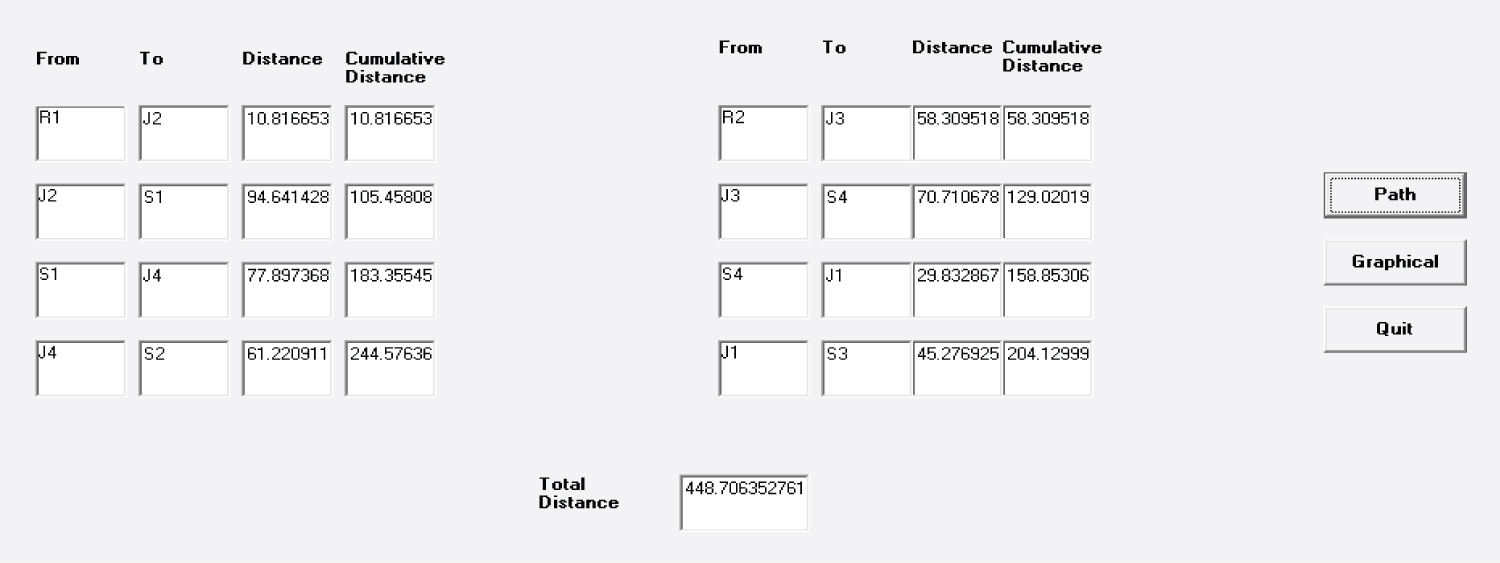
At the beginning, D1 = 10.82(R1-J2) and D2 = 58.31(R2-J3). So, Robot1 moves to J2 and Robot2 moves to J3. From J2, S1 is nearest, Robot1 moves to S1 to keep the object. From J3, S3 and S4 are nearest. Robot2 chooses S4 (or S3) to keep it. From S1, J4 is nearest, Robot1 moves to J4 to pick it up. From S4 (or S3), J1 is nearest, Robot2 moves to J1 to pick it up.

From J1, S3 (or S4) is nearest, Robot2 moves to keep the object at S3 (or S4). From J4, only S2 is lying vacant and so Robot1 has no other choice but to keep the object at S2.

Thus the routes of the robots are:

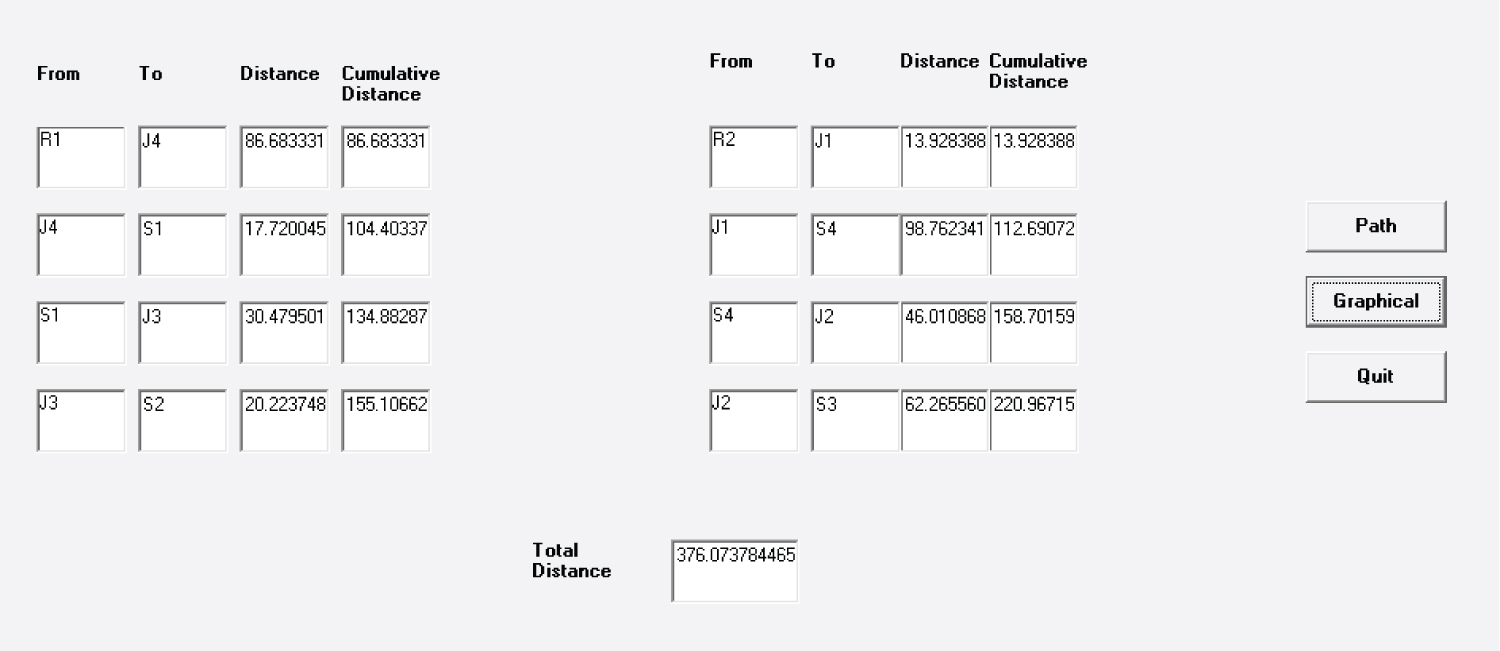
R1-J2-S1-J4-S2 and R2-J3-S4-J1-S3 or

R1-J2-S1-J4-S2 and R2-J3-S3-J1-S4

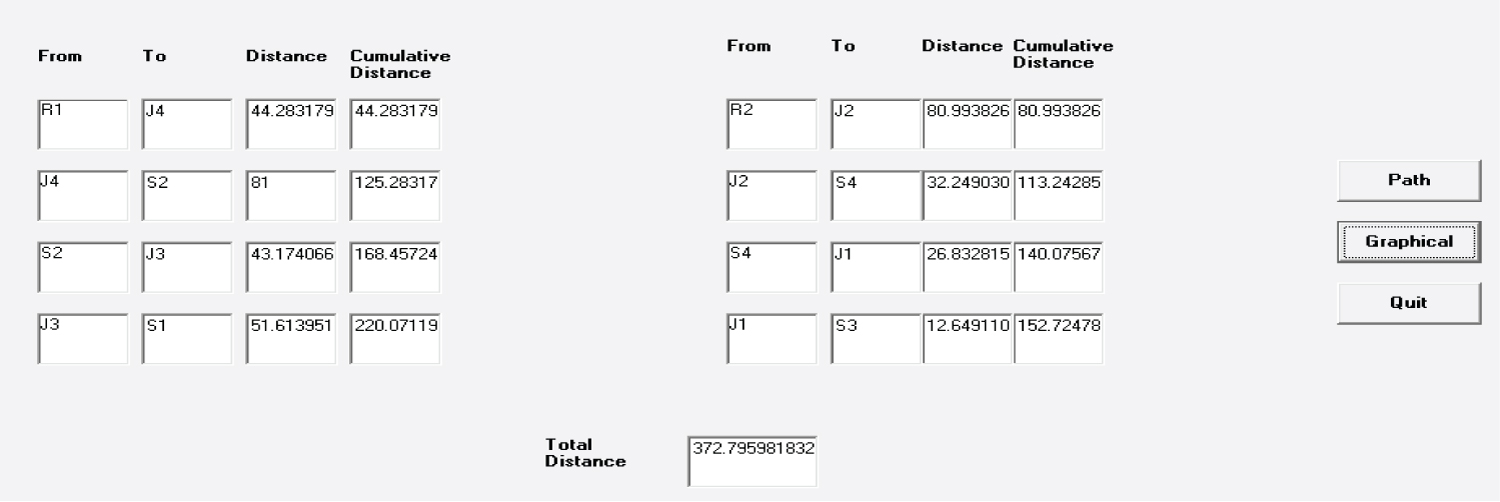
The routes of the two robots along with the distance at each stage and the cumulative distances are calculated and shown in Table 4a and Table 4b for the two cases.

So, the objects will be kept at spaces as show in Table 5.

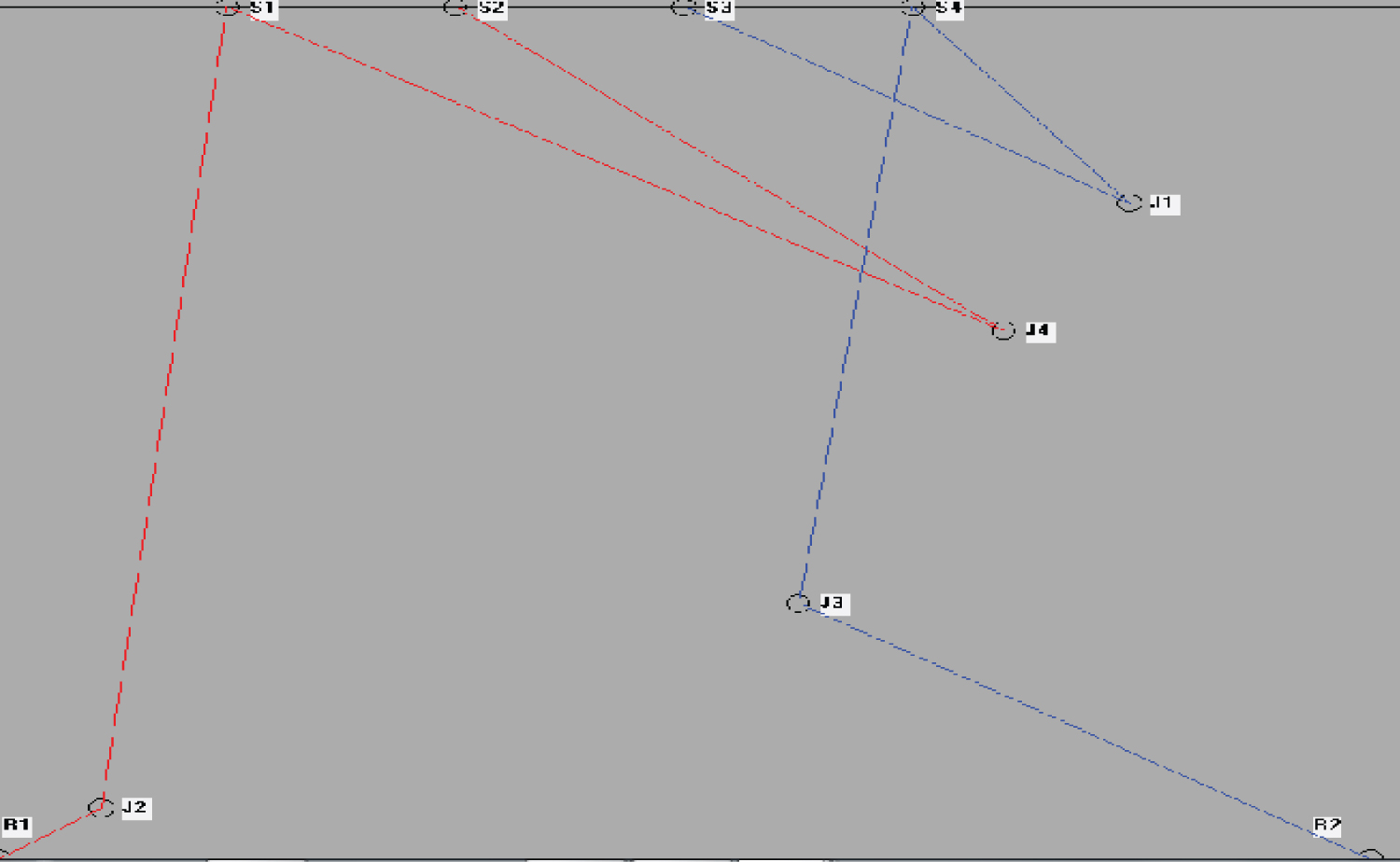
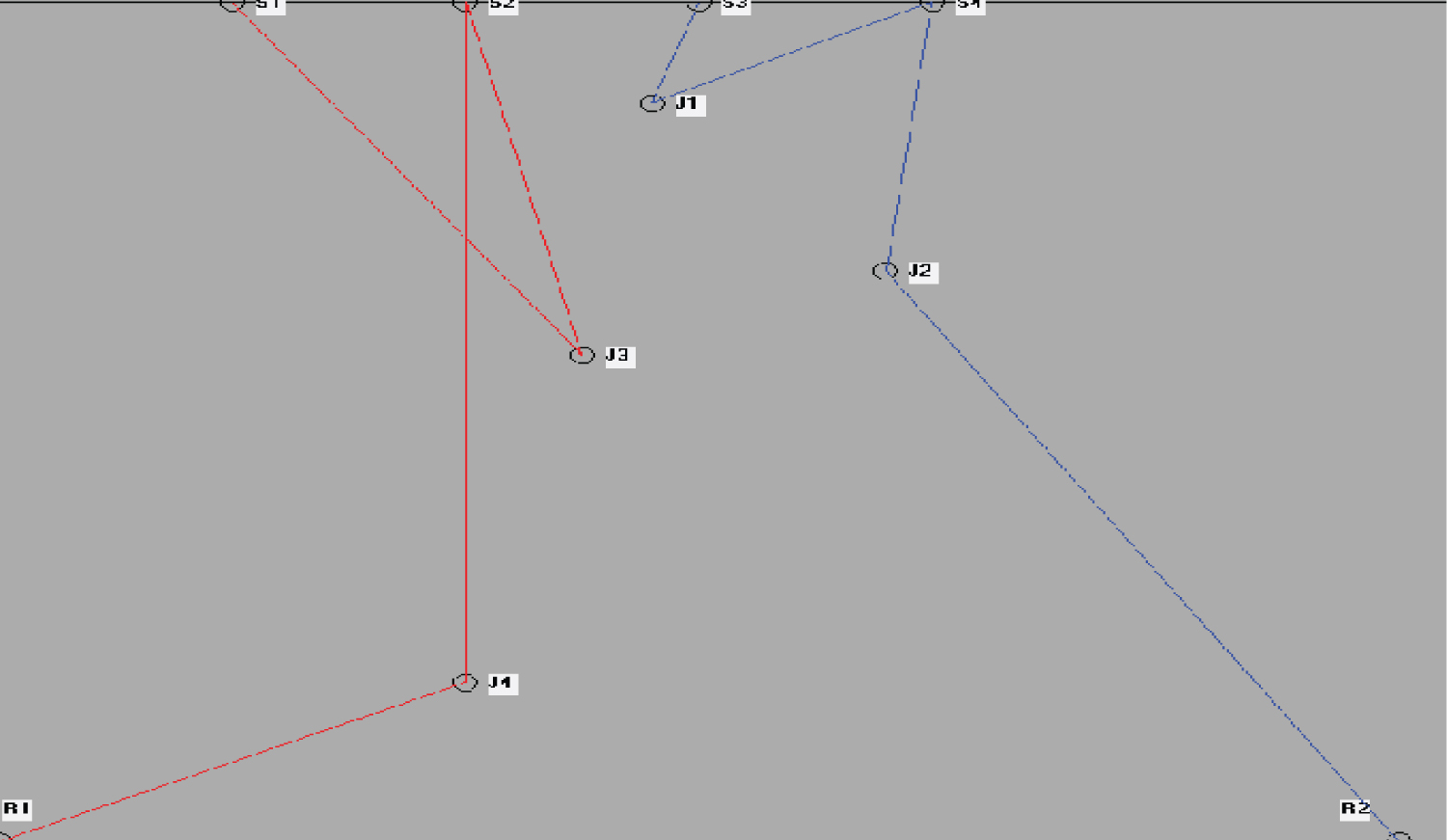
The steps of the robot movement obtained by the program are shown in Figure 2 for the case discussed. The graphical view of the path of the two robots is given in the Figure 3.

Demonstration of the algorithm with test case 2

The program has been tested for another case with different object locations. Some cases with results are shown in Table 6, Table 7, Table 8 and Table 9, Figure 4 and Figure 5.

Demonstration of the algorithm with test case 3

Another case with results is shown in Table 10, Table 11, Table 12 and Table 13, Figure 6 and Figure 7.

Algorithm: Detection of collision

Algorithm: Detection of Collision

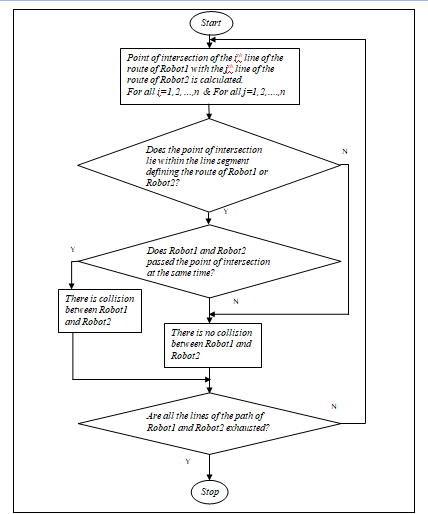
Flowchart for the Algorithm: Detection of Collision

Demonstration of the algorithm with test case 1

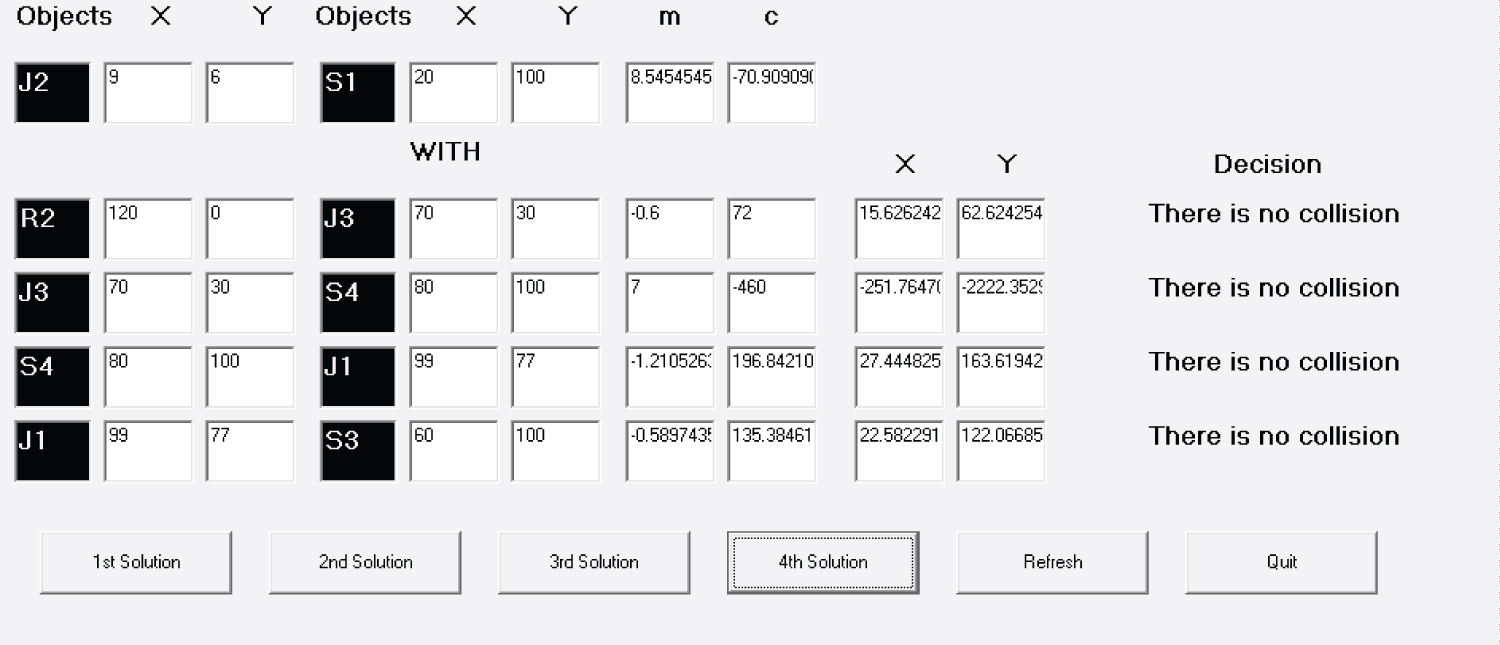
The robot1 traverses the path R1-J2-S1-J4-S2. It moves through the line segments R1-J2, J2-S1, S1-J4 and J4-S2. The robot2 traverses the path R2-J3-S4-J1-S3. It moves through the line segments R2-J3, J3-S4, S4-J1 and J1-S3. We compare each line segment of the path of robot1 with each line segment of the path of robot2 for intersection.

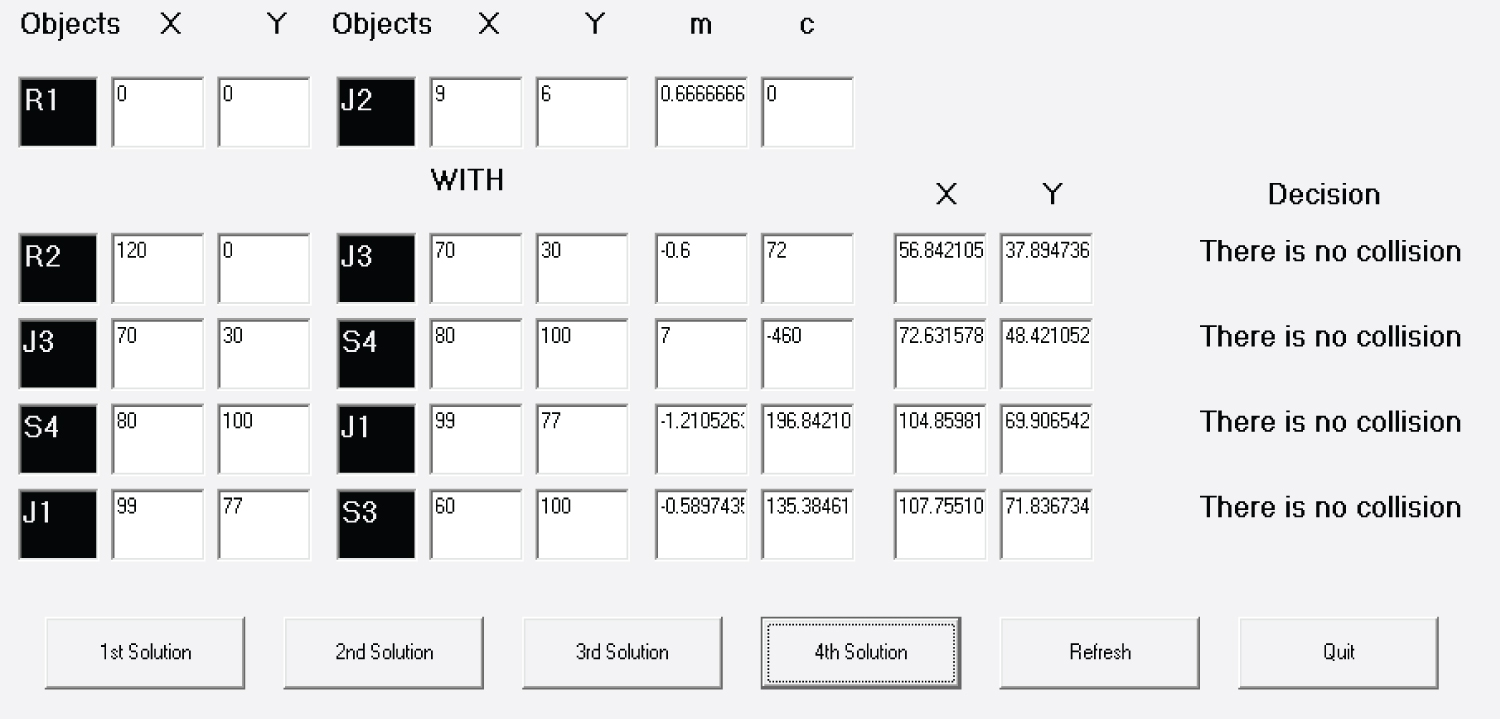
From Figure 8, it is found that the line R1-J2 will intersect the line R2-J3 at the point (56.84, 37.89) which does not lie between the points R1 and J2. So there is no collision.

The line R1-J2 will intersect the line J3-S4 at the point (72.63, 48.42) which does not lie between the points R1 and J2. So there is no collision.

The line R1-J2 will intersect the line S4-J1 at the point (104.86, 69.91) which does not lie between the points R1 and J2. So there is no collision.

The line R1-J2 will intersect the line J1-S3 at the point (107.76, 71.84) which does not lie between the points R1 and J2. So there is no collision.

From Figure 9, it is found that the line J2-S1 will intersect the line R2-J3 at the point (15.62, 62.62) which does not lie between the points R2 and J3. So there is no collision.

The line J2-S1 will intersect the line J3-S4 at the point (-251.76, -2222.35) which does not lie between the points J2 and S1. So there is no collision.

The line J2-S1 will intersect the line S4-J1 at the point (27.44, 163.62) which does not lie within the points J2 and S1. So there is no collision.

The line J2-S1 will intersect the line J1-S3 at the point (22.58, 122.07) which does not lie within the points J2 and S1. So there is no collision.

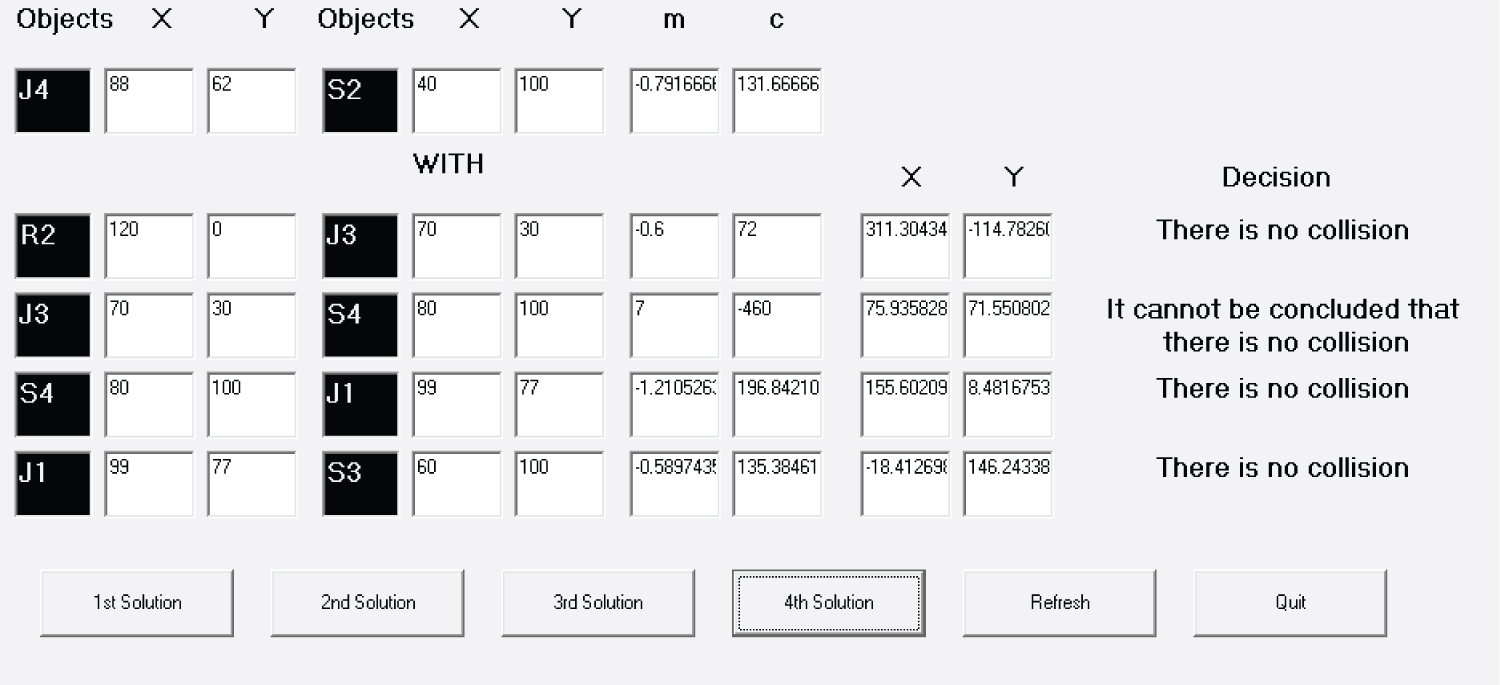
From Figure 10, it is found that the line S1-J4 will intersect the line R2-J3 at the point (-951.43, 642.86) which does not lie between the points R2 and J3. So there is no collision.

The line S1-J4 will intersect the line J3-S4 at the point (75.56, 68.95) which lies between the points J3 and S4 and between the points S1 and J4. So it cannot be concluded that there is no collision.

Let M be the point of intersection of S1-J4 and J3-S4. Location of M is (75.56, 68.95) (from Figure 10).

Distance of M from S1 is $\sqrt{{(75.56-20)}^2+{(68.95-100)}^2}$

Robot1 reached S1 covering a distance of 105.46 units (from Figure 2). For reaching M, Robot1 has to cover 105.46 + 63.65 = 169.11 units of distance which is covered in 169.11/v units of time (v is taken as the velocity of robot1).

Distance of M from J3 is $\sqrt{{(75.56-70)}^2+{(68.95-30)}^2}$ = 39.35 units

Robot2 reached J3 covering a distance of 58.31 units (from Figure 2).

For reaching M, Robot 2 has to cover 58.31 + 39.55 = 97.66 units of distance which is covered in 97.66/v units of time (v is taken as the velocity of robot2).

As 97.66/v < 169.11/v, Robot2 passes through the point M much earlier than Robot1 and so there is no collision.

From Figure 10, it is found that the line S1-J4 will intersect the line S4-J1 at the point (131.44, 37.72) which does not lie within the points S1 and J4. So there is no collision.

The line S1-J4 will intersect the line J1-S3 at the point (782.93, -326.34) which does not lie within the points S1 and J4. So there is no collision.

From Figure 11, it is found that the line J4-S2 will intersect the line R2-J3 at the point (311.30, -114.78) which does not lie between the points R2 and J3. So there is no collision.

The line J4-S2 will intersect the line J3-S4 at the point (75.94, 71.55) which lies between the points J3 and S4 and between the points J4 and S2. So it cannot be concluded that there is no collision.

Let N be the point of intersection of J4-S2 and J3-S4. Location of N is (75.94, 71.55) (from Figure 11).

Distance of N from J4 is $\sqrt{{(75.94-88)}^2+{(71.55-62)}^2}$ = 15.38 units.

Robot1 reached J4 covering a distance of 183.36(from Figure 2).

For reaching N, Robot1 has to cover 183.36 + 15.38 = 198.74 units of distance which is covered in 198.74/v units of time (v is taken as the velocity of robot1).

Distance of N from J3 is $\sqrt{{(75.94-70)}^2+{(71.55-30)}^2}$ = 40.98 units.

Robot2 reached J3 covering a distance of 58.31(from Figure 2).

For reaching N, Robot2 has to cover 58.31 + 40.98 = 99.29 units of distance which is covered in 99.29/v units of time (v is taken as the velocity of robot2).

As 99.29/v < 198.74/v, Robot2 passes through the point N much earlier than Robot1 and so there is no collision.

From Figure 11, it is found that the line J4-S2 will intersect the line S4-J1 at the point (155.60, 8.48) which does not lie between the points J4 and S2. So there is no collision.

The line J4-S2 will intersect the line J1-S3 at the point (-18.41, 146.24) which does not lie between the points J4 and S2. So there is no collision.

Demonstration of the algorithm with test case 2

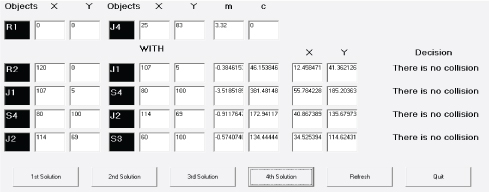
From Figure 12, it is found that the line R1-J4 intersects the line R2-J1 at the point (12.46, 41.36) which is not between the points R2 and J1. So there is no collision.

The line R1-J4 intersects the line J1-S4 at the point (55.78, 185.20) which is not between the points J1 and S4. So there is no collision.

The line R1-J4 intersects the line S4-J2 at the point (40.87, 135.68) which is not between the points S4 and J2. So there is no collision.

The line R1-J4 intersects the line J2-S3 at the point (34.53, 114.62) which is not between the points J2 and S3. So there is no collision.

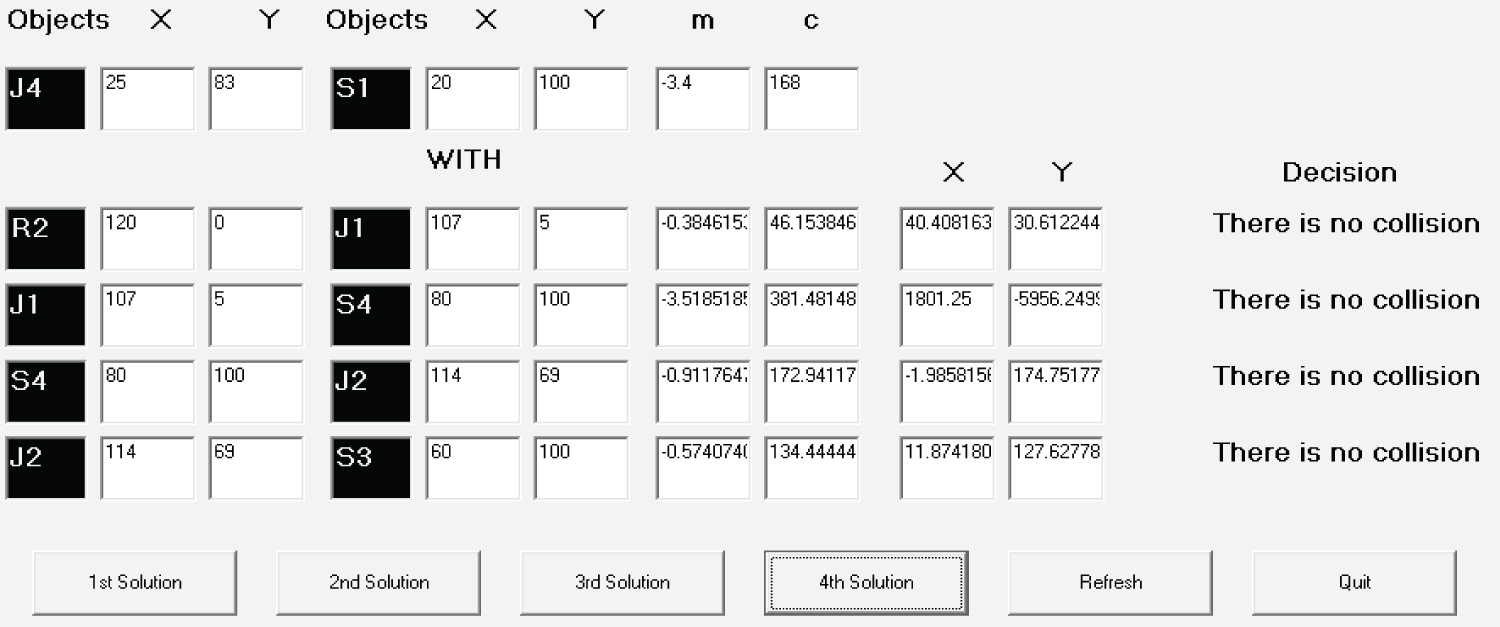
From Figure 13, it is found that the line J4-S1 intersects the line R2-J1 at the point (40.41, 30.61) which is not between the points R2 and J1. So there is no collision.

The line J4-S1 intersects the line J1-S4 at the point (1801.25, -5956.25) which is not between the points J1 and S4. So there is no collision.

The line J4-S1 intersects the line S4-J2 at the point (-1.99, 174.75) which is not between the points S4 and J2. So there is no collision.

The line J4-S1 intersects the line J2-S3 at the point (11.87, 127.63) which is not between the points J2 and S3. So there is no collision.

From Figure 14, it is found that the line S1-J3 intersects the line R2-J1 at the point (146.90, -10.34) which is not between the points R2 and J1. So there is no collision.

The line S1-J3 intersects the line J1-S4 at the point (99.70, 30.70) which is not between the points S1 and J3. So there is no collision.

The line S1-J3 intersects the line S4-J2 at the point (1316.36, -1027.27) which is not between the points S4 and J2. So there is no collision.

The line S1-J3 intersects the line J2-S3 at the point (-57.71, 167.57) which is not between the points J2 and S3. So there is no collision.

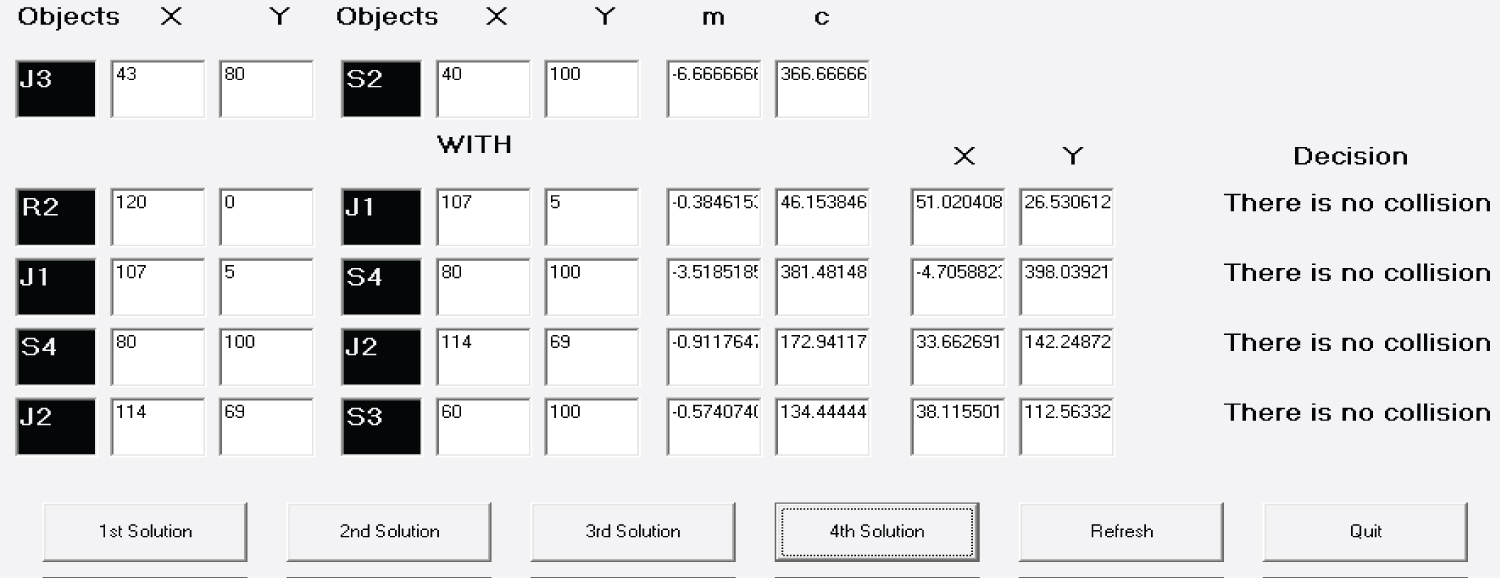
From Figure 15, it is found that the line J3-S2 intersects the line R2-J1 at the point (51.02, 26.53) which is not between the points R2 and J1. So there is no collision.

The line J3-S2 intersects the line J1-S4 at the point (-4.71, 398.04) which is not between the points J1 and S4. So there is no collision.

The line J3-S2 intersects the line S4-J2 at the point (33.66, 142.25) which is not between the points S4 and J2. So there is no collision.

The line J3-S2 intersects the line J2-S3 at the point (38.12, 112.56) which is not between the points J2 and S3. So there is no collision.

Demonstration of the algorithm with test case 3

From Figure 16, it is observed that the line R1-J4 intersects with the line R2-J2 at (91.79, 43.60) which is not between the points R1 and J4. So there is no collision.

The line R1-J4 intersects with the line J2-S4 at (71.76, 34.09) which is not between the points R1 and J4. So there is no collision.

The line R1-J4 intersects with the line S4-J1 at (-2400, -1140) which is not between the points R1 and J4. So there is no collision.

The line R1-J4 intersects with the line J1-S3 at (31.68, 15.05) which is not between the points J1 and S3. So there is no collision.

From Figure 17, it is observed that the line J4-S2 is a straight line parallel to the y-axis. So m could not be calculated. It intersects with the line R2-J2 at (40, 123.64) which is not between the points R2 and J2. So there is no collision.

The line J4-S2 intersects with the line J2-S4 at (40, -220) which is not between the points J2 and S4. So there is no collision.

The line J4-S2 intersects with the line S4-J1 at (40, 80) which is not between the points S4 and J1. So there is no collision.

The line J4-S2 intersects with the line J1-S3 at (40, 40) which is not between the points J1 and S3. So there is no collision.

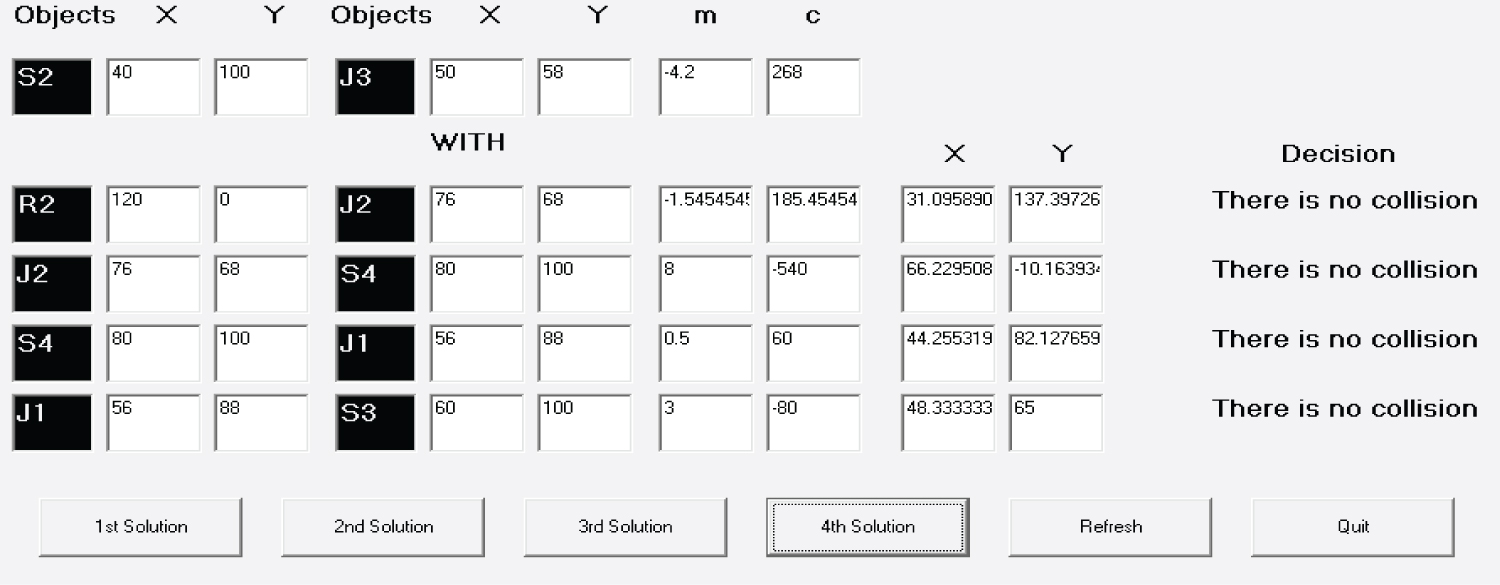
From Figure 18, it is observed that the line S2-J3 intersects with the line R2-J2 at (31.10, 137.40) which is not between the points R2 and J2. So there is no collision.

The line S2-J3 intersects with the line J2-S4 at (66.23, -10.16) which is not between the points J2 and S4. So there is no collision.

The line S2-J3 intersects with the line S4-J1 at (44.26, 82.13) which is not between the points S4 and J1. So there is no collision.

The line S2-J3 intersects with the line J1-S3 at (48.33, 65) which is not between the points J1 and S3. So there is no collision.

From Figure 19, it is observed that the line J3-S1 intersects with the line R2-J2 at (395, -425) which is not between the points R2 and J2. So there is no collision.

The line J3-S1 intersects with the line J2-S4 at (71.06, 28.51) which is not between the points J2 and S4. So there is no collision.

The line J3-S1 intersects with the line S4-J1 at (35.79, 77.89) which is not between the points S4 and J1. So there is no collision.

The line J3-S1 intersects with the line J1-S3 at (47.27, 61.82) which is not between the points J1 and S3. So there is no collision.

Conclusion

In this work, task planning for transportation of multiple objects by dual robots has been considered. A new algorithm has been developed for finding the routes for the robots in overall shortest possible time and another new algorithm has been developed to find out whether there is any collision between the two robots or not. As the robots are assumed to move with constant and same velocities, the distances covered by the robots are directly related to the time of movement of the robots. The algorithms have been implemented with different cases of object locations.

References

1. Pchelkin S, Shiriaev A, Robertsson A, et al. (2013) Integrated time-optimal trajectory planning and control design for industrial robot manipulator. IEEE/RSJ International Conference on Intelligent Robots and Systems.
2. Ata AA (2007) Optimal trajectory planning of manipulators: A review. Journal of Engineering Science and Technology. 1: 32.
3. Alatartsev S, Belov A, Nykolaychuk M, et al. (2014) Robot trajectory optimization for the relaxed end-effector path. Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics, 386-390.
4. LaValle S (2006) Planning algorithms. Cambridge University Press.
5. Applegate DL, Bixby RE, Chvatal V, et al. (2007) The traveling salesman problem: A computational study. Princeton University Press.
6. Kovacs A (2013) Task sequencing for remote laser welding in the automotive industry. In: 23rd International Conference on Automated Planning and Scheduling (ICAPS).
7. Zacharia P, Xidias E, Aspragathos N (2013) Task scheduling and motion planning for an industrial manipulator. Robotics and Computer-Integrated Manufacturing 29: 449-462.
8. Portugal D, Rocha R (2011) A survey on multi-robot patrolling algorithms. Technological Innovation for Sustainability, 139-146.
9. Wang L, Keshavarzmanesh S, Feng HY, et al. (2009) Assembly process planning and its future in Collaborative manufacturing: A review. The International Journal of Advanced Manufacturing Technology 41: 132-144.
10. Rego C, Gamboa D, Glover F, et al. (2011) Traveling salesman problem heuristics: Leading methods, implementations and latest advances. European Journal of Operational Research 211: 427-441.
11. Galceran E, Carreras M (2013) A survey on coverage path planning for robotics. Robotics and Autonomous Systems 61: 1258-1276.
12. Maimon O (1990) The robot task-sequencing planning problem. Robotics and Automation, IEEE Transactions, 760-765.
13. Zhang K, Collins EG, Shi D (2012) Centralized and distributed task allocation in multi-robot teams via a stochastic clustering auction. ACM Transactions on Autonomous and Adaptive Systems (TAAS) 7: 21.
14. Zhang K, Collins EG, Barbu A (2013) An efficient stochastic clustering auction for heterogeneous robotic collaborative teams. Journal of Intelligent & Robotic Systems 72: 541-558.
15. Cao T, Sanderson AC (1991) Task sequence planning in a robot workcell using and/or nets. Proceedings of the 1991 IEEE International Symposium on Intelligent Control, 239-244.
16. Chien SY, Xue LQ, Palakal M (1997) Task planning for a mobile robot in an indoor environment using object oriented domain information. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics 27: 1007-1016.
17. Chien Y, Hudli A, Palakal M (1998) Using many-sorted logic in the object-oriented data model for fast robot task planning. Journal of Intelligent and Robotic Systems 23: 1-25.
18. Galindo C, Fernandez-Madrigal JA, Gonzalez J (2004) Improving efficiency in mobile robot task planning through world abstraction. IEEE Transactions on Robotics 20: 677-690.
19. Bhatia A, Maly MR, Kavraki E, et al. (2011) Motion planning with complex goals. IEEE Robotics & Automation Magazine 18: 55-64.
20. Gaschler A, Petrick R, Giuliani M, et al. (2013) KVP: A knowledge of volumes approach to robot task planning. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 202-208.
21. Kuffner J (2010) Cloud-Enabled Robots. IEEE-RAS Int. Conf. on Hu-manoid Robots.
22. Inaba M (1997) Remote-brained robots. International Joint Conference on Artificial Intelligence, 1593-1606.
23. Kar A, Dutta AK, Debnath SK (2016) Task management of robot using cloud computing. IEEE International Conference on Computer, Electrical and Communication Engineering (ICCECE).
24. Kar A, Dutta AK, Debnath SK (2017) Task management of robot using priority job scheduling. International Journal of Computer Science and Information Technology 8: 260-265.
25. Kar A, Dutta AK, Debnath SK (2017) Optimising task management of robot and deciding whether cloud computing is feasible. IOSR Journal of Computer Engineering 19: 80-87.
26. Kar A, Dutta AK, Debnath SK (2018) Application of cloud computing for optimization of tasks by multiple robots operating in a co-operative environment. IEEE International Conference on Computer, Electrical and Communication Engineering (EECCMC).
27. Kar A, Dutta AK, Debnath SK (2018) Application of cloud computing for optimization of tasks scheduling by multiple robots operating in a co-operative environment. Springer International Conference on Intelligent Data Communication Technologies and Internet of Things (ICICI).
28. Kar A, Dutta AK, Debnath SK (2019) Application of cloud computing for optimization of tasks scheduling by multiple robots operating in a co-operative environment. Springer Series - Lecture Notes on Data Engineering and Communications Technologies book series (LNDECT) as Conference Proceedings of International Conference on Intelligent Data Communication Technologies and Internet of Things (ICICI) 26: 118-125.
29. Kar A, Dutta AK, Debnath SK (2018), Application of cloud computing for priority job scheduling by multiple robots operating in a co-operative environment. Springer 3rd International Conference on Recent Advancements in Computer Communication and Computational Sciences (ICRACCCS).
30. Kar A, Dutta AK, Debnath SK (2019) Application of cloud computing for priority job scheduling by multiple robots operating in a co-operative environment. Ambient communications and computer systems, Part of the Advances in Intelligent Systems and Computing book series (AISC) 904: 285-293.