Journal of Aerospace Engineering and Mechanics

Effects of Surface-Parallel Edge Restraints and Inter-laminar Shear on the Responses of Doubly Curved General Cross-Ply Panels

Abstract

This study presents first a relatively lesser studied topic of the role played by surface-parallel restraints in determining the response of simply supported thick to thin doubly curved cross-ply panels of rectangular plan-form, modeled using a third order shear deformation theory, quantified by way of the difference between full and absent surface-parallel edge restraints. Mathematically speaking, this corresponds to the difference between complementary solutions to mixed boundary-value problems, resulting from two extreme sets of surface-parallel restraints. Of special interest is the three-way interaction of the membrane action due to curvature with the surface-parallel boundary constraint as well as the higher-order (resp. first-order) bending-stretching coupling producing beam-column/tie-bar type softening/hardening effects in thick (respectively thin) asymmetric cross-ply panels. Comparison with other popular shear deformation theories, such as the layer-wise constant shear-angle theory or zig-zag theory and first order shear deformation theory, also constitutes an important focus of this investigation. Results for cross-ply plates are regenerated in order to show the severity of the effect of curvature, especially in the thin shell regime.

Keywords

Third order shear deformation theory (TSDT), Thick composite, Laminated panel, Asymmetric cross-ply, Doubly curved panel, Surface-Parallel boundary constraint, Mixed boundary-value problem, Boundary discontinuity, Double fourier series, Complementary solution, Bending-Stretching coupling, Beam-column effect, Tie-Bar effect, Membrane action, Inter-laminar shear deformation

Nomenclature

a, b = Dimensions of the plate parallel to the x₁ and x₂ axes, respectively.

h = Total thickness of a laminated curved panel.

m, n = Modal wave numbers in x₁ and x₂ directions, respectively.

N_i, M_i = Surface-parallel stress resultants and moment resultants, respectively (i = 1, 2, 6).

P_i = Third order moment resultants (i = 1, 2, 6).

Q_i, K_i = Transverse shear stress resultants and their third order counterparts, respectively (i = 1, 2).

Q = Distributed transverse load.

R_i = Principal radii of normal curvature of the reference (middle) surface in the x_i direction.

u_i = Components of displacement at the reference surface (x₁, x₂, 0) in x_i direction (i = 1, 2).

x_i = Orthogonal curvilinear coordinates.

φ_i = Rotation of the normal to the reference surface (i = 1, 2).

Introduction

Background Information

Curved panels (open shells), made of advanced laminated composite materials, e.g., carbon/epoxy, boron/epoxy, Kevlar/epoxy, carbon/PEEK, etc. are fast becoming common load-bearing structural elements in aerospace, hydrospace, ground transportation and many other civil/military applications, because of their possession of such beneficial properties as higher strength-to-weight ratios, longer (surface-parallel) fatigue (including sonic fatigue) life, better stealth characteristics, enhanced corrosion resistance, and so forth. Examples relating to recent aero-structural applications include but not limited to unmanned airborne vehicles (UAV), Boeing 787 Dreamliner (80% composites by volume, 50% by weight), Airbus A380 (composites more than 20% of airframe), F-22 Raptor (composites comprising 24% of the structural weight), F-35 JSF (Joint Strike Fighter, composites comprising 35% of airframe weight) among many others. Lesser known, but no less important are hydrospace applications in pressure hulls of submersibles [1-3], such as those used in search and rescue operations, e.g., in the Russian submarine, Kursk, disaster [4]. The composites used in such hydrospace applications must, by necessity, be thick-sectioned in order to avoid catastrophic collapse caused by structural buckling [5]. Additionally, since the transverse shear moduli, G_LT, G_TT, of a typical advanced polymeric composite material (transversely isotropic solid), such as carbon/epoxy, carbon/PEEK, etc. are known to be much lower than their longitudinal Young's modulus, E_L, which serves as a precursor for inter-laminar shear related fatigue failures. It follows that a reliable design/analysis of these critical structural components must incorporate higher order variation of inter-laminar shear stresses/strains into the formulation. Such pressure hulls must be made of curved panels of finite dimensions, necessitating solution to the boundary-value problem of a thick (highly shear-flexible) doubly curved panel, which entails, unlike either two centuries-old Navier's or close to a century-old Levy's approach, satisfaction of prescribed (admissible) boundary conditions at all four edges.

Typically, these laminated composite structures, subjected to thermo-mechanical loading, are analyzed using approximate numerical techniques or weak form of solutions, such as primarily finite element methods (FEM) [6-38], because of the ease with which problems, of nonlinearity, general plate/shell geometry, irregular shapes, non-uniform thickness, anisotropy, arbitrary lamination, complex boundaries involving multiple holes or cut-outs, general loading conditions and so on, can be handled by this method, but also more recently developed approximation methods, such as meshless Petrov-Galerkin methods [39,40], differential quadrature (DQ) method [41], radial basis function (RBF) method [42] and Sinc methods (especially in conjunction with boundary integral equation (BIE) methodology [43]. These weak or integral form of solutions are typically validated by comparing with their analytical (i.e., strong or differential form of solutions) counterparts, which are either exact (i.e., closed-form) or exact in the limit (e.g., Fourier series solutions), and which serve as bench-mark solutions for validation of approximate numerical solutions, such as those computed using the FEM. In principle, the above-mentioned variational or weighted residual type numerical procedures, such as the FEM, are known to be capable of satisfying the system of governing PDE's in some weak sense, and also the boundary limits (traces) of the solutions can be said to exist in some weak sense (trace theorem) and agree with the prescribed boundary data in some suitable function space, such as the Sobolev space, $\stackrel{0}{H_1}$, wherein the superscript ⁰ refers to the boundary. However, they fail to satisfy, in the point-wise sense ($C^{\infty }$), all the boundary conditions, especially the natural boundary constraints, and produced averaged out results across boundary discontinuities of unknown functions and/or their partial derivatives.

A number of semi-analytical methods have also appeared in the literature during the last two to three decades, the most noteworthy among them being the nonlinear resonance method, which is employed to compute elastic collapse pressures of shell-type structures weakened by modal imperfections [44-46]. Additionally, FEM-based semi-analytical post-processing approaches have also proven to be quite useful in enhancing the accuracy of inter-laminar shear stresses a posteriori [47-51]. While the equilibrium methods are reasonably accurate for symmetric laminates [47-49], they are not so in case of asymmetric laminates, which call for employment of the equilibrium/compatibility methods [50,51]. Li [52] has recently provided a fairly comprehensive review on layer-wise theories of laminated composite structures and their applications, covering majority of the topics discussed above.

Analytical or strong form of solutions

The present solution methodology is based on the double Fourier series approach. The primary mathematical issue at stake is whether "the hypothetical representation by Fourier series" possess "sufficient generality to satisfy all the required conditions and furnish a solution" [53]. In other words, existence of the resulting Fourier series solution is not guaranteed in the absence of additional appropriate mathematical "structures" to the formulation through introduction of certain boundary constraints [53,54]. This said, such hypothetical representation by double Fourier series can serve as particular solutions to plate/shell boundary-value problems under consideration. This step is followed by derivation of appropriate partial derivatives accounting for boundary discontinuities, of these functions and their partial derivatives, known as complementary boundary constraints (see Chaudhuri [54,55]. This step introduces boundary Fourier coefficients, which supply the complementary solution to the boundary-value problem. It must be emphasized here that "the complementary boundary constraints, which are inequalities, play as important a role as the (prescribed) admissible boundary conditions, which are equalities" [55]. Double Fourier series solutions to classical lamination theory (CLT)-based homogeneous and laminated plate and shell boundary value problems are available in Refs. [56-62] and [63-67], respectively. Likewise, double Fourier series based solutions to various first order shear deformation theory (FSDT)-based laminated anisotropic plate and shell boundary-value problems have been presented in Refs. [68-76] and [77-84], respectively.

Recent decades have, following the pioneering lead by Basset [85], witnessed the introduction of second- and third-order shear deformation theories (TSDT), entailing continuity of quadratic and cubic, respectively, distribution, of the surface-parallel (in-plane for flat panels) displacement components through the laminate thickness [19], see for detailed reviews by Reddy [19], and Chaudhuri and Kabir [86] for the decades prior to 2000, and Giunta, et al. [87], and Chaudhuri and Oktem [88,89], thereafter.

It is important to note here that an overwhelming majority of laminated plate/shell problems, formulated through employment of various higher-order shear deformation theories, are solved using the Navier type approach [19,90,91], only followed by that due to Levy [19,92-98] . It has been noted earlier that for cross-ply laminates, while the former can only produce particular solutions for very specific set of boundary constraints [88], i.e. the SS3 prescribed at all four edges, the latter essentially solves a curved or straight beam type of boundary-value problems, because of the SS3 being prescribed at the remaining two opposite edges; see Appendix A for definition of various boundary constraints.Oktem and co-workers [88-89,99-105] presented boundary-discontinuous type double Fourier series solutions of highly coupled system of partial differential equations (relating to cross-ply laminated plates/shells) subjected to various boundary conditions. Needless to state, Navier [19,90,91] and Levy-type solutions [19,92-98] to thick cross-ply flat and curved panels serve as special cases of the above.

Several researchers, e.g., [62,106-108], have published their experimental findings that endeavored to verify analytical predictions, such as mentioned above. More detailed reviews on this topic are available elsewhere [88], and will not be repeated here in the interest of brevity of presentation.

Motivation and Objective

This paper presents boundary-discontinuous double Fourier series solution to a class of self-adjoint differential system of five highly coupled fourth order linear partial differential equations, arising out of the afore-mentioned TSDT-based formulation for general cross-ply doubly curved panels, subjected to SS4 boundary conditions (full surface-parallel edge restraints). Novel numerical results are presented to understand the complex deformation behavior of simply supported (SS4) antisymmetric cross-ply panels with the membrane action due to the curvature effect. Although similar interaction of the in-plane edge restraint with the bending-stretching coupling has already been investigated in detail [100], the intricacies of the three-way interaction of the SS4 type simply supported boundary condition, which entails full surface-parallel boundary constraints, with the effect of curvature as well as the bending-stretching coupling, arising out of the asymmetry of lamination, has so far remained an enigma in the literature. Interaction of the membrane action due to curvature with the higher-order (respectively, first-order) bending-stretching coupling in thick (respectively, thin) cross-ply panels constitutes an important focus of this investigation.

The significance of four different types of simply supported boundary constraints is well-known in structural mechanics literature [109]. While the SS1 boundary constraint is a two-dimensional (mathematical model) extension of the roller type simple support of a beam, the SS4 can be considered to be a similar extension of the hinge type simple support of beam-like (e.g., bridge) structures. The single most important factor to the commercial and military aircraft and rocket motor case designers alike is, of course, the design flexibility inherent in these composite laminates, known as tailoring, which is essentially exploiting the possibility of obtaining optimum design through a combination of structural/material concepts, such as stacking sequence, choice of the component phases, etc., panel-edge restraints (or lack thereof) to meet specific design requirements. In the context of simply supported panel edge constraints, the responses of panels with the SS1 and the SS4 boundary conditions represent the two bounds, and the rest (i.e., SS2 or SS3) lies somewhere in between.

Of special interest here is the role played by surface-parallel restraints in determining the response of simply supported thick to thin doubly curved cross-ply panels of rectangular plan-form, quantified by way of the difference between full (SS4) and absent (SS1) surface-parallel edge restraints. Mathematically speaking, this corresponds to the difference between complementary solutions, to mixed boundary-value problems, resulting from two extreme sets of surface-parallel restraints, namely SS1 and SS4. Results for cross-ply plates are regenerated in order to show the severity of the effect of curvature, especially in the thin shell regime [100]. Finally, comparison with other popular shear deformation theories, such as the layer-wise constant shear-angle theory (LCST) or zig-zag theory, e.g., [30,110-114] and FSDT [72-115], also constitutes an important focus of the present investigation. It may be noted that Oktem and Chaudhuri [101] have shown that the elastic responses of the present TSDT-based cross-ply spherical panels are in qualitative agreement with their zig-zag or LCST (layer-wise constant shear angle theory)-based counterparts, computed using finite element methods (FEM) [113].

Outline

Section 2 presents the statement of the problem under investigation, while some of the details thereof are described in Appendix A, Appendix B and Appendix C. Specifically, the Euler-Lagrange equations representing the equations of equilibrium, and the associated admissible boundary constraints for the present TSDT, both derived using the principle of virtual work, are presented in Appendix A. Appendix B shows some of the constants that appear in the equations, while the classification of four different types of simply supported or clamped boundary constraints for the present TSDT, obtained from Appendix A, is presented in Appendix C. Section 3 supplemented by Appendix D presents the implementation of the boundary-continuous double Fourier series to analytically (exact in the limit) the boundary-value problem stated above. In Section 4, novel numerical results are presented to understand the complex deformation behavior of simply supported (SS4) antisymmetric doubly curved cross-ply panels. The intricacies of the interaction of the SS4 type simply supported boundary condition, which entails full surface-parallel boundary constraints, with the effect of curvature (membrane action) have so far remained largely unaddressed in the literature. Interaction of the membrane action due to the curvature effect with the third order (respectively, first-order) bending-stretching coupling producing beam-column/tie-bar type softening/hardening effects in thick (respectively, thin) cross-ply panels also constitutes an important focus of this investigation. Some interesting conclusions drawn from the present investigation are presented in Sub-Sec. 5, In addition, extensive suggestions for future research of laminated shells are provided in Section 6.

Statement of the Problem

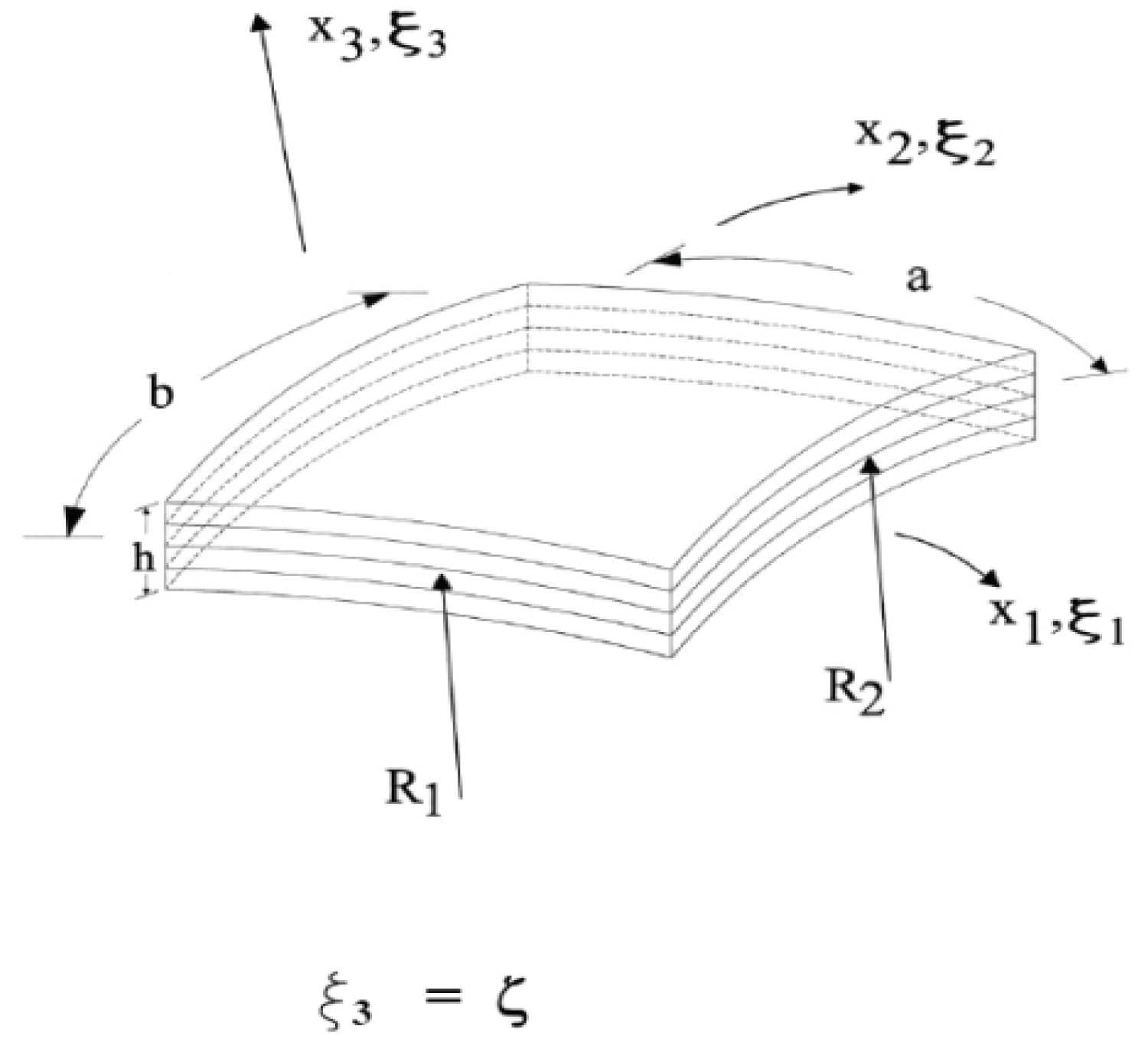
Figure 1 depicts a laminated doubly curved panel of rectangular planform, of length a, width b and thickness h. The cross-ply shell under consideration is composed of a finite number of orthotropic layers of uniform thickness. Strain-displacement relations from the theory of elasticity in curvilinear coordinates are given by [9]:

${\epsilon }_1({\xi }_1,{\xi }_2,{\xi }_3)=\frac{1}{(1+\frac{{\xi }_3}{R_1})g_1}\left[{\overline{u}}_{1,1}+\frac{1}{g_2}{g}_{1,2}{\overline{u}}_2+\frac{g_1}{R_1}{\overline{u}}_3\right]\text{ (1a)}$

${\epsilon }_2({\xi }_1,{\xi }_2,{\xi }_3)=\frac{1}{(1+\frac{{\xi }_3}{R_2})g_2}\left[{\overline{u}}_{2,2}+\frac{1}{g_1}{g}_{2,1}{\overline{u}}_1+\frac{g_2}{R_2}{\overline{u}}_3\right]\text{ (1b)}$

${\epsilon }_3({\xi }_1,{\xi }_2,{\xi }_3)={\overline{u}}_{3,3}\text{ (1c)}$

$${\epsilon }_5({\xi }_1,{\xi }_2,{\xi }_3)=\frac{1}{(1+\frac{{\xi }_3}{R_1})g_1}\left[{\overline{u}}_{3,1}-\frac{g_1}{R_1}{\overline{u}}_1\right]+{\overline{u}}_{1,3}\text{ (1d)}$$

${\epsilon }_5({\xi }_1,{\xi }_2,{\xi }_3)=\frac{1}{(1+\frac{{\xi }_3}{R_2})g_2}\left[{\overline{u}}_{3,2}-\frac{g_2}{R_2}{\overline{u}}_2\right]+{\overline{u}}_{2,3}\text{ (1e)}$

${\epsilon }_6({\xi }_1,{\xi }_2,{\xi }_3)=\frac{1}{(1+\frac{{\xi }_3}{R_1})g_1}\left[{\overline{u}}_{2,1}-\frac{1}{g_2}{g}_{1,2}{\overline{u}}_1\right]+\frac{1}{(1+\frac{{\xi }_3}{R_2})g_2}\left[{\overline{u}}_{1,2}-\frac{1}{g_2}{g}_{1,2}{\overline{u}}_1\right],\text{ (1f)}$

in which [114]

$g_{\lambda }=\frac{1}{{\left(\frac{1}{R_{G\lambda }^2}+\frac{1}{R_{\lambda }^2}\right)}^{1/2}},\begin{array}{cc}& \lambda =1,2\end{array}\text{ (2)}$

In Eq. (1), ${\epsilon }_i(i=1,2,3,4,5,6)$ represents the components of the strain tensor, and ${\overline{u}}_i$ (i = 1, 2, 3) denotes the components of the displacement vector along the (ε₁, ε₂, ε₃ = ζ) coordinates at a point, $({\xi }_1,{\xi }_2,{\xi }_3=\zeta )$. The principal radii of normal curvature of the reference (middle) surface are denoted by R₁ and R₂, while R_G1 and R_G2 represent the geodesic curvatures of ε₁ and ε₂ curves, respectively [114]. In order to model the kinematic behavior of the shell, an additional set of simplifying assumptions are invoked: (i) Transverse inextensibility, (ii) Moderate shallowness (in regards to the normal curvatures), and (iii) Negligibility of geodesic curvature. The last two assumptions permit the use of curved panel coordinates x₁, x₂, x₃= ζ, attached to the panel mid-surface. It may be noted that for a cylindrical shell, the lines of principal curvature coincide with the surface-parallel coordinate lines, while for a spherical or hyperbolic-paraboloidal shell, the same can be assumed upon negligence of the geodesic curvatures of the coordinate lines.

The surface-parallel displacements can be expanded in power series of ε₃ = ζ as suggested by Basset [85]. Only keeping the cubic terms and satisfying the conditions of transverse shear stresses (and hence strains) vanishing at a point (ε₁ε₂±h/2) on the outer (top) and inner (bottom) surfaces of the shell, yields [19,86,96]

${\overline{u}}_1=(1+\frac{\zeta }{R_1})u_1+\zeta {\phi }_1-\frac{4{\zeta }^3}{3h^2}({\phi }_1+\frac{1}{g_1}{u}_{3,1}),\text{ (3a)}$

${\overline{u}}_2=(1+\frac{\zeta }{R_2})u_2+\zeta {\phi }_2-\frac{4{\zeta }^3}{3h^2}({\phi }_2+\frac{1}{g_2}{u}_{3,2}),\text{ (3b)}$

${\overline{u}}_3=u_3\text{ (3c)}$

where $u_i(i=1,2,3)$ denotes the displacements of a point on the middle surface, while ${\phi }_1$ and ${\phi }_2$ are the rotations at ζ = 0 with respect to the ε₂ and ε₁ axes, respectively. The corresponding kinematic relations are given by

${\epsilon }_1={\epsilon }_1{}^0+\zeta ({\kappa }_1^0+{\zeta }^2{\kappa }_1^2),\text{ (4a)}$

${\epsilon }_2={\epsilon }_2{}^0+\zeta ({\kappa }_2^0+{\zeta }^2{\kappa }_2^2),\text{ (4b)}$

${\epsilon }_4={\epsilon }_4{}^0+{\zeta }^2{\kappa }_4^1,\text{ (4c)}$

${\epsilon }_5={\epsilon }_5{}^0+{\zeta }^2{\kappa }_5^1,\text{ (4d)}$

${\epsilon }_6={\epsilon }_6{}^0+\zeta ({\kappa }_6^0+{\zeta }^2{\kappa }_6^2),\text{ (4e)}$

in which

${\epsilon }_1{}^0=u_{1,1}+\frac{u_3}{R_1},{\kappa }_1^0={\phi }_{1,1},{\kappa }_1^2=-\frac{4}{3h^2}({\phi }_{1,1}+u_{3,11})\text{ (5a-c)}$

${\epsilon }_2{}^0=u_{2,2}+\frac{u_3}{R_2},{\kappa }_2^0={\phi }_{2,2},{\kappa }_2^2=-\frac{4}{3h^2}({\phi }_{2,2}+u_{3,22})\text{ (5d-f)}$

${\epsilon }_4{}^0=u_{3,2}+{\phi }_2,{\kappa }_4^1=-\frac{4}{h^2}({\phi }_2+u_{3,2})\text{ (5g,h)}$

${\epsilon }_5{}^0=u_{3,1}+{\phi }_1,{\kappa }_5^1=-\frac{4}{h^2}({\phi }_1+u_{3,1})\text{ (5i,j)}$

${\epsilon }_6{}^0=u_{2,1}+u_{1,2},{\kappa }_6^0={\phi }_{2,1}+{\phi }_{1,2},{\kappa }_6^2=-\frac{4}{3h^2}({\phi }_{2,1}+{\phi }_{1,2}+2u_{3,12})\text{ (5k-m)}$

For a general cross-ply (symmetric ${[0^0/{90}^0\mathrm{.....}]}_S$ and antisymmetric $[0^0/{90}^0/0^0/{90}^0\mathrm{.....}]$ being two special cases) shell, the following elastic rigidities (integrated stiffnesses), given by Eqs. (A6) in the Appendix A, are zero:

$\begin{array}{l}{A}_{16}=A_{26}=B_{12}=B_{16}=B_{26}=D_{16}=D_{26}=D_{45}=A_{45}=E_{12}\text{ (6)}\\ =E_{16}=E_{26}=F_{16}=F_{26}=F_{45}=H_{16}=H_{26}=0\end{array}$

The stress resultants, moment resultants and higher-order moment and shear resultants, given by Eqs. (A5) in terms of components of displacement and rotation, can now be written as follows:

$N_1=A_{11}{u}_{1,1}+a_1{u}_3+A_{12}{u}_{2,2}+a_2{\phi }_{1,1}+a_3{\phi }_{2,2}-a_4{u}_{3,11}-a_5{u}_{3,22},\text{ (7a)}$

$N_2=A_{12}{u}_{1,1}+a_6{u}_3+A_{22}{u}_{2,2}+a_3{\phi }_{1,1}+a_7{\phi }_{2,2}-a_5{u}_{3,11}-a_8{u}_{3,22},\text{ (7b)}$

$N_6=A_{66}{u}_{2,1}+A_{66}{u}_{1,2}+a_9{\phi }_{2,1}+a_9{\phi }_{1,2}-a_{10}{u}_{3,12},\text{ (7c)}$

$$M_1=B_{11}{u}_{1,1}+b_1{u}_3+B_{12}{u}_{2,2}+b_2{\phi }_{1,1}+b_3{\phi }_{2,2}-b_4{u}_{3,11}-b_5{u}_{3,22},\text{ (7d)}$$

$$M_2=B_{12}{u}_{1,1}+b_6{u}_3+B_{22}{u}_{2,2}+b_3{\phi }_{1,1}+b_7{\phi }_{2,2}-b_5{u}_{3,11}-b_8{u}_{3,22},\text{ (7e)}$$

$$M_6=B_{66}{u}_{2,1}+B_{66}{u}_{1,2}+b_9{\phi }_{2,1}+b_9{\phi }_{1,2}-b_{10}{u}_{3,12},\text{ (7f)}$$

$$P_1=E_{11}{u}_{1,1}+b_{11}{u}_3+E_{12}{u}_{2,2}+b_{12}{\phi }_{1,1}+b_{13}{\phi }_{2,2}-b_{14}{u}_{3,11}-b_{15}{u}_{3,22},\text{ (7g)}$$

$$P_2=E_{12}{u}_{1,1}+b_{19}{u}_3+E_{22}{u}_{2,2}+b_{13}{\phi }_{1,1}+b_{16}{\phi }_{2,2}-b_{15}{u}_{3,11}-b_{17}{u}_{3,22},\text{ (7h)}$$

$$P_6=E_{66}{u}_{2,1}+E_{66}{u}_{1,2}+b_{18}{\phi }_{2,1}+b_{18}{\phi }_{1,2}-b_{19}{u}_{3,12},\text{ (7i)}$$

$Q_2=d_1{\phi }_2+d_1{u}_{3,2},\text{ (7j,k)}$

$K_1=d_4{\phi }_1+d_4{u}_{3,1},K_2=d_3{\phi }_2+d_3{u}_{3,2}.\text{ (7l,m)}$

The constants, $a_i,b_i,d_i$, referred to Eqs. (6), are given in Appendix B.

Substitution of Eqs. (7) into equilibrium equations given by Eqs. (A3) supplies the following five highly coupled fourth-order governing partial differential equations [89,96].

$$A_{11}{u}_{1,11}+a_1{u}_{3,1}+f_1{u}_{2,12}+a_2{\phi }_{1,11}+f_2{\phi }_{2,12}-a_4{u}_{3,111}+f_3{u}_{3,122}+A_{66}{u}_{1,22}+a_9{\phi }_{1,22}=0,\text{ (8a)}$$

$$A_{66}{u}_{2,11}+f_1{u}_{1,12}+a_9{\phi }_{2,11}+f_2{\phi }_{1,12}+f_3{u}_{3,112}+A_{22}{u}_{2,22}+a_6{u}_{3,2}+a_7{\phi }_{2,22}-a_8{u}_{3,222}=0\text{ (8b)}$$

$$\begin{array}{l}{f}_4{\phi }_{1,1}+f_5{\phi }_{2,2}+f_6{u}_{3,11}+f_7{u}_{3,22}+a_4{u}_{1,111}+f_8{u}_{2,112}+\text{ (8c)}\\ f_9{\phi }_{1,111}+f_{10}{\phi }_{2,112}-f_{11}{u}_{3,1111}\\ +f_{12}{u}_{3,1122}+f_8{u}_{1,122}+a_8{u}_{2,222}+f_{10}{\phi }_{1,122}+f_{13}{\phi }_{2,222}-\\ f_{14}{u}_{3,2222}-a_1{u}_{1,1}-a_6{u}_{2,2}+f_{15}{u}_3=-q\end{array}$$

$$\begin{array}{l}{a}_2{u}_{1,11}+e_1{u}_{2,12}+e_2{u}_{3,1}+e_3{\phi }_{1,11}+e_4{\phi }_{2,12}+\text{ (8d)}\\ e_5{\phi }_{1,22}+e_6{u}_{3,111}+e_7{u}_{3,122}+a_9{u}_{1,22}+e_8{\phi }_1=0\end{array}$$

$$\begin{array}{l}{a}_9{u}_{2,11}+e_1{u}_{1,12}+e_5{\phi }_{2,11}+e_4{\phi }_{1,12}+e_7{u}_{3,112}+\text{ (8e)}\\ a_7{u}_{2,22}+e_{12}{u}_{3,2}+e_9{\phi }_{2,22}+e_{10}{u}_{3,222}+e_{11}{\phi }_2=0\end{array}$$

where $a_i,e_i$ and $f_i$ are constants, which are given in Appendix B.

In what follows, the above system of five partial differential equations is solved in conjunction with the SS4 type simply supported boundary condition, prescribed at the edges, $x_1=0,a$, and $x_2=0,b$, which are given as follows:

SS4 type simply supported boundary condition, prescribed at the edges, $x_1=0,a$ and $x_2=0,b$ which are given as follows (Refer to Figure 19d, and Eqs. (C1) and (C2d) in Appendix C):

$$u_3(0,x_2)=u_3(a,x_2)=u_3(x_1,0)=u_3(x_1,b)=0\text{ (9a)}$$

$${\phi }_2(0,x_2)={\phi }_2(a,x_2)={\phi }_1(x_1,0)={\phi }_1(x_1,b)=0\text{ (9b)}$$

$$u_1(0,x_2)=u_1(a,x_2)=u_1(x_1,0)=u_1(x_1,b)=0\text{ (9c)}$$

$$u_2(0,x_2)=u_2(a,x_2)=u_2(x_1,0)=u_2(x_1,b)=0\text{ (9d)}$$

$$M_1(0,x_2)=M_1(a,x_2)=M_2(x_1,0)=M_2(x_1,b)=0,\text{ (9e)}$$

$$P_1(0,x_2)=P_1(a,x_2)=P_2(x_1,0)=P_2(x_1,b)=0\text{ (9f)}$$

Solution Methodology

The solution methodology is based on the boundary discontinuous double Fourier series approach [54,55] to solve boundary value problems, involving partial differential equations (with constant coefficients) of arbitrary orders subjected to corresponding admissible boundary conditions, of plate/shell type structural components of rectangular planform, with the starting point of selecting particular solution functions. These are assumed as follows:

$$u_1\left(x_1,x_2\right)={\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=1}^{\infty }{U}_{mn}\cos (\alpha x_1)}}\sin (\beta x_2),x_1\in \left(0,a\right),x_2\in \left[0,b\right]\text{ (10a)}$$

$$u_2\left(x_1,x_2\right)={\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=0}^{\infty }{V}_{mn}\sin (\alpha x_1)}}\cos (\beta x_2),x_1\in \left[0,a\right]{,}_{}{x}_2\in \left(0,b\right)\text{ (10b)}$$

$$u_3\left(x_1,x_2\right)={\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }{W}_{mn}\sin (\alpha x_1)}}\sin (\beta x_2),x_1\in \left[0,a\right],x_2\in \left[0,b\right]\text{ (10c)}$$

$${\phi }_1\left(x_1,x_2\right)={\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=1}^{\infty }{X}_{mn}\cos (\alpha x_1)}}\sin (\beta x_2),x_1\in \left[0,a\right],x_2\in \left[0,b\right]\text{ (10d)}$$

$${\phi }_2\left(x_1,x_2\right)={\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=0}^{\infty }{Y}_{mn}\sin (\alpha x_1)}}\cos (\beta x_2)\text{ (10e)}$$

where, $\alpha =\frac{m\pi }{a},\beta =\frac{n\pi }{b}$ (11)

It may be noted that the assumed surface-parallel displacement functions for all edges SS4, while being identical to their SS1 counterparts [101], admit boundary discontinuities (complementary boundary constraints) different from the latter. The transverse displacement and the two rotations do not, as before, exhibit any boundary discontinuity, and are identical to their SS1 counterparts.

The total number of unknown Fourier coefficients introduced in Eqs. (10) enumerate to 5mn + 2m + 2n. The next operation is comprised of partial differentiation of the assumed particular solution functions. The procedure for differentiation of these functions is based on Lebesgue integration theory that introduces boundary Fourier coefficients arising from discontinuities, known as complementary boundary constraints [54,55], of the particular solution functions at the edges x₁ = 0, a, and x₁ = 0, b. As has been noted by Chaudhuri [55], the boundary Fourier coefficients serve as complementary solution to the problem under investigation. The procedure imposes certain boundary constraints in the form of equalities and complementary boundary constraints in the form of inequalities, the details of which are available in Chaudhuri [54,55], and will not be further discussed here in the interest of brevity of presentation. The partial derivatives, which cannot be obtained by term-wise differentiation, are obtained as follows. The above function u₁ and its first partial derivative, $u_{1,1}$ obtained by term-wise differentiation, are not satisfied at the edges, x₁ = 0, a, thus violating the boundary constraints and complementary boundary constraints, respectively, at these edges. Therefore, u1 is forced to vanish at these edges (boundary constraints), while for further differentiation, $u_{1,11}$ is expanded in double Fourier series, in the form suggested by Chaudhuri [54,55], in order to satisfy the complementary boundary constraint (inequality). The partial derivatives are then obtained as follows [55].

$$u_{1,1}=-{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\alpha U_{mn}\sin (\alpha x_1)\sin (\beta x_2)}},\text{ (12a)}$$

$$u_{1,11}=\frac{1}{2}{\displaystyle \sum _{m=1}^{\infty }{\overline{c}}_n}\sin (\beta x_2)+{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\left[-{\alpha }^2{U}_{mn}+{\gamma }_m{\overline{c}}_n+{\psi }_m{\overline{d}}_n\right]\cos (\alpha x_1)}}\sin (\beta x_2)\text{ (12b)}$$

In a manner similar to $u_1,u_2$, is forced to vanish at the edges, $x_2=0$ and b. The derivatives of $u_2$ are given as follows:

$$u_{2,2}=-{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\beta V_{mn}\sin (\alpha x_1)}}\sin (\beta x_2)\text{ (13a)}$$

$$u_{2,22}=\frac{1}{2}{\displaystyle \sum _{m=1}^{\infty }{\overline{a}}_m}\sin (\alpha x_1)+{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\left[-{\beta }^2{V}_{mn}+{\gamma }_n{\overline{a}}_m+{\psi }_n{\overline{b}}_m\right]\sin (\alpha x_1)}}\cos (\beta x_2)(13b)$$

in which

$$\left({\gamma }_n,{\psi }_n\right)=\left\{\begin{array}{c}\left(0,1\right),\begin{array}{cc}& n=odd,\end{array}\\ \left(1,0\right),\begin{array}{cc}& n=even,\end{array}\end{array}\right.\text{ (14)}$$

and the boundary Fourier coefficients ${\overline{a}}_m,{\overline{b}}_m,{\overline{c}}_n$ and ${\overline{d}}_n$ are defined in Appendix D. The remaining partial derivatives can be obtained by term-wise differentiation. The above step generates additional 2m + 2n (unknown) boundary Fourier coefficients.

Introduction of the displacement functions and their appropriate derivatives into the governing partial differential equations will supply the following 5mn + 2m + 2n equations:

$${\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\cos (\alpha x_1)\sin (\beta x_2)\left\{\begin{array}{l}\left(-{\alpha }^2{A}_{11}-{\beta }^2{A}_{66}\right)U_{mn}+\left(-\alpha \beta f_1\right)V_{mn}\\ +\left(a_2\alpha -f_3\alpha {\beta }^2+a_4{\alpha }^3\right)W_{mn}+\left(-a_9{\beta }^2-a_2{\alpha }^2\right)X_{mn}\\ +\left(-\alpha \beta f_2\right)Y_{mn}+A_{11}\left({\gamma }_m{\overline{c}}_n+{\psi }_m{\overline{d}}_n\right)\end{array}\right\}}}=0\text{ (15a)}$$

$${\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\sin (\alpha x_1)\cos (\beta x_2)\left\{\begin{array}{l}\left(-\alpha \beta f_1\right)U_{mn}+\left(-A_{66}{\alpha }^2-A_{22}{\beta }^2\right)V_{mn}\\ +\left(a_6\beta -f_3{\alpha }^2\beta +a_8{\beta }^3\right)W_{mn}+\left(-f_2\alpha \beta \right)X_{mn}\\ +\left(-a_9{\alpha }^2-a_7{\beta }^2\right)Y_{mn}-A_{22}\left({\gamma }_n{\overline{a}}_m+{\psi }_n{\overline{b}}_m\right)\end{array}\right\}}}=0\text{ (15b)}$$

$$\begin{array}{l}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\sin (\alpha x_1)\sin (\beta x_2)\left\{\begin{array}{l}\left(a_1\alpha +a_4{\alpha }^3+f_8\alpha {\beta }^2\right)U_{mn}+\left(a_6\beta +a_8{\beta }^3+f_8{\alpha }^2\beta \right)V_{mn}\\ +\left(-f_6{\alpha }^2+f_{15}-f_7{\beta }^2-f_{11}{\alpha }^4+f_{12}{\alpha }^2{\beta }^2-f_{14}{\beta }^4\right)W_{mn}\\ +\left(-f_4\alpha +f_9{\alpha }^3+f_{10}\alpha {\beta }^2\right)X_{mn}+\left(-f_5\beta +b_{13}{\beta }^3+f_{10}{\alpha }^2\beta \right)Y_{mn}\\ -a_4\alpha \left({\gamma }_m{\overline{c}}_n+{\psi }_m{\overline{d}}_n\right)-a_8\beta \left({\gamma }_n{\overline{a}}_m+{\psi }_n{\overline{b}}_m\right)\end{array}\right\}}}\\ =-{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }{q}_{mn}}}\sin (\alpha x_1)\sin (\beta x_2)\text{ (15c)}\end{array}$$

$$\begin{array}{l}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\cos (\alpha x_1)\sin (\beta x_2)\left\{\begin{array}{l}\left(-{\alpha }^2{a}_2-{\beta }^2{a}_9\right)U_{mn}+\left(-\alpha \beta e_1\right)V_{mn}\\ +\left(-e_6{\alpha }^3-e_7\alpha {\beta }^2+e_2\alpha \right)W_{mn}+\left(e_8-e_3{\alpha }^2-e_5{\beta }^2\right)X_{mn}\\ +\left(-e_4\alpha \beta \right)Y_{mn}+a_2\left({\gamma }_m{\overline{c}}_n+{\psi }_m{\overline{d}}_n\right)\end{array}\right\}}}\\ =0\text{ (15d)}\end{array}$$

$$\begin{array}{l}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\sin (\alpha x_1)\cos (\beta x_2)\left\{\begin{array}{l}\left(-\alpha \beta e_1\right)U_{mn}+\left(-a_9{\alpha }^2-a_7{\beta }^2\right)V_{mn}\\ +\left(e_{12}\beta -e_7{\alpha }^2\beta -e_{10}{\beta }^3\right)W_{mn}+\left(-e_4\alpha \beta \right)X_{mn}\\ +\left(-e_5{\alpha }^2+e_{11}-e_9{\beta }^2\right)Y_{mn}+a_7\left({\gamma }_n{\overline{a}}_m+{\psi }_n{\overline{b}}_m\right)\end{array}\right\}}}\\ =0\text{ (15e)}\end{array}$$

$${\displaystyle \sum _{n=1}^{\infty }\sin (\beta x_2)\left\{-\frac{A_{66}}{2}{\beta }^2{U}_{0n}-a_9{\beta }^2{X}_{0n}+\frac{A_{11}}{2}{\overline{c}}_n\right\}}=0\text{ (16a)}$$

$${\displaystyle \sum _{m=1}^{\infty }\sin (\alpha x_1)\left\{-\frac{A_{66}}{2}{\alpha }^2{V}_{m0}-a_9{\alpha }^2{Y}_{m0}+\frac{A_{22}}{2}{\overline{a}}_m\right\}}=0\text{ (16b)}$$

$${\displaystyle \sum _{n=1}^{\infty }\sin (\beta x_2)\left\{-\frac{a_9}{2}{\beta }^2{U}_{0n}+\left(e_8-e_5{\beta }^2\right)X_{0n}+\frac{a_2}{2}{\overline{c}}_n\right\}}=0\text{ (16c)}$$

$${\displaystyle \sum _{m=1}^{\infty }\sin (\alpha x_1)\left\{-\frac{a_9}{2}{\alpha }^2{V}_{m0}+(e_{11}-e_5{\alpha }^2)Y_{m0}+\frac{a_7}{2}{\overline{a}}_m\right\}}=0\text{ (16d)}$$

Satisfying the geometric boundary conditions given by Eqs. (9c, d), i.e., those pertaining to vanishing of $u_1$ and $u_2$ at the appropriate edges, and equating the coefficients of $\sin (\alpha x_1),\cos (\beta x_2)$ etc. yield the following algebraic equations:

For all values of $n=1,2,\mathrm{........}$

1. ${\displaystyle \sum _{m=1,3,5,\mathrm{......}}^{\infty }{\psi }_m{U}_{mn}=0},U_{0n}+{\displaystyle \sum _{m=2,4,6,\mathrm{.......}}^{\infty }{\gamma }_m{U}_{mn}=0}\text{ (17a,b)}$

For all values of $m=1,2,\mathrm{........}$

2. ${\displaystyle \sum _{n=1,3,5,\mathrm{......}}^{\infty }{\psi }_n{V}_{mn}=0},V_{m0}+{\displaystyle \sum _{n=2,4,6,\mathrm{.......}}^{\infty }{\gamma }_n{V}_{mn}=0}\text{ (17c,d)}$

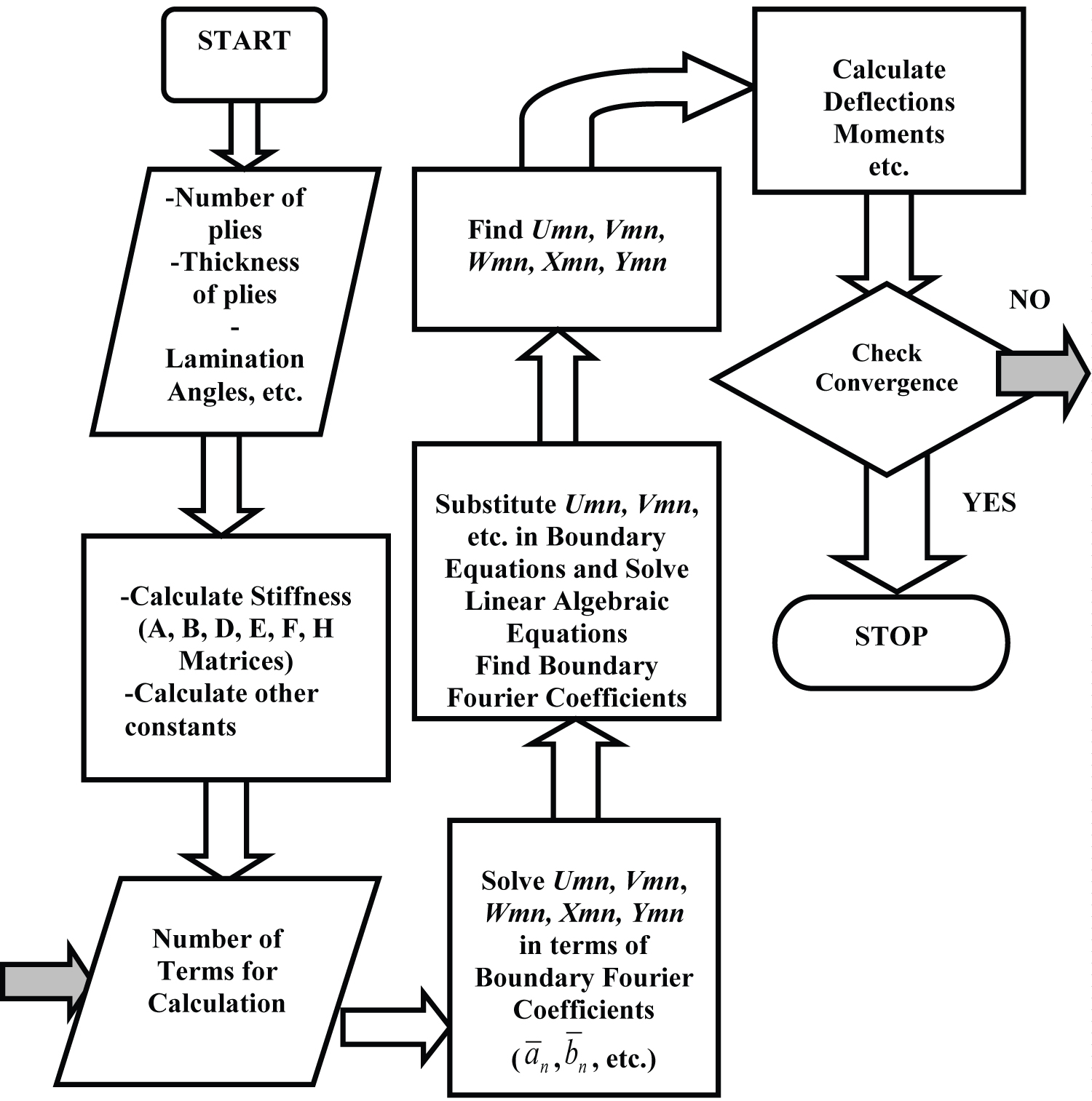
The geometric boundary conditions, given by Eqs. (9a), relating to $u_3$ are satisfied as a priori at the edges, x₁ = 0, a, and x₂= 0, b. Similarly, the rotations φ₁ and φ₂ also satisfy the boundary conditions, given by Eqs. (9b) a priori. The natural boundary conditions relating to M₁, M₂, P₁, and P₂ and given by Eqs, (9e,f) are also satisfied as a priori. This step generates additional 2m + 2n equations for the solution. Finally, the above operations result in, in total, 5mn + 4m + 4n linear equations in as many unknowns. In the interest of computational efficiency, Eqs. (15) are solved for $U_{mn},V_{mn},W_{mn},X_{mn},Y_{mn}$ , and Eqs. (16) for $U_{0n},X_{0n},V_{m0}$ and $Y_{m0}$, in terms of the unknown boundary Fourier coefficients ${\overline{a}}_m,{\overline{b}}_m,{\overline{c}}_n$ and ${\overline{d}}_n$, defined in Eqs. (D1a, b) below [89,96,100], in a manner outlined in Figure 2.

These Fourier coefficients are then substituted in natural boundary conditions, given by Eqs. (17), thus reducing the size of the matrix to be inverted by orders of magnitude (from a system of 5mn + 4m + 4n to that of 2m + 2n equations in as many unknowns) depending on the cut-off values of m and n. Resulting equations are finally solved for boundary Fourier coefficients ${\overline{a}}_m,{\overline{b}}_m,{\overline{c}}_n$ and, ${\overline{d}}_n$ using a MATLAB (version R2014b) code developed by the authors. When and vanish, the Navier type solution due to Reddy [19] is recovered.

Numerical Results and Discussions

In what follows, the numerical results are presented using the following material properties:

(a) Material type I: E₁ = 175.78 GPA (25,000 Ksi); E₁/E₂ = 25; G₁₂/E₂ = G₁₃/E₂ = 0.5; G₂₃/E₂ = 0.2; ν₁₂ = 0.25,

(b) Material type II: E₁ = 105.47 GPA (15,000 Ksi); E₁/E₂ = 15; G₁₂/E₂ = G₁₃/E₂ = 0.4286; G₂₃/E₂ = 0.3429;

ν₁₂ = 0.40,

(c) Material type III: E₁ = 175.78 GPA (25,000 Ksi); E₁/E₂ = 25; G₁₂/E₂ = G₁₃/E₂ = G₂₃/E₂ = 0.5; ν₁₂ = 0.25,

Where Ei, i = 1, 2, denotes the surface-parallel Young's modulus in x_i, i = 1, 2, coordinate direction. G₁₂ and ν₁₂ represent the surface-parallel shear modulus and major Poisson's ratio, respectively, on the x₁-x₂ surface, while G₁₃ and G₂₃ are transverse shear moduli in the x₁-x₂and x₂-x₂planes, respectively. It may be remarked that the shear moduli display nonlinear characteristics [109,116]. An expression for the nonlinear shear modulus, G₁₂ (=G₁₃) is derived, by Chaudhuri [116] based on the assumption of uniform distribution of micro-kinks and fiber misalignment defects. Fiber micro-kinking is caused by crystallite disorientations, as detected by the Raman [117] and X-Ray measurements, inside a carbon fiber. This said, this type of material nonlinearity can be ignored for small deflection analysis of polymer matrix composite (PMC) structural elements without much loss of accuracy (in the interest of analytical convenience). However, material nonlinearity must be accounted for analysis of metal matrix composite (MMC) structural elements, e.g., boron/aluminum tubes [118]. The following normalized quantities are defined:

$$u_3^{*}=\frac{{10}^3{E}_2{h}^3}{q_0{a}^4}{u}_3,M_1^{*}=\frac{{10}^3}{q_0{a}^2}{M}_1,$$

in which 'a' is assumed equal to 812.8 mm (32 in.) q0 denotes the uniformly distributed transverse load. For all the numerical results presented in all figures except the Figure 12 the displacement u3, and moment M1, are computed at the center of the panel.

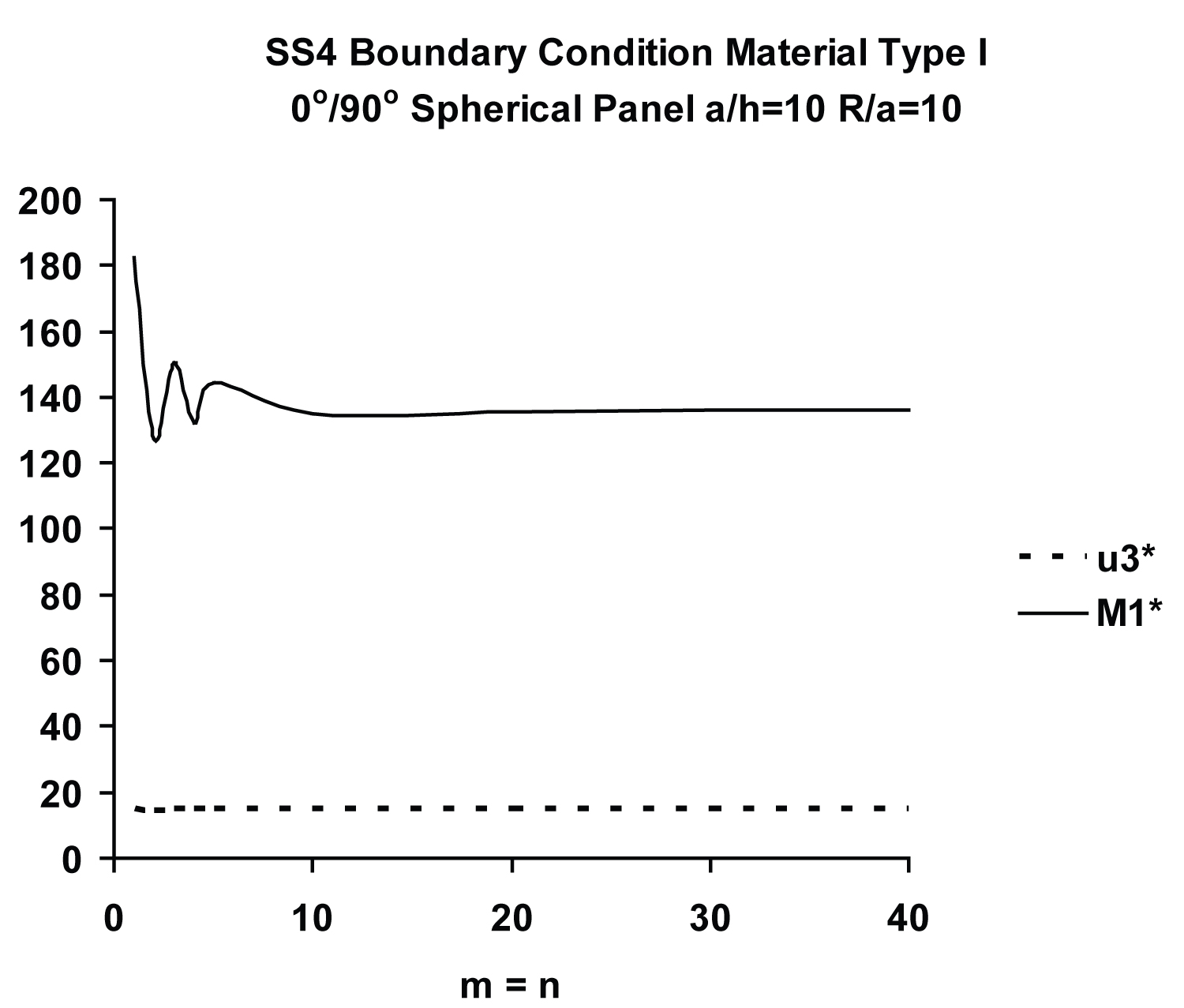
The convergence (with m = n) of normalized transverse displacement (deflection), u₃^* and moment, M₁^*, of a moderately thick (a/h = 10) antisymmetric cross-ply [0°/90°] square shell, computed using the present TSDT with the material type I for SS4 type boundary condition is displayed in Figure 3. Unlike its SS1 counterpart (see Figure 2 of Oktem and Chaudhuri [101], the convergence plot of the central moment, $M_1^{*}$, exhibits an initially oscillatory behavior; the oscillations, however, die down very rapidly, rendering the convergence plot practically monotonic for m, n ≥ 10. The reason can be attributed to the additional discontinuities on the boundaries introduced by the SS4 boundary condition [100]. The convergence rate decreases when there are more discontinuities in the problem, which is a well-known fact in Fourier series analysis.

Effects of Edge restraints and curvature

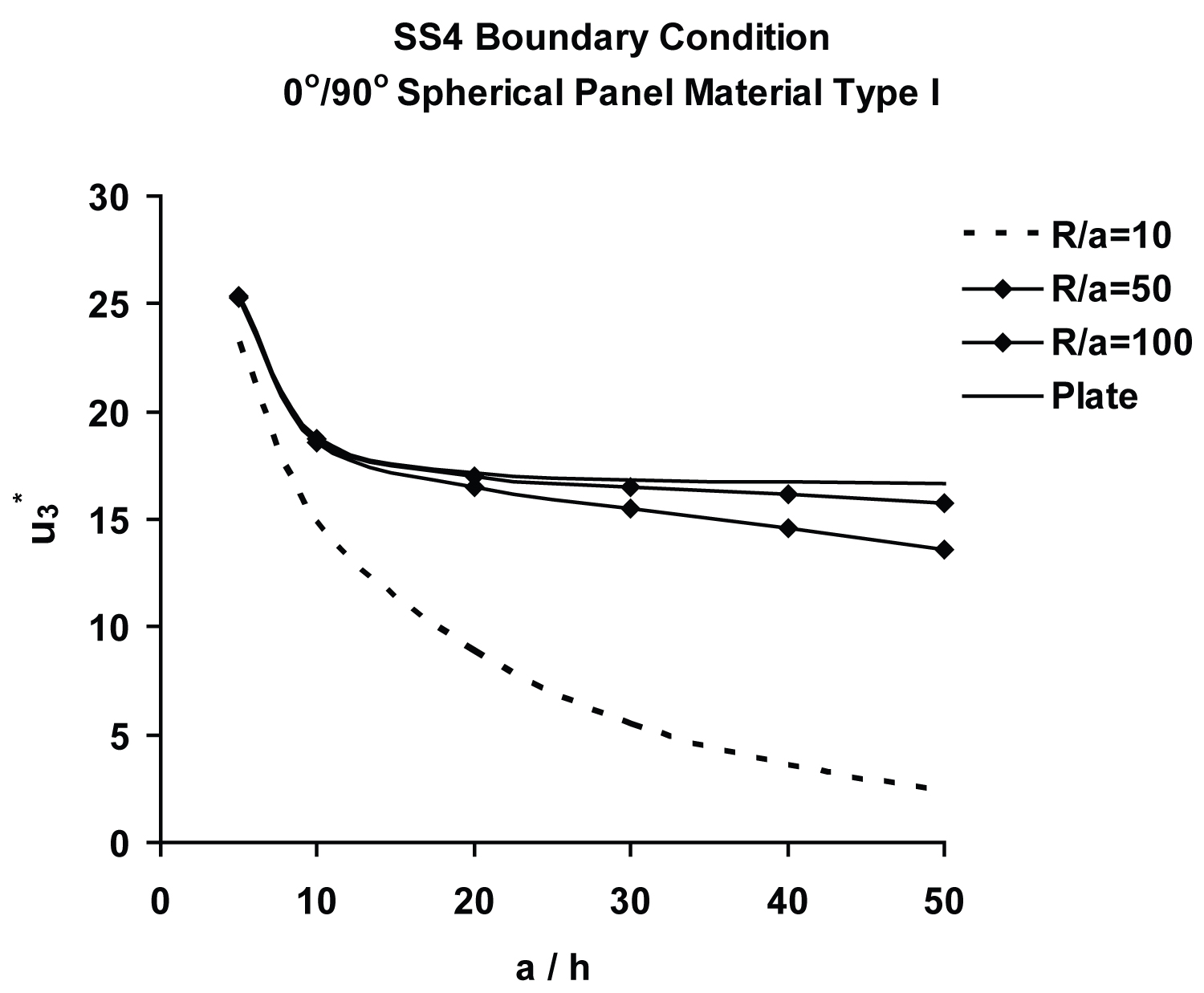
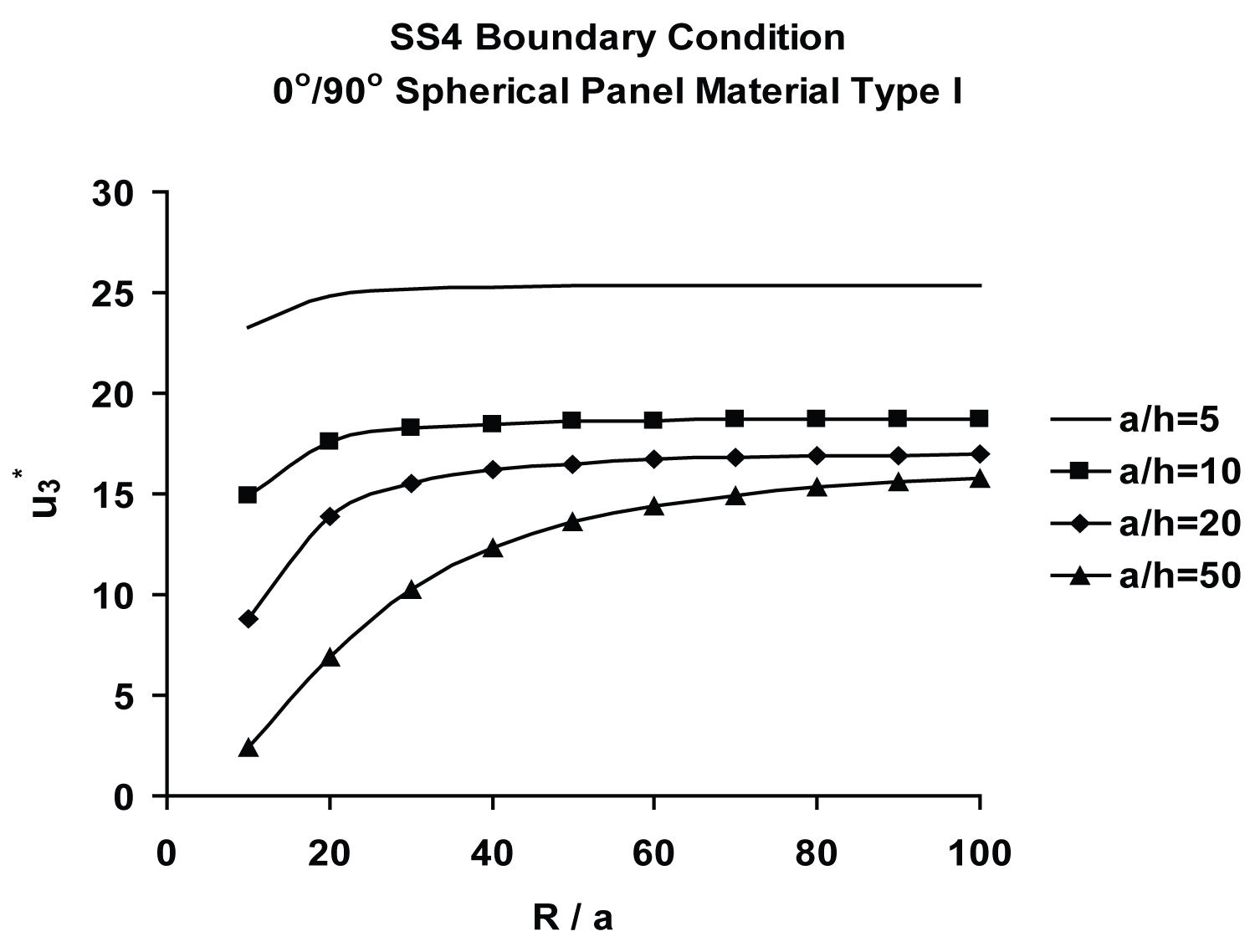
Figure 4 shows that the spherical panels exhibit progressively stiffer response with the a/h ratio in the thinner shell regime. As can be seen from these curves, the membrane action (curvature effect) is more pronounced in the deeper [0°/90°] spherical panel regime (R/a < 40). These results are also presented in Table 1, wherein variations of normalized central deflections, $u_3^{*}$, of antisymmetric [0/90] moderately deep (R/a =10) spherical panels as well as their flat plate counterparts, with a/h ratio, ranging from very thick (a/h = 5) to very thin (a/h = 100), are compared for the SS4 boundary condition. Effect of membrane action, quantified in the form of % difference between spherical and flat panels vary from some membrane action for a/h = 5 to very high membrane action for a/h = 100.

Oktem and Chaudhuri [93-94,99-100], and Chaudhuri and Seide [111] have solved boundary-value problems relating to thick to thin cross-ply plates by employing the boundary-discontinuous double Fourier series analytical technique and the finite element method, respectively, while Chaudhuri and Kabir [72] have studied their moderately thick counterparts, and Whitney and Leissa [60] have investigated thin cross-ply plates. The present computed value of 18.793 for TSDT-based central $u_3^{*}$ for the flat moderately thick (a/h = 10) SS4 panel presented in Table 1 is considerably higher than its FSDT-based SS2 counterpart, 11.55, shown in Table 4 of Chaudhuri and Kabir [72], the difference being as large as 38.54%.

Chaudhuri and Kabir [80,115], and Seide and Chaudhuri [113] have investigated moderately thick and thick cross-ply shells using the boundary-discontinuous double Fourier series analytical technique and the finite element method, respectively. The present computed value of 14.881 for central $u_3^{*}$ for a/h = 10 and R/a = 10 presented in Table 1 is also considerably higher than its FSDT counterpart, 10.11, shown in Table 2 of Chaudhuri and Kabir [115], the difference being as large as 32.06%. Furthermore, as illustrated in Table 1, the difference between spherical panel and plate normalized (central) deflections are 8.56%, 20.83%, 48.46%, 85.34% and 96.09%, for a/h = 5, 10, 20, 50 and 100, respectively. These results suggest that while the inter-laminar shear deformation or thickness-shear effect is dominant in the thick shell regime (a/h ≤ 10), the curvature effect (membrane action) dominates in its thinner counterpart.

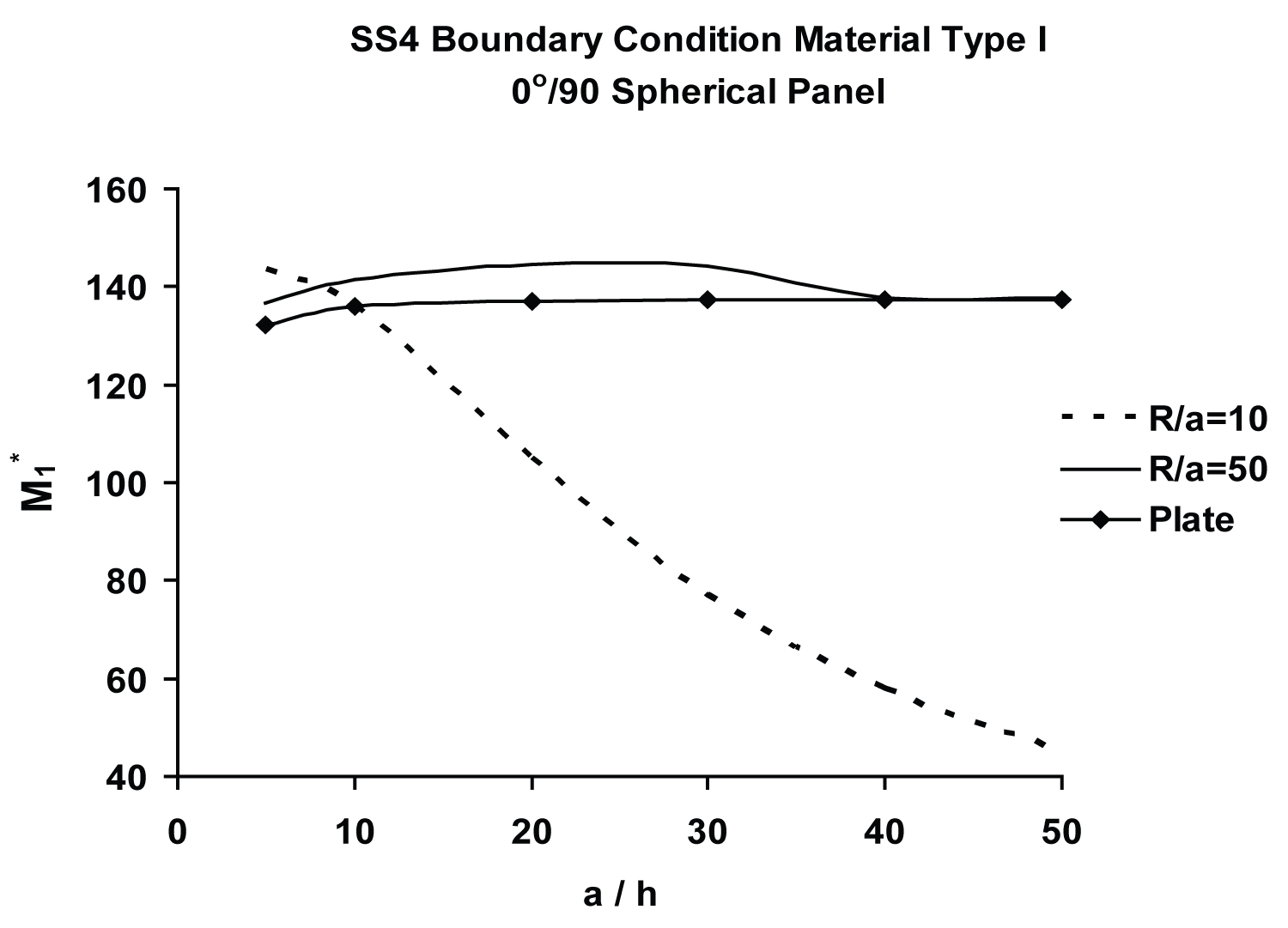
Figure 5 exhibits variation, of normalized central moment, $M_1^{*}$, of antisymmetric [0° /90°] spherical panel, with a/h, ranging from thin (a/h = 50) to very thick (a/h = 5), for moderately deep (R/a = 10) and very shallow (R/a = 50) spherical as well as flat panels. As shown in Figure 5, central moment, $M_1^{*}$, of [0°/90°] spherical panel first increases with a/h in the thick shell regime, and then drops fairly rapidly in the thinner one. The present computed value of 136.373 for central moment, $M_1^{*}$, for a/h = 10 and R/a = 10 presented in Table 2 is substantially higher than its FSDT counterpart, 77.53, shown in Table 2 of Chaudhuri and Kabir [115], the difference being a whopping 43.15%. Furthermore, as illustrated in Table 2, the difference between spherical panel and plate (central) moments for SS4 boundary condition are 8.52%, 0.17 %, 23.41%, 67.04% and 85.68% for a/h = 5, 10, 20, 50 and 100, respectively. These results suggest that while the inter-laminar shear deformation effect is dominant in the thicker shell regime (a/h ≤ 20), the curvature effect (membrane action) progressively dominates in its thinner counterpart.

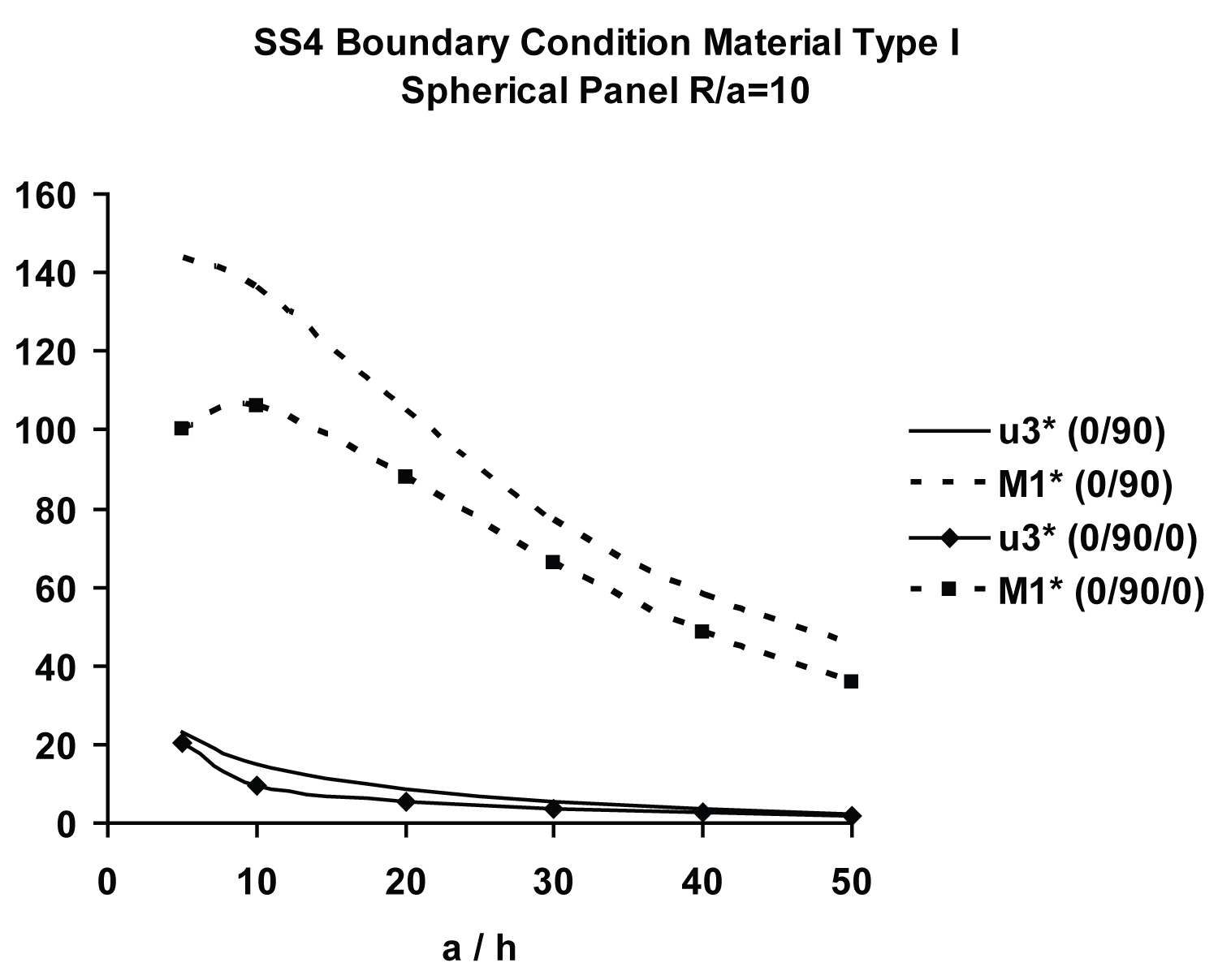
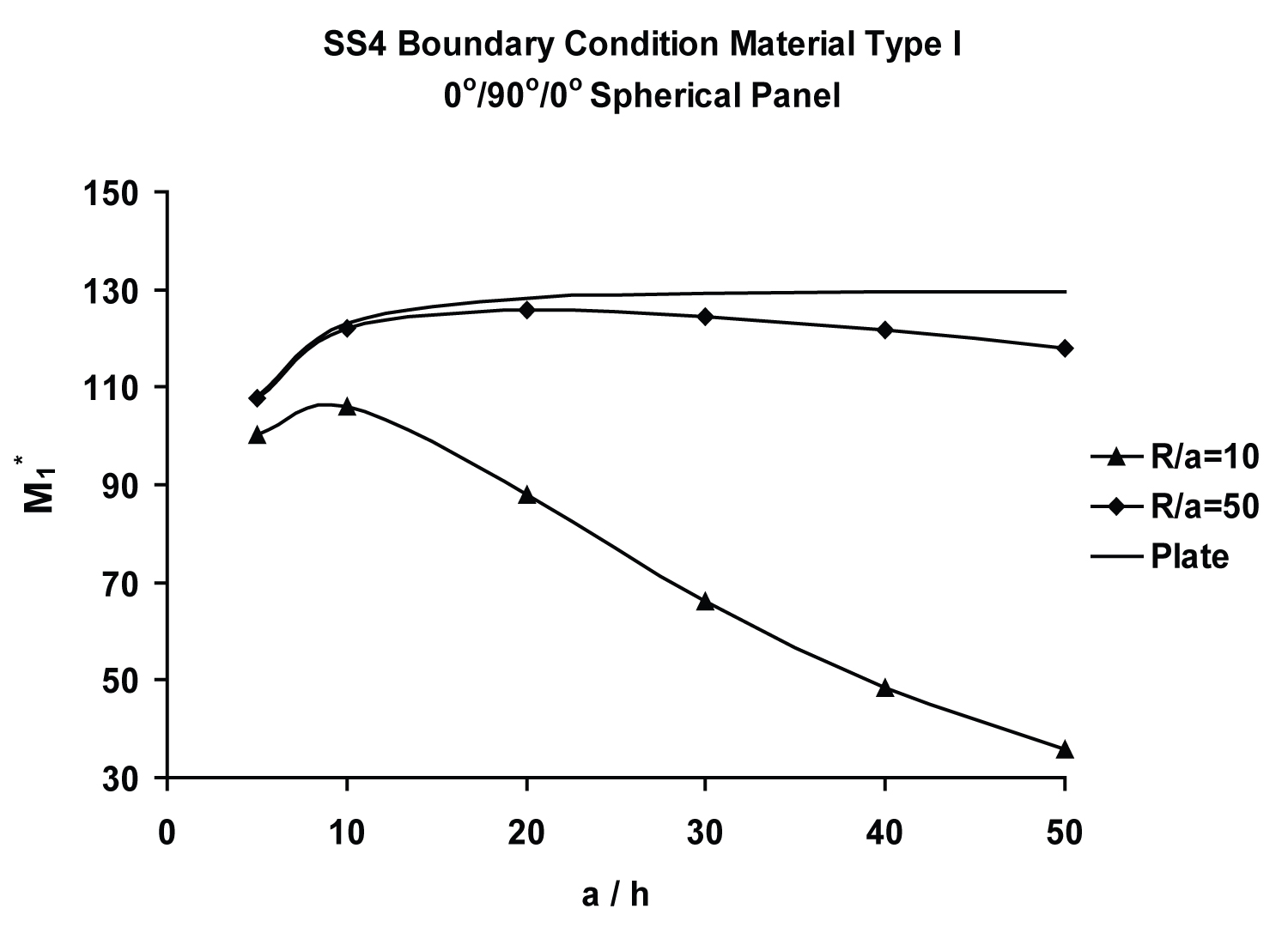
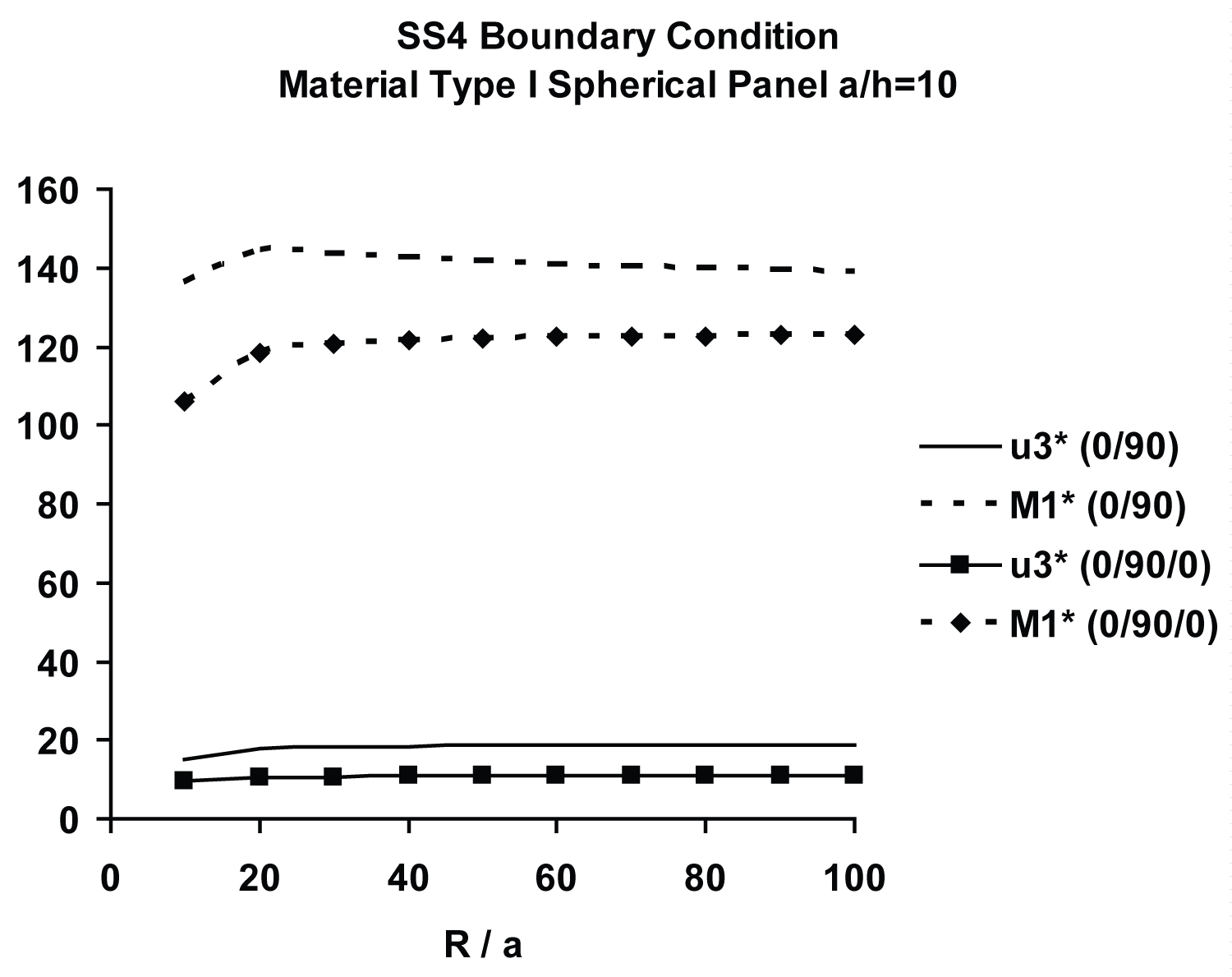
Figure 6 compares the variations of normalized central deflection, $u_3^{*}$, and central moment, $M_1^{*}$, between symmetric and antisymmetric moderately deep (R/a = 10) spherical panels, with respect to a/h ratio. It is important to note that the normalized central moment, $M_1^{*}$, is greatly influenced by the a/h ratio. Figure 7 exhibits variation of $M_1^{*}$ of the symmetric [0/90/0] spherical panel with a/h, ranging from thin (a/h = 50) to very thick (a/h = 5), for moderately deep (R/a = 10) and very shallow (R/a = 50) spherical as well as flat panels. The central $u_3^{*}$ and $M_1^{*}$ curves for the [0/90/0] spherical panel closely resemble their FSDT-based moderately thick counterparts, shown in Figure 7 of Chaudhuri and Kabir [115]. The present computed value of 9.388 (respectively, 106.108) for central $u_3^{*}$ (respectively, $M_1^{*}$) for a spherical panel (a/h = 10 and R/a = 10) with SS4 boundary constraint, presented in Table 3 (respectively, Table 4), is in reasonably close agreement with its FSDT counterpart, 9.17 (respectively, 106.79), shown in Table 3 of Chaudhuri and Kabir [115], the difference being 2.32% (resp. -0.64%). Furthermore, as illustrated in Table 3 (respectively, Table 4), the difference between spherical panel and plate (central) deflections (respectively, moments) are 7.51% (respectively, 7.42%), 13.88% (respectively, 13.73%), 31.59% (respectively, 31.25%), 73.05% (respectively, 72.27%) and 92.58% (respectively, 91.59%) for a/h = 5, 10, 20, 50 and 100, respectively.

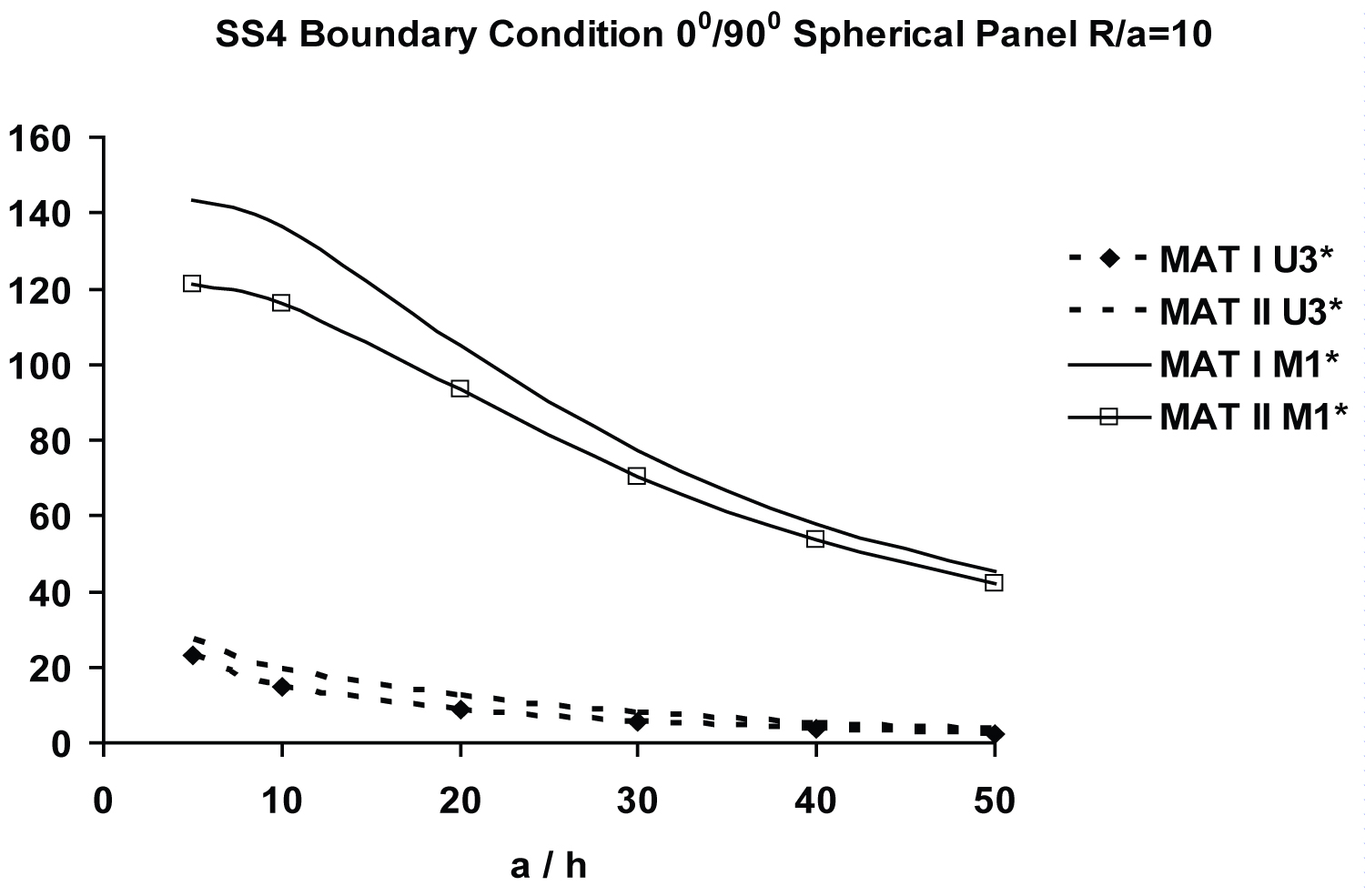
Figure 8 compares the normalized central deflections, $u_3^{*}$, and central moments, $M_1^{*}$, of antisymmetric [0/90] moderately deep (R/a = 10) spherical panels with SS4 boundary condition possessing two different material properties. As expected, stiffer material (M1) decreases the normalized central deflection and increases the normalized central moment.

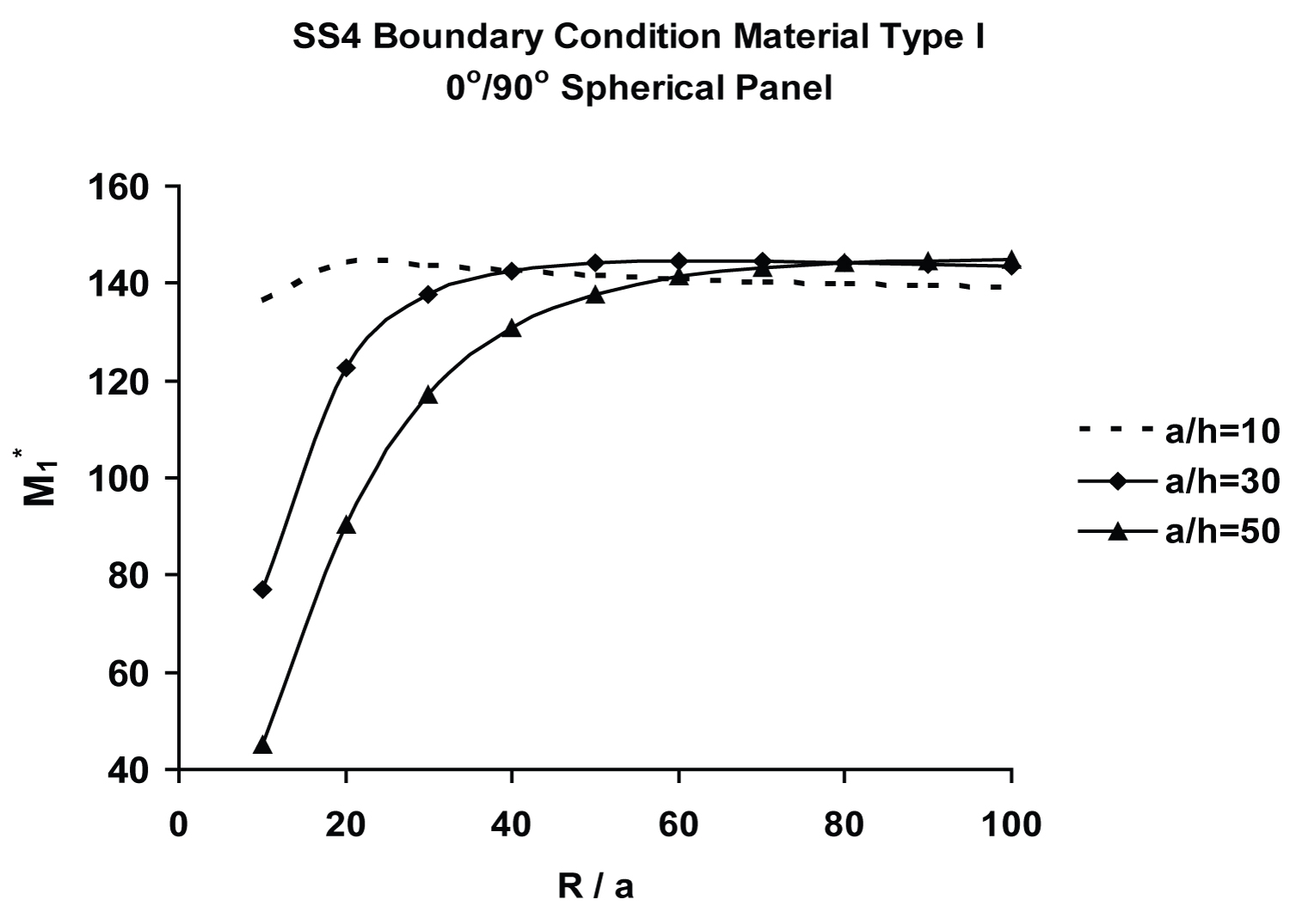
Figure 9 exhibits variation of $u_3^{*}$ of [0/90] spherical panel, with R/a ratio. As can be seen from these graphs, the membrane action (curvature effect) is more pronounced in the deeper [0/90] spherical panel regime (R/a < 40), also progressively increasing with the a/h ratio. Figure 10 shows the variations of central deflection, $u_3^{*}$, and moment, $M_1^{*}$, of both symmetric and antisymmetric relatively thick (a/h =10) spherical panels with respect to R/a ratio. These plots show that the characteristic of the deflection pattern of an anti-symmetric [0/90] curved panel is different from its symmetric [0/90/0] counterpart. Curvature effect (membrane action) is also responsible for the decreased normalized response in both symmetric and antisymmetric type spherical panels for R/a ≤ 20. This notwithstanding, these results provide a clear indication of the tie-bar effects, arising out of bending-stretching coupling, which has a complex interaction with the membrane action, caused by the curvature effect, in the presence of surface-parallel edge restraint (SS4 boundary condition). It is interesting to point out here that there are two types of bending-stretching coupling in the TSDT: (i) Third-order bending-stretching, which arises out of non-vanishing Eij's, that can only be captured by the TSDT, and (ii) First-order bending-stretching coupling, caused by non-vanishing Bij's, which is generally covered by all laminated shell theories. The latter type has been investigated in-depth in the context of axi-symmetric deformation of thin [119-123] as well as moderately thick [124-126] variously laminated cylindrical shells, in addition to static and dynamic tests on flat laminates [62,106,127]. It is further noteworthy in this context that the bending-stretching coupling may either cause surface-parallel compression ("beam-column" effect) or surface-parallel stretching (called "tie-bar" effect) in a panel subjected to bending. The former has a softening effect while the latter has a stiffening or hardening effect on the laminated panel response [123]. It also is important to note that for the normalized central moment, $M_1^{*}$, the influence of curvature becomes progressively less dominant for R/a > 20. Figure 11 depicts the variation of $M_1^{*}$ of [0°/90°] spherical panel, with R/a ratio, for three different a/h ratios. For the two thinner panels, this threshold shifts upward, i.e., R/a ≥ 38 and 60 for a/h = 30 and 50, respectively.

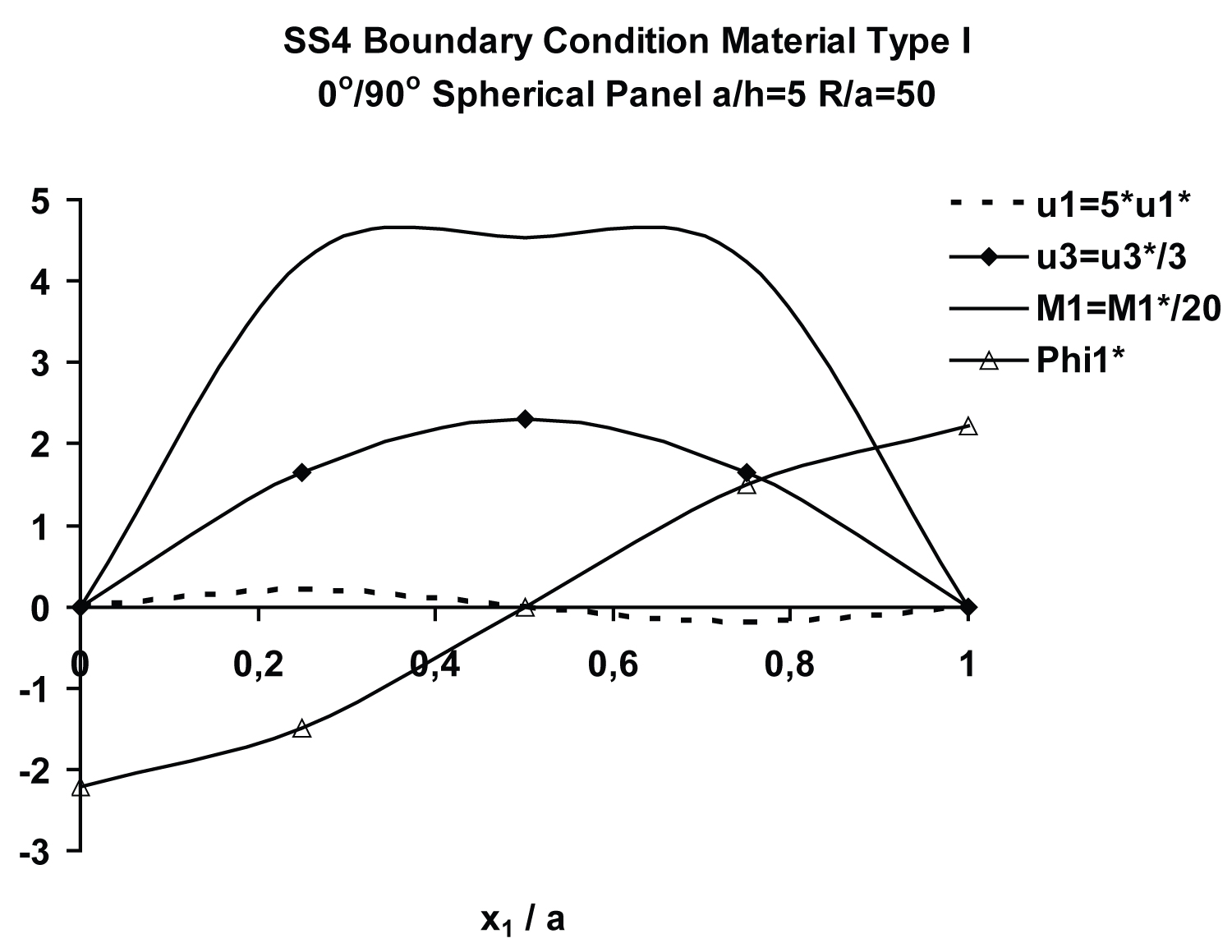
Variations of $u_1^{*},u_3^{*},{\phi }_1^{*}$ and $M_1^{*}$ computed at $x_2=b/2$ and along $x_1=0$ to a, are shown in Figure 12. Transverse displacement, $u_3^{*}$, and central moment, $M_1^{*}$, reach their maximum magnitudes at the center of the panel, where surface-parallel displacement, $u_1^{*}$, and rotation, ${\phi }_1^{*}$, vanish. $u_1^{*}$ reaches its maximum magnitude at $x_1=L/4$ and x₁ = 3L/4, while the rotation, ${\phi }_1^{*}$, reaches its maximum value at $x_1=0$ and $x_1=L$. As dictated by the boundary conditions, surface-parallel displacement, $u_1^{*}$, vanishes at the boundaries.

Comparison between SS1 and SS4 Boundary Conditions

Figure 13 and Figure 14 present variations of the relative difference, in central deflections, , with a/h ratio for symmetric ([0/90/0] and [0/90]s) and antisymmetric [0°/90°] and for two different material properties, between SS1 and SS4 boundary conditions. For the calculation of relative difference (% difference) between the two boundary conditions, the following formula is used:

$$\%Difference=\left|\frac{SS4-SS1}{SS1}\right|100$$

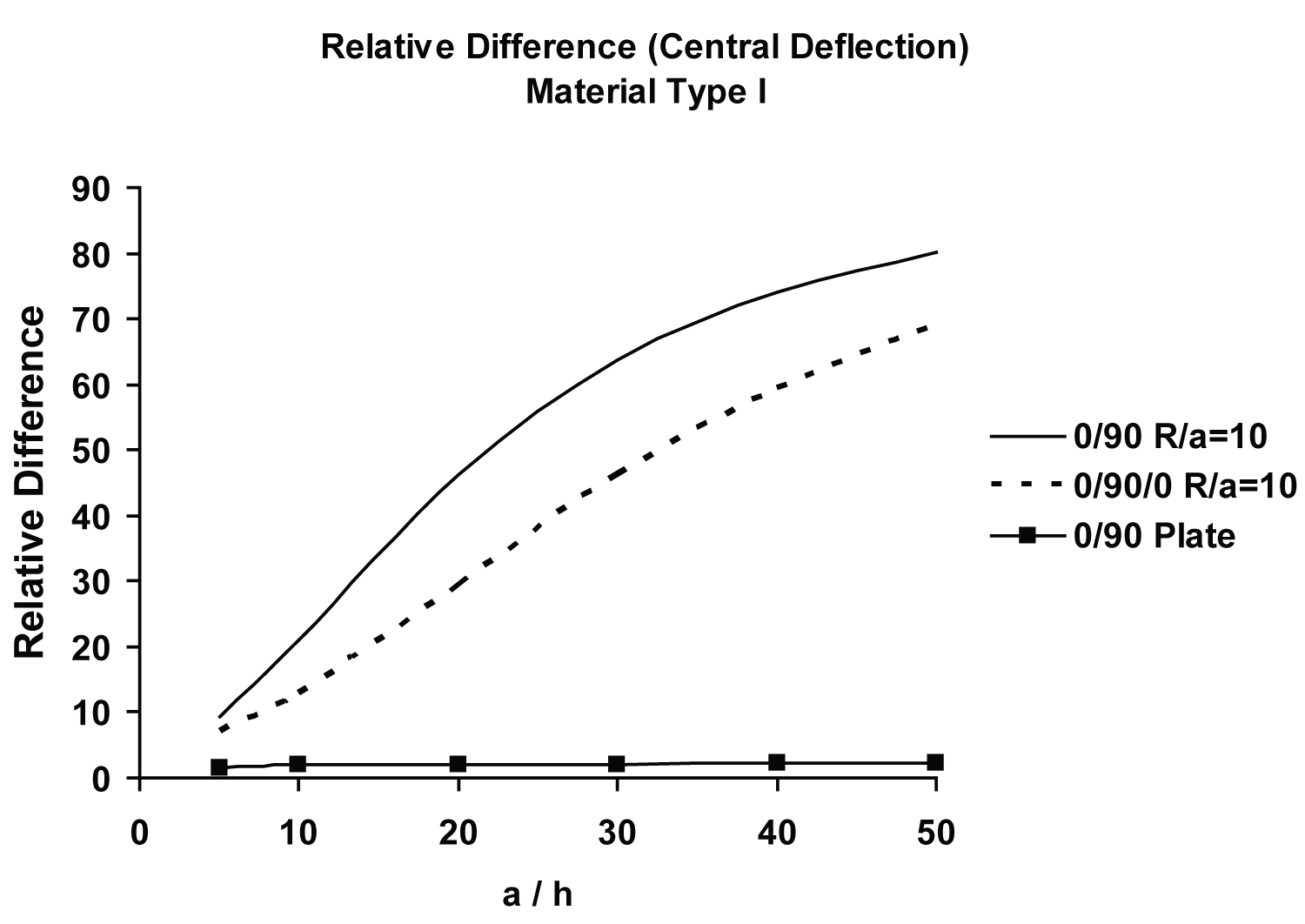
The relative difference in central deflections, $u_3^{*}$, between the two boundary conditions tends to increase with the increasing values of a/h (thinner structures). This difference is, however, somewhat less pronounced in case of symmetric laminations than their asymmetric counterpart.

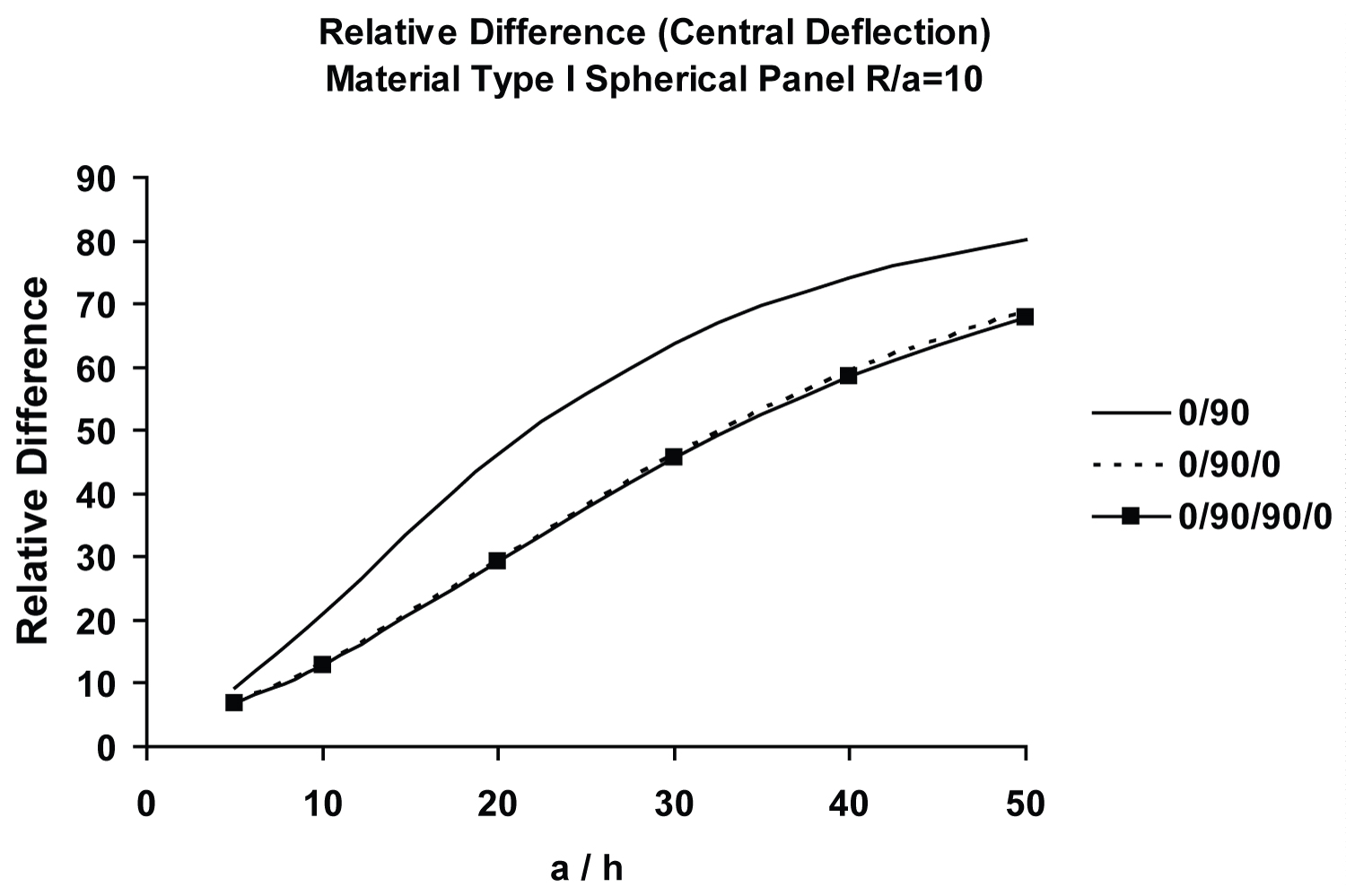
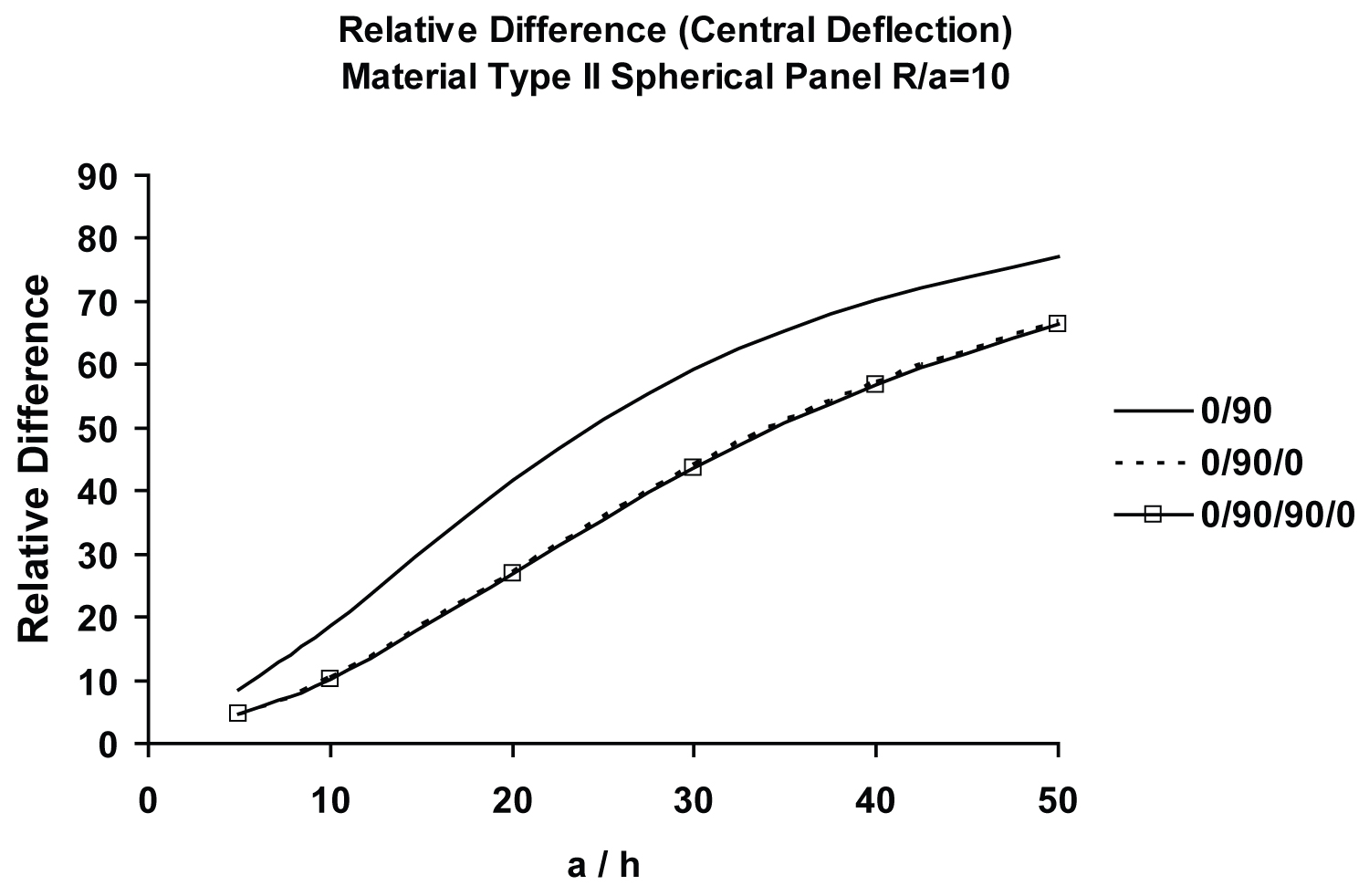
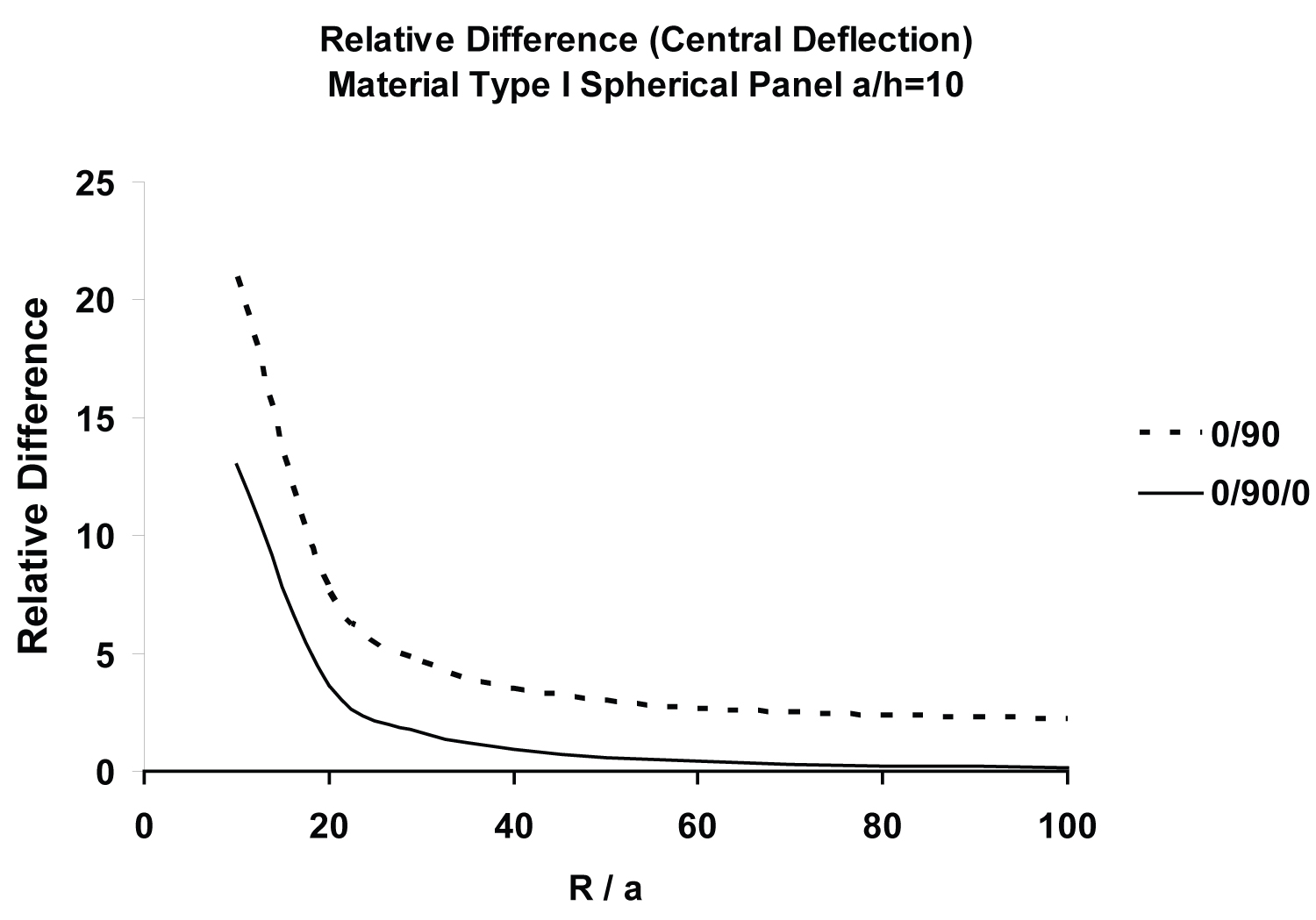
Variations of the relative difference in central deflections, $u_3^{*}$, with a/h and R/a ratios, respectively, for symmetric ([0/90/0]) and antisymmetric [0/90] spherical panel are shown in Figure 15 and Figure 16. For comparison, antisymmetric [0/90] plate results have also been regenerated [100]. As shown in both the plots, membrane (curvature) action exerts an important effect on the surface-parallel boundary constraints particularly for R/a < 20. This effect diminishes with the increase of R/a, as shown in Figure 16 (flat panel case). These results are also presented in Table 5, wherein variations of normalized central deflections, $u_3^{*}$, of antisymmetric [0/90] moderately deep (R/a = 10) spherical panels as well as their flat plate counterparts, with a/h ratio, ranging from very thick (a/h = 5) to very thin (a/h = 100), are compared for three different surface-parallel edge constraints: SS1, SS3 and SS4. Effect of membrane action, quantified in the form of % difference between spherical and flat panels vary from some membrane action for a/h = 5 to very high membrane action for a/h = 100. Effect of surface-parallel edge restraint is seen to be insignificant in the entire range of a/h ratios. It may be pointed out in this context, that "FSDT-based convergence plots of an antisymmetric cross-ply spherical panel, with the SS2 boundary condition…, are numerically too close to their SS4 counterparts…. This is because both the conditions prescribe un = 0 (instead of Nn = 0) at a boundary - a choice that appears to have a major influence on the response of antisymmetric cross-ply panels under uniform loads. Likewise, the convergence characteristics of the response quantities for antisymmetric cross-ply panels, with SS1 and SS3 boundary conditions…, where Nn = 0, instead of un = 0, is prescribed at a boundary, are numerically very close" [80,115].

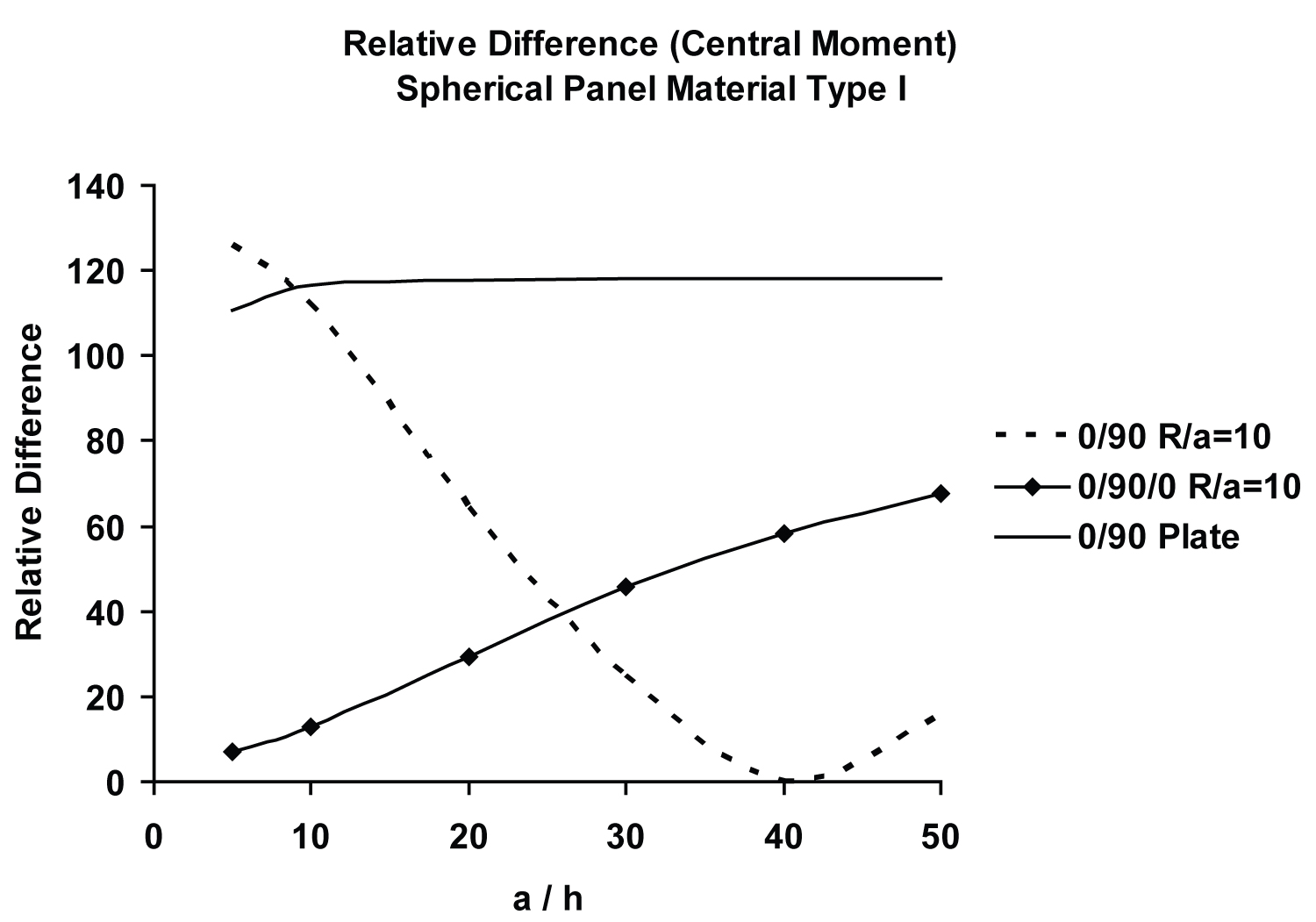
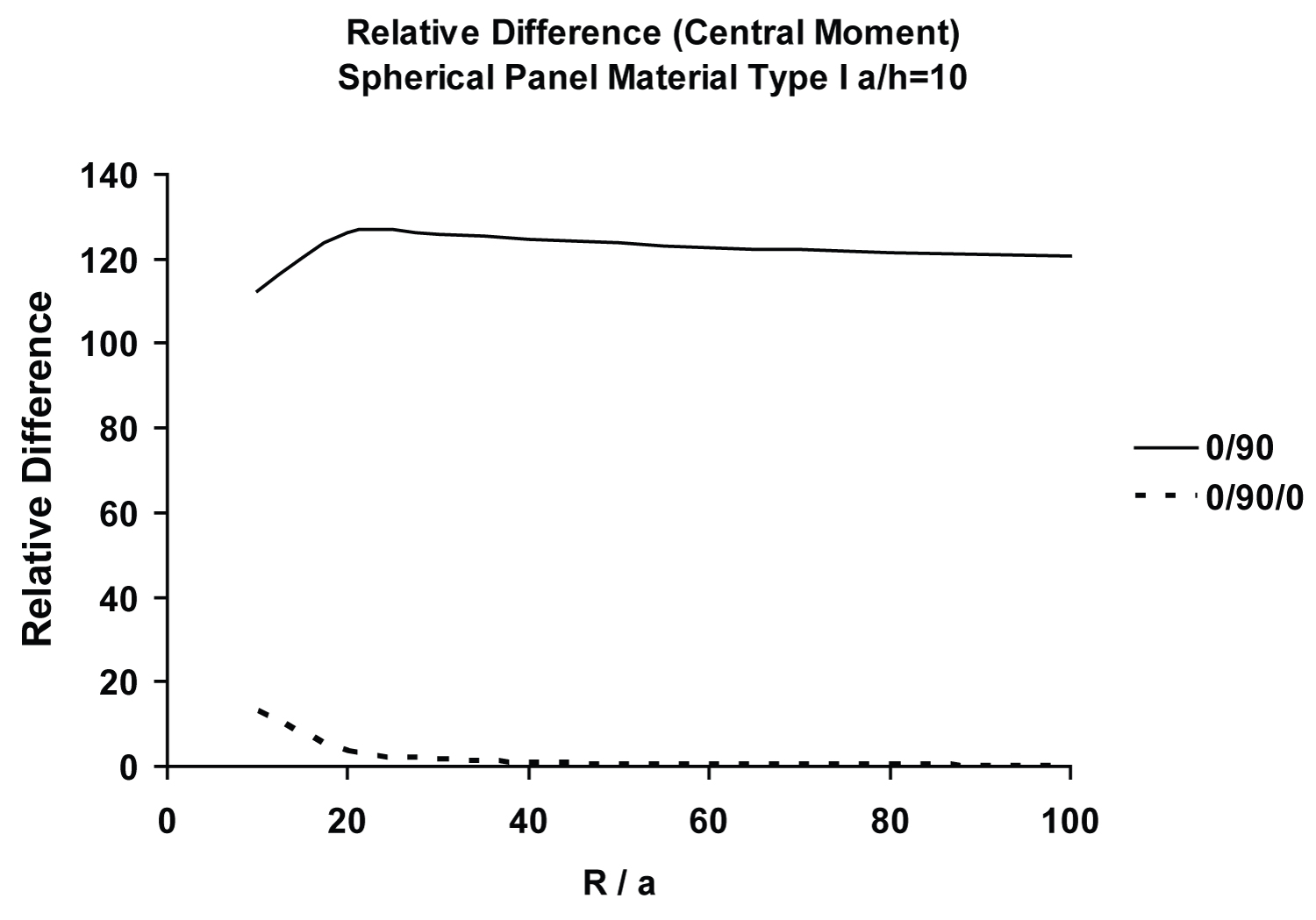
Figure 17 and Figure 18 show the relative difference in central moment, $M_1^{*}$, of both symmetric and antisymmetric moderately deep (R/a = 10) spherical panels with respect to a/h and R/a ratios, respectively. The aforementioned curvature effect is also clearly visible in Figure 18. It is noteworthy that the membrane action due to the effect of curvature has a complex interaction with the bending-stretching type coupling effect, caused by the asymmetry of lamination. This interaction is stronger in the case of surface-parallel displacement boundary constraint, i.e., $u_n=0$ prescribed at an edge $x_n$ = constant (e.g., SS4) as compared to its absence, i.e., $N_n=0$ (e.g., SS1), which is an illustration of the beam-column effect. For example, the bending-stretching type coupling has a highly pronounced interaction with the type of surface-parallel boundary constraint, imposed by e.g., SS4 as compared to SS1 type simply supported boundary conditions, prescribed at all four edges.

Comparisons of results, computed using three leading shear deformation theories, and the classical lamination theory

Table 5 and Table 6 depict comparisons of normalized central deflections, $u_3^{*}$, and moments, $M_1^{*}$, respectively, of symmetric [0/90/0] plates under uniform load for different a/h ratios, computed using three leading shear deformation theories, namely the LCST or Zig-zag theory, TSDT, and FSDT, and the classical lamination theory. Degree of shear flexibility is defined as follows:

$\%DegreeofShearFlexibility=\frac{SDTx-CLT}{CLT}100,x=Zig-ZagorHSDT$

Table 5 shows that the LCST or zig-zag theory yields much greater shear-flexibility than the TSDT in terms of the computed normalized central deflection, $u_3^{*}$ (344.295% vs. 231.514%) for a very thick [0/90/0] plate (a/h = 4). The difference in the degree of shear flexibility decreases with the increase of a/h ratio. Table 6 shows that the LCST or zig-zag theory yields somewhat greater shear-flexibility than the TSDT in terms of the computed normalized central moment, $M_1^{*}$ (-22.119% vs. -16.32%). Again, the difference in the degree of shear flexibility diminishes with the increase of a/h ratio. Computed zig-zag theory and TSDT (0.149% vs. -0.839%) results are very close for a/h = 20.

Table 7 and Table 8 depict comparisons of normalized central deflections, $u_3^{*}$, and moments, $M_1^{*}$, respectively, of symmetric [0°/90°/0°] deep cylindrical panels (R/a = 3) under uniform load for different a/h ratios, computed using three leading shear deformation theories (SDT). Since very thin shells are, unlike their plate counterparts, predominantly deformed by the membrane action due to the curvature effect, which has a hardening or stiffening effect, the CLT is not very useful in serving as a baseline for comparison of shear deformation theories. Relative degree of shear flexibility is, therefore, defined as follows:

$$\%\mathrm{Re}lativeDegreeofShearFlexibility=\frac{SDTx-FSDT}{FSDT}100,\begin{array}{cc}x=Zig-ZagorHSDT& \end{array}$$

Table 7 shows that the LCST or zig-zag theory yields much greater shear-flexibility than the TSDT in terms of the computed normalized central deflection, $u_3^{*}$ (46.079% vs. 9.767%) for a very thick [0°/90°/0°] cylindrical panel (a/h = 4). The difference in the relative degree of shear flexibility progressively diminishes with the increase of a/h ratio. Table 8 shows that the LCST or zig-zag theory yields somewhat greater shear-flexibility than the TSDT in terms of the computed normalized central moment, $M_1^{*}$ (-8.494% vs. -1.169%). Again, the difference in the relative degree of shear flexibility progressively diminishes with the increase of a/h ratio.

Table 9 and Table 10 portray comparisons of normalized central deflections, $u_3^{*}$, and moments, $M_1^{*}$, respectively, of symmetric [0°/90°/0°] deep spherical panels (R/a = 3) under uniform load for different a/h ratios, computed using three leading shear deformation theories. Relative degree of shear flexibility is defined as follows:

$$\%\mathrm{Re}lativeDegreeofShearFlexibility=\frac{SDTx-FSDT}{FSDT}100,\begin{array}{cc}x=Zig-ZagorHSDT& \end{array}$$

Table 9 shows that the LCST or zig-zag theory yields much greater shear-flexibility than the TSDT in terms of the computed normalized central deflection, $u_3^{*}$ (51.523% vs. 9.412%) for a very thick [0/90/0] spherical panel (a/h = 4). The difference in the relative degree of shear flexibility progressively diminishes with the increase of a/h ratio. Table 10 shows that the LCST or zig-zag theory yields somewhat greater shear-flexibility than the TSDT in terms of the computed normalized central moment, $M_1^{*}$ (-8.451% vs. -1.497%). Again, the difference in the relative degree of shear flexibility progressively diminishes with the increase of a/h ratio.

Comments on the reliability of the finite element methods (FEM)

Finally, reliability of the finite element method, based on the assumed displacement potential energy approach, in the neighborhood of stress discontinuities and stress singularities has been discussed by Whitcomb, et al. [128] (at the free edge in a laminated composite), and Chaudhuri and co-workers [129-137] (at the circumferential corner line of an internal circular cylindrical hole). Whitcomb, et al. [128] have concluded that "the finite element method yielded accurate solutions everywhere except in a region involving the elements closest to the stress discontinuity or singularity and that this region can be made arbitrarily small by refining the finite element model". Chaudhuri [129-133] has probed into the issue much deeper. His conclusion re-affirms, to a rather milder degree, the conclusion reached in the case of its laminate counterpart [133-137] in regards to the accuracy (or lack thereof) of the stresses (more accurately, the stress gradients) computed using the conventional (assumed displacement potential energy based) finite element analysis and computed FEM-based post-processing analysis results for transverse shear stresses in the vicinity of a stress singularity, such as the circumferential corner line of an internal circular/elliptical cylindrical hole.

In conclusion, numerical solutions, based on finite elements methods (FEM), finite difference, boundary elements methods (BEM) and so on, have been presented by numerous authors. However, their resolution is not fine enough to yield definitive results at a line of discontinuity. Only the boundary-discontinuous Fourier analysis of the present type can reproduce precisely the discontinuities in displacement functions and/or their partial derivatives at the edges.

Conclusions

The key conclusions that emerge from the present numerical results can be summarized as follows:

i. The central deflection shows a rapid and monotonic convergence, while the central moment shows an initially oscillatory convergence. The latter is possibly due to the presence of a discontinuity (complementary boundary constraint) in the derivative of the displacement in expression of the moment. In addition, because of the same reason, the computed solutions for SS4 boundary conditions converge less rapidly than their SS1 counterpart.

ii. The length-to-thickness ratio, $a/h$, has a significant effect on the computed results in the moderately thick to thick panel regime (a/h < 20). This is due to the effect of transverse (interlaminar) shear deformation.

iii. The radius-to-length ratio $R/a$ has a pronounced effect on the response of curved cross-ply panels. This effect is progressively more pronounced in the deeper shell regime $(R/a<40)$ for a given a/h.

iv. The effect of the transverse shear deformation is compensated to a certain extent by the bending-stretching coupling effect - a characteristic of antisymmetric laminates.

v. The difference (normalized) in central deflection between the SS1 and SS4 boundary conditions increases with the increasing values of a/h (thinner structures). This difference is, however, somewhat less pronounced in case of symmetric laminates than their asymmetric counterpart.

vi. The membrane action due to the effect of curvature has a complex interaction with the bending-stretching type coupling effect, caused by the asymmetry of lamination. This interaction is stronger in the case of surface-parallel displacement boundary constraint, i.e., $u_n=0$ prescribed at an edge $x_n$ = constant (e.g., SS4) as compared to its absence, i.e., $N_n=0$ (e.g., SS1). This is an illustration of the beam-column/tie-bar effect. For example, the bending-stretching type coupling has a highly pronounced interaction with the type of surface-parallel boundary constraint, imposed by e.g., SS4 as compared to SS1 type simply supported boundary conditions, prescribed at all four edges.

vii. The layer-wise constant shear-angle theory or zig-zag theory yields much greater shear-flexibility than the TSDT in terms of the computed normalized central deflection, $u_3^{*}$ (51.523% vs. 9.412%) for a very thick [0/90/0] spherical panel (a/h = 4). The difference in the relative degree of shear flexibility progressively diminishes with the increase of a/h ratio. Responses of cylindrical panels are similar.

viii. The layer-wise constant shear-angle theory or zig-zag theory yields somewhat greater shear-flexibility than the third order shear deformation theory in terms of the computed normalized central moment, $M_1^{*}$ (-8.451% vs. -1.497%) for a very thick [0/90/0] spherical panel (a/h = 4). Again, the difference in the relative degree of shear flexibility progressively diminishes with the increase of a/h ratio. Cylindrical panels behave in similar manners.

Suggestion for Future Research

First, although the present double Fourier series solutions are confined to general cross-ply thick hyperbolic-paraboloidal panels subjected to SS4 type simply supported boundary condition, the present methodology is general enough to be able to solve arbitrarily laminated doubly curved panels subjected to any combination of admissible boundary conditions. These problems need to be solved in the near future to provide bench-mark analytical solutions for a variety of numerical solutions including those computing using the FEM.

Second, a boundary-value formulation based on trigonometric shear deformation theory [90] for laminated anisotropic doubly curved panels of various ply-orientations, subjected to arbitrary boundary constraints, can also solved using the present approach. Third and more important, the present and future TSDT-based results for laminated anisotropic doubly curved panels can be compared with their counterparts computed using the zig-zag theory (or layer-wise constant shear angle theory (LCST))-based FEM [30,110-114,129-137].

Fourth, computation of the normalized central deflections by employing both commercial FEA codes (e.g., ABAQUS and ANSYS) and the current MATLAB code based on the boundary continuous double Fourier series, for all parameters, and demonstrating the main differences thus obtained, is an important topic for further research.

Fifth, experimental results are needed to validate the present as well as other higher order shear deformation theory based models for laminated anisotropic panels of negative Gaussian curvature, in a manner that can be considered as extensions of Refs. [62,106-108,127].

Sixth, isotropic and laminated anisotropic doubly curved panels, weakened by through [8,114] and part-through holes, both internal [114,129-131,133-136] and external [132,137], have not been investigated like their flat and cylindrical panel counterparts. This is an extremely important area for further research.

Seventh, significant progress has been reported by Kim and Chaudhuri [10,14,20,26-28,32], Hsia and Chaudhuri [11], Chaudhuri and Hsia [12,13], Chaudhuri and Kim [4,24,25,33,34], Tvergaard and Needleman [31], Chaudhuri [29-30,35-38,44,116], Chaudhuri, et al. [45,46], and Chaudhuri and Abu-Arja [118], on large deflection, material nonlinearity, nonlinear resonance (eigenvalue), post-buckling, localization/delocalization, shear crippling type propagating instability, and compression fracture of composite shells/panels of cylindrical geometry. In future, we intend to extend such studies to laminated anisotropic doubly curved panels.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Conflicts of Interest/Competing Interests

The authors have no conflicts of interest to declare that are relevant to the content of this article.

Availability of Data and Material

Not applicable.

Code Availability

The code is proprietary; will not be made available at this time.

References

1. Laetsch ND (1993) Composite hull increases submarine's range of action. Composites 24: 314.
2. Garala HJ (1989) Structural evaluation of 8-inch diameter graphite-epoxy composite cylinders subjected to external hydrostatic compressive loading. DTRC (NSWC) Report 89/016.
3. Garala HJ, Chaudhuri RA (1993) Structural evaluation of advanced composite thick-section cylinders under biaxial compression. Mechanics of Thick Composites, ASME (edited by Y. Rajapakse) 162: 227-236.
4. Chaudhuri RA, Kim D (2009) Effects of thickness and transverse shear modulus nonlinearity on the post-localization response of an imperfect cross-ply ring. Composite Structures 88: 83-96.
5. Kim D, Chaudhuri RA (2007) Effect of thickness on buckling of perfect cross-ply rings under external pressure. Composite Structures 81: 525-532.
6. Noor AK, Hartley SJ (1977) Nonlinear shell analysis via mixed isoparametric elements. Computers & Structures 7: 615-626.
7. Chaudhuri RA (1987) A simple and efficient shear-flexible plate bending element. Computers & Structures 25: 817-824.
8. Chaudhuri RA, Seide P (1986) Triangular element for analysis of perforated plates under in plane and transverse loads. Computers & Structures 24: 87-95.
9. Chaudhuri RA (1988) A degenerate triangular shell element with constant cross-sectional warping. Computers & Structures 28: 315-325.
10. Kim D, Chaudhuri RA (1995) Full and von Karman geometrically nonlinear analyses of laminated cylindrical panels. AIAA Journal 33: 2173-2181.
11. Hsia RL, Chaudhuri RA (1996) Geometrically nonlinear analysis of a cylindrical shell using surface-parallel quadratic elements. Computers & Structures 61: 1143-1154.
12. Chaudhuri RA, Hsia RL (1999) Effect of thickness on the large deflection behavior of shells. AIAA Journal 37: 403-405.
13. Chaudhuri RA, Hsia RL (1999) Effect of thickness on the large elastic deformation behavior of laminated shells. Composite Structures 44: 117-128.
14. Kim D, Chaudhuri RA (2006) Post buckling of moderately thick imperfect rings under external pressure. ASCE J Eng Mech 132: 1273-1276.
15. To CWS, Liu ML (2001) Geometrically nonlinear analysis of layer wise anisotropic shell structures by hybrid strain based lower order elements. Finite Elements in Anal Des 37: 1-34.
16. Yang HTY, Saigal S, Masud A, et al. (2000) A survey of recent shell finite elements. Int J Numer Methods Eng 47: 101-127.
17. Kabir HRH, Askar H, Chaudhuri RA (2003) Thermal buckling response of shear-flexible laminated anisotropic plates using a three-node isoparametric element. Composite Structures 59: 173-187.
18. Sheng HY, Ye JQ (2003) A three-dimensional state space finite element solution for laminated composite cylindrical shells. Comput Methods in Appl Mech Eng 192: 2441-2459.
19. Reddy JN (2004) Mechanics of laminated composite plates and shells, theory and Practice. 2nd edition, CRC Press Boca Raton Florida.
20. Kim D, Chaudhuri RA (2009) Post buckling behavior of symmetrically laminated thin shallow circular arches. Composite Structures 87: 101-108.
21. Sabik A, Kreja I (2015) Thermo-elastic non-linear analysis of multilayered plates and shells. Composite Structures 130: 37-43.
22. Kulikov GM, Mamontov AA, Plotnikova SV, et al. (2016) Exact geometry solid-shell element based on a sampling surfaces technique for 3D stress analysis of doubly-curved composite shells. Curved and Layered Structures 3: 1-16.
23. Levyakov SV, Kuznetsov VV (2017) Invariant-based formulation of a triangular finite element for geometrically nonlinear thermal analysis of composite shells. Composite Structures 177: 38-53.
24. Chaudhuri RA, Kim D (1997) On propagation of shear crippling (kink band) instability in a long imperfect laminated composite cylindrical shell under external pressure. Int J Solids and Struct 34: 3455-3486.
25. Chaudhuri RA, Kim D (2003) Localization and shear-crippling instability in a thick imperfect laminated composite ring under hydrostatic pressure. Int J Solids Struct 40: 7063-7092.
26. Kim D, Chaudhuri RA (2005) Influence of localized imperfection on the instability of isotropic/cross-ply cylindrical shells/rings under external pressure. Composite Structures 67: 57-70.
27. Kim D, Chaudhuri RA (2005) Influence of localized imperfection on the instability of isotropic/cross-ply cylindrical shells/rings under external pressure. Composite Structures 67: 57-70.
28. Kim D, Chaudhuri RA (2007) Effect of lamination sequence on the localization and shear crippling instability in thick imperfect cross-ply rings under external pressure. Composite Structures 80: 504-513.
29. Chaudhuri RA (2008) Effects of fiber misalignment and transverse shear modulus on localization and shear crippling instability in thick imperfect cross-ply rings under external pressure. Composite Structures 82: 587-599.
30. Chaudhuri RA (2008) A nonlinear zigzag theory for finite element analysis of highly shear-deformable laminated anisotropic shells. Composite Structures 85: 350-359.
31. Tvergaard V, Needleman A (2000) Buckling localization in a cylindrical panel under axial compression. W T Koiter Commemorative Issue, Int J of Solids & Struct 37: 6825-6842.
32. Kim D, Chaudhuri RA (2005) Localized buckling of a bilinear elastic ring under external pressure. ASCE J Eng Mech 131: 221-224.
33. Chaudhuri RA, Kim D (2008) Influence of localized imperfection and surface-parallel shear modulus nonlinearity on the instability of a thin cross-ply cylindrical shell under external pressure. Composite Structures 82: 235-244.
34. Chaudhuri RA, Kim D (2008) Sensitivity of the post-localization response of a thick cross-ply imperfect ring to transverse Young's modulus nonlinearity. Composite Structures 84: 44-55.
35. Chaudhuri RA (2006) Localization, delocalization and compression fracture in moderately thick transversely isotropic rings under external pressure. ASME J Eng Mater and Tech 128: 603-610.
36. Chaudhuri RA (2015) Effects of thickness and fibre misalignment on compression fracture in cross-ply (very) long cylindrical shells under external pressure. Proceedings of the Royal Society A London, 20150147.
37. Chaudhuri RA (2016) Stress intensity factor and energy release rate of externally pressurized thick cross-ply (very) long cylindrical shells with low-hardening transverse shear modulus nonlinearity. Eng Fract Mech 151: 138-160.
38. Chaudhuri RA (2016) Localization, delocalization and compression fracture in externally pressurized thick cross-ply (very) long cylindrical shells with material non-linearity: A multi-scale and multi-physics analysis. Inter J Non-Linear Mech 84: 68-81.
39. Raju IS, Chen T (2003) A computationally efficient meshless local Petrov-Galerkin method for axisymmetric problems. AIAA-2003-1673.
40. Edalati H, Soltani B (2018) Elastic analysis of arbitrary shape plates using Meshless local Petrov-Galerkin method. Wind & Structures 27: 235-245.
41. Tornabene F, Fantuzzi N, Viola E, et al. (2014) Static analysis of doubly-curved anisotropic shells and panels using cuf approach, differential geometry and differential quadrature method. Composite Structures 107: 675-697.
42. Tornabene F, Fantuzzi N, Viola E, et al. (2013) Radial basis function method applied to doubly-curved laminated composite shells and panels with a general higher-order equivalent single layer formulation. Composites Part B: Engineering 55: 642-659.
43. Stenger F, Chaudhuri RA, Chiu J (2000) Sinc solution of boundary integral form for two-dimensional bi-material elasticity problems. Composites science and technology 60: 2197-2211.
44. Chaudhuri RA (2018) A nonlinear resonance (eigenvalue) approach for computation of elastic collapse pressure of a harmonically imperfect moderately thin ring. Thin-Walled Structures 127: 344-353.
45. Chaudhuri RA, Kim D, Pavliga JR (2008) A nonlinear resonance (eigenvalue) approach for computing elastic collapse pressure of a moderately thick cross-ply imperfect ring. Composite structures 82: 117-126.
46. Chaudhuri RA, Pavliga JR, Kim D (2008) Effects of thickness and modal imperfection amplitude on elastic collapse pressure of a cross-ply imperfect ring. Composite Structures 86: 370-384.
47. Chaudhuri RA (1986) An equilibrium method for prediction of transverse shear stresses in a thick laminated plate. Computers & Structures 23: 139-146.
48. Chaudhuri RA, Seide P (1987) An approximate method for prediction of transverse shear stresses in a laminated shell. Int J Solids and Struct 23: 1145-1161.
49. Rohwer K, Rolfes R (1998) Calculating 3D stresses in layered composite plates and shells. Mechanics of composite materials 34: 355-362.
50. Chaudhuri RA, Seide P (1987) An approximate semi-analytical method for prediction of interlaminar shear stresses in an arbitrarily laminated anisotropic plate. Computers & Structures 25: 627-636.
51. Chaudhuri RA (1990) On the prediction of interlaminar shear stresses in a thick laminated general shell. Inter J Solids and Struc 26: 499-510.
52. Li D (2021) Layer wise theories of laminated composite structures and their applications: A Review. Arch Comput 28: 577-600.
53. Winslow AM (1951) Differentiation of Fourier series in stress solutions for rectangular plates. Q J of Mech and Appl Math 4: 449-460.
54. Chaudhuri RA (1989) On boundary-discontinuous double Fourier series solution to a system of completely coupled P.D.E.'s. Int J Eng Sci 27: 1005-1022.
55. Chaudhuri RA (2002) On the roles of complementary and admissible boundary constraints in Fourier solutions to boundary-value problems of completely coupled rth order PDES. J Sound and Vib 251: 261-313.
56. Green AE (1944) Double Fourier series and boundary value problems. Proceedings of the Cambridge Philosophical Society 40: 222-228.
57. Green AE, Hearmon RFS (1945) The buckling of flat rectangular plywood plates. Philosophical Magazine 36: 659-687.
58. Whitney JM (1970) Effect of boundary conditions on the response of laminated composites. Journal of Composite Materials 4: 192-203.
59. Whitney JM (1971) Fourier analysis of clamped anisotropic plates. ASME J Appl Mech 38: 530-532.
60. Whitney JM, Leissa AW (1970) Analysis of a simply supported laminated anisotropic rectangular plate. AIAA Journal 8: 28-33.
61. Kabir HRH, Khaleefi AM, Chaudhuri RA (2001) Free vibration analysis of thin arbitrarily laminated anisotropic plates using boundary-continuous displacement Fourier approach. Composite Structures 53: 469-476.
62. Chaudhuri RA, Balaraman K, Kunukkasseril VX (2005) A combined theoretical and experimental investigation on free vibration of thin symmetrically laminated anisotropic plates. Composite Structures 67: 85-97.
63. Hoff NJ, Rehfield LW (1965) Buckling of axially compressed circular cylindrical shells at stresses smaller than the classical critical value. ASME J Appl Mech 32: 542-546.
64. Kabir HRH, Chaudhuri RA (1993) A direct Fourier approach for analysis of thin finite-dimensional cylindrical panels. Computers & Structures 46: 279-287.
65. Chaudhuri RA, Kabir HRH (1994) Static and dynamic Fourier analysis of finite cross-ply doubly curved panels using classical shallow shell theories. Composite Structures 28: 73-91.
66. Chaudhuri RA, Kabir HRH (1993) Boundary-discontinuous Fourier analysis of doubly-curved panels using classical shallow shell theories. Int J Eng Sci 31: 1551-1564.
67. Chaudhuri RA, Kabir HRH (1992) A boundary-continuous-displacement based Fourier analysis of laminated doubly-curved panels using classical shallow shell theories. International J Eng Sci 30: 1647-1664.
68. Chaudhuri RA, Kabir HRH (1993) A boundary discontinuous Fourier solution for clamped transversely isotropic (pyrolytic graphite) Mindlin plates. Int J Solids and Struct 30: 287-297.
69. Kabir HRH, Chaudhuri RA (1992) Boundary-continuous Fourier solution for clamped Mindlin plates. ASCE J Eng Mech 118: 1457-1467.
70. Chaudhuri RA (1993) Closure to "Boundary Continuous Fourier Solution for Clamped Mindlin Plates" by Humayun R H Kabir and Reaz A Chaudhuri (July, 1992, Vol. 118, No. 7), ASCE J Eng Mech 119: 2364-2366.
71. Kabir HRH, Chaudhuri RA (1991) A generalized Navier's approach for solution of clamped moderately-thick cross-ply plates. Composite Structures 17: 351-366.
72. Chaudhuri RA, Kabir HRH (1992) Influence of laminations and boundary conditions on the response of moderately thick cross-ply rectangular plates. J Compos Mater 26: 51-77.
73. Chaudhuri RA, Kabir HRH (1992) Fourier analysis of clamped moderately thick arbitrarily laminated plates. AIAA Journal 30: 2796-2798.
74. Chaudhuri RA, Kabir HRH (1993) Vibration of clamped moderately thick general cross-ply plates using a generalized Navier's approach. Composite Structures 24: 311-321.
75. Chaudhuri RA, Kabir HRH (1994) Effect of boundary constraint on the frequency response of moderately thick flat laminated panels. Composites Engineering 4: 417-428.
76. Kabir HRH, Chaudhuri RA (1994) Vibration of clamped moderately thick arbitrarily laminated plates using a generalized Navier's approach. J Sound and Vib 171: 397-410.
77. Chaudhuri RA, Abu-Arja KR (1988) Exact solution of shear-flexible doubly curved anti-symmetric angle-ply shells. Int J Eng Sci 26: 587-604.
78. Chaudhuri RA, Abu-Arja KR (1991) Static analysis of moderately-thick finite anti-symmetric angle-ply cylindrical panels and shells. International Journal of Solids and Structures 28: 1-15.
79. Chaudhuri RA, Kabir HRH (1989) On analytical solutions to boundary-value problems of doubly-curved moderately-thick orthotropic shells. Int J Eng Sci 27: 1325-1336.
80. Chaudhuri RA, Kabir HRH (1993) Sensitivity of the response of moderately thick cross-ply doubly-curved panels to lamination and boundary constraint, part-I: theory. Int J Solids and Struct 30: 263-272.
81. Kabir HRH, Chaudhuri RA (1991) Free vibrations of shear-flexible anti-symmetric angle-ply doubly curved panels. Int J Solids and Struct 28: 17-32.
82. Kabir HRH, Chaudhuri R (1994) On Gibbs-phenomenon-free Fourier solution for finite shear-flexible laminated clamped curved panels. Int J Eng Sci 32: 501-520.
83. Kabir HRH, Khaleefi AM, Chaudhuri RA (2003) Frequency response of a moderately thick anti-symmetric cross-ply cylindrical panel with mixed type of Fourier solution functions. Journal of Sound and Vibration 259: 809-826.
84. Chaudhuri RA, Kabir HRH (2005) Effect of boundary constraint on the frequency response of moderately thick doubly curved cross-ply panels using mixed Fourier solution functions. Journal of Sound and Vibration 283: 263-293.
85. Basset AB (1890) On the extension and flexure of cylindrical and spherical thin elastic shells. Philosophical Transactions of the Royal Society of London A 181: 433-480.
86. Chaudhuri RA, Kabir HRH (1995) Fourier solution to higher-order theory based laminated shell boundary-value problem. AIAA Journal 33: 1681-1688.
87. Giunta G, Biscani F, Belouettar S, et al. (2011) Hierarchical modelling of doubly curved laminated composite shells under distributed and localized loadings. Composites B 42: 682-691.
88. Chaudhuri RA, Oktem AS (2020) Flattening effect of negative Gaussian curvature on simply-supported thick asymmetric cross-ply panels in absence of surface-parallel edge restraints. ASCE J Aerospace Engineering 33.
89. Chaudhuri RA, Oktem AS (2022) Cylindrical-panel-like response of fully surface-parallel restrained simply supported hyperbolic-paraboloidal thick general cross-ply panels. Journal of Aerospace Engineering and Mechanics (in review).
90. Mantari JL, Oktem AS, Guedes Soares C (2012) A new trigonometric shear deformation theory for isotropic, laminated composite and sandwich plates. International Journal of Solids and Structures 49: 43-53.
91. Xavier PB, Chew CH, Lee KH (1995) Buckling and vibration of multilayer orthotropic composite shells using a simple higher-order layer wise theory. Int J Solids Struct 32: 3479-3497.
92. Librescu L, Khedir AA (1988) Analysis of symmetric cross-ply laminated elastic plates using a higher-order theory: part I - stress and displacement. Compos Struct 9: 189-213.
93. Oktem AS, Chaudhuri RA (2007) Levy type analysis of cross-ply plates based on higher-order theory. Composite Structures 78: 243-253.
94. Oktem AS, Chaudhuri RA (2007) Fourier solution to a thick Levy type clamped plate problem. Composite Structures 79: 481-492.
95. Oktem AS, Chaudhuri RA (2007) Levy type Fourier analysis of thick cross-ply doubly-curved panels. Composite Structures 80: 475-488.
96. Oktem AS, Chaudhuri RA (2007) Fourier analysis of thick cross-ply Levy type clamped doubly-curved panels. Composite Structures 80: 489-503.
97. Chaudhuri RA, Oktem AS, Guedes Soares C (2015) Levy-type boundary Fourier analysis of thick clamped hyperbolic-paraboloidal cross-ply panels. AIAA Journal 53: 140-149.
98. Chaudhuri RA, Oktem AS, Guedes Soares C (2015) Levy-type boundary Fourier analysis of thick cross-ply panels with negative Gaussian curvature. AIAA Journal 53: 2492-2503.
99. Oktem AS, Chaudhuri RA (2007) Boundary discontinuous Fourier analysis of thick cross-ply clamped plates. Composite Structures 82: 539-548.
100. Oktem AS, Chaudhuri RA (2008) Effect of in plane boundary constraints on the response of thick general (unsymmetric) cross-ply plates. Composite Structures 83: 1-12.
101. Oktem AS, Chaudhuri RA (2009) Higher-order theory based boundary-discontinuous Fourier analysis of simply supported thick cross-ply doubly curved panels. Composite Structures 89: 448-458.
102. Oktem AS, Chaudhuri RA (2009) Sensitivity of the response of thick doubly curved cross-ply panels to edge clamping. Composite Structures 87: 293-306.
103. Oktem AS, Guedes Soares C (2012) Higher order theory based Fourier analysis of cross-ply plates and doubly curved panels. J Compos Mater 46: 2675-2694.
104. Chaudhuri RA, Oktem AS (2016) Analysis of simply-supported saddle-shaped symmetric cross-ply panels with no surface-parallel boundary constraints. AIAA Journal 54: 782-788.
105. Chaudhuri RA, Oktem AS (2016) Simply-supported saddle-shaped thick symmetric cross-ply panels: full surface-parallel boundary constraints. AIAA Journal 54: 2194-2199.
106. Chaudhuri RA, Balaraman K (2007) A novel method for fabrication of fiber reinforced plastic laminated plates. Composite Structures 77: 160-170.
107. Qi WK, Cheng B, Liu L (2013) Research of vibration modal experiment for composite laminates. Aeroengine 39: 53-58.
108. Li H, Chang Y, Xu Z, et al. (2018) Modal shape measurement of fiber-reinforced composite plate with high efficiency and precision based on laser linear scanning method. Measurement and Control 51: 470-487.
109. Jones RM (1999) Mechanics of Composite Materials, (2nd edition), Taylor and Francis.
110. Chaudhuri RA (2005) Analysis of laminated shear-flexible angle-ply plates. Composite Structures 67: 71-84.
111. Chaudhuri RA, Seide P (1987) Triangular finite element for analysis of thick laminated plates. Inter J Numer Methods Eng 24: 1203-1224.
112. Carrera E (2003) Historical review of zig-zag theories for multilayered plates and shells. Applied Mechanics Reviews 56: 287-308.
113. Seide P, Chaudhuri RA (1987) Triangular finite element for analysis of thick laminated shells. Int J Numer Methods Eng 24: 1563-1579.
114. Chaudhuri RA (2009) A new three-dimensional shell theory in general (non-lines of curvature) coordinates for analysis of curved panels weakened by through/part-through holes. Composite Structures 89: 321-332.
115. Chaudhuri RA, Kabir HRH (1993) Sensitivity of the response of moderately thick cross-ply doubly-curved panels to lamination and boundary constraint, part - II: application. Inter J Solids and Struct 30: 273-286.
116. Chaudhuri RA (2010) A micro-kink theory for determination of shear modulus of a unidirectional composite lamina. Composite Structures 92: 395-400.
117. Chaudhuri SN, Chaudhuri RA, Benner RE (2006) Raman spectroscopy for characterization of interfacial debonds between carbon fibers and polymer matrices. Composite Structures 76: 375-387.
118. Chaudhuri RA, Abu-Arja KR (1986) Plastic deformation of a boron/aluminum tube under multi-axial loadings. Computers & Structures 24: 915-921.
119. Paul B (1963) Linear bending theory of laminated cylindrical shells under axisymmetric load. ASME J Appl Mech 30: 98-102.
120. Chaudhuri RA, Balaraman K, Kunukkasseril VX (1986) Arbitrarily laminated anisotropic cylindrical shells under internal pressure. AIAA Journal 24: 1851-1858.
121. Chaudhuri RA, Balaraman K, Kunukkasseril VX (2008) Admissible boundary conditions and solutions to internally pressurized thin arbitrarily laminated cylindrical shell boundary-value problems. Composite Structures 86: 385-400.
122. Chaudhuri RA Oktem AS Guedes Soares C (2013) Internally pressurized thin cross-ply cantilever cylindrical shells. AIAA Journal 51: 2523-2526.
123. Chaudhuri RA, Oktem AS, Guedes Soares C (2015) Beam-column and tie-bar effects in internally pressurized thin arbitrarily laminated cantilever cylindrical shells. ASCE J Eng Mech ASCE 141: 04014131.
124. Abu-Arja KR, Chaudhuri RA (1989) Influence of transverse shear deformation on the scaling of cross-ply cylindrical shells. Journal of Composite Materials 23: 673-694.
125. Abu-Arja KR, Chaudhuri RA (1989) Moderately thick angle-ply cylindrical shells under internal pressure. ASME Journal of Applied Mechanics 56: 652-657.
126. Chaudhuri RA, Abu-Arja KR (1989) Closed-form solutions for arbitrarily laminated anisotropic cylindrical shells (tubes) including shear deformation. AIAA Journal 27: 1597-1605.
127. Kunukkasseril VX, Chaudhuri RA, Balaraman K (1975) A method to determine eighteen rigidities of layered anisotropic plates. Fibre Science and Technology 8: 303-318.
128. Whitcomb JD, Raju IS, Goree JG (1982) Reliability of the finite element method for calculating free edge stresses in composite laminates. Computers & Structures 15: 23-27.
129. Chaudhuri RA, Seide P (1986) Triangular element for analysis of a stretched plate weakened by a part-through hole. Computers & Structures 24: 97-105.
130. Chaudhuri RA (2009) Computation of transverse shear stresses in the vicinity of the circumferential re-entrant corner line of an internal part-through hole weakening an edge-loaded plate. Composite Structures 89: 315-320.
131. Chaudhuri RA (2010) Transverse shear stress distribution through thickness near an internal part-through elliptical hole in a stretched plate. Composite Structures 92: 818-825.
132. Chaudhuri RA (2015) A combined FEM and three-dimensional asymptotic solution based analysis on stress concentration/intensity around elliptical/circular cylinder shaped surface flaws in stretched plates. Applied Mathematical Modelling 39: 5341-5353.
133. Chaudhuri RA (2007) Weakening effects of internal part-through elliptic holes in homogeneous and laminated composite plates. Composite Structures 81: 362-373.
134. Chaudhuri RA (1987) Stress concentration around a part-through hole weakening a laminated plate. Computers & Structures 27: 601-609.
135. Chaudhuri RA, Seide P (2010) Interlaminar shear stresses around an internal part-through hole in a laminated composite plate. Composite Structures 92: 835-843.
136. Chaudhuri RA, Seide P (2011) Interlaminar shear stresses around internal elliptical cylindrical holes weakening edge-loaded cross-ply plates. AIAA journal 49: 1292-1298.
137. Chaudhuri RA, Oktem AS, Guedes Soares C (2013) Stress concentration/intensity around elliptical/circular cylinder shaped surface flaws in cross-ply plates and validity of St. Venant's principle in the presence of interacting singularities. Appl Math Model 37: 1362-1377.