Journal of Fluid Dynamics

Effect of Nonlinear Thermal Radiation on MHD Flow over a Vertical Cylinder Moving with Nonlinear Velocity

Abstract

This paper discusses the effect of nonlinear radiative magnetohydrodynamic flow over a vertical cylinder that moves with nonlinear velocity. The mathematical model of the problem is constructed including different parameters such as the nonlinearity parameter, the thermal radiation parameter, the magnetic parameter, etc. Suitable similarity transformation is used to transform the system of partial differential equations that describes the fluid motion into a system of ordinary differential equations. The obtained system along with the associated boundary conditions is solved numerically using Mathematica. Such method is validated through comparing the results obtained with analytic solutions for some parameter values. Exhibiting the fluid velocity and temperature pro les in graphs enables to understand the effects of different parameters under consideration.

Keywords

MHD boundary layer flow, Moving cylinder, Nonlinear thermal radiation, Nonlinear velocity, Similarity solutions

Introduction

Due to the enormous industrial and engineering applications of the flow of Newtonian and Non-Newtonian fluids many authors devoted efforts to such studies, especially in the last few decades. The problem of our concern that is the boundary layer flow over a moving cylinder has many industrial applications such as plastic and metallurgy industries as well as wire drawings. Sakiadis [1] examined the behaviour of boundary layer flow on a moving continuous surface. Rotte and Beek [2] constructed an approximate solution to the case of cooling or heating a continuously moving cylinder. The effects of mass transfer and thermal radiation on the flow of a viscous incompressible fluid past a moving vertical cylinder was analyzed by Ganesan and loganathan [3]. Abo-Eldahab and Salem [4] have recently investigated the problem of flow past a moving cylinder while considering the heat transfer of non-Newtonian power-law fluid with diffusion and chemical reaction. The concept of Magnetohydrodynamic (MHD) arises when we consider the case of fluid flow in electrically conducting fluids whenever magnetic properties affect fluid flow characteristics. A current is induced upon a magnetic field is incident in an electrically conducting fluid. There are enormous industrial applications of MHD in technology such as the industry of Petroleum, plasma studies, designs of MHD power generator, and the design of nuclear reactors. The steady flow of an electrically conducting incompressible fluid past a semi-infinite moving vertical cylinder in the presence of a transverse magnetic field is investigated by Amkadni and Azzouzi [5]. Elbashbesh, et al., [6] presented the study of boundary layer flow over a horizontal stretching cylinder embedded in a porous medium. The study included the effects of thermal radiation, heat transfer, and suction/injection. Abdul Rehman, et al., [7] gave an analytic solution of the flow of a micropolar fluid past over a moving cylinder, in their study they took into consideration axisymmetric stagnation flow. A good view of the electrically conducting boundary layer flow of incompressible viscoelastic nanofluid that flows due to a moving linearly stretching surface can be found in the work of Haroon, et al., [8]. The references [9-15] give a good review for the recent studies of the boundary layer flow over a cylinder. In this paper, we study the problem of heat and mass transfer and MHD flow over a cylinder that moving vertically with nonlinear velocity under the action of a uniform magnetic field, in the presence of nonlinear thermal radiation. An analytic solution will be found for some special cases and numerical solution will be reached and the results will show the effects of different parameters considered here on the fluid velocity and fluid temperature.

Mathematical Model of the Problem

The study assumes an incompressible steady laminar flow over a semi-infinite cylinder of radius R that is moving nonlinearly. The coordinates are designed such that x is measured along the cylinder axis where r intersects with x axis at the origin and refers to the radial coordinate that is normal to the cylinder axis. The fluid properties are considered to be constant. A transverse magnetic field is applied and assumed to be uniform with strength B ₀ and the external velocity is considered as u _e ( x ) = u _∞ ( x/l ) ⁿ , u _∞ > 0. Such assumptions lead to the governing equations:

$$\frac{\partial (rv)}{\partial r}+\frac{\partial (ru)}{\partial x}=0\text{ (2}\text{.1)}$$

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}=\frac{v}{r}\frac{\partial }{\partial r}(r\frac{\partial u}{\partial r})+u_e\frac{d{u}_e}{dx}+\frac{\sigma B_0{}^2}{\rho }(u_e-u)\text{ (2}\text{.2)}$$

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial r}=\frac{\alpha }{r}[\frac{\partial }{\partial r}(r\frac{\partial T}{\partial r})-\frac{1}{k}\frac{\partial }{\partial r}(r{q}_r)]\text{ (2}\text{.3)}$$

along with the boundary conditions:

$$u(R,x)=u_w{(\frac{x}{l})}^n,v(R,x)=0,\underset{r\to \infty }{\lim }u(r,x)=u_{\infty }{(\frac{x}{l})}^n\text{ (2}\text{.4)}$$

$$T(R,x)=T_w,\underset{r\to \infty }{\lim }T(r,x)=T_{\infty }\text{ (2}\text{.5)}$$

Where u and v represent the velocity components along the x and r directions respectively, ν stands for the kinematic viscosity, ρ is the density of the fluid, σ is the fluid electrical conductivity, l is taken as the characteristic length, B ₀ is the magnetic field intensity, α is the thermal diffusivity, κ is the thermal conductivity, and $q_r=\frac{-4{\alpha }^{*}}{3k^{*}}\frac{\partial T^4}{\partial r}$ is the radiation heat flux in the radial direction, σ ^∗ is the Stefan-Boltzmann constant and k ^∗ is the Rosseland radiation absorptivity.

A stream function ψ is defined as:

$$ru=\frac{\partial \Psi }{\partial r},rv=-\frac{\partial \Psi }{\partial x}\text{ (2}\text{.6)}$$

Where,

$$\Psi =\sqrt{\frac{vR(n+1)u_{\infty }}{2}{(\frac{x}{l})}^{n+1}Rf(\eta )},\eta =\sqrt{\frac{u_{\infty }}{2vR(n+1)}{(\frac{x}{l})}^{n-1}\frac{1}{R}(r^2-R^2)}\text{ (2}\text{.7)}$$

Where f is the dimensionless stream function and η is the dimensionless similarity variable. Defining the dimensionless temperature as:

$$\theta (\eta )=\frac{T-T_{\infty }}{T_w-T_{\infty }}\text{ (2}\text{.8)}$$

The governing equations and boundary conditions thus take the form:

$$\frac{2}{n+1}(\eta K+1)f^{‴}+(\frac{2K}{n+1}+\frac{\epsilon (n+1)}{2}f)f^{″}+n\epsilon (1-{(f^{\prime })}^2)-M(f^{\prime }-1)=0\text{ (2}\text{.9)}$$

$$\frac{\in {(n+1)}^2{P}_r}{4K}f{\theta }^{\prime }+(1+R_d{(1+({\theta }_w-1)\theta )}^3){\theta }^{\prime }+(\{1+R_d(1+({\theta }_w-1){\theta }^3\}C{\theta }^{\prime }{)}^{\prime }=0\text{ (2}\text{.10)}$$

Where $K=\sqrt{\frac{2v(n+1)}{u_{\infty }R}{(\frac{l}{x})}^{n-1}},\in =\frac{R}{l},$ the magnetic parameter $M=\frac{\sigma B_0^{2}R}{\rho u_{\infty }}{(\frac{l}{x})}^{n-1},$ P _r is the Prandtl number, the thermal radiation parameter $R_d=\frac{16{\sigma }^8{T}_{\infty }^3}{3K^8\kappa },{\theta }_w=\frac{T_w}{T_{\infty }},C=\frac{r^2}{M{R}^2}$ . The boundary conditions take the form

$$f(0)=0,f^{\prime }(0)=\frac{u_w}{u_{\infty }}=a,f^{\prime }(\infty )=1,\theta (0)=1,\theta (\infty )=0$$

To solve the system (9)-(11) numerically we transform it into a system of first order ordinary differential equations as follows: y ₁ ( η ) = f ( η ) , y ₂ ( η ) = f ^′ ( η ) , y ₃ ( η ) = f ^′′ ( η ) , y ₄ ( η ) = θ ( η ) , y ₅ ( η ) = θ ^′ ( η ) to get the system

$$y_1{}^{\prime }=y_2\text{ (2}\text{.12)}$$

$$y_2{}^{\prime }=y_3\frac{2}{n+1}(\eta K+1)y_3{}^{\prime }=-(\frac{2K}{n+1}+\frac{\epsilon (n+1)}{2}{y}_1)y_3-\eta \in (1-y_2{}^2)+M(y_2-1)\text{ (2}\text{.13)}$$

$$y_4{}^{\prime }=y_5\text{ (2}\text{.14)}$$

$$(\{1+R_d(1+({\theta }_w-1)y_4{}^3\}C{y}_5{)}^{\prime }=-(1+R_d(1+({\theta }_w-1)y_4{}^3)y_5-\frac{\in {(n+1)}^2{\mathrm{P}}_r}{4K}{y}_1{y}_5\text{ (2}\text{.15)}$$

subject to the initial conditions:

$$y_1(0)=0,y_2(0)=a,y_3(0)=s,y_4(0)=1,y_5(0)=u\text{ (2}\text{.16)}$$

The numerical values of the parameters are chosen in a suitable way. The values of s and u are priori unknown and are determined as a part of the solution. While the parameters numerical values are assigned according to the problem physics.

Method of Solutions

The mathematical model of the problem is solved numerically using MATHEMATICA through defining a function F [ s _ ,u _]:= NDSolve [12-17]. The numerical values of s and u are determined through solving the equations y ₂ ( η _m ax ) = 1, y ₄ ( η _m ax ) = 0. A reasonable start value is assigned to η _m ax and hence increased till we nd η _m ax for which the difference between two successive values of s and those of u are less than 10 ⁷ . Once ( η _m ax ) s and u are determined, the problem can be solved easily as an initial value problem using the Mathematica function NDSolve. See references [15] and [16]. To ensure the validity of the numerical method used in this work, consider equation (9) in case of n = 1.

$$(\eta K+1)f^{‴}+(K+\epsilon f)f^{″}+\epsilon (1-{f^{\prime }}^2)-M(f^{\prime }-1)=0\text{ (3}\text{.1)}$$

with the boundary conditions:

$$f(0)=0,f^{\prime }(0)=\frac{u_w}{u_{\infty }}=a,f^{\prime }(\infty )=1\text{ (3}\text{.2)}$$

Where $K=\sqrt{\frac{4v}{u_{\infty }R}}$ and $M=\frac{\sigma B^2{}_{0}R}{\rho u_{\infty }}$ .

The exact solution given in ref [16] is:

$$f(\eta )=\eta +\frac{(a-1)K}{\epsilon }(1-e^{\frac{-\in \eta }{K}})\text{ (3}\text{.3)}$$

Here we give a comparison between the numerical solutions of equations (18) and (19) using the numerical method presented in this work and the exact solutions given by equation (20) for some special cases. Such comparison is elucidated in Table 1 which presents a comparison of f ^′′ (0) for K = 0 . 3 and ϵ = 1. Column 4 of Table 1 gives the numerical calculated values of |f ^′′ (0) − 1|. Exact values should be zeroes as η _m ax → ∞ . Results shown in Table 1 assure the validity of the numerical method presented in this work.

Results and Discussions

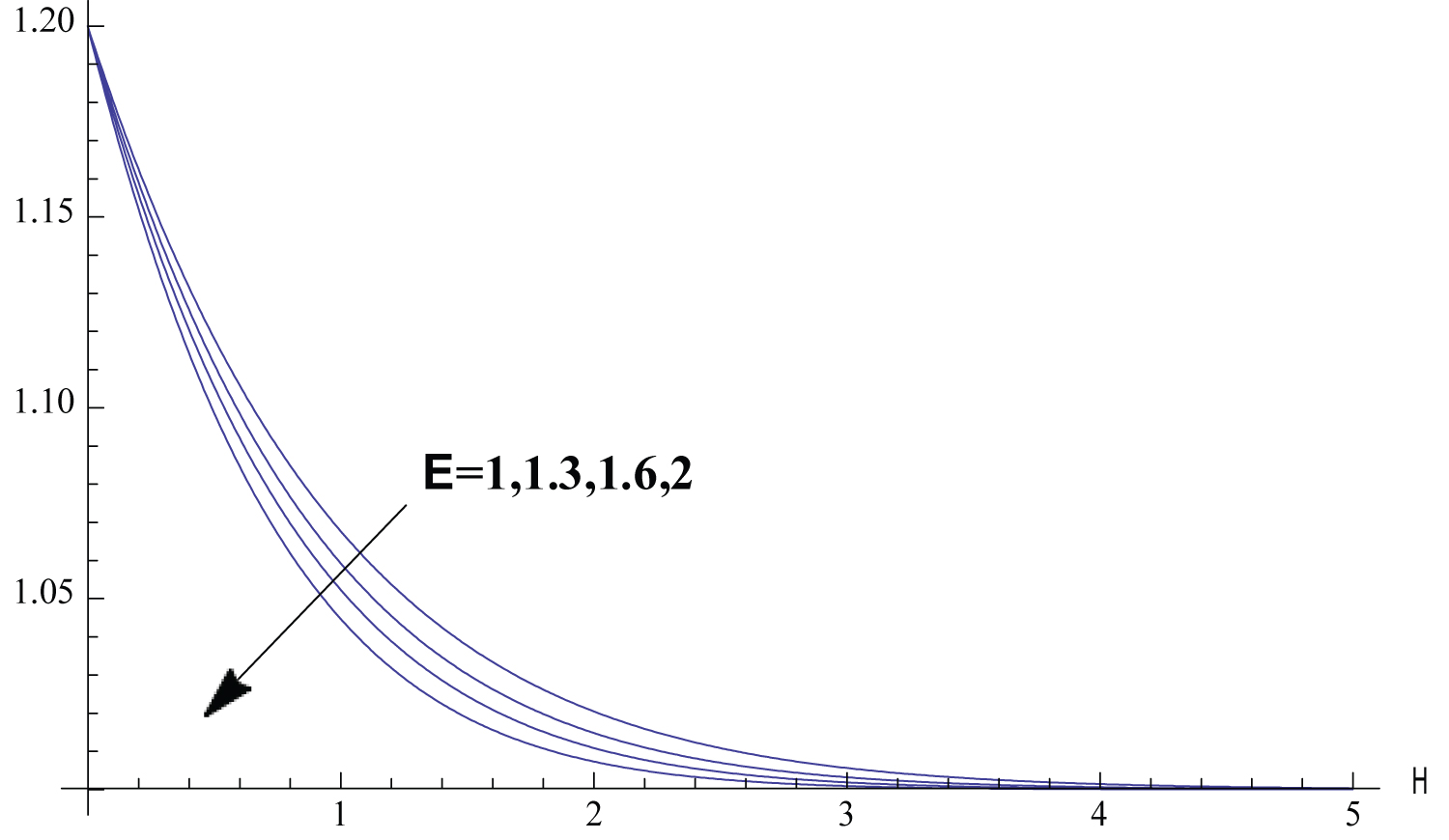
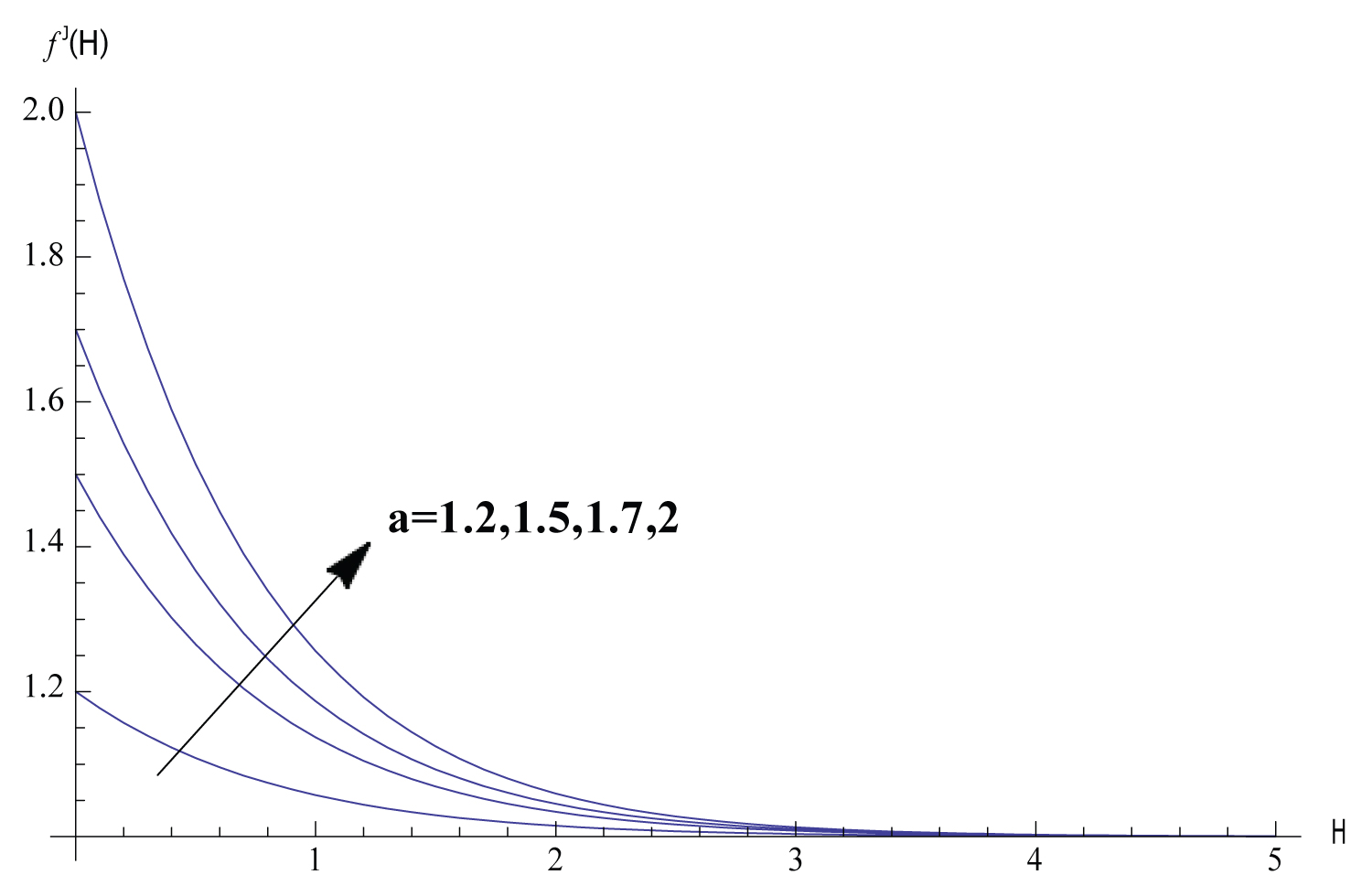
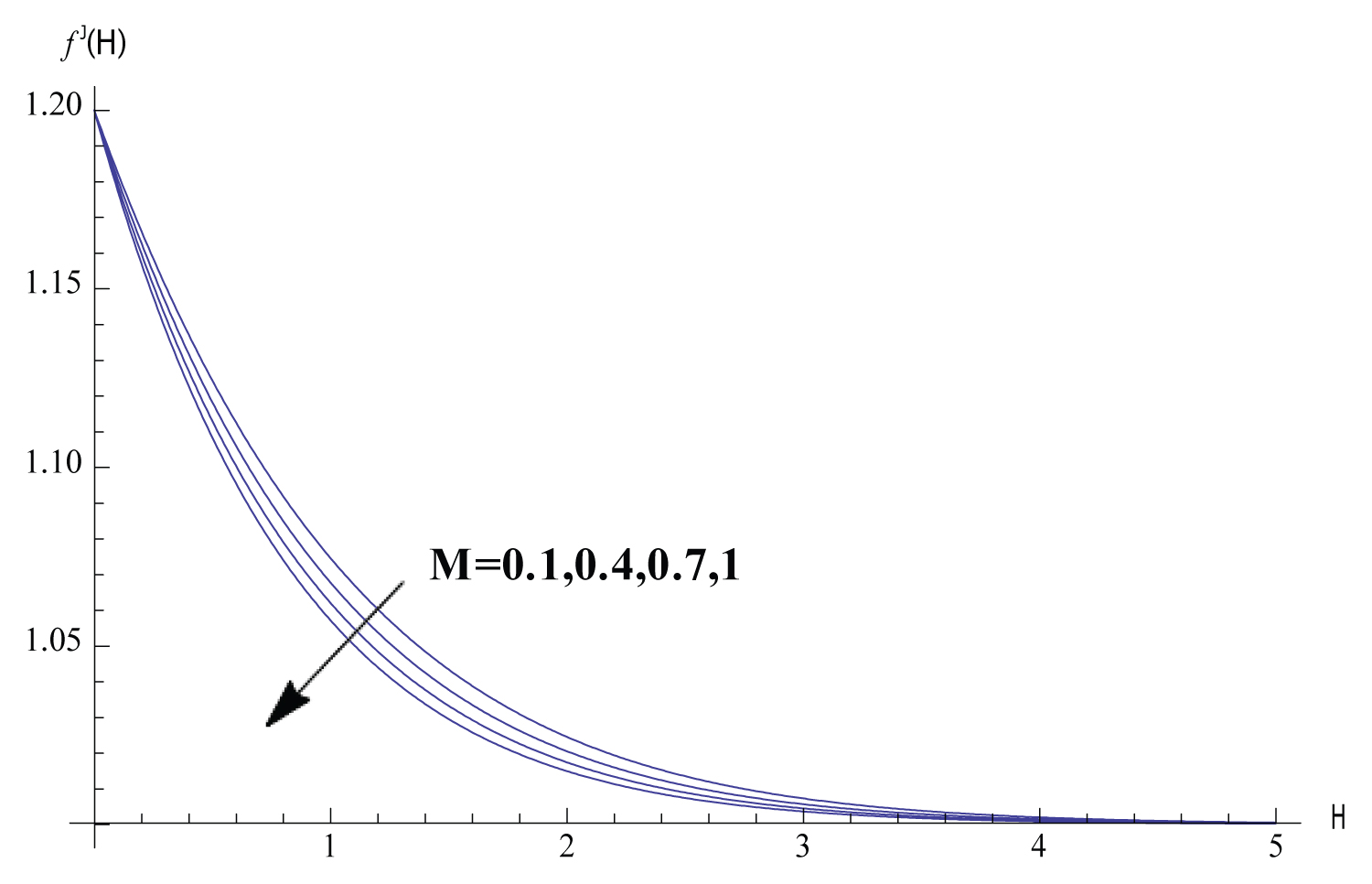
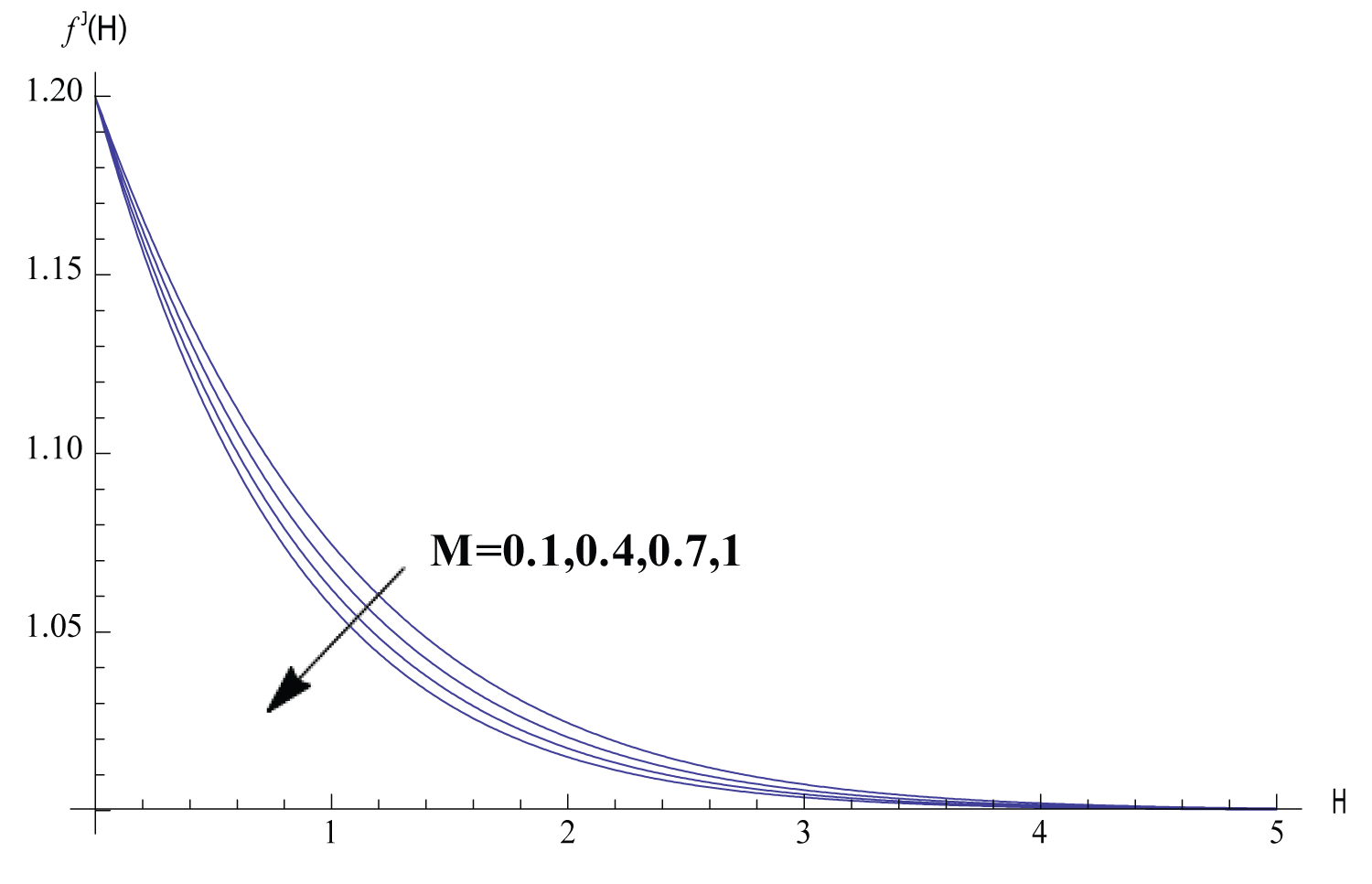
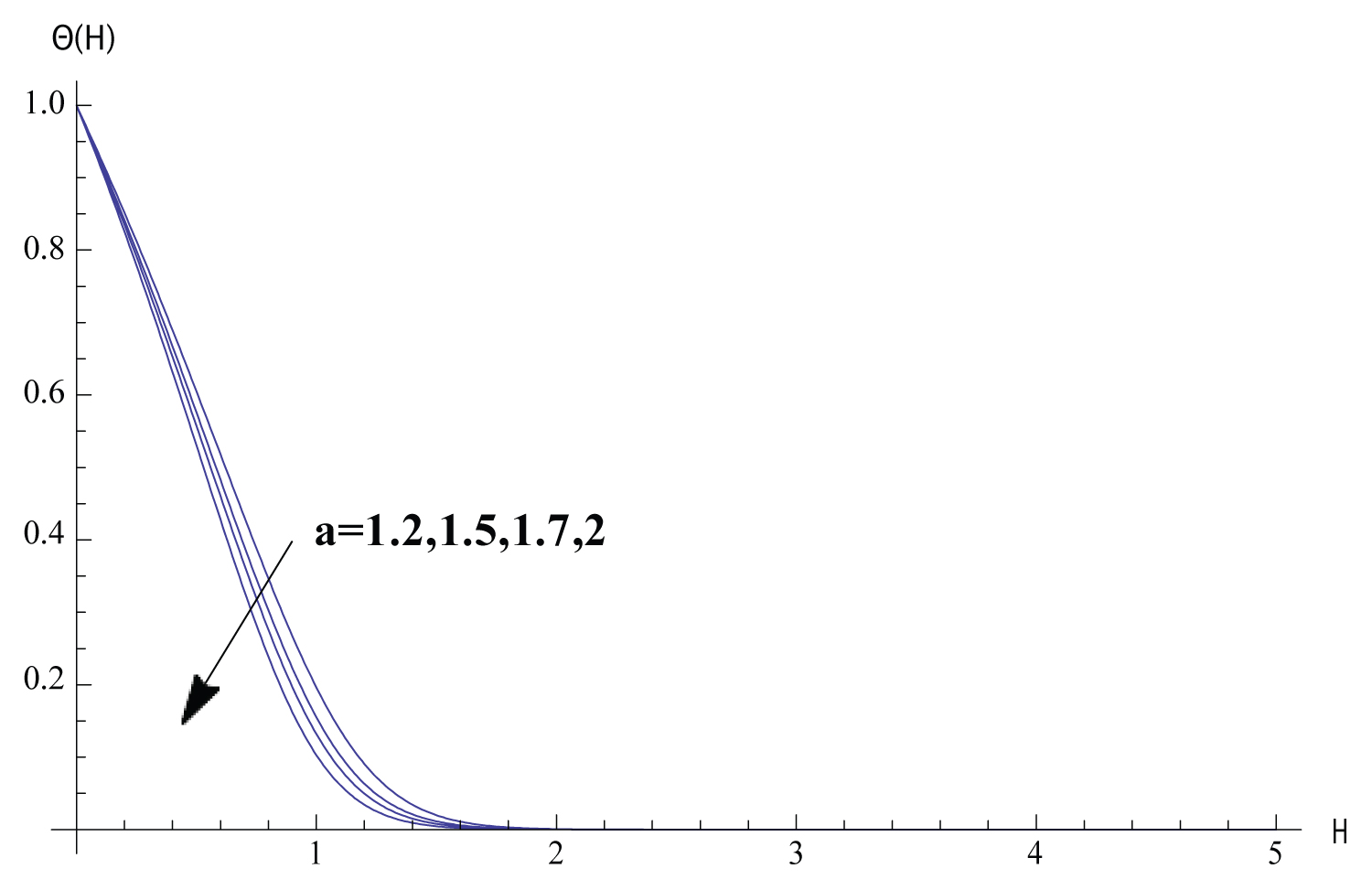
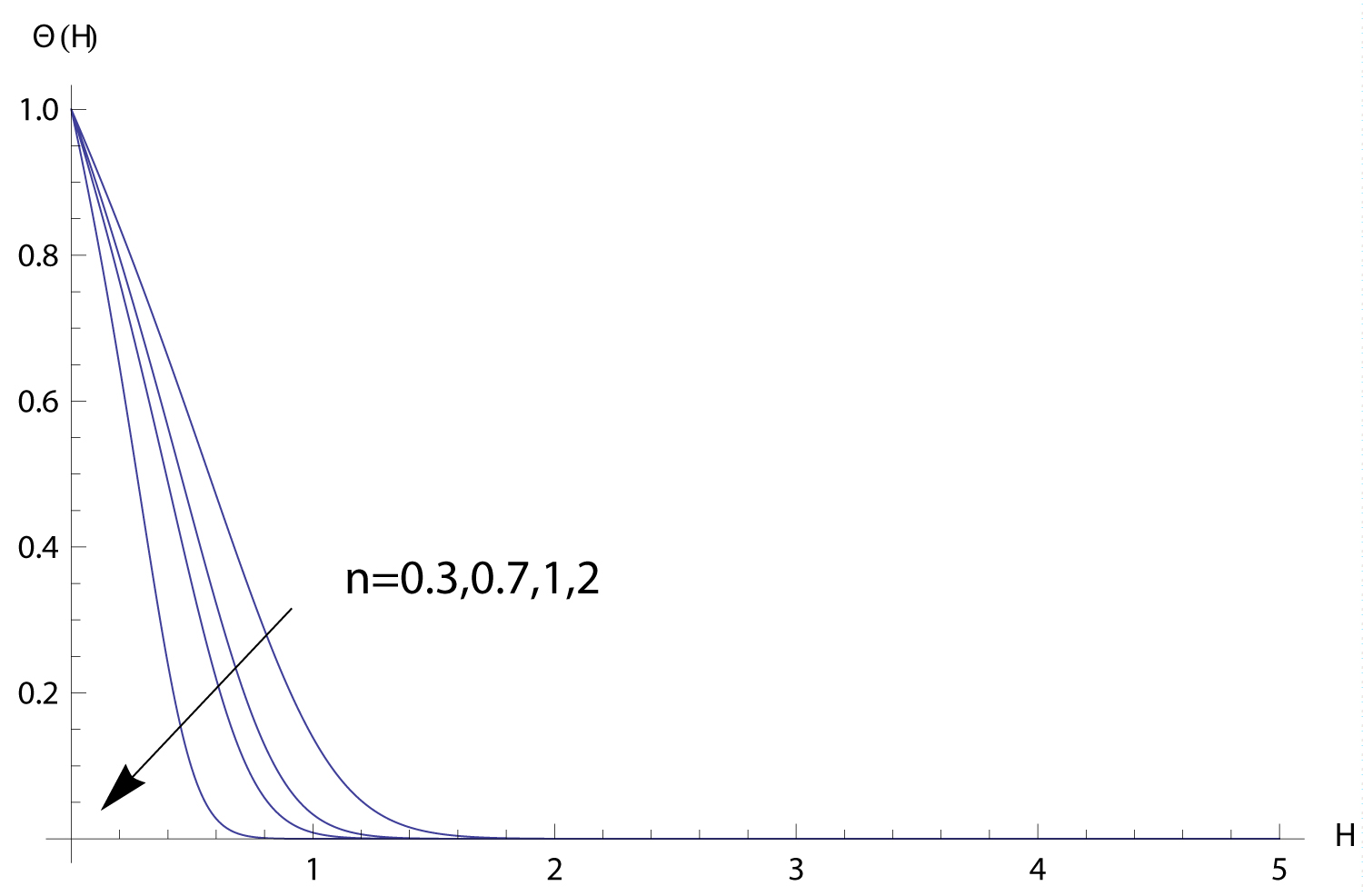
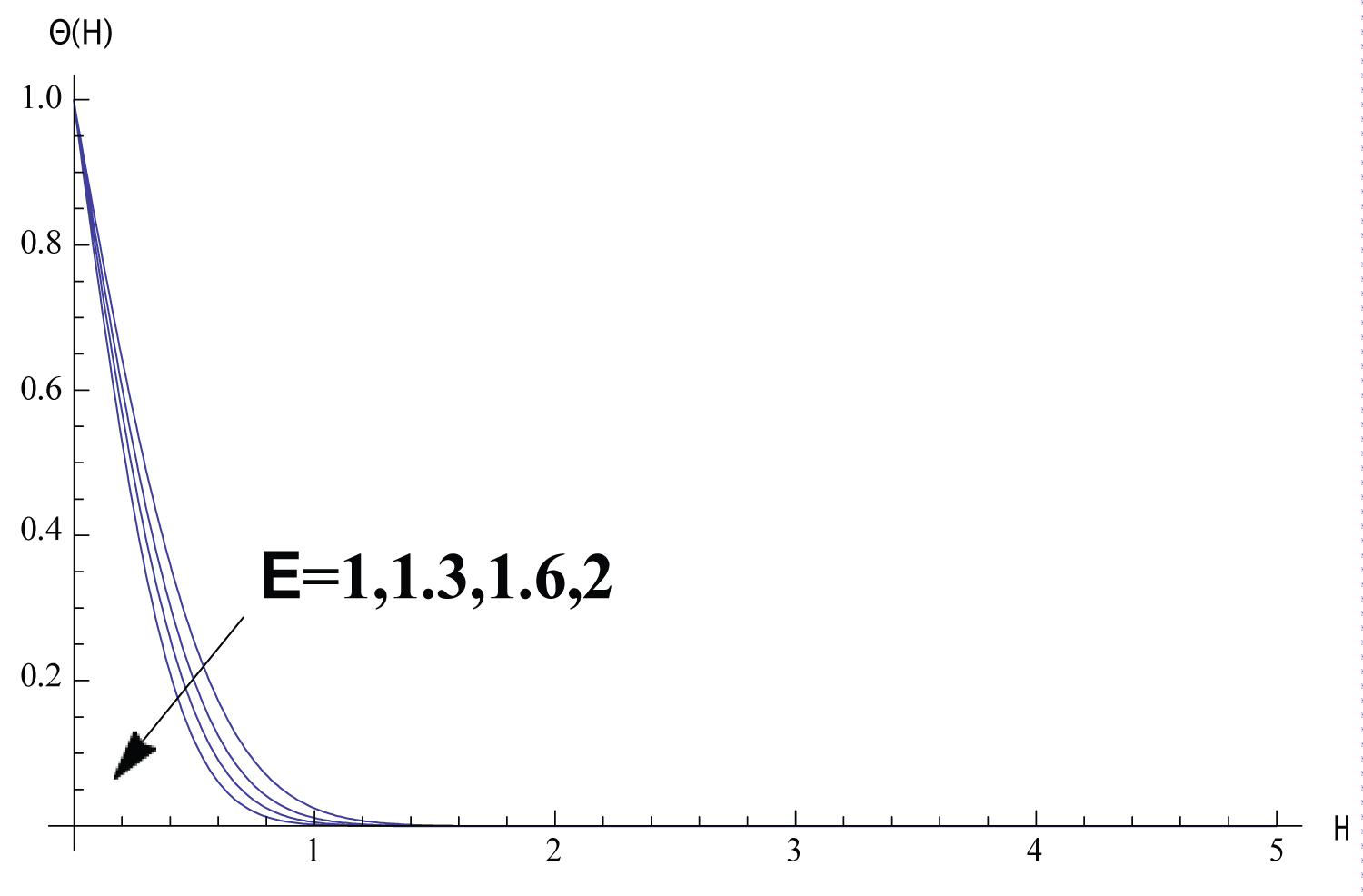
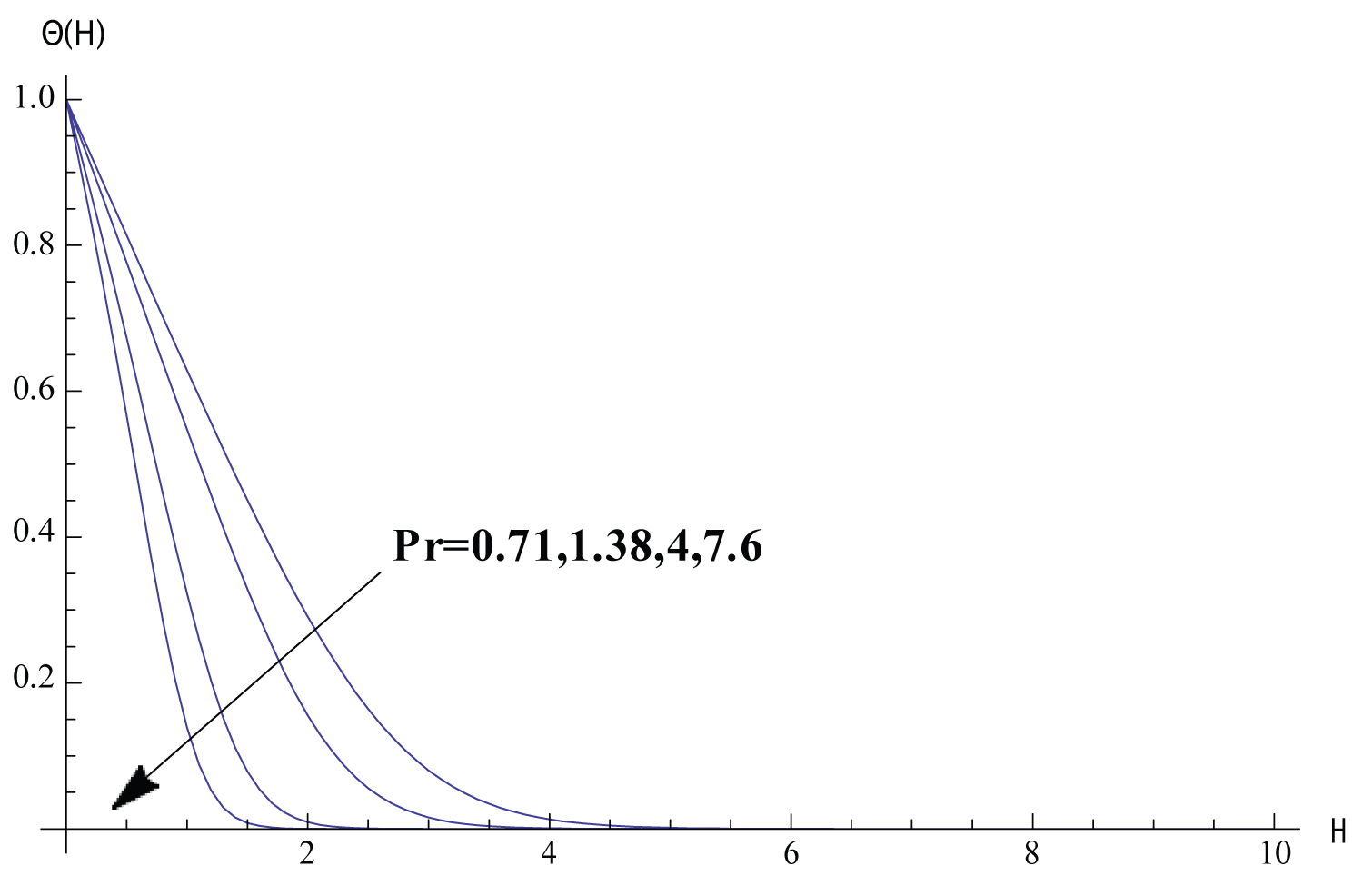
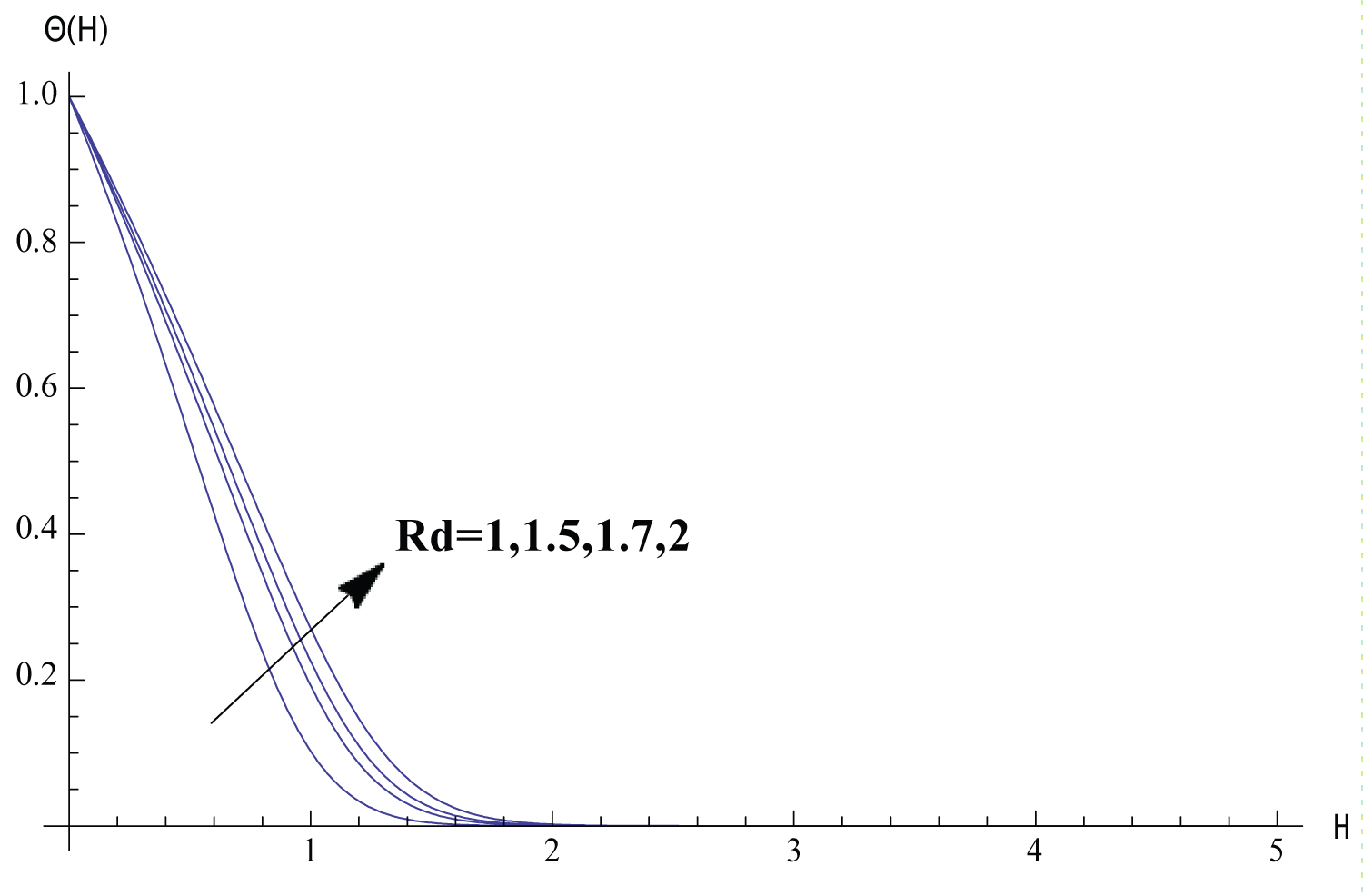
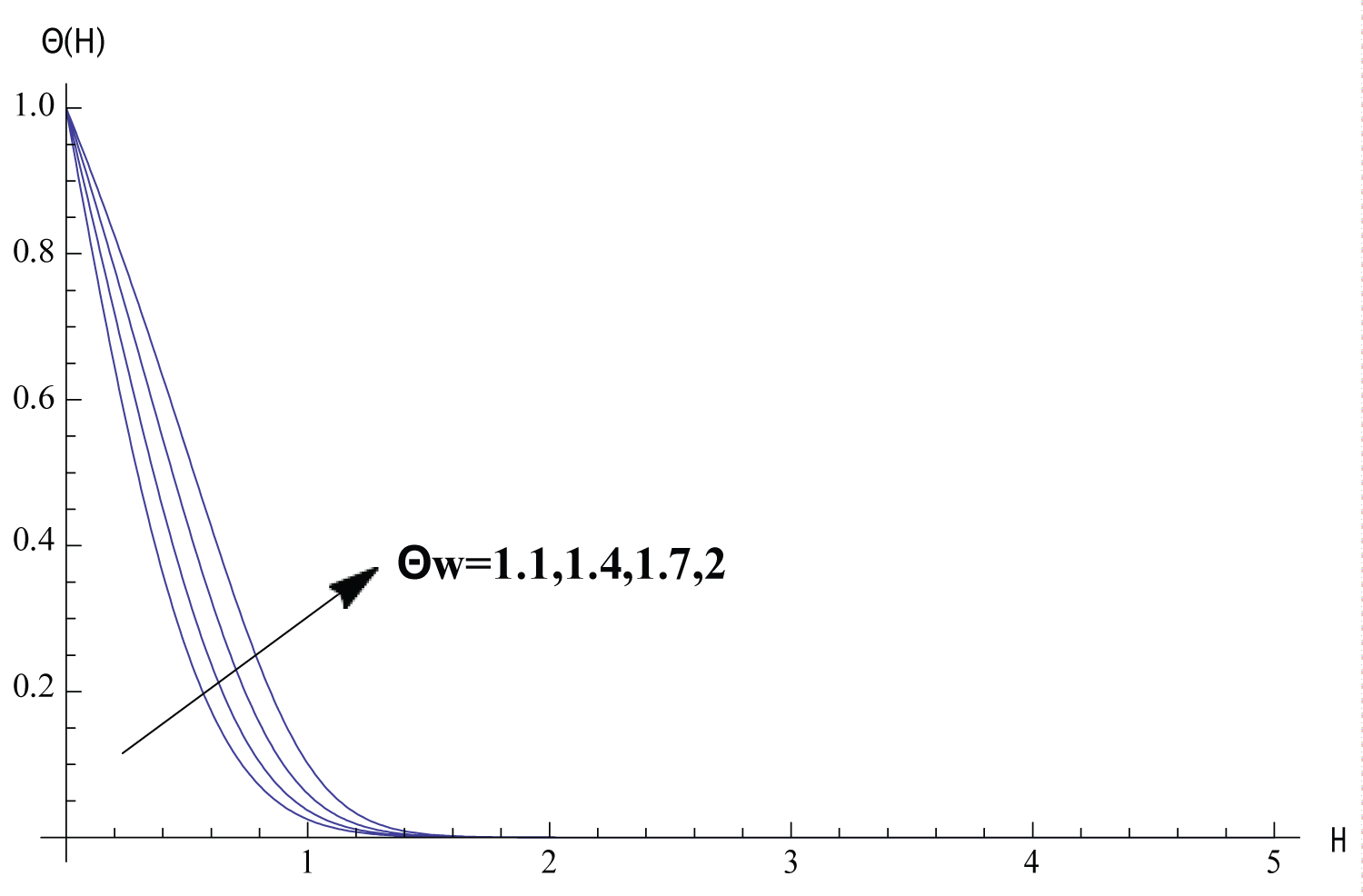
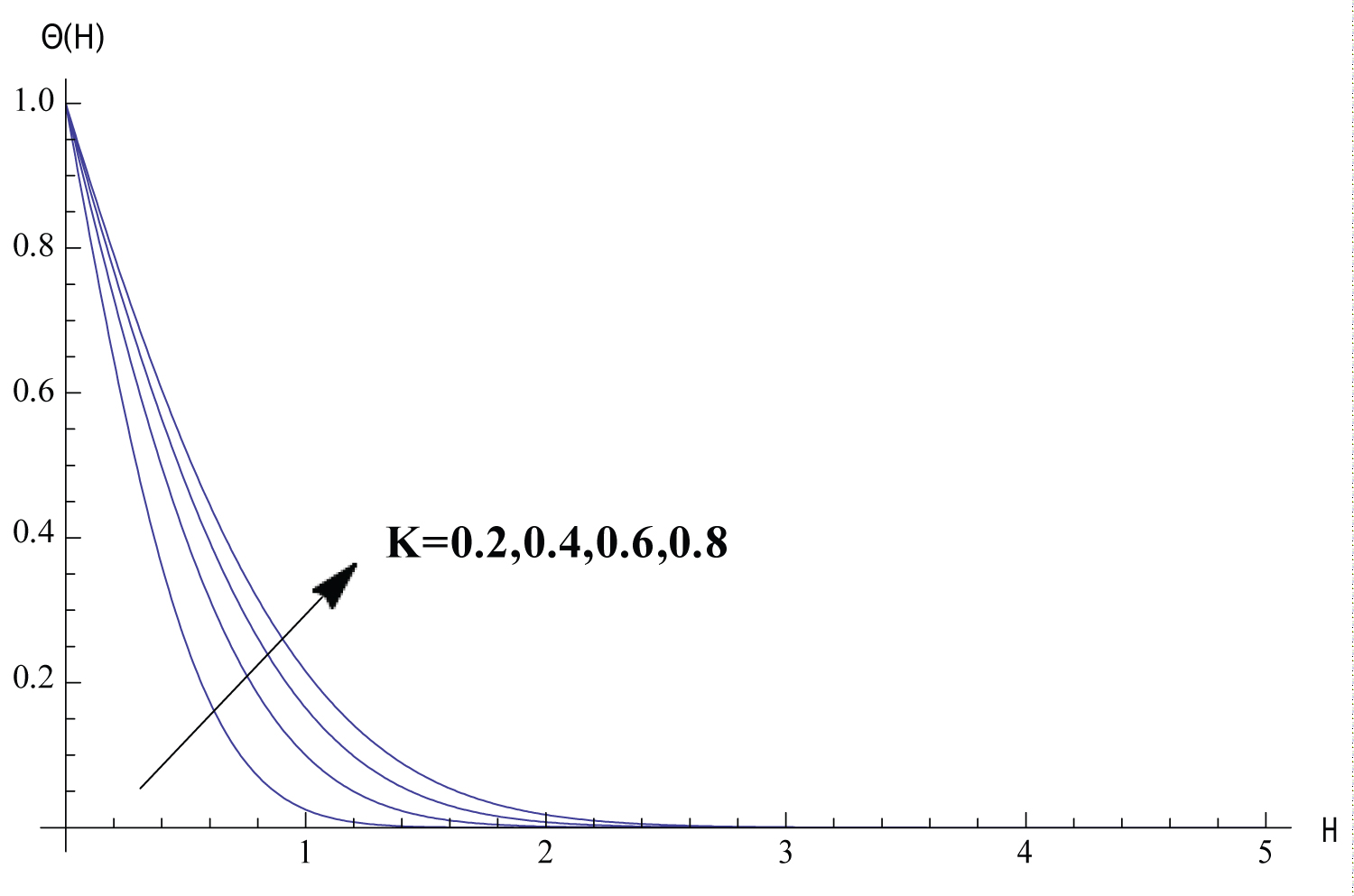
In this section, Solutions of the problem is given for different values of the parameters. We study the variance of the fluid velocity f ′(η) and the temperature of the fluid θ(η) with the similarity variable η for different reasonable values of the parameters governing the fluid motion. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 exhibits how the fluid velocity varies with the similarity variable η. The velocity of the fluid changes inversely with η till the velocity becomes one which refers to the case of ambient fluid. Figure 1 shows the fluid velocity is affected by changing the parameter . The fluid velocity decreases as ϵ increases. In fact the increase of $\in =\frac{R}{l}$ results in decreasing the cylinder surface area. Shrinking the surface area of the cylinder evolves to the increase of the space provided to the free stream velocity which enhances the tendency of the fluid velocity to get the value of the free stream velocity. Figure 2 elucidate the effect of the parameter n on the fluid velocity. The increase of n results in slowing the fluid. Such inverse relation can be understood through investigating the values of f ^′′ (0) for different values of n which is shown in Table 2 proving that f ^′′ (0) decreases with the increase of n which implies the effect of n on the fluid velocity. The fact that increasing the initial velocity of the fluid gives rise to accelerating the fluid is ensured in Figure 3. The value of - f ^′′ (0) and consequently the skin friction coefficient increases as the magnetic parameter M increases as shown in Table 2. Such direct relation enhances the slowing of the fluid as noticed in Figure 4. Figure 5 shows that the fluid velocity decreases with the increase of the value of the parameter K. The justification of this behaviour is that - f ^{′ ′} (0) increases with the increase of K as shown in Table 2. The variations of the fluid temperature similarity variable θ(η) that is the difference between the temperature of the fluid and the ambient temperature with η are elucidated in Figures 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12. The value of θ(η) decreases as η increases damping to zero which is already expected since as increasing η the fluid temperature gets closer to the ambient temperature value. Figure 6 elucidates the fact that as the initial velocity increases the fluid velocity increases also and consequently the cooling rate evolves which gives rise to decreasing the fluid temperature θ(η). The effect of the variation of the parameter n on the fluid temperature is elucidated in Figure 7. Increasing the value of n results in a decrease of the fluid temperature θ(η) since the increase of n implies an increase of the surface heat ux -θ ^′ (0) as exhibited in Table 2. Figure 8 exhibits the variation of fluid temperature with the parameter ϵ. The inverse relation between θ and  is a result of the fact that as the cylinder radius increases the cylinder surface area increases which consequently increases the value of -θ ^′ (0) and so the fluid temperature decreases. The variation of the Prndtle number has considerable effect on the fluid temperature as shown in Figure 9. Considering the definition of the Prndtle number, one realizes that as P _r increases the fluid thermal conductivity increases which in turn results in increasing the surface heat flux (Table 2) that implies a decrease of the fluid temperature. The thermal radiation parameter affects the fluid temperature as demonstrated in Figure 10. In fact as R _d increases the Rossland radiation absorptivity k ^∗ decreases and hence the radiation heat flux  increases which leads to an increase of rate of the radiative heat transferred to the fluid which in turn elevates the fluid temperature. From Table 2 one can notice that as the parameter value  increases the wall temperature increases also which gives rise to the enhancement of the fluid temperature as elucidated in Figure 11. The effect of the parameter K on the fluid temperature is shown in Figure 12. The value of -θ′(0) decreases with the increase of K as elucidated in Table 2. Such variation enforces the fluid temperature to decrease.

Conclusions

A study of nonlinear radiative flow over a vertical cylinder that moves with nonlinear velocity is given. The problem is formulated using a suitable mathematical model including all parameters influencing the fluid velocity and temperature. The model is then solved numerically and the numerical results in some special case are compared with exact solutions to assure the validity of the numerical method given in this work. The effects of the parameters are investigated and interpreted physically.

Acknowledgements

This work was funded by the University of Jeddah, Jeddah, Saudi Arabia, under grant No. (UJ-22- DR-50). The authors, therefore, acknowledge with thanks the University of Jeddah for its technical and financial support.

References

1. Sakiadis BC (1961) Boundary-layer behavior on continuous solid surfaces: II. The boundary layer on a continuous at surface. AIChE Journal 7: 221-225.
2. Rotte JW, Beek WJ (1969) Some models for the calculation of heat transfer coefficients to a moving continuous cylinder. Chemical Engineering Science 24: 705-716.
3. Ganesan P, Loganathan P (2002) Radiation and mass transfer effects on flow of an incompressible viscous fluid past a moving vertical cylinder. International Journal of Heat and Mass Transfer 45: 4281-4288.
4. Abo-Eldahab EM, Salem AM (2005) MHD Flow and heat transfer of non-Newtonian power-law fluid with diffusion and chemical reaction on a moving cylinder. Heat and Mass Transfer 41: 703-708.
5. Amkadni M, Azzouzi A (2006) On a similarity solution of MHD boundary layer flow over a moving vertical cylinder. Differential Equations and Nonlinear Mechanics 2006: 1-9.
6. Elbashbeshy Elsayed MA, Emam TG, El-Azab MS, et al. (2015) Effect of thermal radiation on flow, heat, and mass transfer of a nanofluid over a stretching horizontal cylinder embedded in a porous medium with suction/injection. Journal of Porous Media 18: 215-229.
7. Rehman A, Iqbal S, Raza SM (2016) Axisymmetric stagnation flow of a micropolar fluid in moving cylinder: An analytical solution. Fluid Mechanics 2: 1-7.
8. Rasheed H, Rehman A, Sheikh N, et al. (2017) MHD boundary layer flow of nanofluid over a continuously moving stretching surface. Applied and Computational Mathematics 6: 265-270.
9. Loganathan1 P, Eswari B (2017) Natural convective flow over moving vertical cylinder with temperature oscillations in the presence of porous medium. Global Journal of Pure and Applied Mathematics 13: 839-855.
10. Manjunatha PT, Gireesha BJ, Prasannakumara BC (2017) Effect of radiation on flow and heat transfer of mhd dusty fluid over a stretching cylinder embedded in a porous medium in presence of heat source. Int J Appl Comput Math 3: 293-310.
11. Bakar SA, Arifin NM, Ali FM, et al. (2018) A stability analysis on mixed convection boundary layer flow along a permeable vertical cylinder in a porous medium filled with a nanofluid and thermal radiation. Appl Sci 8: 1-13.
12. Matteo DL, Alimhillaj P (2019) Novel fluid dynamic nonlinear numerical models of servo-valves for aerospace. International Journal of Mechanics 13: 39-51.
13. Abdel-Wahed MS, El-Said EM (2019) MHD flow and heat transfer over a moving cylinder in a nanofluid under convective boundary conditions and heat generation. Thermal Science 23: 3785-3796.
14. Mkhatshwa MP, Motsa SS, Ayano MS, et al. (2020) MHD mixed convective nanofluid flow about a vertical slender cylinder using overlapping multi-domain spectral collocation approach. Case Studies in Thermal Engineering 18: 1-12.
15. Elbashbeshy Elsayed MA, Emam TG, El-Azab MS, et al. (2016) Slip effects on flow heat and mass transfer of nanofluid over stretching horizontal cylinder in the presence of suction/injection. Thermal Science 20: 1813-1824.
16. Emam TG (2021) Boundary layer flow over a vertical cylinder embedded in a porous medium moving with nonlinear velocity. WSEAS Transactions in Fluid Mechanics 16: 32-36.
17. Emam TG, Elmaboud YA (2017) Three-dimensional magneto-hydrodynamic flow over an exponentially stretching surface. Int J Heat Technology 35: 987-996.