A Hybrid Flower Pollination and Genetic Algorithm for Minimizing the Non-Convex Potential Energy of Molecular Structure

Abstract

Minimizing the molecular potential energy function is a real-life problem which can help to predict the three-dimensional structure of the protein by knowing its steady state of the molecules. In this paper, we propose a new hybrid algorithm by combining the flower pollination algorithm and the genetic algorithm in order to minimize a simplified model of the energy function of the molecule. The proposed algorithm is called Hybrid Flower Pollination and Genetic Algorithm. We use the flower pollination algorithm to balance between the exploration and the exploitation process in the proposed algorithm. Also, we divide the population into sub-populations and applying the arithmetical crossover operator in each sub-population in order to increase the diversity of the search in the algorithm. Further, we apply the genetic mutation operator in the whole population in order to avoid the premature convergence and avoid trapping in local minima. Moreover, we compare the proposed algorithm against 3 benchmark algorithms, in order to investigate its efficiency. The numerical experiment results show that the proposed algorithm is a promising and efficient algorithm and can obtain the global minimum or near global minimum of the molecular energy function of the simplified model with up to 200 degrees of freedom faster than the other comparative algorithms.

Keywords

Flower pollination algorithm, Genetic algorithm, Molecular potential energy function, Global optimization

Introduction

One of the important roles in the determination of ground states or stable states of certain classes of molecular clusters and proteins is to minimize their potential energy functions. In most cases, the potential energy function is nonconvex and therefore has many local minimizers; the minimization of the potential energy function is a very hard problem.

The minimization of the potential energy function problem can be formulated as a global optimization problem. Finding the steady state (ground) of the molecules in the protein can help to predict the 3D structure of the protein, which helps to know the function of the protein. The difficulty of the problem arises from the number of local minimizer of the energy function grows exponentially with the size the molecule [1].

Potential energy functions for proteins typically have multiple local minima whose number increases exponentially with the number of degrees of freedom [2,3]. Many researchers have suggested efficient function-minimization algorithms [4] in order to predict protein structure by exploiting protein-specific properties.

There are several effective methods for determining the native conformation of a protein using energy minimization, for example, the truncated Newton method [5] as well as a combination of the limited memory BFGS quasi-Newton and Hessian-free Newton methods [6], and smoothing methods [7]. However, few of these methods exploit similarities of sequence-related pairs of proteins. The authors in [8] applied Homotopy Optimization using Perturbations and Ensembles (HOPE) to find the global minimizer of the potential energy function associated with a particular protein model. These methods require the differentiability of the objective function. However, computing the Jacobian (derivative of the objective function) is a difficult and expensive operation. Also, the objective function might be no smooth. This is a motivation for many researchers to develop stochastic global optimization algorithms such as Swarm Intelligence (SI) algorithms. SI take inspiration from the behavior of a group of social organisms. These algorithms are applied to solve the energy minimization problem, for example, genetic algorithms [9-12] simulated annealing [3,13-15] random method [1,16-18] variable neighborhood search [19] Particle Swarm Optimization (PSO) (known as a stochastic swarm intelligence algorithm [20]).

This paper studies an approach based on flower pollination, namely Flower Pollination Algorithm (FPA) proposed in 2012 by Xin-She Yang [21] in order to solve the energy minimization problems. Although many researchers are applied the FPA to solve many optimization problems such as [22-27] it suffers from the premature convergence and it may get trapped in local minima especially when it applies to solve large scale global optimization problem such as the problem of minimization of potential energy function. In order to solve the problem of the premature convergence of the FPA, we propose a new hybrid flower pollination algorithm and genetic algorithm in order to solve the molecular potential energy function minimizations. The proposed algorithm is called Hybrid Flower Pollination and Genetic Algorithm (HFPGA). The proposed HFPGA algorithm is based on three mechanisms. The first mechanism is applying the flower pollination algorithm with its powerful performance with the exploration and the exploitation processes. The second mechanism is based on the dimensionality reduction and the population partitioning processes by dividing the population into sub-population and applies the arithmetical crossover operator on each sub-population. The partitioning idea can improve the diversity search of the proposed algorithm. The last mechanism is to avoid the premature convergence by applying the genetic algorithm mutation operator in the whole population. The combination between these three mechanisms accelerates the search and helps the algorithm to reach to the optimal or near optimal solution in reasonable time.

In order to investigate the general performance of the proposed algorithm, we test it on a scalable simplified molecular potential energy function with well-known properties established in [28].

The reminder of the paper is organized as follows. In Section 2, the definition of the molecular potential energy function is described. The overview of the standard flower pollination algorithm and genetic algorithm are presented in Sections 3 and 4, respectively. The proposed algorithm is described in detail in Section 5. The numerical experimental results are presented in Section 6. The conclusion and future works make up Section 7.

Molecular Potential Energy Function

In this section, we present the definition of the molecular potential energy function as follows.

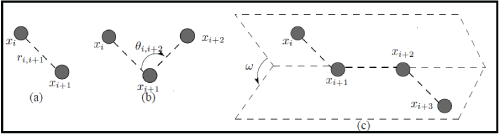
The derivation of the potential energy of a molecule comes from molecular mechanics, which describes molecular interactions based on the principles of Newtonian physics. An empirically derived set of potential energy contributions is used to approximate these molecular interactions. We consider the molecular model that consists of a chain of m atoms centered at x₁, . . . , x_m, in a 3-dimensional space. For every pair of consecutive atoms x_i and x_i+1, let r_i,i+1 be the bond length which is the Euclidean distance between them as in Figure 1a. For every three consecutive atoms x_i, x_i+1, x_i+2, let θ_i,i+2 be the bond angle corresponding to the relative position of the third atom with respect to the line containing the previous two as in Figure 1b. Likewise, for every four consecutive atoms x_i, x_i+1, x_i+2, x_i+3, let ${\omega }_{i,i+3}$ be the angle, called the torsion angle, between the normal through the planes determined by the atoms x_i, x_i+1, x_i+2 and x_i+1, x_i+2, x_i+3 as in Figure 1c.

The force field potentials corresponding to bond lengths, bond angles, and torsion angles are defined in [19] as

$$\begin{array}{l}{E}_1\text{ = }{\displaystyle \sum _{\left(i,j\right)\in M_1}{c}_{ij}^1}{\left(r_{ij}-r_{ij}^0\right)}^2\text{ (1)}\\ E_2\text{ = }{\displaystyle \sum _{\left(i,j\right)\in M_2}{c}_{ij}^2}{\left({\theta }_{ij}-{\theta }_{ij}^0\right)}^2\\ E_3\text{ = }{\displaystyle \sum _{\left(i,j\right)\in M_3}{c}_{ij}^3}\left(1+\cos \left(3{\omega }_{ij}-{\omega }_{ij}^0\right)\right)\end{array}$$

Where $c_{ij}^1$ is the bond stretching force constant, $c_{ij}^2$ is the angle bonding force constant, and $c_{ij}^3$ is the torsion force constant. The constant $r_{ij}^0$ and ${\theta }_{ij}^0$ represent the "preferred" bond length and bond angle, respectively, and the constant ${\omega }_{ij}^0$ is the phase angle that defines the position of the minima. The set of pairs of atoms separated by k covalent bond is denoted by M_k for k = 1, 2, 3.

In addition to the above, there is a potential E₄ which characterizes the 2-body interaction between every pair of atoms separated by more than two covalent bonds along the chain. We use the following function to represent E₄:

$$E_4\text{ = }{\displaystyle \sum _{\left(i,j\right)\in M_3}\left(\frac{{\left(-1\right)}^i}{r_{ij}}\right)}\text{ (2)}$$

Where r_ij is the Euclidean distance between atoms x_i and x_j.

The general problem is the minimization of the total molecular potential energy function, E₁ + E₂ + E₃ + E₄, leading to the optimal spatial positions of the atoms. To reduce the number of parameters involved in the potentials above, we simplify the problem considering a chain of carbon atoms.

In most molecular conformational predictions, all covalent bond lengths and covalent bond angles are assumed to be fixed at their equilibrium values $r_{ij}^0$ and ${\theta }_{ij}^0$, respectively. Thus, the molecular potential energy function reduces to E3 + E4 and the first three atoms in the chain can be fixed. The first atom, x₁, is fixed at the origin, (0, 0, 0); the second atom, x₂, is positioned at (-r₁₂, 0, 0); and the third atom, x₃, is fixed at (r₂₃ cos(θ₁₃ ) - r₁₂ , r₂₃ sin(θ₁₃ ), 0).

Using the parameters previously defined and Eq. (1) and Eq. (2), we obtain

$$E\text{ = }{\displaystyle \sum _{\left(i,j\right)\in M_3}\left(1+\cos \left(3{\omega }_{ij}\right)\right)}+{\displaystyle \sum _{\left(i,j\right)\in M_3}\left(\frac{{\left(-1\right)}^i}{r_{ij}}\right)}\text{ (3)}$$

Although the molecular potential energy function (3) does not actually model the real system, it allows one to understand the qualitative origin of the large number of local minimizers the main computational difficulty of the problem, and is likely to be realistic in this respect.

Note that E₃, Eq. (1), is expressed as a function of torsion angles, and E₄, Eq. (2), is expressed as a function of Euclidean distance. To represent Eq. (3)

as a function angles only, we can use the result established in [29] and obtain

$$\begin{array}{l}{r}_{il}^2\text{ = }{r}_{ij}^2+r_{jl}^2-r_{ij}\left(\frac{r_{jl}^2+r_{jk}^2-r_{kl}^2}{r_{jk}}\right)\cos \left({\theta }_{ik}\right)\\ -r_{ij}\left(\frac{\sqrt{4r_{jl}^2{r}_{jk}^2-{\left(r_{jl}^2+r_{jk}^2-r_{kl}^2\right)}^2}}{r_{jk}}\right)\sin \left({\theta }_{ik}\right)\cos \left({\omega }_{il}\right)\text{(4)}\end{array}$$

for every four consecutive atoms x_i, x_j, x_k, x_l. Using the parameters previously defined, we have

$$r_{ij}\text{ = }\sqrt{10.60099896-4.141720682\left(\cos \left({\omega }_{il}\right)\right)}\text{ (5)}$$ for all $\left(i,j\right)\in M_3$

From Eq. (3) and Eq. (5), the expression for the potential energy as a function of the torsion angles takes the form

$$E\text{ = }{\displaystyle \sum _{\left(i,j\right)\in M_3}\left(1+\cos \left(3{\omega }_{ij}\right)+\frac{{\left(-1\right)}^i}{\sqrt{10.60099896-4.141720682\left(\cos \left({\omega }_{ij}\right)\right)}}\right)}\text{ (6)}$$

Where i = 1, . . . , m-3 and m is the number of atoms in the given system. as shown in Figure 1 (c).

The problem is then to find ${\omega }_{14},{\omega }_{25},\mathrm{...},{\omega }_{\left(m-3\right)m}$, where ${\omega }_{ij}\in \left[0,5\right]$, which corresponds to the global minimum of the function E, represented by Eq. (6). E is a non-convex function involving numerous local minimizers even for small molecules.

Finally, the function f (x) can be defined as

$$f\left(x\right)\text{ = }{\displaystyle \sum _{i=1}^n\left(1+\cos \left(3x_i\right)+\frac{{\left(-1\right)}^i}{\sqrt{10.60099896-4.141720682\left(\cos \left(x_i\right)\right)}}\right)}\text{ (7)}$$

and 0 ≤ x_i ≤ 5, i = 1, . . . , n.

Despite this simplification, the problem remains very difficult. A molecule with as few as 30 atoms has 2²⁷ = 134,217,728 local minimizers.

Standard Flower Pollination Algorithm

In the following, we will give an overview of the main concepts and structure of the flower pollination algorithm.

Main concepts

The Flower Pollination Algorithm (FPA) is a nature-inspired population based algorithm developed by Yang in 2012 [21]. The main objective of the flower pollination is to produce the optimal reproduction of plants by surviving the most fittest flowers in the flowering plants. The flower pollination process is an optimization process of plants in species.

Characteristics of flower pollination

The pollination process is very important for flower reproduction. The process is done by transferring the pollen by using pollinators such as insects, birds, bats,...etc. There are two major processes for transferring the pollen.

Biotic and cross pollination process

In the biotic pollination, pollen is transferred from one flower to another flower in different plant by a pollinator such as insects and birds. Biotic, cross-pollination may occur at long distance and is considered as a global pollination process with pollinators performing Lévy flights.

Abiotic and self pollination process

Abiotic or self pollination process is a fertilization of one flower from pollen of the same flower of different flower of the same plant. In this type of pollination, wind and diffusion in water help pollination of such flowering plants. Abiotic and self pollination process are considered as local pollination.

Flower pollination algorithm

We highlight the main steps of the standard Flower Pollination Algorithm (FPA) as follows. (Algorithm 1)

Step 1

The algorithm starts by setting the initial values of the most important parameters such as the population size pop, switch probability p and the maximum number of generations MGN (Line 1).

Step 2

The initial population x_i, i = {1, . . . , n} is randomly generated and the fitness function of each solution f (x_i ) in the population is evaluated by calculating its corresponding objective function (Lines 2-5).

Step 3

The following steps are repeated until the termination criterion is satisfied, which is to reach the desired number of generations MGN.

Step 3.1

The global pollination process is started by generating a random number r for each solution x_i, where r ∈ [0, 1].

Step 3.2

If r < p, the new solution is generated by a Lévy distribution as follows.

$${\text{X}}_i^{t+1}\text{ = }{\text{X}}_i^{t+1}+L\left({\text{X}}_i^t-g^{\ast }\right)\text{ (8)}$$

Where g^∗ is the current best solution, L is a Lévy flight, L > 0 and calculated by the following equation.

$$L\sim \frac{\lambda \Gamma \left(\lambda \right)sin\left(\pi \lambda /2\right)}{\pi }\frac{1}{s^{1+\lambda }},s\gg s_0>0\text{ (9)}$$

Γ (λ) is the standard gamma function and this distribution is valid for large steps s > 0 (Lines 8-12).

Step 3.3

Otherwise, the local pollination process is started by generating a random number, ε, ε ∈ [0, 1] and the new solution is generated as the following

$${\text{X}}_i^{t+1}\text{ = }{\text{X}}_i^t+\in \left({\text{X}}_j^t-{\text{X}}_k^t\right)\text{ (10)}$$

Where $X_i^t,X_j^t$ are pollens (solutions) from the different flowers of the same plant species. If $X_i^t$ comes from the same species or selected from the same population, we have a local random walk (Lines 13-17).

Step 3.4

Evaluate each solution $X_i^{t+1}$ in the population and update the solutions in the population according to their objective values (Lines 19-26).

Step 3.5

Rank the solutions and find the current best solution g^∗.

Step 4

Produce the best found solution so far.

Genetic Algorithm

Genetic algorithms (GAs) have been developed by J. Holland to understand the adaptive processes of natural systems [30]. Then, they have been applied to optimization and machine learning in the 1980s [31,32]. Traditionally, GAs is associated with the use of a binary representation but nowadays one can find GAs that use other types of representations (continues). GA usually applies a crossover operator by mating the parents (individuals) and a mutation operator that randomly modifies the individual contents to promote diversity to generate a new offspring. GAs uses a probabilistic selection that is originally the proportional selection. The replacement (survival selection) is generational, that is, the parents are replaced systematically by the offspring's. The crossover operator is based on the n-point or uniform crossover while the mutation is a bit flipping.

Selection operator

The selection stage is important in GA in order to chose the individuals from the population for crossover operator. There are many kinds of selection operator such as roulette wheel selection, rank selection, tournament selection and elitist selections.

Mutation operator

The main role of the mutation in GA is to increase the exploration process of the algorithm and avoid the premature convergence in the population by associating a random number from (0,1) with each gene in each individual in the population P and mutate the gene which their associated number less than Pm.

Arithmetical crossover operator

An arithmetical crossover operator [33] is applied on each partition (sub-population) in the proposed HFPGA algorithm in order to explore the search space and increase the diversity of the search. Procedure 1 shows the main steps of the arithmetical crossover operator.

Procedure 1 Crossover (p¹,p² )

1. Randomly choose $\lambda \in \left(0,1\right)$.

2. Two offspring $c^1\text{ = }\left(c_1^1,\mathrm{...},c_D^1\right)$ and $c^2\text{ = }\left(c_1^2,\mathrm{...},c_D^2\right)$ are generated

from parents $p^1\text{ = }\left(p_1^1,\mathrm{...},p_D^1\right)$ and $p^2\text{ = }\left(p_1^2,\mathrm{...},p_D^2\right)$, where

$c_i^1\text{ = }\lambda p_i^1+\left(1-\lambda \right)p_i^2\text{ ,}$

$c_i^2\text{ = }\lambda p_i^2+\left(1-\lambda \right)p_i^1\text{ ,}$

$i\text{ = 1,}\mathrm{...}\text{,}D\text{.}$

3. Return.

The Proposed HFPGA Algorithm

The main structure of the proposed HFPGA algorithm is presented in Algorithm 2 and the main steps of the proposed algorithm are presented as follows (Algorithm 2).

Step 1

The proposed HFPGA algorithm starts by setting its parameter values such as the switch probability p, the variables number at each partition ν, the number of solution at each population size η, partitions number Partno, probability of genetic crossover P_c, probability of genetic mutation P_m and maximum number of iterations max_itr (Line 1).

Step 2

The iteration counter t is initialized and the initial population is randomly generated (Lines 2-3).

Step 3

For each solution $X_i^t$ in the population, a new solution $X_i^{t+1}$ is generated by applying one of the two flower pollination operators (global pollination) or (local pollination) depending on the value of the generated random number r and the switching probability p (Lines 7-15).

Step 4

Evaluate the fitness function of all solutions in the population and select an intermediate population from the current one (Lines 16-17).

Step 5

In order to increase the diversity of the search and overcome the dimensionally problem, the current population is partitioned into into ν × η, where ν is the number of variables at each partition while η is the number of solutions at each population (Lines 18-21).

Step 6

The genetic mutation operator is applied in the whole population in order to avoid the premature convergence (Line 22).

Step 7

The solutions in the population are evaluated by calculating its fitness function, the iteration counter t is increased and the overall processes are repeated until termination criteria are satisfied. (Lines 23-25).

Step 8

Finally, the best found solution is presented (Line 26).

Numerical Experiments

We test the proposed HFPGA on a simplified model of molecular potential energy function with various sizes and compare the results of the proposed algorithm against 3 benchmark algorithms. We program HFPGA via MATLAB and take the results of the compared algorithms from their original papers. In the following subsection, we report the parameter setting of the proposed algorithm with more details. Also we present the performance analysis of the proposed algorithm by comparing its results against the results of other algorithms.

Parameter setting

We summarize the parameters of the HFPGA algorithm with their assigned values in Table 1. These values are based on our preliminary numerical experiments or the common setting in the literature.

- Population Size pop. The experimental tests show that the best population size is pop = 25, increasing this number will increase the evaluation function values without any improvement in the obtained results.

- Switch Probability p. The switch probability parameter p is responsible of switching between the exploration and exploitation process in the flower pollination algorithm. In our experiment, we find that the best value of the p parameter is to set to 0.4. Increasing or decreasing this value can negatively effect on the results.

- Probability of Crossover P_c. We apply arithmetical crossover operator for each partition in the population and we reach that the best value of the probability of crossover is to set to 0.6.

- Probability of Mutation P_m. In order to avoid the premature convergence, we apply a mutation on the whole population with value 0.01.

- Partitioning Variables ν and η. It turns out that the best sub-population size is to be ν × η, where ν and η equal to 5.

Comparison between the standard flower pollination algorithm and the proposed HFPGA for minimizing molecular potential energy function

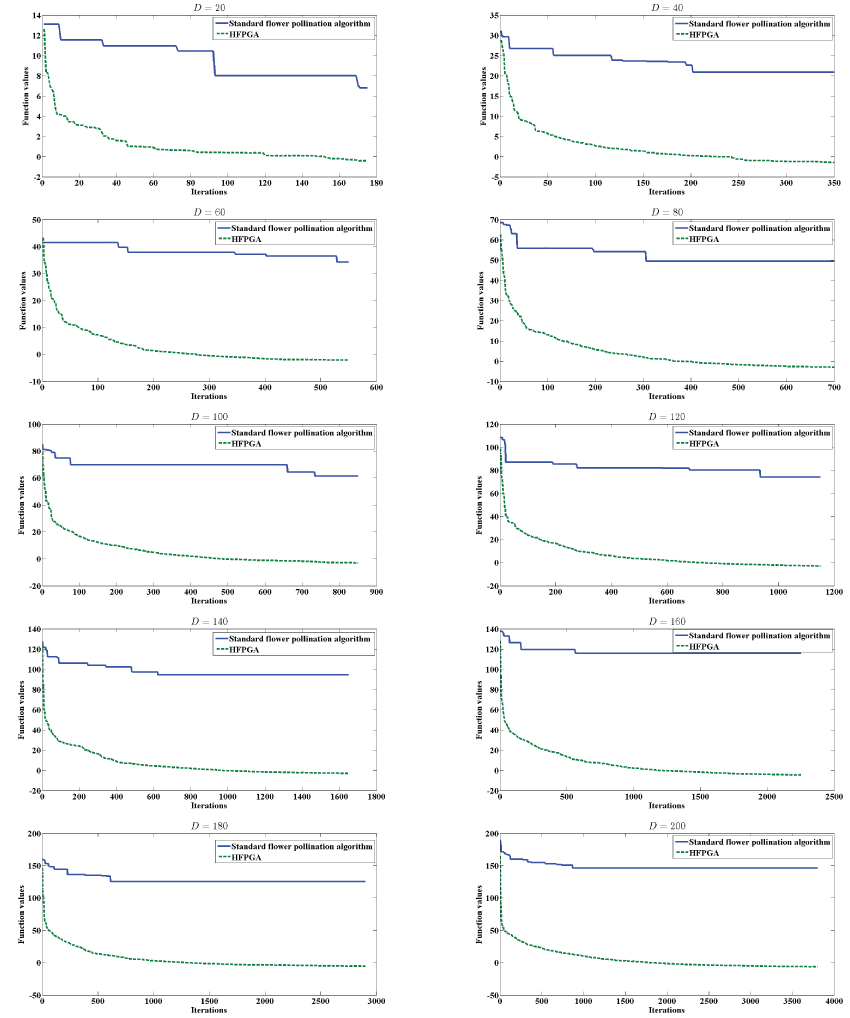
In order to test the efficiency of the proposed algorithm, we compare the general performance of the standard flower pollination algorithm against the proposed HFPGA as shown in Figure 2. The main termination criterion reaches to 99% of the global minimum. We set the same parameter values for both algorithms in order to make a fair comparison. We plot the results in Figure 2 by plotting the values of function values versus the number of iterations for a simplified model of the molecule with different size from 20 to 200 dimensions. In Figure 2, the solid line represents the standard flower pollination algorithm results, while the dotted line represents the proposed HFPGA. Figure 2 shows that the function values rapidly decrease as the number of iterations increases for HFPGA results than those of the standard flower pollination algorithm. We can conclude from Figure 2 that the combination between the standard flower pollination algorithm and genetic algorithm with the population partitioning mechanism can improve the performance and accelerate the convergence of the proposed algorithm.

HFPGA and other algorithms

We compare the HFPGA against three benchmark algorithms Variable Neighborhood Search (VNS), (VNS-123), (VNS-3) methods [19] and GeneticAlgorithm (GA) [9]. In order to make fair comparison, we apply the same termination criterion of the other compared algorithms which stops the search when the algorithm reaches to 99% of the global minimum function value.

Comparison results between VNS-123, VNS-3, GA and HFPGA

our HFPGA and other 3 benchmark algorithms. We report the results in Table 2 and take the results of the other compared algorithms from their original papers [9]. In Table 2, we report the Average (Avg) and the standard Deviation (Dev) of the evaluation function values over 30 runs. For D > 100, the results of GA were not reported in its original paper, so we put the mark (-) in GA results. We report the best results between the compared algorithms in boldface text. The results in Table 2 show that the proposed HFPGA succeeds and obtains the desired objective value of each molecular size faster than the other algorithms in all cases.

Wilcoxon signed-ranks test

Wilcoxons test is a nonparametric procedure or distribution free test that used in a hypothesis testing situation involving a design with two samples [34-36]. As for the sign test, the Wilcoxon signed rank sum test is used to test the null hypothesis that the median of a distribution is equal to some value. It can be used either in place of a one-sample t-test or in place of a paired t-test or for ordered categorical data where a numerical scale is inappropriate but where it is possible to rank the observations. It is a pairwise test that aims to detect significant differences between the behaviors of two algorithms. ρ is the probability of the null hypothesis being true. The result of the test when ρ < 0.05 which indicates a rejection of the null hypothesis, while ρ > 0.05 indicates a failure to reject the null hypothesis. The R⁺ is the sum of positive ranks, while R^- is the sum of negative ranks.

We use Wilcoxon signed-ranks test to compare the results of HFPGA against the results of VNS-123, VNS-3 and GA and record the comparison in Table 3. We can conclude from Table 3 that the proposed HFPGA is a significant algorithm and it is better than the other compared algorithms.

Conclusion and Future Works

In this paper, we propose a new hybrid flower pollination algorithm and genetic algorithm in order to minimize the potential energy function of a simplified model of the molecular. The problem of finding the global minimum of the molecular energy function is difficult to solve since the number of the local minima increases exponentially with the molecular size. We call the proposed algorithm by Hybrid Flower Pollination and Genetic Algorithm (HFPGA). In the HFPGA, we apply three mechanisms. The first mechanism is based on the balancing between the exploration and the exploitation processes in the flower pollination algorithm. The second mechanism is based on the dimensionality reduction and the population partitioning processes in order to increase the diversity of the search in the proposed algorithm. The third mechanism is based on escaping from trapping in local minima by applying the genetic mutation process on the whole population in order to avoid the premature convergence of the solutions. The experimental results show that the proposed algorithm is a promising algorithm and can obtain the optimal or near optimal global minimum of the molecular energy function faster than the other comparative algorithms. In the future work, we would like to do the following:

- Modify the proposed algorithm in order to be able to solve large scale unconstrained global optimization problems with dimensions D > 1000.

- Use the proposed algorithm and its enhancement to deal with large scale problem in constrained optimization, engineering problems [37], integer programming and minimax problems [38-41] by employing various constraint handling strategies [42,43].

- Utilize Enhanced Leader PSO (ELPSO) [44] and its modifications/hybridization to extend the results in [37,45-47].

Acknowledgements

The authors are grateful to the anonymous referees for their valuable comments and helpful suggestions which greatly enhanced the paper's quality. The research of the 1^st author is supported in part by the Natural Sciences and Engineering Research Council of Canada (NSERC). The postdoctoral fellowship of the 2^nd author is supported by NSERC.

References

1. Wales DJ, Scheraga HA (1999) Global optimization of clusters, crystals and biomolecules. Science 285: 1368-1372.
2. Li Z, Scheraga HA (1987) Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proc Natl Acad Sci U S A 84: 6611-6615.
3. Wilson SR, Cui W, Moskowitz JW, et al. (1988) Conformational analysis of flexible molecules: Location of the global minimum energy conformation by the simulated annealing method. Tetrahedron Letters 29: 4373-4376.
4. Ngo JT, Marks J (1992) Computational complexity of a problem in molecular structure prediction. Protein Eng 5: 313-321.
5. Xie D, Schlick T (1999) Efficient implementation of the truncated-Newton algorithm for large-scale chemistry applications. SIAM J Optim 10: 132-154.
6. Das B, Meirovitch H, Navon IM (2003) Performance of enriched methods for large unconstrained optimization as applied to models of proteins. J Comput Chem 24: 1222-1231.
7. Schelstraete S, Schepens W, Verschelde H (1998) Energy minimization by smoothing techniques: A survey. In: Balbuena PB, Seminario JM, Molecular Dynamics. From Classical to Quantum Methods. Elsevier, New York, 129-185.
8. Dunlavy DM, O'Leary DP, Klimov D, et al. (2005) HOPE: A homotopy method for unconstrained minimization. Journal of Computational Biology 12: 1275-1288.
9. Barbosa HJC, Lavor C, Raupp FM (2005) A GA-simplex hybrid algorithm for global minimization of molecular potential energy function. Ann Oper Res 138: 189-202.
10. Brodmeier T, Pretsch E (1994) Application of genetic algorithms in molecular modeling. J Comput Chem 15: 588-595.
11. Hedar A, Ali AF, Hassan T (2011) Genetic algorithm and Tabu search based methods for molecular 3D-structure prediction. Numerical Algebra, Control and Optimization (NACO) 1: 191-209.
12. Le Grand SM, Merz Jr KM (1993) The application of the genetic algorithm to the minimization of potential energy functions. J Global Optim 3: 49-66.
13. Shin JK, Jhon MS (1991) High directional Monte Carlo procedure coupled with the temperature heating and annealing as a method to obtain the global energy minimum structure of polypeptides and proteins. Biopolymers 31: 177-185.
14. Wilson SR, Cui W (1990) Applications of simulated annealing to peptides. Biopolymers 29: 225-235.
15. Zhao J, Tang HW (2006) An improved simulated annealing algorithm and its application. Journal of Dalian University of Technology 46: 775-780.
16. Floudas CA, Klepeis JL, Pardalos PM (1999) Global optimization approaches in protein folding and peptide docking. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, American Mathematical Society.
17. Pardalos PM, Shalloway D, Xue GL (1994) Optimization methods for computing global minima of nonconvex potential energy function. J Glob Optim 4: 117-133.
18. Troyer JM, Cohen FE (1991) Simplified models for understanding and predicting protein structure. Reviews in Computational Chemistry (Wiley-VCH) 2: 57-80.
19. Draz˘ic´ M, Lavor C, Maculan N, et al. (2008) A continuous variable neighbor- hood search heuristic for finding the three-dimensional structure of a molecule. European Journal of Operational Research 185: 1265-1273.
20. Bansal JC, Deep SK, Katiyar VK (2010) Minimization of molecular potential energy function using particle swarm optimization. International Journal of Applied Mathematics and Mechanics 6: 1-9.
21. Yang XS (2012) Flower pollination algorithm for global optimization. In: Durand-Lose J, Jonoska N, Unconventional computation and natural computation. Springer, Berlin, Heidelberg.
22. Chiroma H, Shuib NLM, Muaz SA, et al. (2015) A review of the applications of bio-inspired flower pollination algorithm. Procedia Computer Science 62: 435-441.
23. Chiroma H, Khan A, Abubakar AI, et al. (2016) A new approach for forecasting OPEC petroleum consumption based on neural network train by using flower pollination algorithm. Applied Soft Computing 48: 50-58.
24. Galvez J, Cuevas E, Avalos O (2017) Flower pollination algorithm for multimodal optimization. International Journal of Computational Intelligence Systems 10: 627-646.
25. Prathiba R, Moses MB, Sakthivel S (2014) Flower pollination algorithm applied for different economic load dispatch problems. International Journal of Engineering and Technology (IJET) 6: 1009-1016.
26. Salgotra R, Singh U (2017) Application of mutation operators to flower pollination algorithm. Expert Systems with Applications 79: 112-129.
27. Valenzuela L, Valdez F, Melin P (2017) Flower pollination algorithm with fuzzy approach for solving optimization problems. In: Melin P, Castillo O, Kacprzyk J, Nature-Inspired Design of Hybrid Intelligent Systems. Springer, 357-369.
28. Lavor C, Maculan N (2004) A function to test methods applied to global minimization of potential energy of molecules. Numerical Algorithms 35: 287-300.
29. Pogorelov A (1987) Geometry. Mir Publishers, Moscow.
30. Holland JH (1975) Adaptation in natural and artificial systems. University of Michigan Press, Cambridge, MA, USA.
31. De Jong KA (1985) Genetic algorithms: A 10-year perspective. International Conference on Genetic Algorithms, 169-177.
32. Goldberg DE (1989) Genetic algorithms in search, Optimization, and machine learning. Addison-Wesley Longman Publishing Co., Inc. Boston, MA, USA.
33. Michalewicz Z (1996) Genetic algorithms + data structures = evolution programs. Springer, Berlin.
34. Garcia S, Fernandez A, Luengo J, et al. (2009) A study of statistical techniques and performance measures for genetics-based machine learning, accuracy and interpretability. Soft Comput 13: 959-977.
35. Sheskin DJ (2003) Handbook of parametric and nonparametric statistical procedures. CRC Press, Boca Raton.
36. Zar JH (1999) Biostatistical analysis. Prentice Hall, Englewood Cliffs.
37. Ali AF, Tawhid MA (2016) A Hybrid PSO and DE algorithm for solving engineering optimization problems. Appl Math Inf Sci 10: 431-449.
38. Ali AF, Tawhid MA (2016) Hybrid simulated annealing and pattern search method for solving minimax and integer programming problems. Pacific Journal of Optimization 12: 151-184.
39. Ali AF, Tawhid MA (2016) A hybrid cuckoo search algorithm with Nelder Mead method for solving global optimization problems. Springerplus 5: 473.
40. Tawhid MA, Ali AF (2017) A Hybrid grey wolf optimizer and genetic algorithm for minimizing potential energy function. Memetic Comp 1-13.
41. Tawhid MA, Ali AFA (2016) Simplex social spider algorithm for solving integer programming and minimax problems. Memetic Comp 8: 169-188.
42. Wang Y, Wang BC, Li HX, et al. (2016) Incorporating objective function information into the feasibility rule for constrained evolutionary optimization. IEEE Trans Cybern 46: 2938-2952.
43. Jordehi AR (2015) A review on constraint handling strategies in particle swarm optimization. Neural Comput & Applic 26: 1265-1275.
44. Jordehi AR (2015) Enhanced leader PSO (ELPSO): A new PSO variant for solving global optimization problems. Applied Soft Computing 26: 401-417.
45. Ali AF, Tawhid MA (2015) Hybrid particle swarm optimization with a modified arithmetical crossover for solving unconstrained optimization problems. INFOR: Information Systems and Operational Research 53: 125-141.
46. Ali AF, Tawhid MA (2017) Hybrid particle swarm optimization and genetic algorithm for minimizing potential energy function. Ain Shams Engineering Journal 8: 191-206.
47. Tawhid MA, Ali AF (2016) Simplex particle swarm optimization with arithmetical crossover for solving global optimization problems. OPSEARCH 53: 705-740.