On the Comparison of Ten Pitch Trim Strategies for Cruise Drag Minimization

Abstract

The methods of minimization or maximization of lift, drag and pitching moment are extended to multiple coupled control surfaces with polynomial dependence of any degree on the control surface deflections. This serves as an introduction to the problem of minimization of cruise drag with pitch trim and unchanged lift, i.e. same airspeed and altitude, that is considered for a flying-wing configuration, using ten distinct strategies. Among the first four non-optimal strategies, only strategy II of using the centerbody elevator alone leads to drag reduction, albeit with a large deflection and increased angle-of-attack. There is drag increase for the strategies: (I) of equal deflection of all control surfaces; (III) preferential deflection of inner control surfaces with an aeroelastic limit of 7.5º; (VI) equal contribution to lift for all control surfaces. The two optimal strategies using Lagrange multipliers after a few interactions give: (strategy IV) a drag reduction for a good initial condition like strategy II; (strategy V) a drag increase for a poor initial condition like strategy I. A sub-optimal strategy VII of using multiples of optimal deflections, with a multiplication factor determined by lift equilibrium, does not change the angle-of-attack, and thereby increases drag; a drag decrease can be obtained (strategy VIII) freeing the constraint on angle-of-attack. The strategy IX of deflecting all control surfaces in two groups to minimize trim drag, leads to a larger angle-of-attack, and thereby increases drag. The strategy X of using the two most effective control surfaces with opposite drag slopes gives the best compromise: (i) Lift balance with unchanged angle-of-attack; (ii) Second best drag reduction with small control surfaces deflections. The small control surfaces deflections justify the use of linear aerodynamics and reduce the risk of adverse aeroelastic effects.

Keywords

Multiple control surfaces, Flying-wing configuration, Optimization, Cruise drag, Pitch trim

Nomenclature

$\overline{c}$ : Mean Aerodynamic Chord

$C_{D_i}$ : Dimensionless drag coefficient of the control surface i

${C^{\prime }}_{D_i}$ : Derivative of the drag coefficient of the control surface i

${C^{\prime }}_{D_i}$ : Derivative of the drag coefficient with regard to the deflection of the control surface i

${C^{\prime }}_{M_i}$ : Derivative of the drag coefficient

$C_{M_i}$ : Pitch control coefficient of the control surface i

${C^{\prime }}_{M_i}$ : Derivative pitch control coefficient with regard to the deflection of the control surface

D : Trim drag

$L_i$ : Moment arm of the control surface i

$l_i$ : Given c.g. position of the control surface i

M : Pitching moment

q : Dynamic pressure

V : Airspeed

$S_i$ : Area of the control surface i

$S_0$ : Total control surface area

S: Wing area

α: Angle of attack

α₀: Cruise angle of attack

${\delta }_i$ : Deflection of the control surface i

${\overline{\delta }}_i$ : Optimal deflection of the control surface i

$\lambda$ : Lagrange multiplier

$\rho$ : Mass density of atmospheric air

Abbreviations

AOA: Angle of Attack

BWB: Blended Wing Body

c.g.: Center of Gravity

FW: Flying-Wing

Ma: Mach Number

Introduction

The minimization of cruise drag is an instance of the general problem of maximization or minimization control forces and moments (6), that is simpler assuming: (i) Decoupled control surfaces such that the deflection of one does not affect the others; (ii) Forces and moments specified by quadratic functions of the deflections of control surfaces that are sufficient to specify base values for equilibrium, first-order derivatives for stability and second-order derivatives for optimization. The maximization or minimization of control forces and moments can be extended to (i) Interacting control surfaces, such that the deflection of one affects the others (6.1); (ii) Forces and moments specified by polynomials of any degree of the deflection angles of control surfaces, for higher accuracy. The (i) Coupled and (ii) High-order controls (6.3) Increase the data needed to fully address (6.4) The performance, stability and optimization problems.

The main aim of the paper in (7-10) to compare ten pitch trim strategies for cruise drag minimization that is most relevant to reduce fuel consumption, emissions, and operational costs [1-13]. The case of a blended-wing body (BWB) configuration [14-26] is used to compare eight pitch trim strategies for cruise drag minimization: (i) The four simplest non-optimal pitch trim strategies, which give a first feeling for the flight physics of the problem (7); (ii) The preceding can serve as initial condition for the two optimal pitch trim strategies, which are recursive and inevitably more complex (8); (iii) The preceding suggest four further pitch trim strategies which, although sub-optimal, may prove quite effective and relatively simple (9-10).

The comparison of the ten pitch trim strategies (11) was initially motivated by (i) Reduction of cruise drag, but raises other relevant and related issues, e.g.: (ii) If unchanged lift is required, to keep the same airspeed and altitude as for the untrimmed flight condition, can this be achieved with the same untrimmed angle-of-attack (AOA) or is a higher value needed?; (iii) The largest control surface deflections required are sufficiently small to avoid concerns about adverse aeroelastic [27-31] or aerodynamic [32-57] effects, e.g. loss of control effectiveness [58-65] or control inversion, and shock wave formation and boundary layer separation?; (iv) The AOA of the aircraft and deflections of all control surfaces are within the range where linear or weakly non-linear methods can be applied with confidence? It should be borne in mind that there are many approaches to drag reduction [66,67], and the optimization of control surface deflections is just one of them. The comparison of the ten pitch trim strategies according to these criteria shows that the most complex or demanding is not necessary the best; it is possible to find a relatively simple strategy X, which achieves pitch trim drag reduction relative to the untrimmed flight condition, while also keeping the low untrimmed AOA and using moderate deflections of only the two most effective control surfaces (10).

Minimization or Maximization of Control Forces and Moments

Considering an aircraft with multiple control surfaces, the choice of deflections which maximize and minimize any force or moment is considered without making the assumptions that: (a) The controls are independent or decoupled; (b) The control forces and moments are specified by quadratic functions of the deflections. Using these assumptions (a,b) leads [68] to the simplest application of the method to find the extrema (maxima and minima) of the control forces and moments, whether they lie inside the interval of possible deflections or at the limit deflections. The methods presented next extend earlier results [68] and apply (6) to the case of coupled or interdependent controls (6.1) and to the case of control forces and moments specified by a polynomial or arbitrary degree of the deflections (6.2), thus removing one at a time of the two restrictions (a) and (b) above; both restrictions can be removed simultaneously in the general case of coupled controls specified by high-order polynomials (6.3), which requires more aerodynamic data (6.4). The forces and moments along the three axis are denoted (1b) by $C_{\alpha }$ with the index $\alpha$ running (1a) from one to six:

$\alpha =1,2,\mathrm{...},6:C_{\alpha }=\left\{X,Y,Z,L,M,N\right\}\text{ (1a,b)}$

the index i numbers the N control surfaces:

$i=1,\mathrm{...},N=5:i=\left\{\text{body flap,inner flap,middle flap,outer flap,rudder}\right\}\text{ (2a,b)}$

Effect of mutual interaction between controls

In the case of interdependent or coupled controls, the force and moment on one surface are affected at most by the deflections of all others:

$C_{\alpha i}=C_{\alpha i0}+{\displaystyle \sum _{i=1}^N{a}_{\alpha ij}{\delta }_j}+{\displaystyle \sum _{j,k=1}^N{b}_{\alpha ijk}{\delta }_j{\delta }_k}\text{ (3)}$

Assuming still a polynomial of second degree: (i) The static values are unchanged; (ii) The slopes are specified by a matrix (4a) indicating the effect of the deflection of control surface ${\delta }_j$ on the forces and moments on control surface $C_{\alpha i}$:

$$a_{\alpha ij}=\frac{\partial C_{\alpha i}}{\partial {\delta }_j};2b_{\alpha ijk}=\frac{{\partial }^2{C}_{\alpha i}}{\partial {\delta }_j\partial {\delta }_k}\text{ (4a,b)}$$

(iii) The curvatures (4b) involve a multiplicity with three indices.

The extremum cannot be found separately for each surface, but only for all together:

$0=d{C}_{\alpha }={\displaystyle \sum _{i=1}^{N}d{C}_{\alpha i}}={\displaystyle \sum _{i,j=1}^{N}d{\delta }_j\left(a_{\alpha ij}+2{\displaystyle \sum _{k=1}^N{b}_{\alpha ijk}{\overline{\delta }}_k}\right)}\text{ (5)}$

where the multiplicity of slopes (4b) is symmetric in the last two indices (6a)

$$b_{\alpha ijk}=b_{\alpha ikj}\iff \frac{{\partial }^2{C}_{\alpha i}}{\partial {\delta }_j\partial {\delta }_k}=\frac{{\partial }^2{C}_{\alpha i}}{\partial {\delta }_k\partial {\delta }_j}\text{ (6a,b)}$$

on account of (6b). The deflections for the extrema are given by (7)

${\overline{\delta }}_{i,\alpha }=-\frac{1}{2}{\displaystyle \sum _{j,k=1}^N{a}_{\alpha ij}{\left(b_{\alpha ijk}\right)}^{-1}}\text{ (7)}$

where ${\left(b_{\alpha ijk}\right)}^{-1}$ is the inverse matrix of $b_{\alpha ijk}$ with regard to $jk$. The extremum will be a maximum/minimum if the second-order differential is positive/negative:

$$\begin{array}{l}{d}^2{C}_{\alpha }={\displaystyle \sum }_{i=1}^N{d}^2{C}_{\alpha i}={\displaystyle \sum }_{i,j,k=1}^N\left(\frac{{\partial }^2{C}_{\alpha i}}{\partial {\delta }_i\partial {\delta }_j}\right)d{\delta }_{i}d{\delta }_j\text{ (8a,b)}\\ =2{\displaystyle \sum }_{i,j,k=1}^N{b}_{\alpha ijk}d{\delta }_{j}d{\delta }_k\left\{\begin{array}{cc}>0& \text{minimum,}\\ <0& \text{maximum;}\end{array}\right.\end{array}$$

this is equivalent to the matrix $b_{\alpha ijk}$ being positive/negative definite in $\left(j,k\right)$ for every $i$, i.e. having all eigenvalues real and positive (negative):

$$b_{\alpha ijk}=\left\{\begin{array}{c}\text{is positive-definite implies }{\overline{\delta }}_i\text{ is local minimum, }\\ \text{is negative-definite implies }{\overline{\delta }}_i\text{ is local maximum}\text{. }\end{array}\right.\text{ (9a,b)}$$

If these conditions [(9a) or (9b)] are not all met for some $\left(i,\alpha \right)$ or the values (7) lie outside the range of possible deflections, the maximum/minimum occur at the extreme deflections. The case of coupled controls (3) reduces to independent controls when for each $\alpha$ the matrix $a_{\alpha ij}$ and multiplicity $b_{\alpha ijk}$ are replaced by two vectors $\left(a_{\alpha i},b_{\alpha i}\right)$.

Controls specified by polynomials of high-degree

Next the assumption of decoupled controls is retained, but the control forces and moments are allowed to be polynomials of any degree M:

$$C_{\alpha i}={\displaystyle \sum _{m=1}^M{A}_{\alpha i}^{(m)}{\left({\delta }_i\right)}^m}\text{ (10)}$$

where: (i) The static values (11a), slopes (11b) and curvatures (11c) are retained:

$$\begin{array}{l}{A}_{\alpha i}^{(0)}\equiv C_{\alpha i}\left(0\right)\equiv C_{\alpha 0},A_{\alpha i}^{(1)}=\frac{d{C}_{\alpha i}}{d{\delta }_i}\equiv a_{\alpha i},\text{ (11a-d)}\\ 2A_{\alpha i}^{(2)}=\frac{d^2{C}_{\alpha i}}{d{\delta }_i{}^2}\equiv 2b_{\alpha i},m!A_{\alpha i}^{(m)}\equiv \frac{d^m{C}_{\alpha i}}{d{\delta }_i{}^m},\end{array}$$

and derivatives of order m up to M are added. The extremum can be obtained independently for each decoupled surface. The total extremum is the sum of partial extrema. Thus only partial extrema need to be considered. The extremum corresponds to the vanishing of the derivative of a polynomial:

$$0=\frac{d{C}_{\alpha i}}{d{\delta }_i}={\displaystyle \sum _{m=1}^M{A}_{\alpha i}^{(m)}m{\left({\overline{\delta }}_i\right)}^{m-1}}\text{ (12)}$$

In the case of second-degree there would be only one root, whereas in the case of degree M there are M-1 roots. Of these roots, those with positive/negative second-order derivative can be local minima/maxima:

$$\begin{array}{l}\frac{d^2{C}_{\alpha i}}{d{\overline{\delta }}_i{}^2}={\displaystyle \sum _{m=2}^M{A}_{\alpha i}^{(m)}m\left(m-1\right){\left({\overline{\delta }}_i\right)}^{m-2}}\text{ (13a-b)}\\ \left\{\begin{array}{cc}>0& \text{implies }{\overline{\delta }}_i\text{ is local minimum,}\\ <0& \text{implies }{\overline{\delta }}_i\text{ is local maximum;}\end{array}\right.\end{array}$$

If there are several local minima/maxima then the lowest/highest is chosen as the overall minimum/maximum.

It may happen that the second order derivative vanishes and some higher-order derivatives vanish also. Not all derivatives up to order M can vanish otherwise the polynomial would reduce to a constant. Suppose that the first derivative which does not vanish at ${\overline{\delta }}_i$ is of order s; if s is odd the ${\overline{\delta }}_i$ is an inflexion point, not a maximum or a minimum (14a):

$$\begin{array}{l}{C}_{\alpha i}{}^{\prime }\left({\overline{\delta }}_i\right)=\mathrm{...}=C_{\alpha i}^{\left(s-1\right)}\left({\overline{\delta }}_i\right)=0\ne C_{\alpha i}^{\left(s\right)}\left({\overline{\delta }}_i\right)\text{ (14a,b)}\\ \left\{\begin{array}{cc}s\text{ is odd}& \text{implies }{\overline{\delta }}_i\text{ is an inflexion-point,}\\ s\text{ is even}& \text{ implies }{\overline{\delta }}_i\text{ is an extremum; }\end{array}\right.\end{array}$$

If s is even then ${\overline{\delta }}_i$ is an extremum (14b) and the sign decides if it is a maximum or minimum.

$$\begin{array}{l}{C}_{\alpha i}{}^{\prime }\left({\overline{\delta }}_i\right)=\mathrm{...}=C_{\alpha i}^{\left(2s-1\right)}\left({\overline{\delta }}_i\right)=0\ne C_{\alpha i}^{\left(2s\right)}\left({\overline{\delta }}_i\right)\text{ (15a,b)}\\ \left\{\begin{array}{cc}>0& \text{implies }{\overline{\delta }}_i\text{ is local minimum,}\\ <0& \text{implies }{\overline{\delta }}_i\text{ is local maximum}\text{.}\end{array}\right.\end{array}$$

All local maxima/minima, arising at second-order derivative (13a,b) or at any derivative s of higher even order (15a,b) are considered for the overall maximum and minimum:

$$C_{\alpha i\max }=\sup \left\{C_{\alpha i}\left({\overline{\delta }}_i\right)\right\}\ge \inf \left\{C_{\alpha i}\left({\overline{\delta }}_i\right)\right\}=C_{\alpha i\min }\text{ (16)}$$

If the deflection ${\overline{\delta }}_i$ lies outside the range of possible deflections then the corresponding extremum is at one of the deflection limits. The extrema for each decoupled control specify by addition the overall extrema.

High-order polynomials together with coupled controls

The optimization method applies most simply to decoupled controls specified by second-order polynomials. These two restrictions were relaxed to allow either coupled controls (6.1) or high-order polynomials (6.2). Next both constraints are removed, so that the controls can be coupled and specified by polynomials of any degree. If the highest degree is M, all polynomials can be written, possibly with some zero coefficients, in the form:

$$C_{\alpha i}=A_{\alpha i}+{\displaystyle \sum _{j=1}^N{A}_{\alpha ij}{\delta }_j}+{\displaystyle \sum _{j,k=1}^N{A}_{\alpha ijk}{\delta }_j}{\delta }_k+\mathrm{...}={\displaystyle \sum _{m=0}^M{\displaystyle \sum _{j_1,\mathrm{...},j_m=1}^N{A}_{\alpha i{j}_1\mathrm{...}{j}_m}{\delta }_{j_1}\mathrm{...}}{\delta }_{j_m}}\text{ (17)}$$

where: (i) The static values are unchanged; (ii) The slopes (18a) and curvatures (18b) are as before in the coupled case (14a,b).

$$a_{\alpha ij}=\frac{\partial C_{\alpha i}}{\partial {\delta }_j}=A_{\alpha ij},2b_{\alpha ijk}=\frac{{\partial }^2{C}_{\alpha i}}{\partial {\delta }_j\partial {\delta }_k}=2A_{\alpha ijk},\frac{{\partial }^m{C}_{\alpha i}}{\partial {\delta }_{j_1}\mathrm{...}\partial {\delta }_{j_m}}=m!A_{\alpha i{j}_1\mathrm{...}{j}_m}\text{ (18a-c)}$$

(iii) The higher-order derivatives (18c) may all be designated by the same letter A and distinguished by the number of indices $\left(j_1,\mathrm{...},j_m\right)$ for $0\le m\le M$.

Due to the coupling the extremum must be sought jointly for all controls together:

$$0=d{C}_{\alpha }={\displaystyle \sum _{i=1}^{N}d{C}_{\alpha i}}={\displaystyle \sum _{m=1}^{M}m{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j_1,\mathrm{...},j_m=1}^N{A}_{\alpha i{j}_1\mathrm{...}{j}_m}{\overline{\delta }}_{j_1}\mathrm{...}{\overline{\delta }}_{j_m}d{\delta }_{j_1}}}}\text{ (19)}$$

the roots of (19) specify the extrema. If the second variation is positive/negative the extremum is a minimum/maximum

$$d^2{C}_{\alpha }={\displaystyle \sum _{i=1}^N{d}^2{C}_{\alpha i}}={\displaystyle \sum _{m=1}^{M}m\left(m-1\right){\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j_1,\mathrm{...},j_m=1}^N{A}_{\alpha i{j}_1\mathrm{...}{j}_m}{\overline{\delta }}_{j_1}\mathrm{...}{\overline{\delta }}_{j_m}}}}d{\delta }_{j_1}d{\delta }_{j_2}$$

$$\left\{\begin{array}{cc}>0& \text{implies }{\overline{\delta }}_i\text{ is local minimum,}\\ <0& \text{implies }{\overline{\delta }}_i\text{ is local maximum;}\end{array}\right.\text{ (20a-c)}$$

this is equivalent to stating that the matrix (21a) is positive/negative definite, i.e. as all eigenvalues real and positive (negative)

$$X_{j_1{j}_2}={\displaystyle \sum _{m=2}^{M}m\left(m-1\right){\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j_1,\mathrm{...},j_m=1}^N{A}_{\alpha i{j}_1\mathrm{...}{j}_m}{\overline{\delta }}_{j_3}\mathrm{...}{\overline{\delta }}_{j_m}}}}$$

$$\left\{\begin{array}{c}\text{positive-definite implies local minimum,}\\ \text{negative-definite implies local maximum}\text{.}\end{array}\right.\text{ (21a-c)}$$

The matrix (21a) may not be definite, e.g. it may be indefinite, positive or negative semi-definite, i.e. have eigenvalues with opposite signs, or some zero eigenvalues; in this case ${\overline{\delta }}_i$ is not an extremum. If all eigenvalues of (21a) are zero, then it is necessary to proceed to higher order to know if ${\overline{\delta }}_i$ is an extremum.

If the differential (22a) of lowest order which does not vanish is of odd order (22b) then ${\overline{\delta }}_i$ is an inflexion, not an extremum:

$$\begin{array}{l}d{C}_{\alpha i}\left({\overline{\delta }}_{î}\right)=\mathrm{...}=d^{\left(s-1\right)}{C}_{\alpha i}\left({\overline{\delta }}_{î}\right)=0\ne d^{\left(s\right)}{C}_{\alpha i}\left({\overline{\delta }}_{î}\right)=X:\text{ (22a-d)}\\ \left\{\begin{array}{l}s\text{ is odd implies }{\overline{\delta }}_i\text{ is inflexion point,}\\ s\text{ is even }\left\{\begin{array}{cc}>0& \text{implies }{\overline{\delta }}_i\text{ is local minimum,}\\ <0& \text{implies }{\overline{\delta }}_i\text{ is local maximum;}\end{array}\right.\end{array}\right\}\end{array}$$

If the first non-vanishing differential is of even order then ${\overline{\delta }}_i$ is an extremum (22c,d) viz. a local minimum/maximum if it is always positive/negative. If X does not have a fixed sign then ${\overline{\delta }}_i$ is not an extremum. If the value ${\overline{\delta }}_i$ lies outside the range of possible deflections then the extremum is at one of the extreme deflections. The set of values ${\overline{\delta }}_i$ is then used to calculate the overall maximum and minimum in (17).

Data points for coupled/uncoupled controls of any order

The number of data points needed ${\text{Q}}_0$ is lowest (6) for the three forces and moments (total 6), for N decoupled control surfaces ($6\times N$), for second-degree polynomials with 3 coefficients each:

$${\text{Q}}_0\left(N\right)=6\times N\times 3=18N\text{ (23)}$$

If the controls remain decoupled but the polynomials are (10) of degree M, the 3 coefficients are replaced by M + 1, and the number of data points need is:

$${\text{Q}}_1\left(N,M\right)=6\times N\times \left(M+1\right)=6N\left(M+1\right)\text{ (24)}$$

this reduces to (23) for M = 2. In the case (3) of a polynomial of degree M = 2 and N coupled controls, there are 6N static values, $6N^2$ first-order derivatives and $6N^3$ second-order derivatives; the latter are symmetric (6a), reducing their number to $6N^2\left(N+1\right)/2$ in:

$$M=2:{\text{ Q}}_2\left(N\right)=6\left[N+N^2+N^2\left(N+1\right)/2\right]=3\left(2N+3N^2+N^3\right)\text{ (25)}$$

In the general case (17) of polynomials of degree M and N coupled controls for each force and moment there is one static value, $N^2$ slopes, $N^2\left(N+1\right)/2$ curvatures and

$$\begin{array}{l}m=1,2,\mathrm{...}:N\left(\begin{array}{c}N+m-1\\ m\end{array}\right)=\frac{\left(N+m-1\right)!N}{m!\left(N-1\right)!}\text{ (26a)}\\ =\frac{N^2\left(N+1\right)\left(N+2\right)\mathrm{...}\left(N+m-1\right)}{m!}\end{array}$$

coefficients of order m that are symmetric in all indices; the total number of data points is:

$$\begin{array}{l}{\text{Q}}_3\left(N,M\right)=6N\left\{1+N+N\left(N+1\right)/2+\mathrm{...}+N\mathrm{...}\left(N+M-1\right)/M!\right\}\text{ (26b)}\\ =6N\left\{1+{\displaystyle \sum _{m=1}^M\left(\begin{array}{c}N+m-1\\ m\end{array}\right)}\right\}\end{array}$$

For polynomials of second degree $M=2$ the number (27a) of data points (26b) agrees with (25), and it increases for polynomials of third degree to (27b):

$$\begin{array}{l}{\text{Q}}_3\left(N,2\right)={\text{Q}}_2\left(N\right){\text{; Q}}_3\left(N,3\right)=6N\left[\begin{array}{l}1+N+N\left(N+1\right)/2\\ +N\left(N+1\right)\left(N+2\right)/6\end{array}\right]\text{ (27a-b)}\\ =6N+11N^2+6N^3+N^4\end{array}$$

As can be seen in the Table 1 the number of data points needed increases rapidly with the degree of the polynomial, more so in the coupled case.

The interaction between control surfaces farther apart would be weaker, and could be neglected to reduce the number of data points needed. Suppose that there are N control surfaces each interacting only with its neighbors: (i) The first and last surfaces have each one neighbor, and thus one coefficient of degree zero, two of degree one $\left({\delta }_1,{\delta }_2\right)$, three of degree two $\left[{\delta }_1{}^2,{\delta }_2{}^2,{\delta }_1{\delta }_2\right]$, four of degree three $\left[{\left({\delta }_1\right)}^3,{\left({\delta }_1\right)}^3{\delta }_2,{\delta }_1{\delta }_2{}^2,{\left({\delta }_2\right)}^3\right]$, and $\left(m+1\right)$ of degree $m$; (ii) The $\left(N-2\right)$ control surfaces not at either end have two neighbors, and hence one coefficient of zero degree, three of first degree $\left({\delta }_1,{\delta }_2,{\delta }_3\right)$, six of second degree $\left[{\delta }_1{}^2,{\delta }_2{}^2,{\delta }_3{}^2,{\delta }_1{\delta }_2,{\delta }_1{\delta }_3,{\delta }_2{\delta }_3\right]$ and $\left(m+1\right)\left(m+2\right)/2$ coefficients of degree $m$; (iii) These coefficients add for all degrees from 0 to $M$, for each of three components of forces and moments:

$$\begin{array}{l}N\ge 2:{\text{ Q}}_4\left(N,M\right)=6\left\{2{\displaystyle \sum _{m=0}^M\left(m+1\right)+\left(N-2\right){\displaystyle \sum _{m=0}^M\left(m+1\right)\left(m+2\right)/2}}\right\}\text{ (28)}\\ =6\left(M+1\right)\left(M+2\right)+3\left(N-2\right){\displaystyle \sum _{m=0}^M\left(m+1\right)\left(m+2\right)}\end{array}$$

This is the number of data points in the case of N control surfaces coupled only to the nearest neighbor, and polynomial of degree M. For two control surfaces the number of parameters is: (i) The same for neighboring interaction (28) or all interactions (26b); (ii) Larger than for decoupled controls (24):

$$\begin{array}{l}{\text{Q}}_4\left(2,M\right)=6\left(M+1\right)\left(M+2\right)=12{\displaystyle \sum _{m=0}^M\left(m+1\right)=12{\displaystyle \sum _{m=0}^M\left(\begin{array}{c}m+1\\ m\end{array}\right)}}\text{ (29)}\\ ={\text{Q}}_3\left(2,M\right)>12\left(M+1\right)={\text{Q}}_1\left(2,M\right)\end{array}$$

For more than two control surfaces (30a), the number of parameters for neighboring interaction (28) is: (i) Larger than (24) for decoupled controls (30b):

$$\text{N}\ge {\text{3: Q}}_4\left(N,M\right)>\left(M+1\right)\left[12+6\left(N-2\right)\right]=6N\left(M+1\right)={\text{Q}}_1\left(N,M\right)\text{ (30a,b)}$$

(ii) Smaller than (26b) for all controls coupled (30c,d):

$$\begin{array}{l}N\ge 3:{\text{ Q}}_4\left(N,M\right)<6\left(N-2\right){\displaystyle \sum _{m=0}^M\left(m+1\right)\left(m+2\right)=}6\left(N-2\right){\displaystyle \sum _{m=0}^M\left(\begin{array}{c}m+2\\ 2\end{array}\right)}\\ <6N{\displaystyle \sum _{m=0}^M\left(\begin{array}{c}m+2\\ m\end{array}\right)\le 6N{\displaystyle \sum _{m=0}^M\left(\begin{array}{c}N+m-1\\ m\end{array}\right)}}<{\text{Q}}_3\left(N,M\right).\text{ (30c-d)}\end{array}$$

In the case of polynomials of degree two (31a) and three (31b) the number of parameters for neighboring interaction:

$$M=2;N\ge 2:{\text{ Q}}_4\left(N,2\right)=72+60\left(N-2\right)=60N-48\text{ (31a)}$$

$$M=3;N\ge 2:{\text{ Q}}_4\left(N,3\right)=120+120\left(N-2\right)=120\left(N-1\right)(31b)$$

is indicated in Table 1 in comparison with decoupled (24) and fully coupled (25,27) controls. The case of each control surface interacting only with its neighbor(s) reduces significantly the number of data points needed, and should account for control coupling with good accuracy. Since the method applies both to coupled and uncoupled controls, and polynomials of any degree, it can be illustrated for the simplest case, for which data is more readily available.

Initial Condition an Optimal Deflection

Before proceeding to implement optimal pitch trim strategies, it is useful to start with some simple initial pitch trim conditions, for three reasons: (i) They provide a more direct understanding of cruise equilibrium conditions; (ii) They serve as a starting point for the iterative optimisation process; (iii) They may suggest sub-optimal and non-optimal strategies which are may be simpler but still quite effective. For a given cruise condition, the effect on drag due to pitch trim is compared for three simple cases, viz.: (i) Equal deflection of all control surfaces (strategy I in 7.1); (ii) Deflection of elevator alone (strategy II corresponding to strategy A in [68]); (iii) Preferential deflection of inner control surfaces with moderate upper limit (strategy III in 7.2). The optimal deflection using Lagrange multipliers use two distinct initial conditions: (a) Deflection of elevator alone (strategy IV corresponding to strategy B in [68]); (b) Equal deflection of all control surfaces (strategy V in 7.3).

Equal deflection of all trailing edge surfaces

Consider a BWB aircraft configuration at a cruise weight W = 715 t, intermediate between initial and final cruise weights. At cruise altitude z = 35 kft the sound speed is $c=295m.s^{-1}$, and the cruise Mach number $Ma=0.85$ corresponds to an indicated airspeed $U=Ma\times c=251m.s^{-1}$. At the tropopause the mass density is ρ = 0.223 kg m^-3, and thus the dynamic pressure is $q=\frac{1}{2}\rho U^2=7.025\times {10}^{3}kg{m}^{-1}{s}^{-2}$. For a reference wing area S = 961.35 m², this corresponds to a cruise lift coefficient:

$$C_L=2W/\rho S{U}^2=W/qS=\mathrm{0.10588.}\text{ (32)}$$

The lift coefficient C_L, and also the drag C_D and pitching moment C_M coefficients, are given in Table 2 for the chosen BWB aircraft configuration in a typical cruise condition. Linear interpolation of the values of the lift coefficient between zero α = 0° and three degree α = 3° AOA, shows from Table 2 that (25) corresponds to a cruise AOA

α₀ = 0.71789°.      (33)

Further linear interpolation in the Table 2 shows that this AOA corresponds to a cruise drag coefficient (34a):

C_D = 0.00569, C_M = - 0.02441,      (34a,b)

and pitching moment coefficient (34b). The total dynamic force $\overline{q}=qS=6.7535\times {10}^{6}N,$ then leads to a cruise drag $D=C_D\overline{q}=3.8427\times {10}^{4}N$ and pitching moment $M=C_M\overline{q}\overline{c}=-5.2699\times {10}^6$ N m. The cruise lift-to-drag ratio is L/D = C_L/C_D = 18.6.

There are five sets i = 1,...,5 control surfaces available for pitch control whose areas are indicated in Table 3 together with the fraction of wing area S_i/S, and fraction of total control surface are S_i/S₀, where:

$$S_0\equiv {\displaystyle \sum _{i=1}^5{S}_i}.\text{ (35)}$$

The lift C_Li, drag C_Di and pitching moment C_Mi coefficients for each surface i = 1,...,5, and those for all surfaces together i = 0, are given in Table 4 for upward or downward deflections of three degrees δ_i = ± 3°, at angles of attack α = 0° and α = 3°. From these are interpolated the values at cruise AOA α₀ = 0.71789° indicated in the same Table 4. The first and second-order derivatives of the aerodynamic coefficients are calculated applying finite differences to the values in Table 4 leading to the results in Table 5.

The preceding tables contain all the data needed to implement various trimming strategies. The pitching moment coefficient at cruise (34b), must be balanced by the opposite trimming pitching moment, e.g. adopting the strategy I of equal deflection δ_I of all trailing-edge control surfaces (36a):

$C_{MR}\equiv 0.02441=C_{M0}\left({\delta }_I\right)\Rightarrow {\delta }_I=4.4680º\equiv {\delta }_{Ii},\text{ (36a,b)}$

then linear interpolation in Table 5 leads to the deflection (36b) indicated in the first column of Table 6. Since the latter deflection is small, the use of linear aerodynamics and linear interpolation is justified. The deflection (36b) leads from Table 4 to a drag coefficient (37a):

$C_{DI}\equiv C_{DO}\left({\delta }_I\right)=0.00659,\Delta C_{DI}\equiv C_{DI}-C_D=0.00089,\text{ (37a,b)}$

which exceeds the cruise drag coefficient in Table 1 by 89 drag counts. Thus there is a 15.6% drag increase:

$\Delta C_{DI}/C_D=0.156,\text{ (38)}$

by adopting the strategy I of pitch trim by equal deflection of all control surfaces. This is a relatively large cruise drag penalty to achieve pitch trim, so another alternative is sought.

The strategy I of equal deflections δ_I of all control surfaces is unlikely to be good, because it does not exploit the differences between the control surfaces, in their ability to produce pitching moment and reduce drag. It is seen from Table 5, that the centerbody elevator has: (i) One of the largest positive pitching moment slopes, hence can trim the aircraft with smaller deflections; (ii) Has the largest (in modulus) negative drag slope, so that drag is reduced from small deflections. Thus suggests that the preceding strategy I be compared next with the strategies of maximal deflection of the inboard control surfaces. The strategy II of deflecting only the innermost trailing-edge control surface, namely the central body elevator was considered as strategy A before [68], leading to a large elevator deflection shown in the second column of Table 6. A large elevator deflection could have undesirable consequences, e.g. shock wave formation and boundary layer separation, or exciting aeroelastic modes and causing earlier onset of buffet. Thus it may be necessary to limit the maximum deflection of all control surfaces to a given value, say 7.5º. In this case the elevator deflection is limited, and control surfaces further outboard must be used, in strategy III until the required pitching moment is obtained.

Preferential deflection of inboard surfaces

In the strategy III, the body elevator is limited to say, a seven-and-a-half degree deflection (39a) to avoid aerodynamic, aeroelastic or other problems:

δ_III1 = 7.5º, CMIII1 = CM1 (δ_III1) = 0.01828,    (39a,b)

the resulting pitching moment coefficient (39b) falls short of the required value (36a) by (40):

$\Delta C_{MIII1}\equiv C_{MR}-C_{MIII1}=\mathrm{0.00560.}\text{ (40)}$

Thus the strategy III of limiting the deflections to 7.5°, requires more than the elevator for pitch trim, as could be expected from the second column of Table 6 showing that the elevator alone would require a 9.0° deflection for pitch trim. The short-fall (40) ≡ (41a) in pitch trim would be covered by the outer elevator:

$0.00560=\Delta C_{MIII1}=C_{M2}\left({\delta }_{III2}\right)=\delta {}_{{}_{III2}}=12.055º,\text{ (41a,b)}$

deflecting by (41b), which exceeds the 7.5° limit. Enforcing the latter limit for the outer elevator (43a):

δ_III 2 = 7.5°, CMIII2 = CM2 (δ_III2) = -0.00400,   (42a,b)

leads to a negative contribution to the pitching moment (42b), so that the shortfall is now higher:

$\Delta C_{MIII2}=\Delta C_{MIII1}-C_{MIII2}=\mathrm{0.00960.}\text{ (43)}$

This shortfall is not compensated by the inner flap at the maximum allowed deflection:

δ_{III 3} = 7.5°, C_{M III 3} = C_{M 3} (δ_{III 3}) = 0.00536,    (44a,b)

and the remaining shortfall (45a):

0.00424 = Δ _{M III 2} – C_{M III 3} = Δ C_{M III 3} = C_{M III 4} = C₄ (δ_{III 4}),    (45a)

is covered by deflecting the outer flap by (45b):

δ_{III 4} = 3.5102°; δ_{III 5} = 0°,      (45b,c)

thus the ailerons need not be deflected. Thus the strategy III of preferential deflection of inboard control surfaces, not exceeding the 7.5° limit, leads in the third column of Table 6 to the maximum deflections of the elevators (39a,42a) and inner flap (44a), smaller deflection of the middle flap (45b) leaving only the ailerons (45c) unused.

The Table 5 specifies drag coefficients corresponding to these deflections (46a-e):

$$C_{DIII1}=C_{D1}\left(7.5º\right)=0.00404+0.000016\times {7.5}^2=0.00494,\text{ (46a)}$$

$$C_{DIII2}=C_{D2}\left(7.5º\right)=0.00531+0.0000022\times {7.5}^2=0.00543,\text{ (46b)}$$

$$C_{DIII3}=C_{D3}\left(7.5º\right)=0.00531+0.000013\times {7.5}^2=0.00604,\text{ (46c)}$$

$C_{DIII4}=C_{D4}\left(3.5º\right)=0.004615,\text{ (46d)}$

$C_{DIII5}=C_{D5}\left(0º\right)=0.00569,\text{ (46e)}$

where curvature correction was applied, for the first three deflections, which are larger. They are multiplied by the fraction of the total control surface area in Table 3, to give the trimmed drag:

$$C_{DIII}={\displaystyle \sum _{i=1}^5{C}_{DIIIi}{S}_i/S_0}=0.00570,\text{ (47)}$$

which leads to a trimmed drag a little higher than the untrimmed drag (48a):

Δ C_{D III} ≡ C_{D III} – C_D = 0.00001,     Δ C_{D III} / C_D = 0.0018,    (48a,b)

corresponding to 1 drag counts or a 0.2% penalty. The three non-optimal cruise pitch trim strategies are compared in Table 6: (i) The strategy I of equal collective deflection of all trailing-edge control surfaces leads to a 89 counts of drag as penalty; (ii) The drag count penalty is reduced to 1 by the strategy III of preferential deflection of inboard control surfaces with a 7.5° degree limit; (iii) The most elementary strategy II of elevator deflection alone gives a cruise drag reduction of 16 counts due to pitch trim. The result that the classical strategy II is the best so far from the point of view of drag, need not to be general, and could be a consequence of the particular aerodynamic data used in the present calculation.

Influence of initial condition for finite iterations

The optimal strategy, after convergence, should lead to the same optimal deflections, for any initial condition. If, however, as is always the case in practice, a finite number of iterations is used, the iterated 'optimal' deflections will depend on the initial condition. The optimal strategy IV with four iterations starting with the non-optimal strategy II of elevator deflection alone corresponding to strategy B in [68], is compared next with the optimal strategy V with six iterations starting with the non-optimal strategy I of equal control surface deflections (7.1). The former strategy IV was shown in Table 6 in [68], and the latter strategy is shown in Table 7, where the calculations were performed with more digits in the first than in the second case. The optimal deflections for the latter strategy V:

$${\delta }_{Vi}\equiv \left[{\delta }_i^{\left(6\right)}+{\delta }_i^{\left(5\right)}\right]/2=\left\{4.125º,0.02º,1.88º,0.01º,-3.685º\right\},\text{ (49)}$$

are smaller than for strategy IV.

The distinct deflection for strategies IV and V, lead to different drag coefficients for the latter, from Table 2, viz.:

$$C_{DV1}\equiv C_{D1}\left(4.125º\right)=0.00618,\text{ (50a)}$$

$$C_{DV2}\equiv C_{D2}\left(0.002º\right)=0.00776,\text{ (50b)}$$

$$C_{DV3}\equiv C_{D3}\left(1.68º\right)=0.00768,\text{ (50c)}$$

$$C_{DV4}\equiv C_{D4}\left(0.01º\right)=0.00846,\text{ (50d)}$$

$$C_{DV5}\equiv C_{D5}\left(-3.685º\right)=\mathrm{0.00803.}\text{ (50e)}$$

The corresponding total drag (79a).

$$C_{DV}=0.00770,A{C}_{DV}\equiv C_{DV}-C_D=0.00201,\text{ (51a,b)}$$

is 201 drag counts above (51b) the untrimmed value, for a 35.3% cruise drag penalty. From the latter it is clear that the 'optimal' deflections after 4 accurate iterations with a good initial value, give better results than six less accurate iterations starting with a worse value. The comparison of drags obtained by the methods I to V could be misleading because they correspond to different lifts, and hence to distinct flight conditions, such as different speed, altitude or both. A valid comparison of all strategies requires that pitch trim be achieved with the same lift (8).

Pitch Trim with Constant Lift

The three pitch trim strategies I, II and VI are considered with constant lift, thus leading to modification of the strategies: (I) Of equal deflection of all trailing edge surfaces (8.1); (II) Of deflection of the centerbody elevator only (8.2); (VI) equipartition of the cruise lift contribution from each control surface (8.3).

Effect of pitch trim on lift in cruise

The strategy I of equal deflection of all control surfaces is applied using the following procedure, which finds directly the equilibrium of lift, drag and pitching moment in cruise. The lift coefficient depends on AOA α, and for pitch trim strategy I on the collective angle of deflection δ_I for all control surfaces. For a given weight, altitude and airspeed, the lift coefficient cannot change, i.e. it takes the value (32); then must hold for small angles:

0.10588 = C_L = 0.04411 + α C_{L α} + δ_I $C_{L{\delta }_0}$,      (52)

where the derivatives are calculated at zero angles α = 0° = δ_I, viz. (47a) from Table 2:

$$\begin{array}{l}{C}_{L\alpha }={\left(\partial C_L/\partial \alpha \right)}_{{\delta }_0=0}=\left[C_L\left(\alpha =3º\right)-C_L\left(\alpha =0º\right)\right]/3º\text{ (53a)}\\ =\left(0.30224-0.04411\right)/3º=0.086043,\end{array}$$

$$\begin{array}{l}{C}_{L{\delta }_0}={\left(\partial C_{L0}/\partial {\delta }_0\right)}_{{\alpha }_0=0}=\left[C_{L0}\left({\delta }_0=+3º\right)-C_{L0}\left({\delta }_0=-3º\right)\right]/6º\text{ (53b)}\\ =\left(0.15977-0.49675\right)/6º=-0.056163,\end{array}$$

and (47b) from Table 4. It follows that for constant lift, the AOA α and collective control surface deflection must be related by:

δ_I = 1.5320 α_I - 1.0998, α_I = 0.65273 δ_I + 0.71787,     (54a,b)

allowing an infinite choice of one parameter.

In the same small angle approximation, the pitching moment coefficient is given by:

$C_M\left(\alpha ,\delta \right)=C_M\left(0,0\right)+\alpha C_{M\alpha }+{\delta }_I{C}_{M{\delta }_I}.\text{ (55)}$

At constant lift (54a,b) it depends only on one parameter, e.g. AOA:

$C_M\left(\alpha \right)=-0.00819-0.02259{\alpha }_I+0.028935\left(1.5320{\alpha }_I-1.0998\right),\text{ (56)}$

where C_Mα was calculated from Table 2 and C_Mδ from Table 4. For pitch trim the pitching moment coefficient must be zero, leading to the angle of attack (57a):

$$C_M\left({\alpha }_I\right)=0:{\alpha }_I=1.8406º,{\delta }_I=1.7200º,\text{ (57a,b)}$$

and collective control surface deflection (57b). The drag coefficient cannot be accurately predicted by a small angle approximation such as:

$$C_D\left(\alpha ,\delta \right)=C_D\left(0,0\right)+\alpha C_{D\alpha }+\delta C_{D\delta },\text{ (58a)}$$

and thus a different method is used as shown in Table 8: (i) The values of the drag coefficient in Table 4 are interpolated for the AOA (57a), for fixed deflections $\delta =\pm 3º;$ (ii) Then the values in Table 8 are extrapolated for the deflection (57b):

$C_{DI}^{*}=C_{D0}\left({\delta }_I\right)=C_{D0}\left(1.7200º\right)=\mathrm{0.00766.}\text{ (58b)}$

Thus the strategy I with cruise lift equilibration leads to a drag penalty (59a) or 197 counts, or 34.5% in (59b):

$\Delta C_{DI}=C_{DI}^{*}-C_D=0.00197,\Delta C_{DI}/C_D=\mathrm{0.345.}\text{ (59a,b)}$

Since the deflection of control surfaces upwards (51b) decreases lift, the AOA is increased (57a), and hence also the drag, as shown on Table 9. In the case of the strategy I of equal deflection of all control surfaces, the condition of cruise lift equilibration causes trim drag penalty of 197 drag counts. The opposite will be shown next for the strategy II of elevator deflection only, when the cruise lift equilibration condition decreases the pitch trim drag by 18 counts, as shown next.

A direct, non-iterative simultaneous approach

The direct, non-iterative approach to simultaneous determination of AOA and control surface deflection, used for strategy I in 7.1, applies also to other strategies, as shown next. For comparison, consider the decrease in cruise drag due to pitch trim is calculated next for strategy II of deflection of the centerbody elevator alone. Using (53a) and:

$C_L{{}_{\delta }}_1\equiv {\left(\partial C_{L1}/\partial {\delta }_1\right)}_{\alpha =0}=-0.011245,\text{ (60)}$

from Table 4, the condition (52) of no lift change is now replaced by:

${\delta }_{II}=7.6517{\alpha }_{II}-\mathrm{5.4931.}\text{ (61)}$

The larger values in (61) compared to (54a), are due to deflecting only one surface instead of all by the same amount. Using the analogue of (55) for pitch trim:

$\begin{array}{l}0=C_M({\alpha }_{II})=-0.00819-0.02259{\alpha }_{II}+0.0053067\text{ (62)}\\ \times (7.6517{\alpha }_{II}-5.4931),\end{array}$

leads to the AOA (63a):

${\alpha }_{II}=2.0727°,{\delta }_{II}=10.367°,\text{ (63a,b)}$

and elevator deflection (63b), from (61).

The drag is again interpolated from Table 2 to the AOA (63a), for fixed deflection ${\delta }_{II}=\pm 3°$ as shown in Table 6, leading to:

$C_{DII2}^{*}=C_{D1}({\delta }_{II})=0,00319,\text{ (64a)}$

which is very low because $\partial C_{DII}/\partial {\delta }_{II}<0,$ leading to a large reduction for large ${\delta }_{II}.$ It is not reasonable to assume constant slope, i.e. neglect curvature effects, for large ${\delta }_{II}$. Thus a curvature correction made to (64a), viz.:

$$C_{DII2}^{*}=0.00319+\frac{1}{2}{C}_{D2}^{"}{\left({\delta }_{II}\right)}^2=0.00491,\text{ (64b)}$$

where $C_{D2}^{"}$ = 0.000032 from Table 5. The non-deflected surfaces i = 2, 3, 4, 5 influence drag and thus the total drag is now:

$C_{DII}^{*}\equiv C_{DII1}^{*}{S}_1/S_0+C_{DIIi}^{*}\left(1-S_1/S_0\right)=\mathrm{0.00551.}\text{ (65a)}$

The strategy II of elevator deflection only, with cruise lift equilibrium, leads to a drag reduction due to pitch trim (65b) of 18 counts or -3.2% in (65c):

$$\Delta C_{DII}^{*}\equiv C_{DII}^{*}-C_D=-0.00018,\Delta C_{DII}^{*}/C_D=-\mathrm{0.032.}\text{ (65b,c)}$$

After showing the effect of the cruise lift equilibrium condition on the worst (I) and best (II) non-optimal pitch trim strategies, it is worthwhile to consider a non-optimal pitch trim strategy VI, for which cruise lift equilibration is taken as the starting point.

Equipartition of cruise lift contributions

A more direct strategy VI, is to conserve the total lift coefficient:

$0.10588=C_L=0.04411+\alpha C_{L_{\alpha }}+{\displaystyle \sum _{i=1}^5{\delta }_i}C{\text{'}}_{Li},\text{ (66)}$

taking equal contributions from each control surface:

$0.012338=0.2\alpha C_{L\alpha }+{\delta }_{Vi}C{\text{'}}_{Li}.\text{ (67)}$

It follows that the deflections are related to the AOA by:

$${\delta }_{VI1}=-1.0724+1.49575\alpha ,\text{ (68a)}$$

$${\delta }_{VI2}=-3.5001+4.88189\alpha ,\text{ (68b)}$$

$${\delta }_{VI3}=-1.2609+1.7581\alpha ,\text{ (68c)}$$

$${\delta }_{VI4}=-6.86971+9.5817\alpha ,\text{ (68d)}$$

$${\delta }_{VI5}=-2.473+3.45105\alpha ,\text{ (68e)}$$

using (59a) and taking $C{\text{'}}_{Li}$ at ${\delta }_i=0$ from Table 5; the pitching moment:

$$C_M=-0.00819-0.02259{\alpha }_{IV}+{\displaystyle \sum _{i=1}^5{\delta }_{IVi}{C}_{Mi}^{\text{'}}},\text{ (69)}$$

vanishes at the trim conditions:

$$0=C_M=-0.00819-0.02259{\alpha }_{IV}\text{+ 0}\text{.00546 (1}\text{.49575}{\alpha }_{IV}\text{ -1}\text{.072)}+$$

$$+0.0015185\left(4.8819{\alpha }_{IV}-3.5001\right)+0.004075\left(1.7587{\alpha }_{IV}-1.2609\right)+\text{ (70)}$$

$$+0.0087615\left(9.5817{\alpha }_{IV}-6.8697\right)+0.003297\left(3.45105{\alpha }_{IV}-2.4743\right),$$

where $C_{Mi}^{\text{'}}$ were taken at ${\delta }_i=0$ from Table 5. The trim condition corresponds to (71a) the AOA:

$${\alpha }_{IV}=2.2794º,{\delta }_{IVi}=\left\{6.6990º,7.62770º,2.7478º,14.971º,5.3920º\right\},\text{ (71a,b)}$$

and the corresponding (68a-e) deflections are (71b).

The drag coefficients are given in Table 8 for the AOA (71a) and two deflections ${\delta }_i=\pm 3º$, based on Table 4; extrapolations for the deflections (71b), leads to the drag coefficients:

$$C_{DVI1}\equiv C_{D1}\left({\delta }_{IV1}\right)=0.00529+\frac{1}{2}{C}_{D1}^{"}{\left({\delta }_{IV1}\right)}^2=0.00601,\text{ (72a)}$$

$$C_{DVI2}\equiv C_{D2}\left({\delta }_{IV2}\right)=0.00727+C_{D2}^{"}{\left({\delta }_{IV2}\right)}^2=0.00730,\text{ (72b)}$$

$$C_{DVI3}\equiv C_{D3}\left({\delta }_{IV3}\right)=0.00809+C_{D3}^{"}{\left({\delta }_{IV3}\right)}^2=0.00818,\text{ (72c)}$$

$$C_{DVI4}\equiv C_{D3}\left({\delta }_{IV4}\right)=0.00640+C_{D4}^{"}{\left({\delta }_{IV4}\right)}^2=0.01660,\text{ (72d)}$$

$$C_{DVI5}\equiv C_{D5}\left({\delta }_{IV5}\right)=0.00913+\frac{1}{3}{C}_{D5}^{"}{\left({\delta }_{IV5}\right)}^2=0.00936,\text{ (72e)}$$

where the curvature corrections were applied using values from Table 5:

$C_{Di}^{"}=\left\{0.0000323,0.00000133,0.0000257,0.0000910,0.0000156\right\}.\text{ (73)}$

The large deflections (71b), lead to relatively large drag coefficients (72a-e) which are weighted by the relative control surface areas in Table 3, to yield the total drag coefficient:

$$C_{DVI}={\displaystyle \sum _{i=1}^5{C}_{DVI}\left(S_i/S_0\right)}=0.01089;\text{ (74)}$$

this leads to a trim drag penalty of 520 counts (75a) or 91% in (75b):

$$\Delta C_{DVI}\equiv C_{DVI}-C_D=520,\Delta C_{DVI}/C_D=\mathrm{0.914.}\text{ (75a,b)}$$

As shown in Table 9 there (75a,b) can be a large difference in trim drag according to pitch trim strategy, suggesting that optimal deflections to minimize cruise drag should be considered.

Sub-Optimal and Simplified Trim Strategies

The double iteration loops needed to make optimal deflections (8.1-8.2) compatible with cruise lift equilibrium (8.3), can be avoided by sub-optimal strategies. A sub-optimal strategy uses optimal values in a non-optimal way, e.g. in the sub-optimal strategy VII, the optimal deflections (8.1-8.2) are multiplied by a constant, which is specified by the condition of cruise lift equilibrium (9.1). The ideas arising from optimal strategies may be used in simplified strategies, which are much more effective with less labour, e.g. the strategy of deflecting differently two distinct group of control surfaces, in two ways (strategies VIII and IX) as to reduce drag while producing the required pitching moment for each of them (9.2). This idea is further refined an strategy X, which deflects not all control surfaces, but only the two most effective in producing pitching moment with drag reduction (9.3).

Multiples of deflection and cruise equilibrium

The optimal deflections can be the used in a non-optimal may to specify a simpler sub-optimal strategy VII, which multiplies the deflections by a constant k, leading to the condition of constant lift (46) in the form:

$0.10588=C_L=0.04411+\alpha C_{L\alpha }+k{\displaystyle \sum _{i=1}^5{\delta }_i{C}_{Li}};\text{ (76a)}$

using (69a) and the second set of optimal deflections (63) leads to:

$${\displaystyle \sum _{i=1}^5{\delta }_{VIIi}}C{\text{'}}_{Li}=-0.047728;\text{ (76b)}$$

(72a,b) together with (33a) specify the ratio of deflections k in terms of the AOA:

$$k=1.8027{\alpha }_{VII}-\mathrm{1.2942.}\text{ (76c)}$$

The corresponding pitching moment coefficient (49) is given by:

$$C_M=-0.00819-0.02259{\alpha }_{VII}+k{\displaystyle \sum _{i=1}^5{\delta }_{VIIi}}{C}_{Mi}^{\text{'}},\text{ (77a)}$$

where from (83a) and (77):

$${\displaystyle \sum _{i=1}^5{\delta }_{VIIi}}{C}_{Mi}^{\text{'}}=0.018152;\text{ (77b)}$$

using (83b) the condition of pitch trim is:

$$C_M=0=-0.00819-0.02259{\alpha }_{VII}+0.018152k.\text{ (77c)}$$

The two conditions of (i) constant lift and (ii) pitch trim are satisfied substituting (76c) in (77c):

$$0.00819+0.02259{\alpha }_{VII}=0.018152\left(1.8027{\alpha }_{VII}-1.294\right),\text{ (78)}$$

which specifies the AOA (89a):

$${\alpha }_{VII}=3.1267º,k=4.3424,\text{ (79a,b)}$$

and coefficient (89b) for the final deflection angles:

$${\delta }_{VIIi}=k{\delta }_{Vi}=\left\{17.912º,0.0868º,8.1637º,0.0434º,-16.002º\right\}.\text{ (80)}$$

The drag coefficients are calculated from Table 4 for the AOA (89a) and listed in Table 8 for the deflections δ = ±3°. From this Table 8 the drag coefficients can be interpolated for the deflections (90), viz.:

$$C_{DVII1}=C_{D1}\left(17.912º\right)=-0.00137+0.000016\times {17.912}^2=0.00376,\text{ (81a)}$$

$$C_{DVII2}=C_{D2}\left(0.0868º\right)=0.01055,\text{ (81b)}$$

$$C_{DVII3}=C_{D3}\left(8.1637º\right)=0.00672+0.000013\times {8.1637}^2=0.00758,\text{ (81c)}$$

$$C_{DVII4}=C_{D4}\left(0.0434º\right)=0.01155,\text{ (81d)}$$

$$C_{DVII5}=C_{D5}\left(-16.002º\right)=0.01237+0.000008\times {16.002}^2=0.01442;\text{ (81e)}$$

the drag coefficient weighted by the fraction of control surface area in Table 3:

$$C_{DVII}={\displaystyle \sum _{i=1}^1{C}_{DVIIi}}{S}_i/S_0=0.00635,\text{ (82)}$$

leads to a 66 counts cruise drag penalty of 66 counts (93a):

$$\Delta C_{DVII}\equiv C_{DVII}-C_D=0.00066,\Delta C_{DVII}/C_D=0.116,\text{ (83a,b)}$$

corresponding to 11.6% more drag (93b). This is shown in Table 10, which has a similar format to Table 9. It is seen from Table 10 that the sub-optimal strategy VII, of non-optimal use of optimal deflections from strategy V, improves over strategy V, but not over the better initial condition in strategy IV. This result is not surprising, since it has been shown that pitch trim is compatible with cruise drag reduction. The optimal strategy IV may not be the best in practice, if parameter limitations prevent from reaching the optimum; in the present case the deflections are limited to small values and the aerodynamic coefficients, and their first-and second-order derivatives, have a limited range of variation. The best results obtained so far were for a simpler non-optimal strategy of elevator deflection only. This result could be due to the linearized aerodynamic data used. In general, a simple non-optimal strategy can give good results if it incorporates the lessons learned from optimal strategies, as suggested by strategy IV, which is further improved next.

Deflection direction determined by drag slope

It is seen from Table 10 that for, the best optimal strategy IV and the sub-optimal strategy VII, the inboard and outboard control surfaces deflect in opposite directions. This is confirmed from Table 11 which shows that: (i) The aileron is the only surface with positive drag slope, meaning that a drag reduction corresponds to a small downward deflection; (ii) Conversely, for all the other surfaces, the drag slope is negative, and thus drag reduces for small upward deflections:

${\delta }_{-}\equiv {\delta }_5<0<{\delta }_4={\delta }_3={\delta }_2={\delta }_1\equiv {\delta }_{+}.\text{ (84)}$

The strategy VIII deflects downwards by the same amount ${\delta }_{-}$ all surfaces with positive drag slope and deflects upward by the same amount ${\delta }_{+}$ all surfaces with negative drag slope, so as to reduce the drag for all control surfaces as shown by the example (94).

The condition of constant lift (60) for (94) is:

$0.06177=\alpha C_{L\alpha }+{\delta }_{-}{C}_{L5}^{\text{'}}+{\delta }_{+}{\displaystyle \sum _{i=1}^4{C}_{Li}^{\text{'}}},\text{ (85a)}$

where may be substituted (47a) and (81a), viz.:

$$0.06177=0.086043{\alpha }_{VIII}-0.0049865{\delta }_{-}-0.042775{\delta }_{+}.\text{ (85b)}$$

The condition (63) of pitch trim is:

$0=C_M=-0.00819-0.02259\alpha +{\delta }_{-}C{\text{'}}_{M5}+{\delta }_{+}{\displaystyle \sum _{i=1}^4{C}_{Mi}^{\text{'}}},\text{ (86a)}$

where (83a) may by substituted:

$$0.00819+0.02259{\alpha }_{VIII}=0.0032{\delta }_{-}+0.019815{\delta }_{+}.\text{ (86b)}$$

If the strategy VIII is adopted of keeping the AOA at the initial untrimmed value ${\alpha }_{VII}=0.71789º={\alpha }_0,$ in (26a) then deflections satisfy:

$$0.4934{\delta }_{VIII}{}_{-}+0.31223{\delta }_{VIII+}=0,\text{ (87a)}$$

$$0.003279{\delta }_{VIII}{}_{-}+0.019642{\delta }_{VIII+}=0.024407;\text{ (87b)}$$

it follows that the deflections:

$${\delta }_{VIII}{}_{-}=+24.727º<0<-2.8825º={\delta }_{VIII}{}_{+},\text{ (88a,b)}$$

are large for the ailerons (88a) and smaller for the other control surfaces (88b), and of opposite sign to what was required (84) for low drag. Thus trying to achieve trim at untrimmed AOA (26a), leads to unfavourable control surface deflections, in the sense that pitch trim is obtained by increasing drag. This is confirmed from the drag coefficients in Table 4 for the AOA (26a), viz.:

$$C_{DVIII1}\equiv C_{D1}\left({\delta }_{VIII}{}_{+}\right)=C_{D1}\left(2.8825º\right)=0.00661,\text{ (89a)}$$

$$C_{DVIII2}\equiv C_{D2}\left({\delta }_{VIII}{}_{+}\right)=C_{D2}\left(2.8825º\right)=0.00587,\text{ (89b)}$$

$$C_{DVIII3}\equiv C_{D3}\left({\delta }_{VIII}{}_{+}\right)=C_{D3}\left(-2.8825º\right)=0.00587,\text{ (89c)}$$

$$C_{DVIII5}\equiv C_{D5}\left({\delta }_{VIII}{}_{-}\right)=C_{D5}\left(24.727º\right)+0.000008\times 24.7272=0.00856,\text{ (89e)}$$

which lead by (43a) and Table 2 to a total drag coefficient (90a):

$$\begin{array}{l}{C}_{DVIII}=0.00551,\Delta C_{DVIII}=C_{DVIII}-C_D=0.00082,\text{ (90a-c)}\\ \Delta C_{DVIII}/C_D=0.144,\end{array}$$

corresponds to a large drag increase of 82 counts in (90b) or 14.4% in (90c), as shown in Table 12.

Allowing an AOA larger than the untrimmed value (26a), could lead to control surface deflections satisfying (84), and hence less control drag; this might overcome the extra drag due to increased angle of attack. Thus (85b) and (86b) are now solved for the control surface deflections δ±, without restriction on AOA, leading to:

${\delta }_{-}=37.287-17.495{\alpha }_{VII},\text{ (91a)}$

${\delta }_{+}=5.7751+4.0510{\alpha }_{VII}.\text{ (91b)}$

For pitch trim without change of AOA α_VIII = 0.71789° in (26a), from (91a,b) would follow (88a,b). No deflection of the inner control surfaces would be needed for the AOA:

$${\delta }_{+}=0:{\alpha }_{+}=5.7751/4.0510=1.4256º,\text{ (92a)}$$

$${\delta }_{-}\left({\alpha }_{+}\right)=037.287-17.495x1.4256º=12.346º;\text{ (92b)}$$

the positive aileron deflection would lead to a drag increase though. Instead, the strategy IX is adopted, of choosing the AOA so that no aileron deflection is needed:

$${\delta }_{IX-}=0:{\alpha }_{IX}=37.287/17.495=2.1313º;\text{ (93a)}$$

the deflection of the inner surfaces is now positive:

$${\delta }_{IX+}\equiv {\delta }_{+}\left({\alpha }_{IX}\right)=-5.7751+4.0510x2.1313=2.8588º,\text{ (93b)}$$

ensuring a drag reduction due to control surfaces. To confirm this, the drag coefficients are calculated from Table 4 for the AOA (93a), and listed in Table 8 for the deflections δ = ± 3°. Interpolating for the deflection δ_B+ in (93b), leads to the drag coefficients:

$$C_{DIX1}=C_{D1}\left(2.8588º\right)=0.00723,\text{ (94a)}$$

$$C_{DIX2}=C_{D2}\left(2.8588º\right)=0.00816,\text{ (94b)}$$

$$C_{DIX3}=C_{D3}\left(2.8588º\right)=0.00782,\text{ (94c)}$$

$$C_{DIX4}=C_{D4}\left(2.8588º\right)=0.00794,\text{ (94d)}$$

$$C_{DIX5}=C_{D5}\left(0.0º\right)=0.008685;\text{ (94e)}$$

using (43a) and Table 3 leads to the total drag coefficients (95a):

$$C_{DIX}=0.00787,\Delta C_{DIX}=C_{DIX}-C_D=0.00218,\Delta C_{DIX}/C_D=0.383,\text{ (95a,b,c)}$$

corresponding to a drag increase of 218 counts (95b) or 38.3% in (95c).Comparison of strategy IX, with strategy VIII in the Table 10 or (90a,b,c) shows that the increase in drag due to a larger AOA, outweighed the drag decrease due to favourable deflection of control surfaces for pitch trim.

Selection of the most effective control surfaces

As a final strategy X, may be considered a further elaboration of strategies VIII-IX, as follows: (i) Of all control surfaces with negative drag slope C'_Di < 0, which should have positive deflection for drag reduction, choose that with larger |C_Di| = -C'_Di drag benefit, or stronger pitching moment slope C'_Mi > 0, or better combination of both specified by larger product-C'_Di C'_Mi; (ii) Of all control surfaces with positive drag slope C'_Di > 0, which should have negative deflection for reduced drag, choose that with largest drag slope coefficient C'_Di, or largest pitching moment coefficient C'_Mi or largest product of the two C'_Di C'_Mi > 0. From Table 11 it follows that only the aileron is in class (iii) Of positive slope of the drag coefficient; the remaining four surfaces have negative drag slope, with the centerbody elevator having the second largest |C'_D0|, and largest C'_Mi and largest product |C'_Di| C_Mi. Thus:

${\delta }_{VII1}\equiv {\delta }^{+}>0={\delta }_{VIII2}={\delta }_{VIII3}={\delta }_{VIII4}>0={\delta }_{VIII5}\equiv {\delta }^{-};\text{ (96)}$

the centerbody elevator is given positive deflection, the aileron is given negative deflection, and all other surfaces are not deflected.

Using (81a, 47a) the condition of cruise lift equilibrium (46) for (96) is:

$0.06177=0.086043{\alpha }_{VIII}-0.011505{\delta }^{+}-0.0049805{\delta }^{-};\text{ (97a)}$

the corresponding condition of pitch trim, viz. C_M = 0 in (49) is:

$0.00819=0.02259{\alpha }_{VIII}+0.00546{\delta }^{+}+0.003297{\delta }^{-}.\text{ (97b)}$

Retaining the untrimmed value of AOA (21a) leads to:

$$0.011505{\delta }^{+}+0.0049865{\delta }^{-}=0,\text{ (98a)}$$

$$0.011546{\delta }^{+}+0.003297{\delta }^{-}=-\mathrm{0.00803.}\text{ (98b)}$$

Solving this leads to the deflections

$$-8.6295º={\delta }^{-}<0<{\delta }^{+}=3.7402º.\text{ (99a,b)}$$

In the case of strategy X, keeping the untrimmed AOA, gives the favourable deflections to reduce drag due to control surface deflection. Together with the low drag for small AOA, this looks promising for low cruise drag. To confirm this the drag coefficients are calculated from Table 5 for the deflections (96) and (99a,b), viz.:

$$C_{DX1}=C_{D1}\left(3.7402º\right)=0.00483,\text{ (100a)}$$

$$i=2,3,4:C_{DXi}=C_{Di}\left(0.0º\right)=0.00569,(100b)$$

$$C_{DX5}=C_{D5}\left(-8.6295º\right)=0.00478+0.00008\times {8.6295}^2=0.00597;\text{ (100c)}$$

using (43a) and Table 3 the corresponding total drag is (101a):

$$C_{DX}=0.00554,\Delta C_{DX}=C_{DX}-C_D=-0.00015,\Delta C_{DX}/C_D=-0.026,\text{ (101a-c)}$$

which represents a drag reduction (101b) of 15 counts or 2.6% in (101c).

Discussion on the Effects of Pitch Trim and Constant Lift in Cruise Drag

The discussion of pitch trim in cruise starts from the remark that it is compatible with (10.1) drag reduction relative to the untrimmed condition. The favourable combination of pitch trim and drag reduction has been found both for optimal and non-optimal pitch trim strategies, both in cases of constant and non-constant lift (10.2).

Combining pitch trim with drag reduction

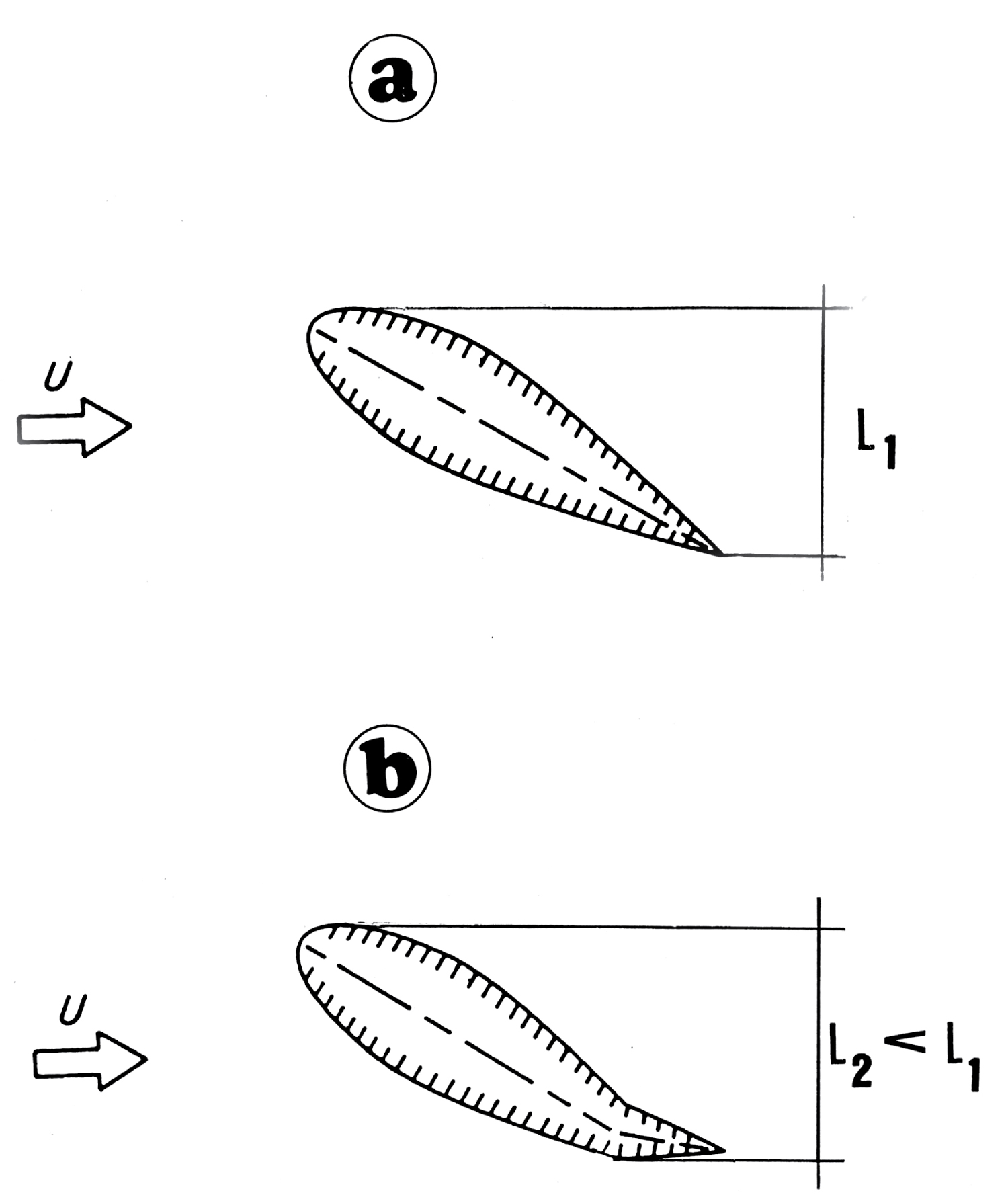
It should not be too surprising that pitch trim can, in the right circumstances, reduce cruise drag. This is illustrated in Figure 1a, which shows at the top a wing profile at AOA, with a stable pitch down moment. The projection perpendicular to the airflow $L_1$ is roughly proportional to drag. In order to trim the 'flying wing' a pitch up moment is produced, by deflecting the elevator up in Figure 1b. This reduces the projection orthogonal to the free stream $L_2<L_1$, leading to lower drag. This simple diagram suggests pitch trim can lead to a cruise drag reduction, for moderate upward deflection of trailing-edge control surfaces. The reality may be less simple than the illustration in Figure 1, and actually relates to the slopes of aerodynamic derivatives for control surfaces in Table 10. It is seen that the derivative of the drag coefficient with regard to control surface deflection is negative in all cases, except for the aileron when it is positive. Thus, the situation in Figure 1 of upward deflection leads to drag reduction for all control surfaces except the aileron. This difference may be due to wing twist or downwash variation along the wing span. In contrast, the derivative of the pitching moment is positive for all control surfaces. The preceding results show that moderate control surface deflections are enough to trim the aircraft if the untrimmed AOA is moderate. Thus, the trim strategy is to achieve lift balance at the smallest possible AOA, so that the nose down pitching moment is moderate, and can be countered by moderate upward deflection of trailing-edge control surfaces.

The possibility of cruise drag reduction by pitch trim was already evident in strategy II of elevator deflection upwards. Since this reduces lift, the trim AOA has to be increased relative to the untrimmed value, as shown is Table 9. The optimisation strategy V with strategy II as initial condition ultimately suggests strategy X which achieves the lowest cruise drag with pitch trim in Table 10. The intermediate step was as shown in the strategy IX of minimization drag by deflecting upward by the same amount (i) All control surfaces with negative drag derivative and deflecting downward by the same amount (ii) All surfaces with positive drag derivative. The two collective deflections can be chosen to satisfy lift equilibrium and pitch trim. The strategy X is derived from strategies VIII-IX by choosing in each group (i) and (ii) the most effective control surface in terms of (a) Drag reduction, (b) Pitch trim or (a) combination of both. The ten strategies I to X are summarized in List 1; the two strategies which combine pitch trim and lift balance with the largest drag reduction are singled-out in Table 12.

The Table 13 ranks the strategies according to the most desirable features, viz.: (i) Lowest cruise drag; (ii) Smallest AOA; (iii) Smallest control deflections in the sense of smallest average of modulus of largest and smallest deflection $\overline{\delta }\equiv \left(\left|{\delta }_{\min }\right|+\left|{\delta }_{\max }\right|\right)/2;$ (iv) Linear aerodynamics works best for smallest AOA α and smallest mean deflection $\overline{\delta }$; (v) Simplicity of the computational algorithm, viz. least number of variables and least iterations. The strategy X has been shown to have five relative advantages: (i) It has the second lowest trimmed cruise drag of all eight strategies and twelve sub-strategies considered: (ii) The trimmed AOA is unchanged from the untrimmed value, and hence is the lowest and small; (iii) The pitching moment is thus small, and leads to moderate (5^th smallest) control surface deflections; (iv) The small AOA and control surface deflections imply that linear aerodynamics can give reliable results (3^rd best); (v) The strategy is easy to apply (3^rd best). The other pitch trim strategies considered in Table 13 do not have one or more of these attributes.

Comparative effectiveness of eight pitch trim strategies

The reasons why strategy X is quite effective may be explained as follows: (i) The ailerons are the only control surfaces for which a positive deflection reduces drag; (ii) For the remaining control surfaces, a negative deflection reduces drag; (iii) Of the latter, the centerbody elevator provides the best combination of large pitching moment for trim and relatively large drag reduction; (iv) Positive deflection of the elevator and negative deflection of the aileron can balance each other for the effect on lift; (v) Thus the untrimmed AOA is unchanged by pitch trim, and there is no drag penalty; (vi) The unchanged drag due to AOA, and reduced drag to control surface deflection, yield a cruise drag reduction due to trim; (vii) The small AOA and moderate control surface deflections give confidence on the predictions of linear aerodynamics; (viii) This pitch trim strategy is simple to apply, since it involves only two control surface deflections, and no change in AOA.

The strategy II of deflection of centerbody elevator alone gave a slightly better cruise drag reduction due to trim (minus 18 drag counts) than the strategy X of opposite deflection of the aileron also (minus 15 drag counts). However, strategy X allows an unchanged, hence small AOA of 0.7° whereas strategy II increases AOA by a factor of three to 2.1°. For this reason, strategy X is considered preferable. It is also possible to explain why other strategies are less successful or even unfavourable. For example, the strategy I of equal deflection of all control surfaces, does not exploit the drag reduction due to the deflection of the ailerons opposite to the other control surfaces; thus it leads to high cruise drag due to trim. The same applies to strategy III, of preferential deflection of inner control surfaces, which do not use aileron deflection to reduce cruise drag and AOA. The methods which give intermediate results, like the early iterations, not fully converged, of the optimal strategies V, exhibit deflection of outer control surfaces opposite to inner control surfaces, but do not exploit them fully. It is clear from the present account that the choice of the best pitch trim strategy is guided by the aerodynamic derivatives of the particular aircraft configuration and the control surfaces available for pitch trim.

The preceding are examples of the qualitative explanation of the results obtained in Table 13 for each of the eight pitch trim strategies in List 1, viz.: (i) The strategy I of equal deflection of all control surfaces, causes the ailerons to be deflected as the inner control surfaces, thus increasing drag and trimmed AOA; (ii) The strategy II of deflection of centerbody elevator alone, is effective at reducing cruise drag, but also reduces lift, and requires increased AOA for trim, with no AOA reduction provided by the undeflected aileron; (iii) The strategy III of preferential deflection of inner control surfaces, also does not deflect the ailerons, and thus leads to an increased AOA for trim, which dominates cruise drag; (iv) The optimal strategies IV and V evolve from any initial condition in the right direction, deflecting in opposition inner and outer control surfaces, but the convergence is slow, and a few iterations do not reach the best results; (v) The strategy VI of equal contribution to lift from all control surfaces, does not use the ailerons to reduce lift and trimmed AOA, and hence also increases cruise drag; (vi) The sub-optimal strategy VII of multiplying the optimal deflection by a constant, determined from cruise lift equilibrium, improves on strategy for the same number of iterations, because it accelerates convergence; (vii) The strategies VIII-IX of deflecting the ailerons opposite to all other inner control surfaces is correct, but is spoiled by poor lift balance of the single aileron versus all the other inner control surfaces leading to a large trimmed AOA and hence increase in cruise drag; (viii) The strategy X works out best because it deflects the ailerons in opposition to centerbody elevator alone, achieving lift equilibrium with unchanged small AOA, and requiring moderate control surface deflections each of which contributes to cruise drag reduction. Thus a discerning use of simple pitch trim strategies turns out to be more effective than brute force recourse to computationally complex and slow converging optimal procedures.

Conclusion

In a conventional aircraft configuration the elevator or all-flying tail is the only effective pitch control surface. The elevator must be large enough to provide adequate pitch control authority at low speed, when large deflections are possible. At high speed, when aerodynamic and/or aeroelastic effects may limit deflections, the higher dynamic pressure may compensate, and not be a “sizing” criterion requiring large area, with aerodynamic, aeroelastic, weight or actuator problems. In any case the compromise in elevator sizing is straightforward once the required pitching moment and possible lever arm are known. The BWB or FW configuration has the potential to provide pitch trim with several combinations of control surface deflections. There are simple choices with obvious consequences but it is not clear what is the best compromise, e.g.: (i) The strategy II of deflecting the centerbody elevator only can lead to a large deflection; (ii) Using all control surfaces with the same deflection (strategy I) or same lift (strategy VI) does not exploit the most effective controls; (iii) Deflecting preferentially the inner control surfaces with an aeroelastic limit (strategy III) may not be the best compromise among the preceding choices.

The optimization methods may or may not do better than the simpler non-optimal strategies depending on whether the drag has a single global minimum or several local minima. If there are several local minima convergence will occur to that closest to the initial condition. The influence of the initial condition on the result of the optimization may not be obvious. It may be difficult to know if a local minimum is lower that neighbouring ones or is the global minimum. Also the optimization algorithm may require data, like second-order control derivatives which is not accurate, leading to a possible dilemma: (i) Too few iterations do not converge closely enough to the optimum; (ii) Too many iterations accumulate too large an error around the optimum. It may also occur that the local minimum is outside the acceptable range of control deflections, and the optimum is not a local minimum but rather the best value on a boundary. Thus, optimal methods have strengths and weakness which may be different from simple methods and a combination of the two may be more effective than either of them.

A careful examination of control derivatives is essential to understand how an optimization procedure is going to work, or what are the consequences of a simple strategy. In the case of pitch trim for cruise the starting ideas seems to be to select the most effective control surfaces, in the sense of combining the largest possible pitching moment and drag reduction with small deflections; it is also important to achieve lift balance, so that it is not necessary to increase the AOA for trimming purposes. A larger AOA increases drag, may require a larger pitching moment, and thus works against having selected trim with the “most effective” control surfaces; thus the most effective control surfaces should be chosen to (i) Provide pitching moment, (ii) Reduce drag and (iii) Balance lift. In the present example it was possible to achieve pitch trim while reducing drag relative to an untrimmed flight condition, also not changing AOA; the latter contributes to smaller control deflections, avoiding undesirable aeroelastic effects, and staying within the limits of linear or weakly non-linear aerodynamics and control methods.

Acknowledgements

This work was supported by FCT (Foundation for Science and Technology), through IDMEC (Institute of Mechanical Engineering), under LAETA, project UID/EMS/50022/2019. This work was started under the NACRE project of the European Union and benefited from comments of other partners in this activity.

References

1. Dollyhigh S (1970) Some trim drag considerations for maneuvering aircraft. AIAA 2^nd Aircraft Design and Operations Meeting.
2. Goldstein S, Combs C (1974) Trimmed drag and maximum flight efficiency of aft tail and canard configurations. AIAA 12^th Aerospace Sciences Meeting.
3. McLaughlin M (1977) Calculations, and comparison with an ideal minimum, of trimmed drag for conventional and canard configurations having various levels of static stability. NASA Technical Note, 1-22.
4. Kendall E (1984) The minimum induced drag, longitudinal trim and static longitudinal stability of two-surface and three-surface airplanes. AIAA 2^nd Applied Aerodynamics Conference.
5. Ende R (1989) The effects of aft-loaded airfoils on aircraft trim drag. AIAA 27^th Aerospace Sciences Meeting.
6. Campos LMBC, Marques JMG (2015) On the minimization of cruise drag due to pitch trim for a flying wing configuration. The CEAS Air and Space Conference, Delft University of Technology, The Netherlands.
7. Rahman NU, Whidborne JF (2010) Propulsion and flight controls integration for a blended-wing-body transport aircraft. J Aircraft 47: 895-903.
8. Haiqiang D, Xiongqing Y, Hailian Y, et al. (2015) Trim drag prediction for blendedwing-body UAV configuration. Trans Nanjing Univ Aeronaut Astronaut 32: 133-136.
9. Griffin BJ, Brown NA, Yoo SY (2011) Intelligent control for drag reduction on the X-48B vehicle. AIAA Guidance, Navigation and Control Conference, Portland, Oregon.
10. Durham W (1993) Constrained control allocation. J Guid Control Dyn 16: 717-725.
11. Harkegard O (2004) Dynamic control allocation using constrained quadratic programming. J Guid Control Dyn 27: 1028-1034.
12. Bolender MA, Doman DB (2005) Nonlinear control allocation using piecewise linear functions: A linear programming approach. J Guid Control Dyn 28: 558-562.
13. Bodson M (2011) Evaluation of optimization methods for control allocation. J Guid Control Dyn 34: 380-387.
14. Cook MV, de Castro HV (2004) The longitudinal flying qualities of a blended-wingbody civil transport aircraft. Aeronaut J 108: 75-84.
15. Roysdon PF, Khalid M (2011) Blended-wing-body lateral-directional stability investigation using 6DOF simulation. AIAA Infotech at Aerospace Conference and Exhibit, St. Louis, Missouri.
16. Peterson T, Grant PR (2011) Handling qualities of a blended wing body aircraft. AIAA Atmospheric Flight Mechanics Conference, Portland, Oregon.
17. Jung DW, Lowenberg MH (2005) Stability and control assessment of a blendedwing-body airliner configuration. AIAA Atmospheric Flight Mechanics Conference and Exhibit, San Francisco, California.
18. Cameron D, Princen N (2000) Control allocation challenges and requirements for the blended wing body. AIAA Guidance, Navigation and Control Conference and Exhibit.
19. Wildschek A, Stroscher F, Klimmek T, et al. (2010) Gust load alleviation on a large blended wing body airliner. 27^th International Congress of the Aeronautical Sciences, Nice, France.
20. Waters SM, Voskuij M, Veldhuis LLM, et al. (2013) Control allocation performance for blended wing body aircraft and its impact on control surface design. Aerospace Science and Technology 29: 18-27.
21. Wildschek A, Bartosiewicz Z, Mozyrska D (2014) A multi-input multi-output adaptive feed-forward controller for vibration alleviation on a large blended wing body airliner. J Sound Vib 333: 3859-3880.
22. Kozek M, Schirrer A (2015) Modeling and control for a blended wing body aircraft - a case study. Advances in Industrial Control, Springer.
23. Peifeng L, Binqian Z, Yingchun C, et al. (2012) Aerodynamic design methodology for a blended wing body transport. Chinese Journal of Aeronautics 25: 508-516.
24. Campos L (2015) On physical aeroacoustics with some implications for low-noise aircraft design and airport operations. Aerospace 2: 17-90.
25. Huijts C, Voskuij M (2015) The impact of control allocation on trim drag of blended wing body aircraft. Aerospace Science and Technology 46: 72-81.
26. Okonkwo P, Smith H (2016) Review of evolving trends in blended wing body aircraft design. Progress in Aerospace Sciences 82: 1-23.
27. Bisplinghoff RL, Ashley H, Halfman RL (1955) Aeroelasticity. Addison-Wesley.
28. Holt RJ, Ashley H (1962) Aeroelasticity. Wiley.
29. Försching H (1974) Aeroelastizitat. Springer Verlag.
30. Dowell EH (1975) Aeroelasticity of plates and shells. Noordhoff International Publishing, Leyden.
31. Dowell EH (2004) A modern course of aeroelasticity. Kluwer.
32. Lamb H (1932) Hydrodynamics. (6th edn), Cambridge University Press.
33. Batchelor GK (1967) An introduction to fluid dynamics. Cambridge University Press, Cambridge.
34. Prandtl L, Tietjens OG (1934) Fundamentals of hydro and aeromechanics. Teubner.
35. Duncan WJ, Thom AS, Young AD (1960) The mechanics of fluids. Arnold.
36. Lighthill MJ (1986) An informal introduction to theoretical fluid mechanics, Clarendon Press.
37. van Dyke M (1985) Perturbation methods in fluid dynamics. Parabolic Press.
38. Glauert H (1936) The elements of airfoil and airscrew theory. Cambridge University Press.
39. Abbott IH, Doenhoff AE (1949) Theory of wing sections. Mc-Graw Hill.
40. Durand WF (1963) Aerodynamic theory. Springer, Berlin.
41. Milne-Thomson LM (1958) Theoretical aerodynamics. MacMillan.
42. von Mises R, Friederichs KO (1971) Fluid dynamics. Springer.
43. Kuethe AM, Chow CY (1986) Foundations of aerodynamics: Bases of aerodynamic design, 4th ed. Wiley.
44. Anderson JD (2001) Fundamentals of aerodynamics. (3rd edn), McGraw-Hill.
45. Thwaites BW (1960) Incompressible aerodynamics. Claredon Press.
46. Karamcheti K (1966) Principles of ideal-fluid aerodynamics. Wiley.
47. Courant R, Friedrichs KO (1976) Supersonic flow and shock waves. Springer.
48. von Mises R (1958) Compressible fluid flow. Academic Press.
49. Ockendon H, Ockendon JR (2004) Waves and compressible flow. Springer.
50. Birkhoff G, Zarantonello EH (1957) Jets, wakes and cavities. Academic Press.
51. Schlichting H, Gersten K (1997) Grenzschicht-theorie: Springer.
52. Saffman PG (1992) Vortex dynamics. Cambridge University Press.
53. Drazin PG, Reid WH (1981) Hydrodynamic stability. Cambridge University Press.
54. Hinze JO (1975) Turbulence. Mcgraw-Hill, New York.
55. Campos LMBC (2011) Complex analysis with applications to flows and fields. CRC Press.
56. Campos LMBC (2012) Transcendental representations with applications to solids and fluids. CRC Press.
57. Campos LMBC (2014) Generalized calculus with applications to matter and forces. CRC Press.
58. McRuer D, Graham D, Ashkenas I (1973) Aircraft dynamics and automatic control. Princeton University Press.
59. Etkin B (1982) Dynamics of flight - stability and control. Wiley.
60. Nelson RC (1998) Flight stability and automatic control. (2^nd edn), McGraw-Hill, New York.
61. Stevens BL, Lewis FL (1992) Aircraft control and simulation. Wiley.
62. Tischler MB (1994) Aircraft flight control. International Journal of Control.
63. Roskan J (2001) Airplanes flight dynamics and automatic flight controls. (3^rd edn), DAR Corporation.
64. Tischler MB (1996) Advances in aircraft flight control. Taylor & Francis.
65. Blakelock JH (1991) Automatic control of aircraft and missiles. 2^nd Ed. Wiley.
66. Wood RM (2003) Aerodynamic drag and drag reduction: energy and energy savings. 41st AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV.
67. Reneaux J (2004) Overview on drag reduction technologies for civil transport aircraft. European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS), Jyvaskyla, Sweden.
68. Campos LMBC, Marques JMG On a method of Lagrange multipliers for cruise drag minimization (in preparation).
69. LMBC Campos, JMG Marques (2019) On the maximisation of control power in low-speed flight. The Aeronautical Journal 213: 1099-1121.