A Modified Particle Filter for SINS/SAR Integrated Navigation

Abstract

This paper presents a modified particle filter for SINS/SAR (Strap-down Inertial Navigation System/Synthetic Aperture Radar) integrated navigation. This method is developed by adopting Markov Chain Monte Carlo (MCMC) moves to the particle regularization process. It combines local resampling with MCMC moves to prevent particle degeneracy and also guarantee that the resultant particles are in the same distribution as probability distribution function, without causing extra noise on state estimate. Simulation results demonstrate that the proposed method can effectively prevent the problem of particle degeneracy, and its filtering accuracy for SINS/SAR integrated navigation is much higher than that of the classical particle filter and regularized particle filter.

Keywords

Strap-down inertial navigation, Synthetic aperture radar, Integrated navigation, Particle filter, Regularization, Markov chain monte carlo

Introduction

SINS/SAR (Strap-down Inertial Navigation System/Synthetic Aperture Radar) integrated navigation aims to obtain high-precision position and azimuth by using correlated images [1,2]. The high-precision information of SINS can be used for motion compensation and precise calibration of antennae to correct the error of SAR. In reverse, under the support of digital map databases, SAR can also correct the error of SINS, which is increased with time, according to the target information [3]. Due to the complementary nature of SINS and SAR, SINS/SAR integrated navigation represents a promising solution for achieving high-precision positioning navigation.

The precision of SINS/SAR integrated navigation depends on the performance of the filtering algorithm. Currently, the extended Kalman filter is a commonly used method for nonlinear systems [4,5]. This is an approximation method, in which nonlinear system equations are linearized by the Taylor expansion and the linearized states are assumed to obey the Gaussian distribution. The linearization stage of the state equations may lead to the biased or even divergent filtering solution [6].

The particle filter (PF) is an optimal recursive Bayesian filtering method based on Monte Carlo simulation [7,8]. It can produce a sample of independent random variables with distribution subject to the conditional probability distribution. Since this method is not limited by linearization error and the assumption of Gaussian noise, it can be used to deal with nonlinear system models and non-Gaussian noise. It is also easier to implement, even for high-dimensional problems. Therefore, the PF has been widely used in the fields of navigation, target tracking, fault detection, robotic control and computer vision [9,10]. However, with the PF, the particle degeneracy phenomenon may occur frequently in the approximation process. The approximation process may also diverge if a dynamic system has a very small noise or the measurement noise has a very small variance [7-10].

Research efforts have focused on studying the problem of particle degeneracy in the PF [11-13]. Resampling is the earliest method to deal with the problem of particle degeneracy [11]. The importance sampling improves the resampling method by adopting an important density function to the resampling process [12]. However, the re-sampling and important sampling methods result in the loss of diversity among particles since particles are drawn from a discrete distribution, rather than a continuous distribution. They also cause the exhaustion of particles and a large computational load. The regularized PF improves the resampling and importance sampling methods by resampling the particle set from a continuous approximation of the probability density function [13]. However, the resultant particles do not share a common distribution with the actual probability function, and the variance of state estimation is also increased. Markov Chain Monte Carlo (MCMC) is a technique to increase the diversity of particles by moving particles to new points in the state space [14,15]. It enables particles to be distributed according to the desired distribution. The design of a Markov transition kernel can also be applied to each particle to prevent a large number of posteriorly selected particles from being rejected. Therefore, it is necessary to introduce the MCMC technique to the particle regularization process to overcome the problem of particle degeneracy and improve the particle distribution.

Currently, most of the existing filtering methods for integrated navigation are mainly dominated by the optimal Kalman filter [16,17]. The application of a PF in integrated navigation, especially in SINS/SAR integrated navigation, is still in infancy. In SINS/SAR integrated navigation, SINS has small process noise which is exponentially unstable. The error caused by system model uncertainty is accumulated in the navigation process, decreasing the accuracy of the navigation solution. If directly using the PF in SINS/SAR integrated navigation, it may not only cause the phenomenon of particle degeneracy, but it may also keep particles far away from the desired sampling area in the state space [18].

This paper presents a modified PF for SINS/SAR integrated navigation by using the MCMC technique. This filter is developed by incorporating MCMC moves into the regularization process. It combines local resampling with MCMC moves to prevent the degeneracy of particles and ensure that the resultant particles have a common distribution with the actual probability function, without causing noise on state estimate. Simulations and comparison analysis have been conducted to comprehensively evaluate the performance of the proposed filtering method for SINS/SAR integrated navigation.

Mathematical Model of SINS/SAR Integrated Navigation

System state equation

The system state vector x(t) of SINS/SAR integrated system is defined as

$$x(t)={[q_0,q_1,q_2,q_3,\delta v_E,\delta v_N,\delta v_U,\delta L,\delta \lambda ,\delta h,{\epsilon }_{bx},{\epsilon }_{by},{\epsilon }_{bz},{\nabla }_{bx},{\nabla }_{by},{\nabla }_{bz}]}^T\text{ (1)}$$

where (q₀, q₁, q₂, q₃) is the attitude error quaternion, (δv_E, δv_N, δv_U) the velocity error, (δL, δλ, δh) the position error, (ε_bx, ε_by, ε_bz) the gyro constant drift, and $({\nabla }_{bx},{\nabla }_{by},{\nabla }_{bz})$ the accelerometer zero bias.

The system state equation is described as

$$\dot{x}(t)=f(x(t))+G(t)w(t)\text{ (2)}$$

where f(.) and G(t) are the nonlinear function and noise coefficient matrix [19], and w(t) is the process noise described by

$$w(t)={[w_{gx},w_{gy},w_{gz},w_{ax},w_{ay},w_{az}]}^T\text{ (3)}$$

where (w_gx, w_gy, w_gz) is the gyro white noise and (w_ax, w_ay, w_az) is the accelerometer white noise.

Measurement equation

Both SINS and SAR can output the position information (latitude, longitude, and altitude for SINS and latitude and longitude for SAR) and heading angle to position a dynamic vehicle. A barometric altimeter is introduced to the SINS/SAR integrated navigation to stabilize the altitude of SINS. Based on above, the measurement vector is chosen as

$$y_k={\left[\begin{array}{cccc}{\varphi }_I-{\varphi }_S& L_I-L_S& {\lambda }_I-{\lambda }_S& h_I-h_B\end{array}\right]}^{\text{T}}={\left[\delta \varphi ,\delta L,\delta \lambda ,\delta h\right]}^{\text{T}}\text{ (4)}$$

where (ϕ_I, L_I, λ_I, h_I) is the heading angle, latitude, longitude and altitude of SINS, (ϕ_S, L_S, λ_S) is the heading angle, latitude and longitude of SAR, and h_B is the altitude output of the barometric altimeter.

The measurement equation is given as

$$y_k=h(x_k)+v_k\text{ (5)}$$

where h(.) is the nonlinear function describing the measurement model [19], and v_k represents the measurement noises of the SAR and barometric altimeter.

Classical Particle Filter

The classical PF [7,8] describes a probability distribution by using random samples. Based on noisy measurement data, it approximates the actual probability distribution by adjusting the weights of particles and the positions of samples to estimate the system states in the sense of minimum variance. The key of particle filtering is that the posterior probability distribution of a dynamic system state, i.e. p(x_0:k|y_1:k), is calculated by Monte Carlo approximation under noisy measurements. Based on importance sampling and resampling steps, the objective is to generate an independent sample set which has the same distribution as the actual probability function. Since it is difficult to draw particles directly from the actual probability distribution, particles are drawn sequentially from a proposed distribution q(x_0:k|y_1:k). Denote $x_k^{\left(i\right)}~q\left(x_k|x_{0:k-1}^{\left(i\right)},y_{1:k}\right)$, using a random weighting sample ${\left\{x_k^{(i)},w_k^{(i)}\right\}}_1^N$ the posterior probability density function can be represented as

$$p\left(x_{0:k}|y_{1:k}\right)\cong {\displaystyle \sum _{i=1}^N{w}_k^{\left(i\right)}}\delta \left(x_{0:k}-x_{0:k}^{\left(i\right)}\right)\text{ (6)}$$

where weight $w_k^{(i)}$ satisfies the normalized condition ${\displaystyle \sum _{i=1}^N{w}_k^{\left(i\right)}}=1$

Modified Particle Filter

The PF approximates the posterior distribution function at each time point k by using a particle set ${\left\{x_k^{\left(i\right)}\right\}}_1^N$. However, the particle degeneracy phenomenon may occur frequently in the approximation process described by (6), as the number of useful particles is significantly reduced after a few iterations. This paper adopts MCMC moves to the regularization process of particles to overcome this problem. A modified PF is developed by combining local resampling with MCMC moves to prevent the depletion of particles and enable the resultant particles to have the same distribution as the actual probability function.

Regularization

The purpose of this step is to generate a new particle set ${\left\{x_k^{{}^{\ast }\left(i\right)}\right\}}_1^N$ by applying a regularization kernel to original particle set ${\left\{x_k^{\left(i\right)}\right\}}_1^N$. In order to do so, the set of particles is resampled according to a continuous approximation of actual probability density function ${\widehat{p}}_c$ instead of (6) in the classical PF

$${\widehat{p}}_c\left(x_k^{}|y_{1:k}\right)={\displaystyle \sum _{i=1}^N{w}_k^{\left(i\right)}}{K}_h\left(x_k^{}-x_k^{\left(i\right)}\right)\text{ (7)}$$

where K_h is the scaled kernel described by

$$K_h=\frac{{\left(\det S\right)}^{{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{n_x}{{}^{}}^{}}}{h}K\left(\frac{1}{h}{A}^{-1}x\right)\text{ (8)}$$

where h is the bandwidth, $n_x$ is the size of the state vector, and S = AA^T is the covariance matrix. K is the kernel density, which is symmetric and satisfies ${\displaystyle \int K(x)}dx=1$ and ${{\displaystyle \int \Vert x\Vert }}^{2}K(x)dx<\infty$.

If the probability density is a single-peaked curve, the derived optimal bandwidth is

$$h_{opt}={\left(4/\left(n_x-2\right)\right)}^{\frac{1}{n_x+4}}{N}^{-\frac{1}{n_x+4}}\text{ (9)}$$

The case of multimodal density models can be handled by choosing h = h_opt∕2.

Metropolis-Hastings (M-H) rules

The regularization technique, which is used in the regularized PF, is to replace the discrete approximation by a continuous approximation in a window to increase the diversity of particles [13]. However, the particles are no longer distributed according to the target distribution but the non-parametric approximation, leading to the increase in the variance of state estimate. The proposed method addresses this problem by combining MCMC moves into the particle regularization process. It develops the Metropolis-Hastings rules to accept/reject the particles updated by the regularization process, ensuring that selected particles are distributed according to the target distribution.

In this step, a new particle trajectory ${\left\{x_{0:k}^{{}^{\ast }\left(i\right)}\right\}}_1^N$ is generated by extracting L-1 particles (L is a positive integer) from the original particle set ${\left\{x_k^{\left(i\right)}\right\}}_1^N$, leaving the remaining particles unchanged. The new particle trajectory is accepted or rejected according to the M-H rules.

For the sake of conciseness, the particles in the original particle set $x_{k-1}^{(i)}$ are called the parent particles, while the particles in the new particle set $x_k^{{}^{\ast }(i)}$ are called the child particles. Due to the small noise process of SINS, the parent particles may be discarded, thus leading to the rejection of trajectory $\left(x_k^{{}^{\ast }(i)},x_{0:k-1}^{(i)}\right)$ by the M-H rules. To overcome this problem, a local resampling step is utilized to generate a new trajectory. The new trajectory $x_{0:k}^{{}^{\ast }(i)}$ is generated by updating L-1 particles $x_{k-L:k-1}^{(i)}$ through resampling. Since only L-1 particles are resampled, the MCMC moves do not cause any extra computational load. The new trajectory consists of three components.

$$x_{0:k}^{{}^{\ast }(i)}=\left(x_k^{{}^{\ast }(i)},x_{k-L:k-1}^{{}^{\ast }(i)},x_{0:k-L-1}^{(i)}{}_{}\right)\text{ (10)}$$

where $x_k^{{}^{\ast }(i)}$ is generated by a kernel approximation, $x_{k-L:k-1}^{{}^{\ast }(i)}~p\left(x_{k-L:k-1}^{}|x_k^{{}^{\ast }(i)},x_{0:k-L-1}^{(i)},y_{1:k-1}\right)$, and $x_{0:k-l-1}^{(i)}$ is a portion of the original trajectory.

The local sampling step enables the new particle trajectory to sufficiently approximate the actual distribution, thus increasing the acceptance rate of the M-H rules. According to the M-H rules, the acceptance probability of the i^th trajectory is

$$\phi \left({x^{\prime }}_{0:k}^{(i)}|x_{0:k}^{(i)}\right)=\min \left\{1,\beta \left({x^{\prime }}_{0:k}^{(i)}|x_{0:k}^{(i)}\right)\right\}\text{ (11)}$$

where β is the acceptance rate, which is represented as

$$\beta \left({x^{\prime }}_{0:k}^{(i)}|x_{0:k}^{(i)}\right)=\frac{p\left({x^{\prime }}_{0:k}^{(i)}|y_{1:k}^{}\right)q\left(x_{0:k}^{(i)}|{x^{\prime }}_{0:k}^{(i)}\right)}{p\left(x_{0:k}^{(i)}|y_{1:k}\right)q\left({x^{\prime }}_{0:k}^{(i)}|x_{0:k}^{(i)}\right)}\text{ (12)}$$

where q is the proposed distribution.

As the candidate trajectories are coincident with each other from time 0 to time k- -1, the following result can be obtained

$$\frac{p\left({x^{\prime }}_{0:k}^{(i)}|y_{1:k}^{}\right)}{p\left(x_{0:k}^{(i)}|y_{1:k}^{}\right)}=\frac{{\displaystyle \prod _{t=k-L}^{k}p(y_t|{x^{\prime }}_{0:t}^{(i)},y_{0:t-1})p({x^{\prime }}_t^{(i)}{x^{\prime }}_{0:t-1}^{(i)})}}{{\displaystyle \prod _{k=t-L}^{t}p(y_t|x_{0:t}^{(i)},y_{0:t-1})p(x_t^{(i)}|x_{0:t-1}^{(i)})}}\text{ (13)}$$

The distribution q is the contribution of the regularization and the local resampling process. As the Gaussian regularization Kernel is symmetric, the proposed distribution ratio is reduced to

$$\frac{q\left(x_{0:k}^{(i)}|{x^{\prime }}_{0:k}^{(i)}\right)}{q\left({x^{\prime }}_{0:k}^{(i)}|x_{0:k}^{(i)}\right)}=\frac{p(x_{k-L:k-1}^{(i)}|x_k^{(i)},x_{0:k-L-1}^{(i)},y_{1:k-1})}{p({x^{\prime }}_{k-L:k-1}^{(i)}|{x^{\prime }}_k^{(i)},x_{0:k-L-1}^{(i)},y_{1:k-1})}\text{ (14)}$$

It can be seen from the above analysis that the M-H rules together with local resampling increase the acceptance rate and guarantee the resultant particle trajectory is distributed according to the target distribution, thus overcoming the limitation of the regularized PF.

Performance Evaluation and Discussions

Simulations were conducted to evaluate and analyze the performance of the modified PF for SINS/SAR integrated navigation. The comparison analysis of the modified PF with the classical PF and regularized PF [13] is also discussed in this section.

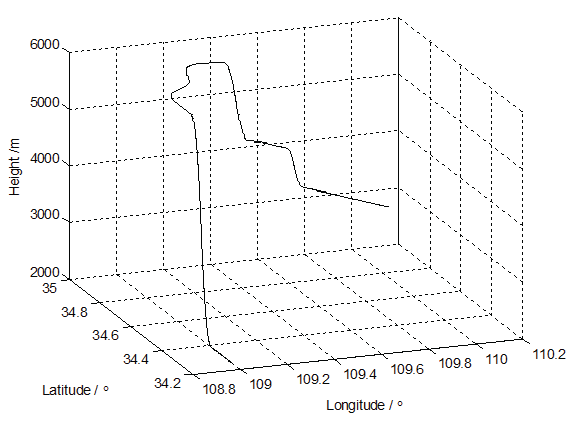
In order to analyze the performance of the proposed method under flexible and high speed flying conditions, the flight trajectory, which involves different flight states such as accelerating, climbing and turning states (Figure 1), was designed according to the actual flight process of an ASN 206 reconnaissance UAV. The navigation frame was chosen as the E-N-U (East-North-Up) geography frame. The aircraft was initially at North latitude 34.2°, East longitude 108.9°, and altitude 2000 m. Its velocity at the initial position was 0 m/s, 100 m/s and 0 m/s in East, North, and Up, respectively. Its initial orientation was assumed to be parallel to the navigation frame. The initial position error was (10 m, 10 m, 15 m), initial velocity error (0.8 m/s, 0.8 m/s, 0.8 m/s) and initial attitude error (1.2', 1.2', 1.5'). The end position of the UAV was at North latitude 34.8°, East longitude 110.6°, and altitude 2748 m. The UAV maximum speed and altitude were 190 km/h and 5875 m. The UAV flight time and distance were 1000 s and 28 km. The detailed simulation parameters are listed in Table 1.

For the purpose of comparison analysis, trials were conducted under the same conditions by the classical PF, regularized PF and proposed modified PF for filtering the navigation data from the SINS, SAR and barometric altimeter. The estimation error was calculated by taking the pre-designed trajectory as reference.

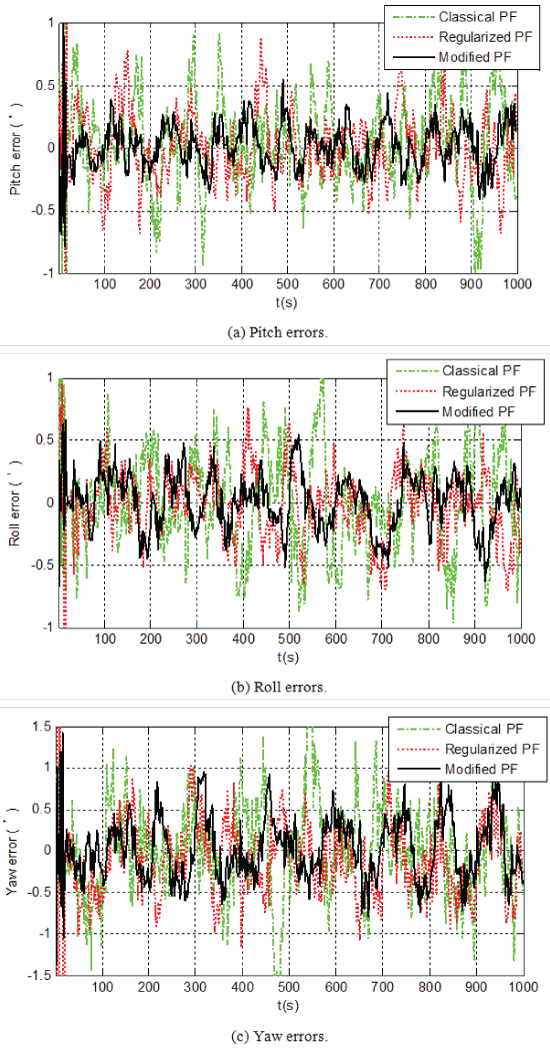
Figure 2 illustrates the attitude errors obtained by these three filtering methods, respectively. It can be seen that during the time period from 100 s to 1000 s, the classical PF results in the largest magnitude of oscillations in the estimation curves of the attitude error. The attitude errors in Pitch, Roll and Yaw are within (- 1.01', 1.26'), (- 0.96', 1.12') and (- 2.09', 1.92'), respectively. The reason is that the degeneracy problem of particles is involved in the classical PF during the filtering process. The regularized PF significantly improves the performance of the classical PF, leading to the attitude error within (- 0.71', 0.86'), (- 0.73', 0.76') and (- 1.17', 1.25') in Pitch, Roll and Yaw, respectively. Compared with the above two methods, the attitude estimation errors of the proposed modified PF are the smallest, which are within (- 0.40', 0.54'), (- 0.58', 0.53') and (- 0.78', 0.93') in Pitch, Roll and Yaw, respectively.

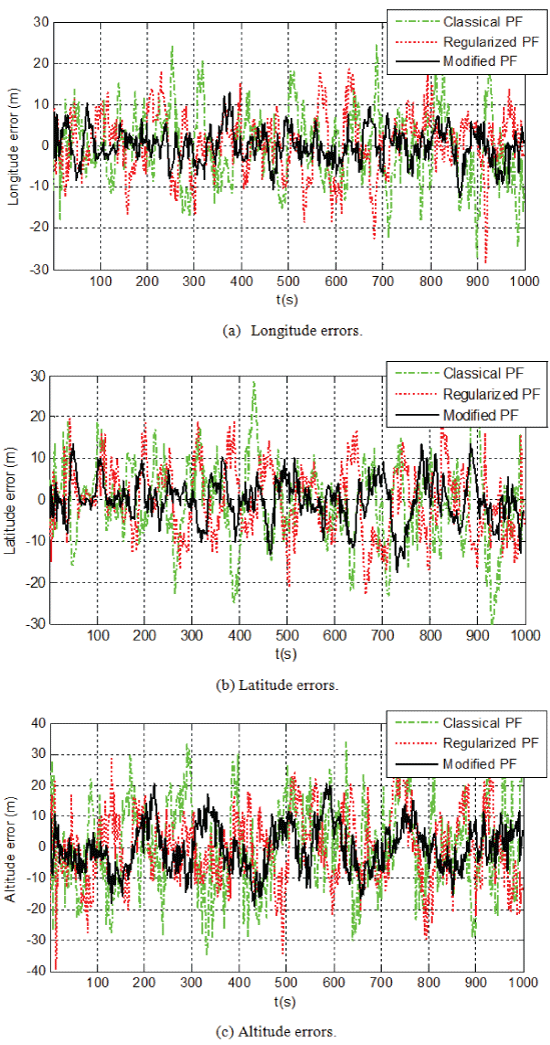
Figure 3 show the position errors obtained by the classical PF, regularized PF and proposed modified PF. It can be seen that the position errors have the similar trend as the attitude errors for these three methods. During the time period from 100 s to 1000 s, the position errors in longitude, latitude and altitude estimated by the classical PF are within (- 26.92 m, 24.42 m), (- 30.08 m, 30.33 m) and (34.74 m, 36.28 m), respectively. The regularized PF decreases the estimation errors of the classical PF, and the resultant position errors in longitude, latitude and altitude are within (- 26.11 m, 18.57 m), (- 21.98 m, 21.51 m) and (- 33.43 m, 32.57 m). In contrast, the position errors in longitude, latitude and altitude by the proposed modified PF are within (- 12.70 m, 12.93 m), (- 17.39 m, 13.51 m) and (- 19.01 m, 20.69 m), which are smaller than those of the classical PF and regularized PF.

The mean absolute errors (MAE) and standard deviations (STD) of the attitude errors and position errors obtained by the classical PF, regularized PF and proposed modified PF in the time period from 100 s to 1000 s are shown in Table 2. It can be seen that the MAE and STD of the modified PF are much smaller than those of the other two filters.

The above simulations and analysis demonstrate the proposed modified PF overcomes the limitation of the classical PF in terms of the degeneracy problem of particles. The achieved navigation accuracy for SINS/SAR integrated navigation is also much higher than that of the classical PF and regularized PF.

Conclusions

This paper presents a modified PF for SINS/SAR integrated navigation. The MCMC technique combined with local resampling is developed and incorporated in the regularization process of particles to prevent particle degeneracy and ensure that the resultant particles have a common distribution with the actual probability function without causing additional noise on state estimate. Simulation results demonstrate that the proposed method overcomes the problem of particle degeneracy in the classical PF, and its accuracy for SINS/SAR integrated navigation is much higher than that of the classical PF and regularized PF.

Future research work will focus on the improvement of the proposed modified PF by using artificial intelligence. Advanced expert systems and neural networks will be established to automatically and adaptively adjust the size of sample sets during the estimation process according to estimation variance.

Acknowledgements

The work of this paper was supported by the National Natural Science Foundation of China (Project Number: 61174193) and the Specialized Research Fund for the Doctoral Program of Higher Education (Project Number: 20136102110036). It was also supported by the Australian Research Council (ARC) Discovery Early Career Award (DECRA) (DE130100274).

References

1. S Gao, Y Zhong, X Zhang, et al. (2009) Multi-sensor optimal data fusion for INS/GPS/SAR integrated navigation system. Aerospace Science and Technology 13: 232-237.
2. F Chen, Y Xu (2013) High-speed and robust scene matching algorithm based on ORB for SAR/INS integrated navigation system. Applied Mechanics & Materials 241-244: 439-443.
3. S Gao, Y Zhong, W Li (2011) Robust adaptive filtering method for SINS/SAR integrated navigation system. Aerospace Science and Technology 15: 425-430.
4. N Hoffmann, F Fuchs (2014) Minimal Invasive Equivalent Grid Impedance Estimation in Inductive-Resistive Power Networks Using Extended Kalman Filter. IEEE Transactions on Power Electronics 29: 631-641.
5. E Hatami, H Salarieh, N Vosoughi (2014) Design of a fault tolerated intelligent control system for a nuclear reactor power control: Using extended Kalman filter. Journal of Process Control 24: 1076-1084.
6. J Zhu, J Park, KS Lee, et al. (2008) Robust extended Kalman filter of discrete-time Markovian jump nonlinear system under uncertain noise. Journal of Mechanical Science and Technology 22: 1132-1139.
7. E Walker, S Rayman, R White (2015) Comparison of a particle filter and other state estimation methods for prognostics of lithium-ion batteries, Journal of Power Sources 287: 1-12.
8. D Sheinson, J Niemi, W Meiring (2014) Comparison of the performance of particle filter algorithms applied to tracking of a disease epidemic. Mathematical Biosciences 255: 21-32.
9. G Oppenheim, A Philippe, J de Rigal (2008) The particle filters and their applications. Chemometrics and Intelligent Laboratory Systems 91: 87-93.
10. B Zhang, M Chen, D Zhou, et al. (2007) Particle-filter-based estimation and prediction of chaotic states. Chaos, Solitons and Fractals 32: 149-1498.
11. JS Liu, R Chen (1998) Sequential Monte Carlo methods for dynamics systems. Journal of the American Statistical Association 93: 1032-1044.
12. R Srinivasan (2002) Importance sampling - Applications in communications and detection, Springer-Verlag, Berlin.
13. W Gao, J Li, L Shen (2011) Regularized particle filter for speech enhancement. Energy Procedia 13: 6161-6169.
14. Z Khan, T Balch, F Dellaert (2005) MCMC-based particle filtering for tracking a variable number of interacting targets. IEEE Transactions on Pattern Analysis and Machine Intelligence 27: 1805-1819.
15. G Pillonetto, BM Bell (2008) Optimal smoothing of non-linear dynamic systems via Monte Carlo Markov chains. Automatica 44: 1676-1685.
16. M Zhong, J Guo, Q Cao (2015) On Designing PMI Kalman Filter for INS/GPS Integrated Systems With Unknown Sensor Errors. IEEE Sensors Journal 15: 535-544.
17. S Hu, S Xu, D Wang, et al. (2015) Optimization algorithm for Kalman filter exploiting the numerical characteristics of SINS/GPS integrated navigation systems. Sensors 15: 28402-28420.
18. J Yin, J Zhang, K Mike (2007) The marginal Rao-Blackwellized particle filter for mixed linear/nonlinear state space models. Chinese Journal of Aeronautics 20: 346-352.
19. Y Zhong, S Gao, W Li (2012) A quaternion-based method for SINS/SAR integrated navigation system. IEEE Transactions on Aerospace and Electronic Systems 48: 514-524.