An Adaptive Neuro-Fuzzy Framework for Predicting the Likelyhood of Diabetes Mellitus

Abstract

Diabetes is a serious public health concern around the world, and its incidence is increasing on a daily basis, making it a global epidemic. Diabetes Mellitus affects around 442 million people globally. It has been anticipated that the prevalence will reach 55% by 2035, with an impact of one mortality every 6 to 10 seconds. Diabetes is spreading rapidly over the world, contributing to a high mortality rate. The purpose of this paper was to use adaptive Neuro-fuzzy to determine the blood glucose level of a diabetic patient. Data from the laboratories of 80 diabetes patients were collected at the Federal Medical Center Jalingo. Fasting blood sugar (FBS), genetic inheritance (GI), and body mass index (BMI) were used as input variables for the (ANFIS) model. For training and testing, a hybrid training method was used and the error obtained from the results is 0.63742 at epoch 4, indicating that the training performance is exactly 99.36%. Because of the exceptionally excellent accuracy rate, this demonstrates that the adaptive Neuro-fuzzy system can be used for medical diagnosis.

Keywords

Artificial Intelligence, Artificial Neural Network, Fuzzy Logic and Neuro-Fuzzy

Introduction

Diabetes is a chronic disease that occurs when the pancreas does not create enough insulin or when the body does not use the insulin that it does make adequately [1]. Hyperglycemia, or high blood sugar, is a typical side effect of untreated diabetes, and it can cause catastrophic harm to many of the body's systems, particularly the neurons and blood vessels [1]. Diabetes is classified into three categories. Type 1 diabetes mellitus, also known as insulin-dependent diabetes mellitus, arises when the pancreas fails to produce enough insulin. Type 2 diabetes mellitus, also known as insulin-independent diabetes mellitus, occurs when the body's ability to use insulin is impaired. Gestational diabetes is the third type [2]. A pre-diabetes patient has signs of diabetes but is not diabetic [3]. Diabetes will be the sixth largest cause of mortality in 2030, according to Cardner (2011). Globally, around 422 million individuals have type 2 diabetes mellitus, with this figure expected to climb to over 552 million by 2035. Diabetes is a relatively common condition among people of all ages, according to the World Health Organization (WHO) [4], and it has become a major health burden. With the increase in diabetic patients, there is a greater demand for a dependable and accurate system that can accurately diagnose diabetes in its early stages. Artificial Intelligence (AI) techniques such as artificial neural network, fuzzy logic and genetic algorithms has wide applications in medicine, and it has been found to have benefited medical diagnosis and decision support, various techniques and different systems have been proposed by researchers to diagnose diabetes using Artificial Intelligence (AI).

Suyash, Sharma, Kumar, and Darbari [5] sought to predict diabetes using an artificial neural network (ANN), and their model obtained 92% accuracy when evaluated with Pima Indian sample test data. Aruna, Pranav, Nerurkar, Ansari, and Bansode [6] used fuzzy logic to classify the risk level of major five diabetes complications such as vision loss, kidney failure, neuropathy, stroke diseases, and heart problems, and they achieved 92.5% accuracy for the prediction of major risk associated with diabetes. Baha, Adewumi, Blamah, and Wajiga [7] suggested a new model for predicting who will get type 2 diabetes. Their research's overarching purpose was to help to the government's endeavor to reduce morbidity and mortality rates associated with. The neural network experiment was set up using matlab 7.10.1. The neural network architecture consists of two hidden layers of 6 and 2 neurons and an output layer of I neuron. The network recorded the best validation performance of 0.1 00 at 532th epochs and a correlation coefficient of 0.9881.

As artificial intelligence in medical diagnostics has grown in popularity over the previous decade, much relevant research has been undertaken. Fuzzy logic (FL), artificial neural networks (ANN), genetic algorithms (GA), and other algorithms are examples of computational intelligence (CI) methodologies. This study used known literature to predict the presence of diabetes because there have been many previous studies on predicting the presence of diabetes mellitus. The majority of these research employ single CI components such as artificial neural networks, fuzzy logic, genetic algorithms, support vector machines, and others. This study aims to combine ANN and FL to create a neuro-fuzzy model that can predict the presence of diabetic Mellitus.

Method of data collection

The primary data was gathered through interviews with two medical workers to gain in-depth knowledge about diabetes Mellitus, while secondary data was gathered from laboratory technician's records on patients with diabetes mellitus at Federal Medical Centre Jalingo.

Adaptive neuro-fuzzy system

To construct an ANFIS model, three things are majorly involved; the architecture, the learning/training algorithm and performance evaluation of the model.

Architecture of the proposed model

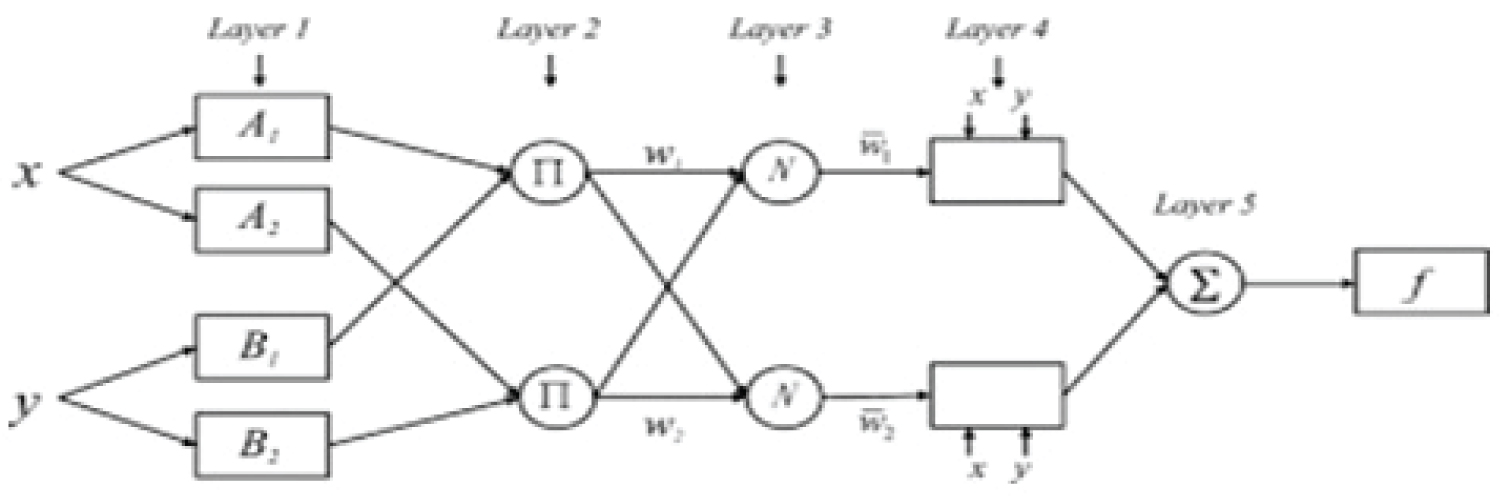
For the suggested model, the architecture proposed by Jang [8] and implemented on the Takagi-Sugeno architecture was used. This design employs a rule structure with a fuzzy antecedent and a functional consequent. The model used the Gaussian membership function for input membership function, and diabetic symptoms were assessed and used as model input parameters. Figure 1 depicts the architecture's five tiers.

The first layer

The first layer is as follows: This is referred to as the fuzzification layer. MFs are allocated to each input variable in this layer. The total number of MFs assigned to input variables is equal to the number of neurons in this layer. Each neuron in this layer is an adaptive node with a node function (the weights assigned to each neuron are modified during the learning process).

$$\begin{array}{l}{O}_{l,i}={\mu }_{Ai}\left(x\right),fori=1,2\\ or\\ O_{l,i}={\mu }_{Bi-2}\left(y\right),fori=3,4\end{array}$$

The MF types which can be assigned to the input variables are bell-shaped, Gaussian, triangular, trapezoidal and sigmoidal etc. The Gaussian membership function can mathematically expressed by as:

$$\mu \left(x_i\right)=\exp \left\{-\frac{1}{2}\left[\frac{{\left(x-c\right)}^2}{{\sigma }_i^2}\right]\right\}=e^{-\frac{1}{2}\left[\frac{{\left(x-c\right)}^2}{{\sigma }_i^2}\right]}$$

Here ‘i’ is equal to number of MFs assigned to each input. Where ‘ci’ and ‘σi’ are the center and width of the ‘ith’ Gaussian MFs. The shape of Gaussian MF depends on the value of premise parameters (‘ci’ and ‘σi’). These parameters are updated in the backward pass by back propagation gradient decent method on the basis of error produced during each training cycle.

The second layer: This is called the product layer or participation layer. Each neuron in this layer is non-adaptive and computes the product of incoming signals. Each node generates the firing strength of a rule.

$$O_{2,i}=w_i={\mu }_{Ai}\left(x\right){\mu }_{Bi}\left(y\right),i=1,2$$

The third layer: This is called the normalization layer. The nodes in this layer are non-adaptive and compute the normalized firing strength which is the ratio of firing strength of a rule to the sum of the firing strengths of all rules.

$$O_{3,i}=\overline{w_l}=\frac{w_i}{w_1+w_2},i=1,2$$

The fourth layer: This is called the defuzzification layer. Each node is adaptive and multiplies the normalized firing strength of a rule with corresponding first order polynomial function. In this layer, each node has a crisp output.

$$O_{4,i}={\overline{w}}_l{f}_i={\overline{w}}_l\left(p_{i}x+q_{i}y+r_i\right),$$

The fifth layer: This is called the output layer. It has only one node which is non-adaptive and sums up all incoming crisp signals to produce a single crisp output.

$$O_{5,i}={\displaystyle \sum _i{\overline{w}}_l}{f}_i=\frac{{\sum }_i{w}_{i}f}{{\sum }_i{w}_i}$$

Learning/training algorithm

The suggested model was trained using a hybrid technique that combines back propagation and the least mean square procedure. This hybrid technique will produce IF-THEN fuzzy rules automatically by analyzing the data and training the membership function using the least square approach and gradient descent (back propagation) method until the maximum number of epochs or minimum error tolerance is reached.

Model performance evaluation

The model performance has been evaluated using Root Mean Square Error (RMSE). This index estimates the residual between the actual value and desired value. A model has better performance if it has a smaller RMSE.

Development tools

This project has been implemented on a MATLAB R2018a environment using fuzzy logic toolbox and Gaussian membership function would be used throughout this experiment.

Proposed adaptive neuro-fuzzy system for diabetes prediction model design and structure

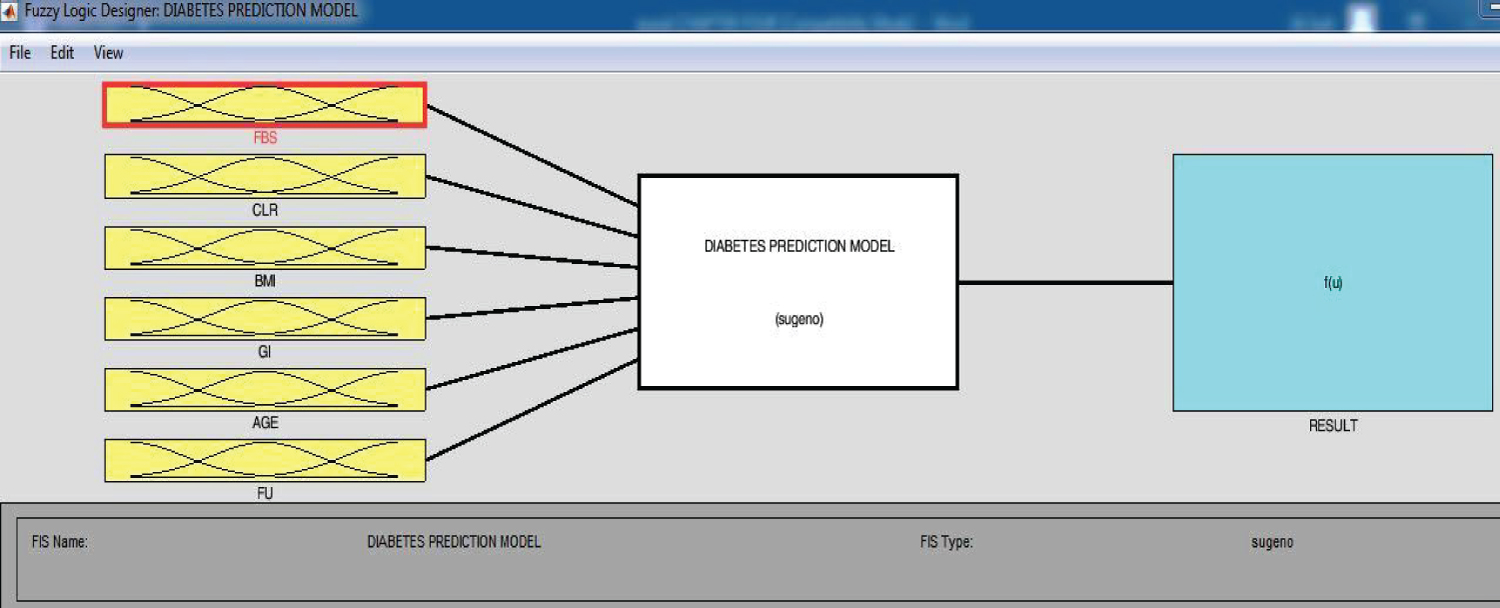
The ANFIS for diabetes prediction model was designed in MATLAB R2018b using fuzzy logic designer tool as shown in Figure 2. The structure of the model is depicted in Figure 2 below together with its associative membership functions.

Diabetes prediction ANFIS model structure

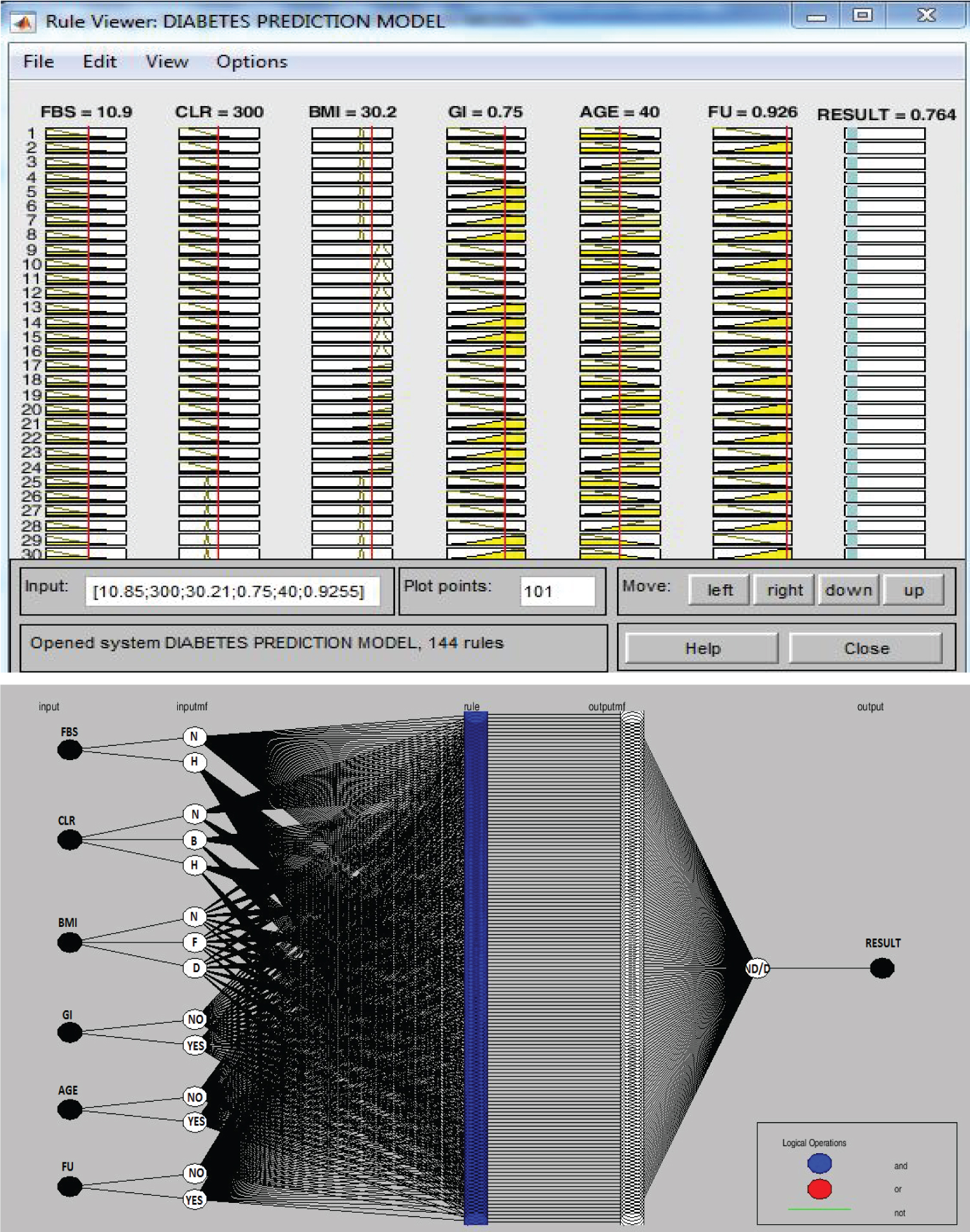
The structure and components of the ANFIS model for diabetes prediction is presented in Figure 3 below. It consists of six (6) inputs parameters fasting blood sugar (FBS), cholesterol (CLR), body mass index (BMI), genetic inheritance (GI), age (age), and frequent urinating (FU) on the left hand side, the Sugeno inference at the middle and diabetes prediction status as the output on the right hand side.

The model architecture has six (6) input parameters at the first layer, two (2) membership function (MF) of Fasting blood sugar (FBS) has two (2) membership function (MF), cholesterol (CLR) has three (3) membership function (MF), body mass index (BMI) has three (3) membership function (MF), genetic inheritance (GI) has two (2) membership function (MF), age (age) has two (2) membership function (MF), and frequent urinating (FU) has two (2) membership function (MF) (Table 1).

Conclusion

Diabetes is a chronic condition with numerous consequences that can be fatal. Diabetes self-management is a procedure that facilitates the knowledge, ability, and capacities needed to conduct managerial activities. Proper care is the only hope for many patients. Diabetes problems can be avoided if diabetes is detected early. The ANFIS model was utilized in this paper to diagnose diabetic illness. In medical applications, fuzzy set theory is useful in coping with uncertainty when making decisions. The use of fuzzy logic allowed us to incorporate uncertainty into the classifier design, increasing the trustworthiness of the system output. With six input characteristics, the ANFIS classifier was utilized to diagnose diabetes. The ANFIS model incorporated a neural network. The total classification accuracy of the ANFIS model was 99.36%. The results obtained demonstrated that the proposed ANFIS model can be used to diagnose diabetes.

References

1. Nesma S, Meryem S, Mohamed AC (2012) Interpretable classifier of diabetes disease. International Journal of Computer Theory and Engineering 4: 438-442.
2. Caipo Z, Jinjie S, Zhilong (2009) Fuzzy integral be applied to the diagnosis gestational diabetes mellitus. 41: 67-81 .
3. Ajmalahamed A, Nandhini KM, Krishna A (2014) Designing a rule based fuzzy expert controller for early detection and diagnosis of diabetes. ARPN Journal of Engineering and Applied Sciences 9: 819-827.
4. World Health Organization (2016) Fact sheet No. 312, Available online. Retrieved on 27 October, 2019.
5. Suyash S, Lokesh S, Vijeta S, et al. (2019) Prediction of diabetes using artificial neural network approach. Engineering Vibration Communication and Information Processing 478.
6. Aruna P, Nazneen A (2015) Risk prediction of disease complications in Type 2 diabetes patients using soft computing techniques: 2015 Fifth International Conference on Advances in Computing and Communications. 254-257.
7. Baha B, Adewumi A, Bulama N, et al. (2012) Artificial neural network to detect risk of type 2 diabetes. In: Proceedings of the 2012 ORSSA annual conference (20-30). South Africa. ORSSA. Retrieved August 21, 2019.
8. Jang JS (1993) ANFIS: Adaptive-network-based fuzzy inference system. IEEE transactions on Systems, Man, and Cybernetics 23: 665-685.