Cylindrical Panel Like Response of Fully Surface Parallel Restrained Simply Supported Hyperbolic Paraboloidal Thick General Cross-ply Panels
Abstract
An analytical (exact in the limit) solution to the boundary-value problem of deformation of a finite-dimensional general cross-ply thick hyperbolic-paraboloidal panel, modeled using a third order shear deformation theory, is presented. Of special interest is the issue of cylindrical panel-like response, in the presence of full surface-parallel constraints at all four edges of a thick antisymmetric cross-ply panel of negative Gaussian curvature. Interaction of the membrane action due to negative Gaussian curvature with the third order (respectively, first-order) bending-stretching coupling producing beam-column/tie-bar type softening/hardening effects in thick (respectively, thin) cross-ply panels also constitutes an important focus of this investigation.
Keywords
Third Order Shear Deformation Theory (TSDT), Thick Composite, Laminated Panel, Negative Gaussian Curvature, Hyperbolic-Paraboloidal Shell, Boundary Discontinuity, Double Fourier Series, Boundary-Value Problem, Complementary Solution, Asymmetric Cross-Ply, Bending-Stretching Coupling, Beam-Column Effect, Tie-Bar Effect, Membrane Action, Inter-laminar Shear Deformation
Nomenclature
a, b = Dimensions of the plate parallel to the x1 and x2 axes, respectively.
h = Total thickness of a laminated curved panel.
m, n = Modal wave numbers in x1 and x2 directions, respectively.
Ni, Mi = Surface-parallel stress resultants and moment resultants, respectively (i = 1, 2, 6).
Pi = Third order moment resultants (i = 1, 2, 6).
Qi, Ki =Transverse shear stress resultants and their third order counterparts, respectively (i = 1, 2).
Q = Distributed transverse load.
Ri= Principal radii of normal curvature of the reference (middle) surface in the xi direction.
ui = Components of displacement at the reference surface (x1, x2, 0) in xi direction (i = 1, 2).
xi = Orthogonal curvilinear coordinates.
φi = Rotation of the normal to the reference surface (i = 1, 2).
Introduction
Advanced fiber reinforced composites are finding ever increasing aerospace (as well as other) structural applications, prime examples being unmanned airborne vehicles (UAV), Boeing 787 Dreamliner (80% composite by volume, 50% by weight), F-35 JSF (Joint Strike Fighter, composites comprising 35% of airframe weight), F-22 Raptor (composites comprising 24% of the structural weight), Airbus A380 (composites more than 20% of airframe) among others. A reliable design/analysis of these critical structural components must account for through-thickness variation of transverse shear strains or stresses. This is because the matrix material is of relatively low shearing stiffness as compared to the fibers, which render polymeric composite shell type structures highly vulnerable to transverse shear related fatigue failures. Finally, additional, and severer complexities arise when a solution to the boundary-value problem of deformation of arbitrarily laminated saddle-shaped shells of finite dimensions is sought. The present study seeks to meet this challenge through analysis of a model laminated shell boundary-value problem, which requires, unlike either two centuries-old Navier's or close to a century-old Levy's approach, satisfaction of prescribed (admissible) boundary conditions at all four edges.
Since manufacturing technology of composites offer designers many-fold configurational flexibility to boost performance, the above-mentioned structural components must, by necessity, embrace complex shapes involving compound curvatures, including those with negative Gaussian curvature. Shells of negative Gaussian curvature, although having been paid far less attention in the structural mechanics literature compared to their non-negative counterparts (e.g., spherical and cylindrical shells), are quite frequently encountered in civil structural and other terrestrial applications, the most prominent examples being hyperbolic-paraboloidal shells (saddle type roof structures) and hyperboloidal shells of revolution (e.g., cooling towers), pioneered by Shukov, inspired by the mathematical work of Chebyshev and Lobachevsky. In spite of their innate architectural elegance, such structural shapes suffer from the shortcomings of their natural frequencies or critical (buckling) loads being lower than their non-negative Gaussian counterparts. This notwithstanding, such deficiencies are arguably more than compensated by their stable post-buckling response ("for sufficiently strong boundary conditions") as well as for being less sensitive to localized initial imperfections such as dents or dimples. The stability of thin shallow shells with negative Gaussian curvature was first investigated by Ermolenko and Kornev [1], their greatest interest being shells with negative Gaussian curvature that are almost cylindrical. Aksu [2] has formulated a shell element with negative Gaussian curvature that is applicable for both thin and moderately thick shell analysis.
Thermo-mechanical problems of bending, vibration, buckling and post-buckling sometimes resulting in localization/delocalization of buckling patterns and shear crippling type propagating instability and compression fracture of isotropic as well as laminated anisotropic plates and shells of practical interests are, in general, solved mostly by numerical methods, such as the finite element methods (FEM) [3-31], although a few semi-analytical studies are also available [32-34]. The finite element methods are among the most preferred approaches, because of the ease with which issues relating to nonlinearity, general plate/shell geometry, geometric irregularity, thickness non-uniformity, anisotropy, arbitrary lamination, complex boundaries involving multiple holes or cut-outs, general loadings and so on, can be handled by this class of methods; see e.g., [3-31], and references therein among numerous others.
These weak or integral form of solutions are typically validated by comparing with their analytical (i.e., strong or differential form of solutions) counterparts, which are either exact (i.e., closed-form) or exact in the limit (e.g., Fourier series solutions), and which serve as bench-mark solutions for validation of approximate numerical solutions, such as those computed using the FEM. In principle, the above-mentioned variational or weighted residual type numerical procedures, such as the FEM, are known to be capable of satisfying the system of governing PDE's in some weak sense, and also the boundary limits (traces) of the solutions can be said to exist in some weak sense (trace theorem) and agree with the prescribed boundary data in some suitable function space, such as the Sobolev space, , wherein the superscript 0 refers to the boundary. However, they fail to satisfy, in the point-wise sense (), all the boundary conditions, especially the natural boundary constraints, and produce averaged out results across boundary discontinuities of unknown functions and/or their partial derivatives.
Investigations based on first the classical lamination theory (CLT), and thereafter first-order shear deformation theory (FSDT) for solving laminated shell boundary-value problems using various approximate techniques are too numerous to list here (for brief literature reviews, see Reddy [6] and Chaudhuri, et al. [35] for the former, while refer to Reddy [6], and Chaudhuri and Kabir [36] for the latter). Especially, Kapania [37] and Qatu [38] have presented extensive surveys on various aspects of laminated shells during their earlier (before 1989) and later phases of development, respectively. Double Fourier series solutions to classical lamination theory (CLT)-based homogeneous and laminated plate and shell boundary value problems are available in [39-44] and [45-48], respectively. Likewise, double Fourier series-based solutions to various first order shear deformation theory (FSDT)-based laminated anisotropic plate and shell boundary-value problems have been presented in [49-57] and [58-64], respectively.
Basset [65] appears to have been the first to suggest that the displacements can be expanded in power series of the thickness coordinate, x3 = . More recently, second- and third order shear deformation theories (TSDT), involving continuous in-plane/surface-parallel displacements distribution through the thickness of thick laminated plates/shells, have become available in the literature to account for the through-thickness shear deformation. A thorough review on the historical development of TSDT-based laminated plates/shells is available in Reddy [6], Chaudhuri and Kabir [66] for the earlier years, and Oktem and Chaudhuri [67,68], Chaudhuri and Oktem [69] and Giunta, et al. [70] for the more recent development on this topic.
Navier type solutions to various third order and other type (e.g., trigonometric) of shear deformation theories, which can at best be regarded as particular solutions, have been extensively employed in the literature; see, e.g., Reddy [6], and Mantari, et al. [71]. Boundary-discontinuous type double Fourier series solutions, in contrast, constitute complete (complementary and particular) solutions to the boundary-value problems of TSDT-based cross-ply laminated plates and shells [67-69]. The precise mathematical premises of the boundary-discontinuous type double Fourier series approach to solution of completely coupled system of partial differential equations subjected to admissible general boundary conditions are available in Chaudhuri [72,73]. Levy-type solutions [74-77] to thick cross-ply flat and curved panels serve as special cases of the above. Additionally, Levy type solutions (derived in conjunction with the state space concept) to symmetrically laminated anisotropic plates are available in Khdeir and Librescu [78]; see also Reddy [6].
Oktem and Chaudhuri [79] have shown that the elastic responses of the present TSDT-based cross-ply spherical panels are in qualitative agreement with their zigzag or LCST (layer-wise constant shear angle theory)-based counterparts, computed using finite element methods (FEM) [7]. It also is worthwhile to note here that the zig-zig or layer-wise shear deformation theory, first introduced by Mau, et al. [3] in the finite element context, and subsequently followed up by Seide [80], Chaudhuri [81-84], and Chaudhuri and Seide [4,82,83], have been found to be very useful for obtaining numerical (e.g., FEM) solutions to laminated thick plate and shell problems; see also, e.g., Carrera [85], Chaudhuri [86-88], Demasi [89] among others for later follow-up studies.
A few experimental verification studies are also worth mentioning in the interest of completeness of the literature review. Bert and Mayberry [90] have reported comparisons of natural frequencies computed using the approximate Raleigh-Ritz technique with their experimental counterparts. Chaudhuri, et al. [91], and Chaudhuri and Balaraman [92] have presented both manufacturing techniques and experimental investigations, as well as comparisons of experimentally determined natural or resonant frequencies of thin symmetrically laminated anisotropic GFRP (glass fiber reinforced plastic) plates having different boundary conditions, with their counterparts, computed using sophisticated analytical techniques such as the boundary-continuous displacement type Fourier series method. Li, et al. [93] have employed the laser linear scanning method to measure the modal shape of a fiber-reinforced composite thin plate.
Finally, Chaudhuri, et al. [94,95] have recently addressed the issue of hyperbolic-paraboloidal or saddle-shaped thick cross-ply panels with Levy type boundary conditions, where the prescribed boundary conditions on two opposite edges are satisfied a priori. Although analytical solutions to the problems pertaining to thick symmetrically laminated panels with negative Gaussian curvature, where the prescribed boundary conditions need to be satisfied at all four edges, have recently been made available [96-97], their asymmetrically laminated counterparts have till recently [98] been absent in the literature, which is the primary objective of the present investigation. In what follows, a heretofore unavailable TSDT-based boundary-discontinuous double Fourier series solution to the boundary value problem of saddle-shaped cross-ply panels, with the SS4 type simply supported boundary condition, prescribed at all four edges, is derived. The significance of four different types of simply supported boundary constraints is well-known in structural mechanics literature [99]. While the SS1 boundary constraint is a two-dimensional (mathematical model) extension of the roller type simple support of a beam, the SS4 can be considered to be a similar extension of the hinge type simple support of beam-like (e.g., bridge) structures. The single most important factor to the commercial and military aircraft and rocket motor case designers alike is, of course, the design flexibility inherent in these composite laminates, known as tailoring, which is essentially exploiting the possibility of obtaining optimum design through a combination of structural/material concepts, such as stacking sequence, choice of the component phases, etc., panel-edge restraints (or lack thereof) to meet specific design requirements. In the context of simply supported panel edge constraints, the responses of panels with the SS1 and the SS4 boundary conditions represent the two bounds, and the rest (i.e., SS2 or SS3) lies somewhere in between. Since the flattening effect of negative Gaussian curvature on simply supported thick asymmetrically laminated cross-ply panels in the absence of surface-parallel edge restraints (SS1, say the upper bound) has already been investigated [98], it is important to see what the other extreme (SS4, say the lower bound) would look like under a similar condition. Both R1(-) type and R2(-) type saddle shaped panels behave more like flat plates, because of the compensating effect of two opposite curvatures in such panels, in the absence of surface-parallel edge restraints (SS1) [98]. This fact can be exploited by designers in order to tailor the response of a composite panel with negative Gaussian curvature. The goal of the present investigation is to exploit the SS4 counterpart of the same purpose.
Section 2 presents the statement of the problem under investigation, while some of the details thereof are described in Appendices A, B and C. Specifically, the Euler-Lagrange equations representing the equations of equilibrium, and the associated admissible boundary constraints for the present TSDT, both derived using the principle of virtual work, are presented in Appendix A. Appendix B shows some of the constants that appear in the equations, while the classification of four different types of simply supported or clamped boundary constraints for the present TSDT, obtained from Appendix A, is presented in Appendix C. Section 3 supplemented by Appendix D presents the implementation of the boundary-continuous double Fourier series to analytically (exact in the limit) the boundary-value problem stated above. In Section 4, novel numerical results are presented to understand the complex deformation behavior of simply supported (SS4) antisymmetric cross-ply panels with negative Gaussian curvature. The intricacies of the interaction of the SS4 type simply supported boundary condition, which entails full surface-parallel boundary constraints, with the effect of negative Gaussian curvature have so far remained unaddressed in the literature. Comparison of these results with their cylindrical and spherical counterparts is intended to demonstrate the effect of Gaussian curvature on the deflections and moments of these saddle-shaped panels. Of special interest is the issue of effect of negative Gaussian curvature, in the presence of full surface-parallel constraints at all four edges, on the cylindrical panel-like response of a thick asymmetrically laminated cross-ply panel. Interaction of the membrane action due to negative Gaussian curvature with the third order (respectively, first-order) bending-stretching coupling producing beam-column/tie-bar type softening/hardening effects in thick (respectively, thin) cross-ply panels also constitutes an important focus of this investigation. Some interesting, including what may be construed to be somewhat counter-intuitive, conclusions drawn from the present investigation are presented in Sec. 5, In addition, extensive suggestions for future research of laminates of negative Gaussian curvature are provided in Section 6.
Statement of the Problem
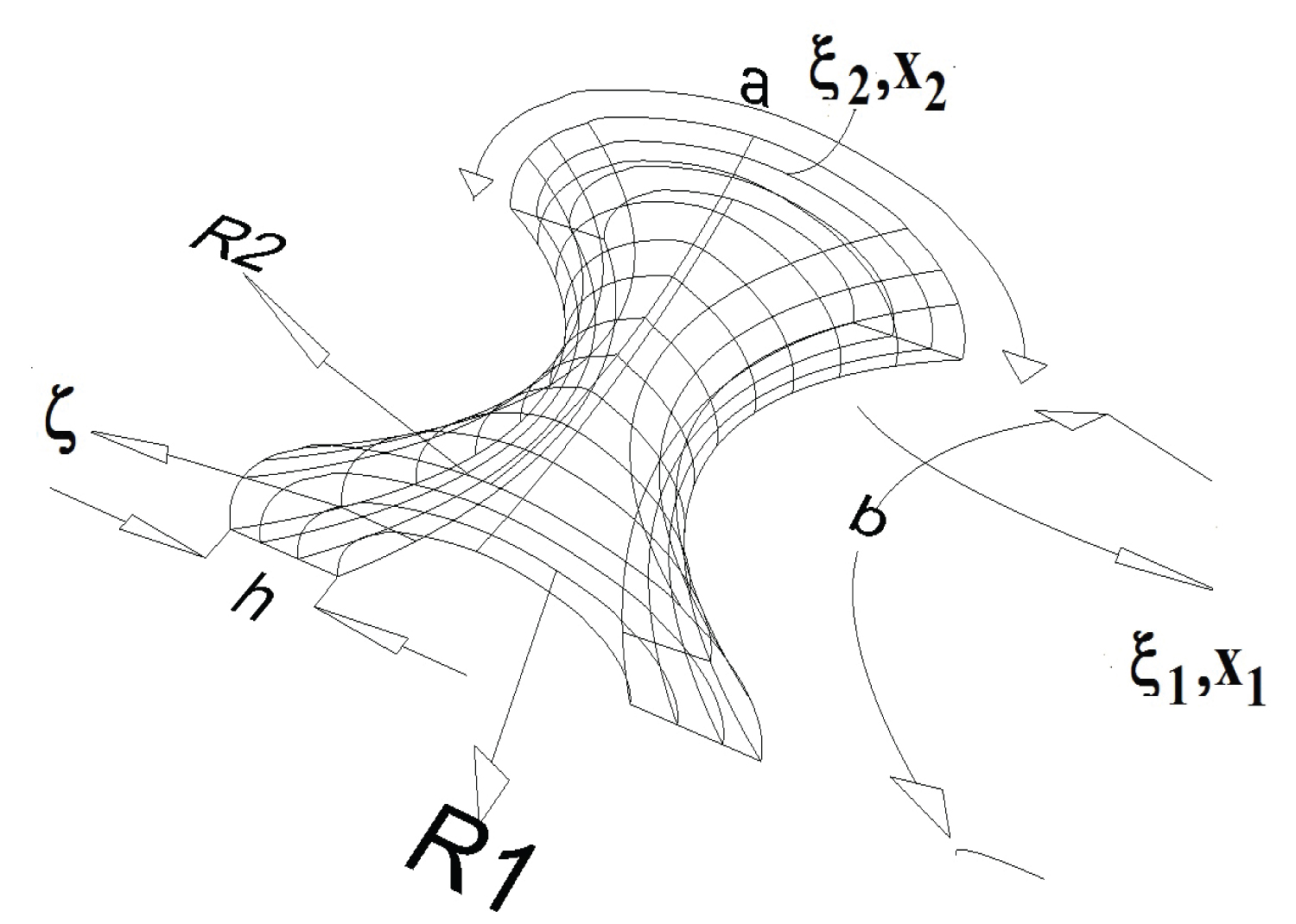
The orthogonal curvilinear coordinates (1, 2, 3 = ) are attached to the mid-surface of a shell of negative Gaussian curvature, as shown in Figure 1. The 1 and 2 curves are lines of curvature on shell mid-surface, = 0, while is a straight line normal to the mid-surface. The cross-ply shell under consideration is composed of a finite number of orthotropic layers of uniform thickness. Strain-displacement relations from the theory of elasticity in curvilinear coordinates are given by [100]:
in which [41]
In Eq. (1), the top sign of either ± or ∓ represents convex upward type curvature, while the reverse is true for the bottom sign, and represents the components of the strain tensor, and (i =1, 2, 3) denotes the components of the displacement vector along the (1, 2, 3 = ) coordinates at a point, (x1, x2, x3 = ). The principal radii of normal curvature of the reference (middle) surface are denoted by R1 and R2, while RG1 and RG2 represent the geodesic curvatures of 1 and 2 curves, respectively [88]. In order to model the kinematic behavior of the shell, an additional set of simplifying assumptions are invoked: (i) Transverse inextensibility, (ii) Moderate shallowness (in regard to the normal curvatures), and (iii) Negligibility of geodesic curvature. The last two assumptions permit the use of curved panel coordinates x1, x2, x3 = , attached to the panel mid-surface. It may be noted that for a cylindrical shell, the lines of principal curvature coincide with the surface-parallel coordinate lines, while for a spherical or hyperbolic-paraboloidal shell, the same can be assumed upon negligence of the geodesic curvatures of the coordinate lines.
The surface-parallel displacements can be expanded in power series of 3 = as suggested by Basset [65]. Only keeping the cubic terms and satisfying the conditions of transverse shear stresses (and hence strains) vanishing at a point (, 2, ± h/2) on the outer (top) and inner (bottom) surfaces of the shell, yields [6,66,77].
where denotes the displacements of a point on the middle surface, while and are the rotations at = 0 with respect to the 2 and 1 axes, respectively. The corresponding kinematic relations are given by
in which
For a general cross-ply (symmetric and antisymmetric being two special cases) shell, the following elastic rigidities (integrated stiffnesses), given by Eqs. (A6) in the Appendix A, are zero:
The stress resultants, moment resultants and higher-order moment and shear resultants, given by Eqs. (A5) in terms of components of displacement and rotation, can now be written as follows:
The constants, , referred to Equations (6), are given in Appendix B.
Substitution of Equations (7) into equilibrium equations given by Eqs. (A3) supplies the following five highly coupled fourth order governing partial differential equations [69,73]:
where ai, ei and fi are constants, which are given in Appendix B.
In what follows, the above system of five partial differential equations is solved in conjunction with the SS4 type simply supported boundary condition, prescribed at the edges, , a, and, , b, which are given as follows:
SS4 type simply supported boundary condition, prescribed at the edges, a and b which are given as follows (Refer to (Figure 11), and Equations (C1) and (c2d) in Appendix C):
Solution Methodology
The particular solution to the boundary-value problem of a TSDT-based cross-ply shell, with the SS4 boundary condition prescribed at all four edges, is assumed as follows:
Where,
The total number of unknown Fourier coefficients introduced in Eqs. (10) enumerate to 5 mn+2m+2n. The next operation is comprised of partial differentiation of the assumed particular solution functions. The procedure for differentiation of these functions is based on Lebesgue integration theory that introduces boundary Fourier coefficients arising from discontinuities, known as complementary boundary constraints [72,73], of the particular solution functions at the edges x1 = 0, a, and x1 = 0, b. As has been noted by Chaudhuri [70], the boundary Fourier coefficients serve as complementary solution to the problem under investigation. The procedure imposes certain boundary constraints in the form of equalities and complementary boundary constraints in the form of inequalities, the details of which are available in Chaudhuri [72,73], and will not be further discussed here in the interest of brevity of presentation. The partial derivatives, which cannot be obtained by term-wise differentiation, are obtained as follows. The above function u1 and its first partial derivative, obtained by term-wise differentiation, are not satisfied at the edges, x1 = 0, a, thus violating the boundary constraints and complementary boundary constraints, respectively, at these edges. Therefore, u1 is forced to vanish at these edges (boundary constraints), while for further differentiation, is expanded in double Fourier series, in the form suggested by Chaudhuri [72,73], in order to satisfy the complementary boundary constraint (inequality). The partial derivatives are then obtained as follows [73].
In a manner similar to , is forced to vanish at the edges, and b. The derivatives of are given as follows:
in which
and the boundary Fourier coefficients, and are defined in Appendix D. The remaining partial derivatives can be obtained by term-wise differentiation. The above step generates additional 2m+2n (unknown) boundary Fourier coefficients.
Introduction of the displacement functions and their appropriate derivatives into the governing partial differential equations will supply the following 5 mn + 2m + 2n equations:
Satisfying the geometric boundary conditions given by Eqs. (9c, d), i.e., those pertaining to vanishing of u1, and u2 at the appropriate edges, and equating the coefficients of sin(αx1), cos(βx2) etc. yield the following algebraic equations:
For all values of
1.
For all values of m = 1,2,.........
2.
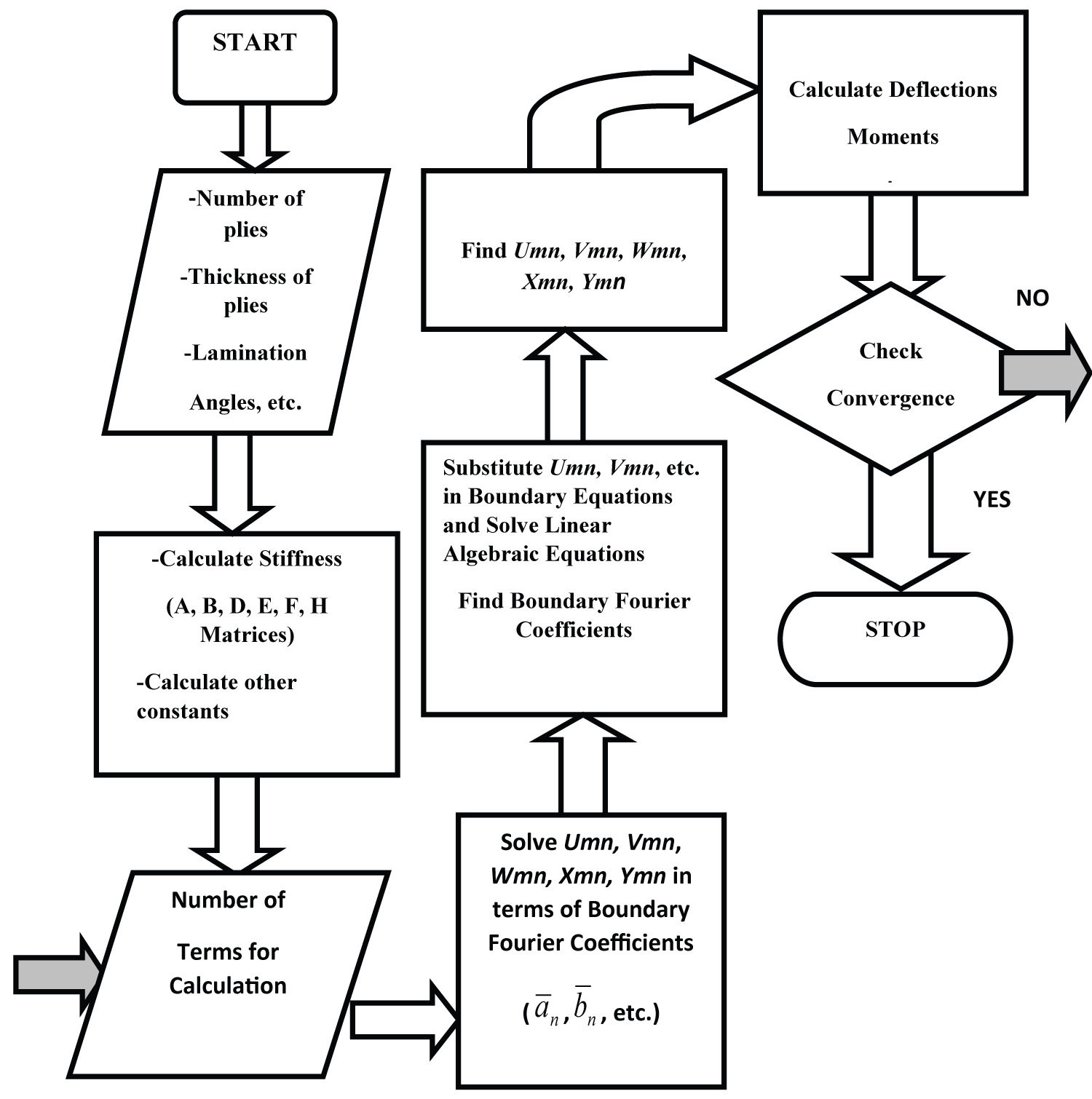
The geometric boundary conditions, given by Eqs. (9a), relating to u3 are satisfied as a priori at the edges, x1 = 0, a, and x2 = 0, b. Similarly, the rotations φ1 and φ2 also satisfy the boundary conditions, given by Eqs. (9b) a priori. The natural boundary conditions relating to M1, M2, P1, and P2 and given by Eqs, (9e, f) are also satisfied as a priori. This step generates additional 2m+2n equations for the solution. Finally, the above operations result in, in total, 5mn + 4m + 4n linear equations in as many unknowns. In the interest of computational efficiency, Eqs. (15) are solved for , and Equations (16) for and , in terms of the unknown boundary Fourier coefficients and , defined in Eqs. (D1a, b) below [69,77,101], in a manner outlined in Figure 2. These Fourier coefficients are then substituted in natural boundary conditions, given by Equations (17), thus reducing the size of the matrix to be inverted by orders of magnitude (from a system of 5mn + 4m + 4n to that of 2 m+2 n equations in as many unknowns) depending on the cut-off values of m and n. Resulting equations are finally solved for boundary Fourier coefficients and , using a MATLAB (version R2014b) code developed by the authors. When and vanish, the Navier type solution due to Reddy [6] is recovered.
Numerical Results and Discussions
Results obtained using the present boundary-discontinuous Fourier analysis for ss4 boundary conditions prescribed at all four edges
To illustrate the validity of the analytical procedure presented in the preceding section, the present study investigates cross-ply panels, with negative Gaussian curvature and of square plan-form (a = b). These panels assume the form of saddles, and are subjected to uniformly distributed transverse load, q0 = 1MPa (145.038 psi) applied to a central patch covering one-fourth of the top surface area (patch load); (Figure 3a and Figure 3b), (Figure 4a and Figure 4b), (Figure 5a and Figure 5b), (Figure 6a and Figure 6b) and (Figure 7a and Figure 7b) below. For comparison purposes, results for panels under full uniform load are also presented; (Figure 8a and Figure 8b), (Figure 9a and Figure 9b), (Figure 10a and Figure 10b) and (Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9). The following material properties are assumed: E1 = 175.78 GPa (25,000 Ksi), E1/E2 = 25, G12/E2 = G13/E2 = 0.5, G23/E2 = 0.2, ν12 = 0.25, in which E1 and E2 are the surface-parallel Young's moduli in x1 and x2 coordinate directions, respectively, while G12 denotes surface-parallel shear modulus. G13 and G23 are transverse shear moduli in the x1-x3 and x2-x3 planes, respectively, while ν12 is major Poisson's ratio on the x1-x2 surface. It may be remarked that the shear moduli display nonlinear characteristics [99,102]. An expression for the nonlinear shear modulus, G12 (=G13) is derived, by Chaudhuri [102] based on the assumption of uniform distribution of micro-kinks and fiber misalignment defects. Fiber micro-kinking is caused by crystallite disorientations, as detected by the Raman [103] and X-Ray measurements, inside a carbon fiber. This said, this type of material nonlinearity can be ignored for small deflection analysis of polymer matrix composite (PMC) structural elements without much loss of accuracy (in the interest of analytical convenience). However, material nonlinearity must be accounted for analysis of metal matrix composite (MMC) structural elements, e.g., boron/aluminum tubes [104]. The following normalized quantities are defined:
in which 'a' denotes the length of one side of the panel of square plan-form and is taken to be equal to 812.8 mm (32 in.). For all the numerical results presented here, the displacement, u3, and moment, , are computed at the center of the panel. Before presenting numerical results for saddle-shaped panels, those pertaining to symmetric and anti-symmetric cross-ply (R1 = R2 = ∞) plates [101] as well as spherical (R1 = R2) panels [69], with the same boundary conditions have been reproduced first. Additionally, (Figure 8) of Oktem and Chaudhuri [101] displays the convergence (with m = n) of normalized transverse displacement (deflection), and moment, , of a moderately thick (a/h = 10) antisymmetric cross-ply [0/90] plate, computed using the present TSDT. Both the central deflection, and central moment, , exhibit very rapid convergence at m = n ≤ 5.
Similar rapid convergence is observed for their spherical panel counterparts for m = n ≤ 10 in Figure 2 of Chaudhuri and Oktem [69]. For the distributed patch load, applied over one-fourth of the area of the panel, the applied pressure term used in the computation is given as follows:
where = = a/4, for patch load and = a, for uniform load.
Effects of curvature: Comparison of response of curved panels of negative, zero and positive gaussian curvature
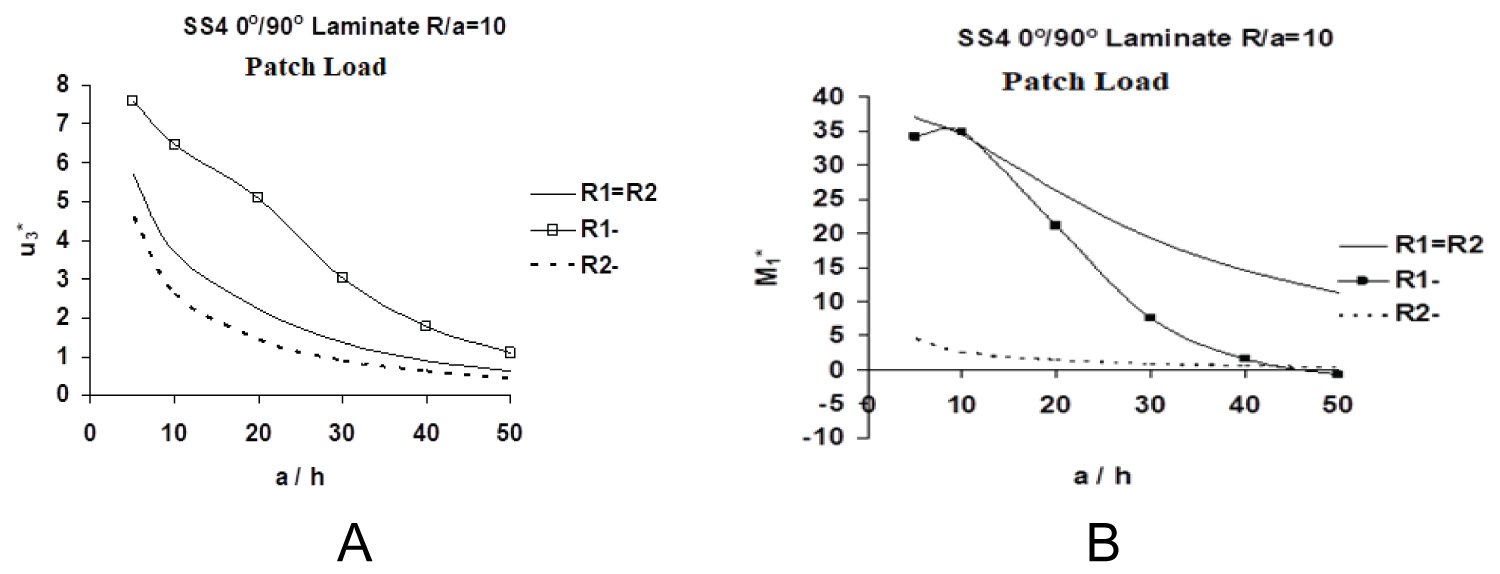
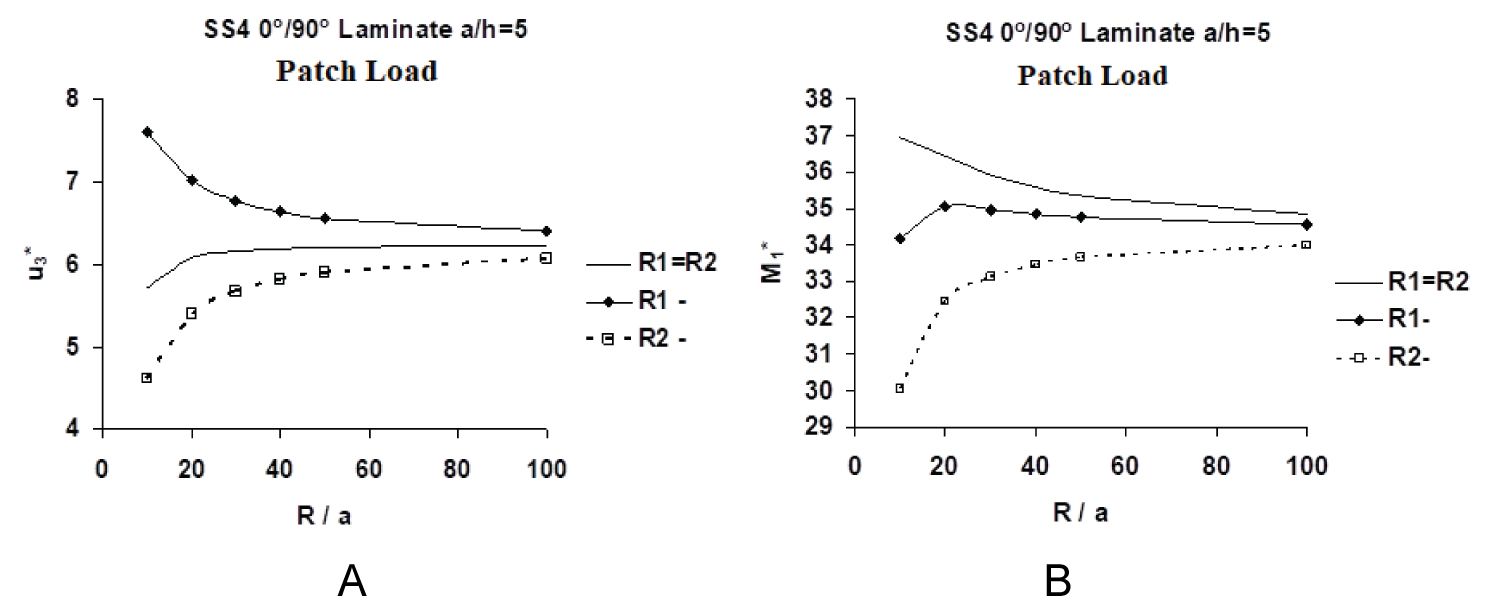
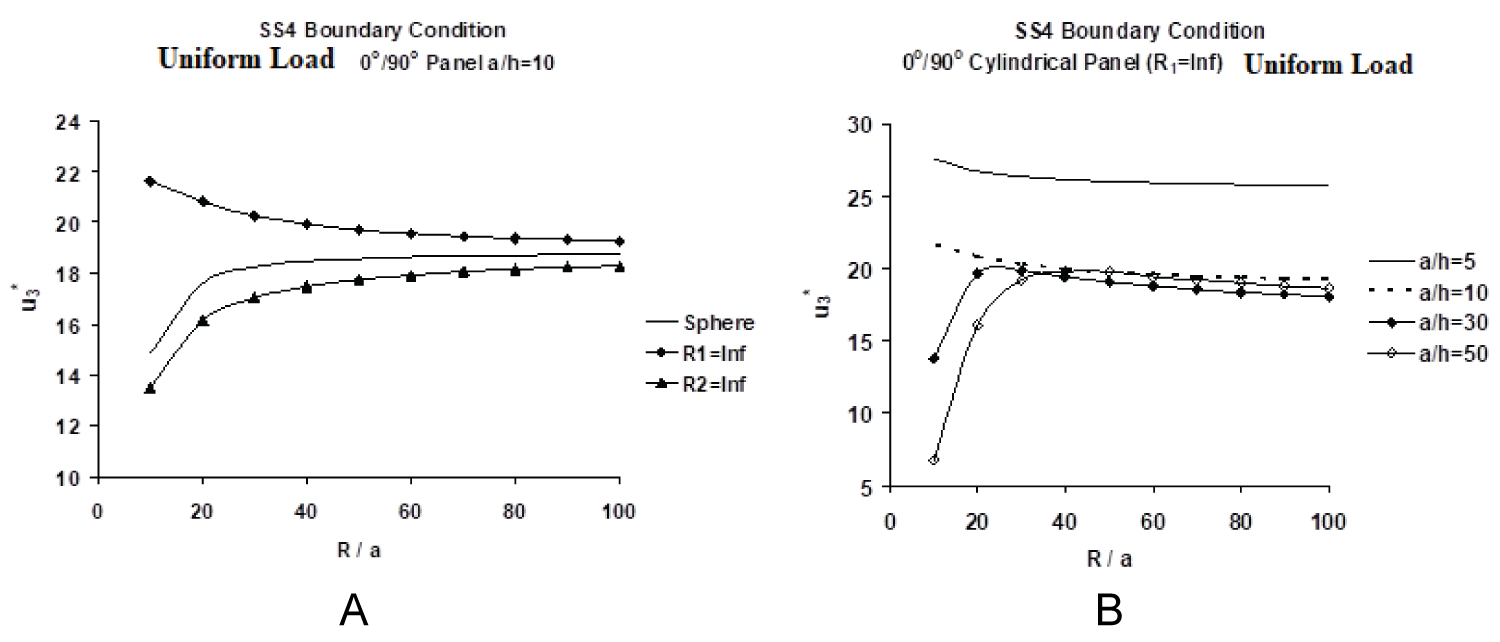
Figure 3a presents the variations of normalized central deflections, , of antisymmetric [0/90] hyperbolic-paraboloidal or saddle-shaped (negative Gaussian curvature, R = R1 = - R2) as well as spherical (R = R1 = R2) moderately deep (R/a = 10) panels (under patch load) with a/h ratio. It is interesting to note from Figure 3a that [0/90] saddle shaped R1(-) and R2(-) panels as well as their spherical (R1 = R2) counterpart experience steadily decreasing normalized deflections, with increase of a/h. The results for the spherical panel lie in between their two saddle-shaped counterparts, with saddle shaped panel, R1(-), exhibiting greater flexibility (beam-column effect), while the panel, R2(-), displaying more reduced response (tie-bar effect) Table 1 displays the same trend for the uniform load. These results provide a clear indication of the beam-column/tie-bar effects, arising out of bending-stretching coupling, in both the R1(-) and R2(-) type panels, which has a complex interaction with the membrane action, caused by the curvature effect, in the presence of surface-parallel edge restraint (SS4 boundary condition). It is interesting to point out here that there are two types of bending-stretching coupling in the TSDT: (i) Third order bending-stretching, which arises out of non-vanishing Eij's, that can only be captured by the TSDT, and (ii) First-order bending-stretching coupling, caused by non-vanishing Bij's, which is generally covered by all laminated shell theories. The latter type has been investigated in-depth in the context of axi-symmetric deformation of thin [35,105,106] as well as moderately thick [107-109] variously laminated cylindrical shells, in addition to static and dynamic tests on flat laminates [91,92,110]. It is further noteworthy in this context that the bending-stretching coupling may either cause surface-parallel compression ("beam-column" effect) or surface-parallel stretching (called "tie-bar" effect) in a panel subjected to bending. The former has a softening effect while the latter has a stiffening or hardening effect on the laminated panel response [106]. In this context it is interesting to observe that the response of a saddle shaped [0/90] R1(-) type panel closely resembles that of a [0/90] cylindrical panel (R1 = ∞), displayed in Figure 8a, wherein stiffening effect of the membrane action is largely compensated by the softening action of the beam-column effect, caused by the bending-stretching coupling rigidities (primarily Eij's and also Bij's), acting in concert with the surface-parallel edge restraint (imposed by the SS4 boundary condition). Likewise, the response of a saddle shaped [0/90] R2(-) type panel closely resembles that of a [0/90] cylindrical panel (R2 = ∞), shown in Figure 8b, with the game-changer of the stiffening effect of the membrane action now being in sync with the hardening action of the above-mentioned tie-bar effect, however acting in opposition to the surface-parallel edge restraint (SS4 boundary condition). Table 1 and Table 5 validate this statement when all the panels are subjected to uniform loading, for at least up to a/h = 20.
Variations of normalized central deflections, , of symmetric [0/90/0] saddle-shaped (negative Gaussian curvature, R = R1 = - R2) as well as spherical (R = R1 = R2) moderately deep (R/a = 10) panels with a/h ratio are presented in Figure 2a of Chaudhuri and Oktem [97]. All three shell geometries exhibit the same response in the entire range of a/h ratios, because of the absence of beam-column/tie-bar effects. The same trend is valid for the uniform load, as attested by the results displayed in the fifth, sixth and seventh columns of Table 2. In addition, Figure 2a of Chaudhuri and Oktem [97] also shows that all three panels exhibit progressively stiffer response (i.e., progressive reduction of the shear deformation effect) with the increase in a/h ratio, in the thinner shell regime [7].
Figure 3b presents variations of normalized central moments, , of antisymmetric [0/90] saddle-shaped (negative Gaussian curvature, R = R1 = - R2) as well as spherical (R = R1 = R2) moderately deep (R/a = 10) panels with a/h ratio, under patch loading. The normalized central moment, , of saddle shaped [0/90] R1(-) type panels, first increases with a/h in the thick shell regime, reaches its maximum at a/h = 10, and thereafter progressively decreases in the thinner shell regime, even assuming slightly small negative values for a thin laminate (a/h = 50). of spherical panels, in contrast, steadily decreases with a/h, and is higher for the most parts than its sadde-shaped counterparts. Interestingly, of the saddle shaped [0/90] R2 (-) type panels also decreases progressively with a/h, but its magnitude is much smaller than those of the remaining two panels. The same trend is valid for the uniform load, as attested by the results displayed in the fifth, sixth and seventh columns of Table 3. As discussed above, curves of the saddle-shaped [0/90] R1(-) and R2 (-) type panels somewhat resemble their respective cylindrical (R1 = ∞) and (R2 = ∞) counterparts (not shown here). Table 3 and Table 7 validate this statement when all the panels are subjected to uniform loading, for at least up to a/h = 20.
Again, variations of normalized central moments, of symmetric [0/90/0] saddle-shaped (negative Gaussian curvature, R = R1 = - R2) as well as spherical (R = R1 = R2) moderately deep (R/a = 10) panels with a/h ratio are presented in Figure 2b of Chaudhuri and Oktem [97]. of all three [0/90/0] panels first rises rapidly with a/h in the thick shell regime, then reaches a peak in the moderately thick shell regime, and finally drops rapidly as the shell gets thinner. The same trend is valid for the uniform load, as attested by the results displayed in the fifth, sixth and seventh columns of Table 4.
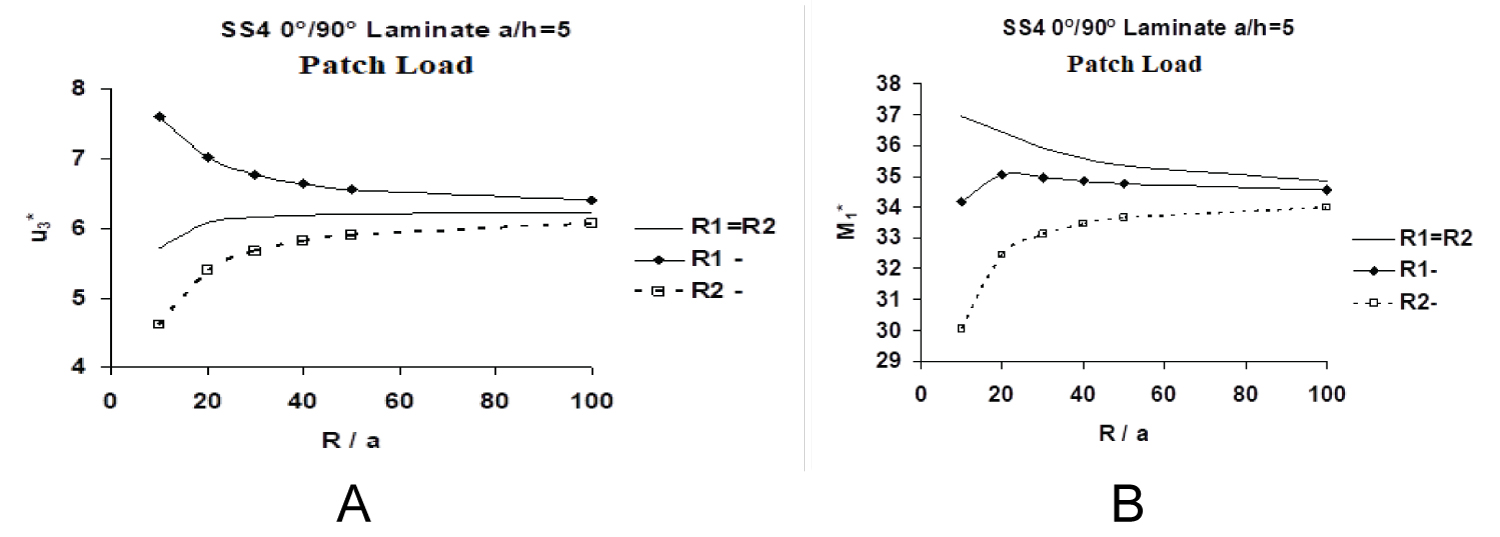
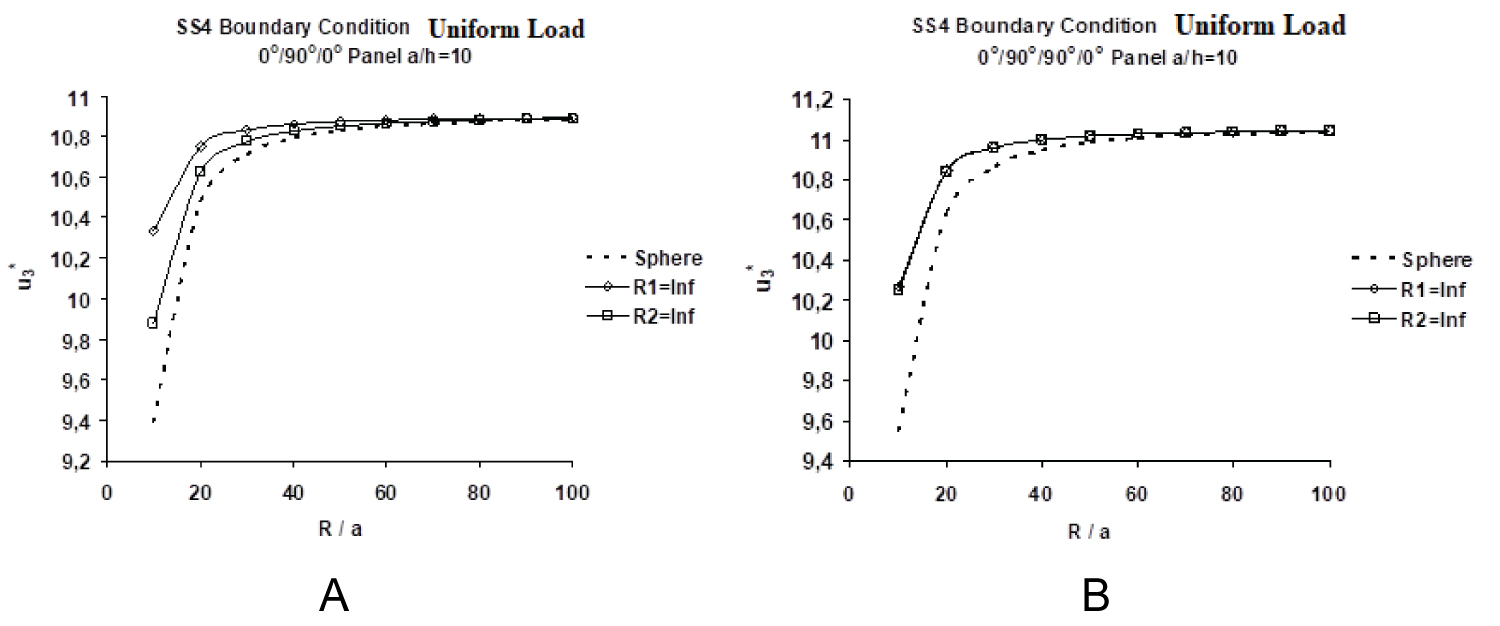
Variations of normalized central deflections, of [0/90] spherical as well as saddle shaped R1(-) and R2(-) type thick (a/h = 5) panels, with the R/a ratio, are presented in Figure 4a. Curvature effect (membrane action) is also responsible for the reduction in for R/a < 20. It is noteworthy, as is exhibited in Figure 4a, that the curvature effect (membrane action) enhances the normalized deflection of a saddle shaped [0/90] R1(-) type panel, which, as has been discussed above, closely resembles that of a [0/90] cylindrical panel (R1 = ∞), displayed in Figure 9a (and also in Figure 9b for a/h = 5 and 10), wherein stiffening effect of the membrane action is largely compensated by the softening action of the beam-column effect, caused by the bending-stretching coupling rigidities (Eij's and Bij's), acting in concert with the surface-parallel edge restraint (imposed by the SS4 boundary condition). In contrast, the same action decreases the normalized response of its saddle shaped [0/90] R2 (-), which, as mentioned above, closely resembles that of a [0/90] cylindrical panel (R2 = ∞), also exhibited in Figure 9a, with the game-changer of the stiffening effect of the membrane action now being in sync with the hardening action of the tie-bar effect (caused by the bending-stretching coupling rigidities, Eij's and Bij's), however now acting in opposition to the surface-parallel edge restraint (SS4 boundary condition). The normalized response of [0/90] spherical panels also, as expected, progressively increases with the R/a ratio, reaching more or less its flat plate counterpart, studied earlier by Oktem and Chaudhuri [101].
The fact that both the antisymmetric saddle-shaped thick panels, with the SS4 type boundary condition prescribed at all four edges, exhibit cylindrical panel-like responses is clearly evident from Figure 3 and Figure 4 above. The graphs for spherical panels, in contrast, show that the membrane action due to shell curvature is more pronounced in the thinner panel regime. In the case of very thick spherical panels (a/h ≤ 10), the influence of the membrane action is, to some extent, supplanted by the effect of inter-laminar shear deformation.
Figure 4b shows that the normalized central moments, of the [0/90] spherical thick (a/h = 5) panels, which monotonically decrease with R/a ratio, are higher than their saddle shaped R1(-) and R2(-) counterparts in the entire range of the R/a ratio considered. of the saddle shaped R1(-) type thick panels, which first increases, reaching its peak at R/a = 20, thereafter decreases with R/a ratio. of the saddle shaped R2(-) type thick panels, which monotonically decrease with R/a ratio, is lower than its R1(-) counterpart in the entire range of the R/a ratio considered.
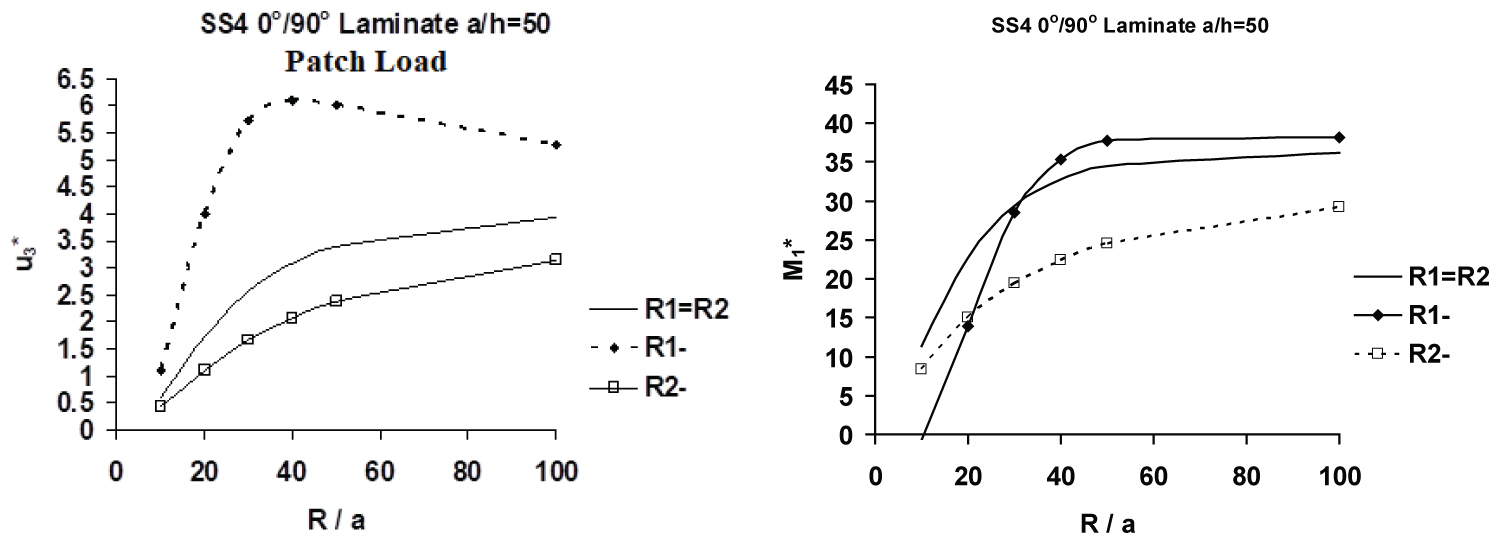
Figure 5a and Figure 5b display variations of normalized central deflections, and moments, , of [0/90] spherical as well as saddle shaped R1(-) and R2 (-) type thin (a/h = 50) panels, with the R/a ratio. It may be noted that in thick [0/90] panels discussed above, the beam-column/tie-bar effects due to (primarily) third order bending-stretching coupling (i.e., Eij's and to a lesser extent, Bij's) has a complex interaction with the membrane action due to curvature, in the presence of full surface-parallel edge restraint (SS4). In [0/90] thinner panels, the beam-column/tie-bar behaviors are similar, albeit less severe, and are primarily caused by the first-order bending-stretching coupling (primarily Bij's), acting either in concert with or in opposition to the membrane action due to the curvature effect. This is a very important factor that should be considered particularly at the initial conceptual design stages of saddle shaped composite panels. Additionally, the normalized deflection of a saddle shaped [0/90] R1(-) type thin panel, like its thick counterpart discussed above, closely resembles that of a thin [0/90] cylindrical panel (R1 = ∞), shown in Figure 9b for a/h = 30 and 50.
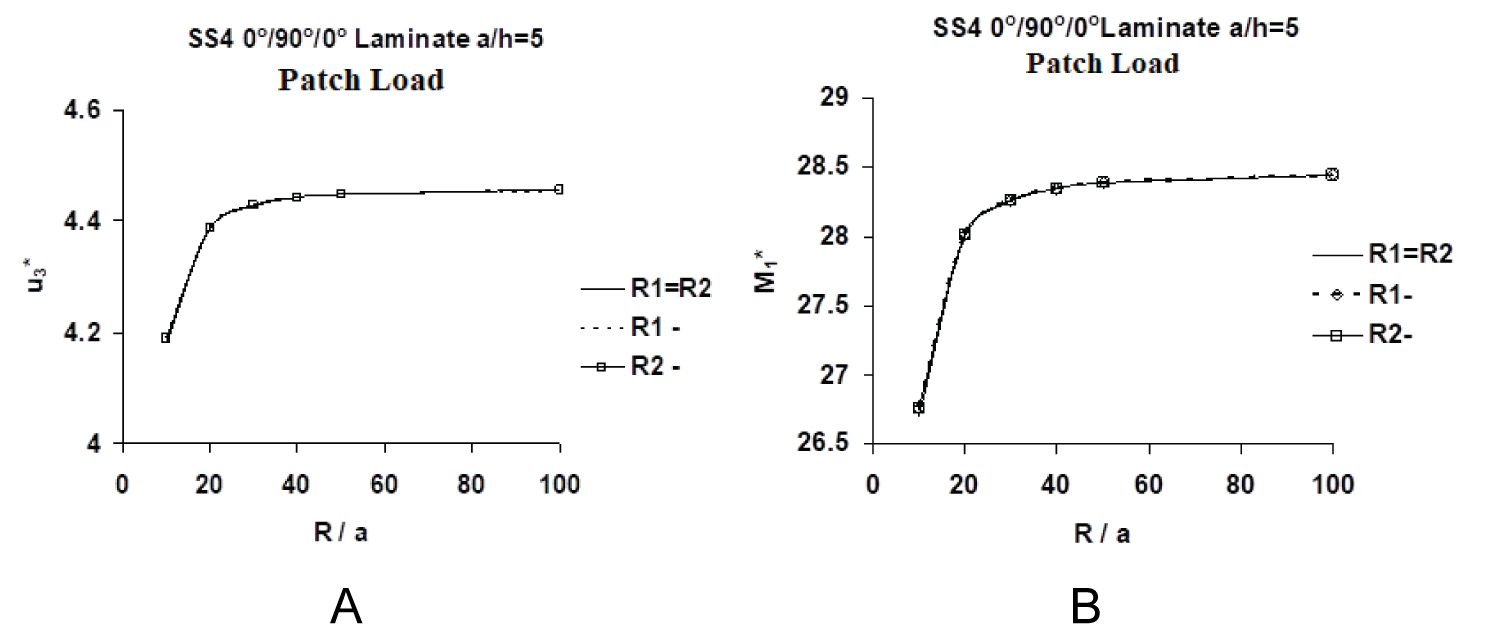
In contrast to the above, as shown in Figure 6a and Figure 6b (respectively, Figure 7a and Figure 7b, the normalized central deflections, , and moments, , of [0/90/0] spherical as well as both type of saddle shaped thick (respectively, thin) panels, are more or less identical, because of absence of any beam-column/tie-bar effect arising out of asymmetry of lamination. Both thick and thin [0/90/0] panels experience lower and in the deeper panel regime, which, as expected, progressively converge to their [0/90/0] plate counterparts [100] in the flatter panel regime.
Figure 6a, Figure 9a, and Figure 9b present the variations of normalized central deflections, of [0/90], [0/90/0] and [0/90/90/0] spherical as well as cylindrical panels, respectively, with the R/a ratio. These plots show that the characteristic of the deflection pattern of a [0/90] curved panel is different from its symmetric ([0/90/0] and [0/90/90/0]) counterparts. Curvature effect (membrane action) is also responsible for the decreased normalized response in both symmetric and antisymmetric type spherical panels for R/a ≤ 20. In Figure 6a, interestingly, the curvature effect increases the normalized deflection of a [0/90] cylindrical panel (R1 = ∞) while it decreases the same of its spherical and cylindrical (R2 = ∞) counterparts. Figure 9a and Figure 9b, however, show that in case of [0/90/0] and [0/90/90/0] spherical as well as cylindrical panels, the behaviors are similar because of absence of any beam-column/tie-bar effects arising out of asymmetry of lamination.
Effects of surface-parallel edge restraints: Comparison between SS1 and SS4 Boundary Conditions
Finally, effects of surface-parallel edge restraints on the response of simply supported moderately deep (R/a = ± R1/a = ∓ R2/a = 10) saddle shaped R1(-) and R2(-) panels under uniform loads are presented in Table 5, Table 6, Table 7 and Table 8. These are quantified by the % difference as given below:
% difference between SS1 and SS4 =
Table 5 portrays the roles played by the beam-column and tie-bar effects arising out of asymmetry of lamination and their three-way interactions with negative Gaussian curvatures as well as surface-parallel edge restraints (or lack thereof), in determining the normalized deflection, , of [0/90] saddle-shaped panels under uniform load. As has been discussed earlier, the saddle shaped panels, R1(-), exhibit greater flexibility (beam-column effect), while the panels, R2(-), display more hardened response (tie-bar effect) in the presence of full surface-parallel edge restraints (SS4 boundary condition). These results provide a clear indication of the beam-column/tie-bar effect, arising out of bending-stretching coupling, in both the R1(-) and R2(-) type panels, which has a complex interaction with the membrane action, caused by the curvature effect, in the presence of surface-parallel edge restraint (SS4 boundary condition). In contrast, both R1(-) type and R2(-) type saddle shaped panels behave more like flat plates, because of the compensating effect of two opposite curvatures in such panels, in the absence of surface-parallel edge restraints (SS1 boundary condition). The three-way interaction of the membrane action due to negative Gaussian curvature with the third order (respectively, first-order) bending-stretching coupling producing a beam- column/tie-bar type softening/hardening effect in a thick (respectively, thin) cross-ply panel and the absence of surface-parallel boundary constraints (represented by the SS1 type simply supported boundary condition) contributes to this flattening effect [98]. This is attested by the closeness of the numerical results to the point of being almost identical presented in the second and fourth columns of Table 5 between themselves as well as to their counterparts presented in the second column of Table 1.
Table 5 further shows that normalized central deflections, , of [0/90] saddle shaped R1(-) panels with full surface-parallel edge restraints (SS4) are higher than their counterparts in the absence of similar edge restraints (SS1) in the thicker panel regime (a/h ≤ 20), as a result of the beam-column effect. The opposite is true in the thinner panel regime, because of the dominance of the membrane action (curvature effect). In contrast, normalized deflections, , of [0/90] saddle shaped R2(-) panels with the SS4 type surface-parallel edge restraints are lower than their SS1 counterparts in the entire range of a/h ratios investigated here, due to the tie-bar effect. Table 6 shows that normalized deflections, , of [0/90/0] saddle shaped R1(-) panels (identical to their R2(-) counterparts) with full surface-parallel edge restraints (SS4) are lower than their SS1 counterparts in the entire range of a/h ratios, because of absence the beam-column/tie-bar effects.
Table 7 shows that normalized central moments, of [0/90] saddle shaped R2(-) panels with full surface-parallel edge restraints are third than their R1(-) counterparts in the entire range of a/h ratios investigated here. Table 7 shows that normalized central moments, of both [0/90] saddle shaped R1(-) and R2(-) panels with full surface-parallel edge restraints (SS4) are third than their counterparts in the absence of similar edge restraints (SS1) in the thicker panel regime (a/h ≤ 20), as a result of the beam-column/tie-bar effects. The opposite is true in the thinner panel regime, because of the dominance of the membrane action (curvature effect), giving rise to even negative values for R1(-) type panels for a/h ≥ 50. In contrast, normalized moments, as shown in Table 6, of [0/90/0] saddle shaped R1(-) panels (identical to their R2(-) counterparts) with full surface-parallel edge restraints (SS4) are lower than their SS1 counterparts in the entire range of a/h ratios, because of absence the beam-column/tie-bar effects.
Comparison with finite element analysis (FEA)
In contrast to its SS1 counterpart, the SS4 boundary condition prescribed on all four edges is more amenable to be reproduced by finite element analysis (FEA). Young's modulus, E, and Poisson's ratio, ν of aluminum are 70 GPa and 0.333, respectively.
SS4 Boundary Conditions for FEA Model are as follows:
At the edges : u2 = 0, and u3 = 0
At edges : u1 = 0, and u3 = 0
All rotations are free. Needless to say, the assumed displacement-based FEM cannot satisfy the natural boundary conditions a priori.
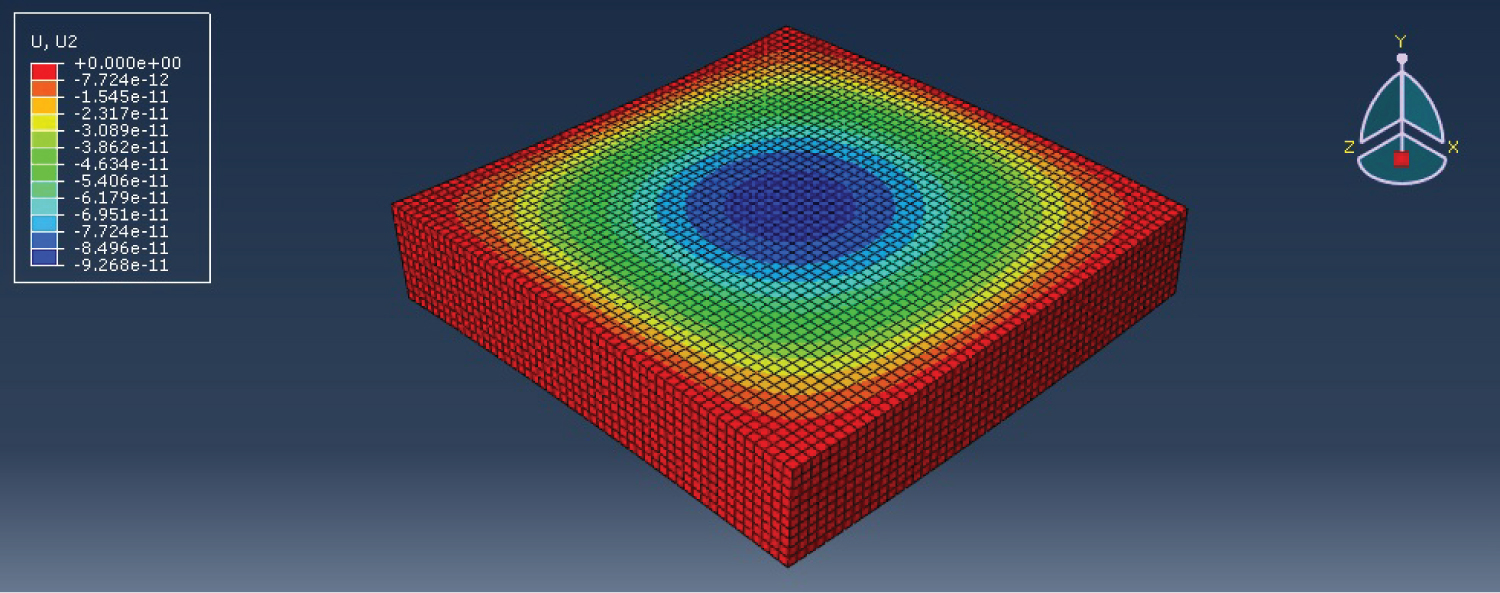
The ABAQUS (version 6.14) solid element, C3D8R, is chosen here because of its similarity to the present TSDT in regard to the transverse shear deformation characteristics. This is an 8-node linear brick element, wherein a reduced integration scheme with hourglass control is implemented. Table 9 shows the ABAQUS convergence results for central deflection of a thick (a/h = 5) moderately deep (R/a = 10) isotropic square (a = b = 1 m) saddle shaped panel under uniform load (q0 = 1 MPa). Figure 7 displays the finite element mesh created using the solid element of ABAQUS. In order to ensure convergence, 9400 elements are used for panels with a/h ratio of 5. Figure 12 displays the deflected shape of an isotropic saddle shaped square thick panel with a/h = 5.
Table 10 and Table11 present comparisons of the central deflections of a thick moderately deep (R/a = 10) saddle shaped isotropic square (a = b = 1 m) panel computed using the SS1 and SS4 solutions, respectively, due to Chaudhuri and Oktem [96,97] with their FEA (ABAQUS Solid Element) counterparts under uniform load (q = 100 MPa). In Table 10 and Table 11, the error or relative difference (RD) is defined as follows:
in which SS1 and SS4 solution is that obtained by Chaudhuri and Oktem [96,97] using a boundary discontinuous double Fourier series approach. Additional details for the SS4 case can be found in Chaudhuri and Oktem [97]. Details relating to the SS1 case are available in Chaudhuri and Oktem [96] and will not be repeated here in the interest of brevity.
As is evident from Table 11, reasonably close agreements between the two sets of solutions are achieved for the SS4 boundary condition. The small differences of 0.64% and 3.52% for a/h = 5 and 10, respectively, can be attributed to the fact that it is not possible to precisely implement boundary discontinuities, such as , , , , arising from the natural boundary conditions relating to the stress couples in the conventional displacement-based finite element schemes, coded in ABAQUS. Only the boundary-discontinuous Fourier analysis of the present type can reproduce precisely the discontinuities in displacement functions and/or their derivatives at the edges. As regards the SS1 boundary condition case shown in Table 10, the larger differences can be attributed to the fact that it is not possible to precisely implement boundary discontinuities, relating to the additional natural boundary conditions relating to the stress resultants, in the conventional displacement-based finite element schemes, coded in ABAQUS. Only the boundary-discontinuous Fourier analysis of the present type can reproduce precisely the discontinuities in displacement functions and/or their derivatives at the edges. Alternatively, a mixed or hybrid type FEA needs to employed for this purpose.
Reliability of the finite element method, based on the assumed displacement potential energy approach, in the neighborhood of stress discontinuities and stress singularities has been discussed by Whitcomb, et al. [111] (at the free edge in a laminated composite), and Chaudhuri [112-120] (at the circumferential corner line of an internal circular cylindrical hole). Whitcomb, et al. [111] have concluded that "the finite element method yielded accurate solutions everywhere except in a region involving the elements closest to the stress discontinuity or singularity and that this region can be made arbitrarily small by refining the finite element model". Chaudhuri [112-114] has probed into the issue much deeper. His conclusion re-affirms, to a rather milder degree, the conclusion reached in the case of its laminate counterpart [115-117] in regards to the accuracy (or lack thereof) of the stresses (more accurately, the stress gradients) computed using the conventional (assumed displacement potential energy based) finite element analysis and computed FEM-based post-processing analysis results for transverse shear stresses in the vicinity of a stress singularity, such as the circumferential corner line of an internal circular/elliptical cylindrical hole.
Summary and Conclusions
A boundary-discontinuous double Fourier series-based solution methodology is employed to solve the problem of a third-order shear deformation theory-based thick cross-ply hyperbolic-paraboloidal panel, characterized by a system of five highly coupled linear partial differential equations, with the SS4-type simply supported boundary condition prescribed at all four edges. For derivation of the complementary solution, the complementary boundary constraints are introduced through boundary discontinuities of some of the particular solution functions and their partial derivatives. Such discontinuities form a set of measure zero. The present solution methodology is based on the fact that the complementary boundary constraints, which are inequalities, play as important a role as the prescribed (admissible) boundary conditions, which are equalities.
The intricacies of the three-way interaction of the SS4 type simply supported boundary condition, which entails action of full surface-parallel edge restraints, with the effect of negative Gaussian curvature have so far remained an enigma in the literature. Novelty of the present approach is thus attested by the ease with which such delicate issues as the cylindricalizing effect of negative Gaussian curvature, in the presence of full surface-parallel restraints at all four edges, on the response of an asymmetrically laminated thick (a/h ≤ 20) cross-ply panel, are tackled using the boundary discontinuous double Fourier series-based methodology. This type of three-way interaction of the membrane action due to negative Gaussian curvature with the third order (respectively, first-order) bending-stretching coupling producing a beam-column (respectively, tie-bar) type softening (respectively, hardening) effect in a thick (respectively, thin) cross-ply panel and the participation of full surface-parallel edge restraints (represented by the SS4 type simply supported boundary condition) conspires to produce the above-mentioned cylindrical panel-like response.
The numerical results computed using the present approach is expected to serve as benchmark solutions to the laminated shell boundary-value problems. Comparison of these results with their spherical counterparts is intended to demonstrate the effect of Gaussian curvature on the deflections and moments of these saddle-shaped panels. The MATLAB code developed herein will provide a handy tool for the early stages of design of the laminated composite panels of negative Gaussian curvature. The key conclusions that emerge from the present numerical results can be summarized as follows:
1. The length-to-thickness ratio, a/h has a significant effect on the computed results. In the thick panel regime (a/h ≤ 20), this is due to the effect of transverse (inter-laminar) shear deformation. [0/90] saddle shaped R1(-) and R2(-) panels as well as their spherical (R1 = R2) counterpart experience steadily decreasing normalized deflections, with increase of a/h. The results for the spherical panel lie in between their two saddle-shaped counterparts, with saddle shaped panel, R1(-), exhibiting greater flexibility (beam-column effect), while the panel, R2(-), displaying more reduced response (tie-bar effect).
2. The curvature effect (membrane action) enhances the normalized deflection of a thick saddle shaped [0/90] R1(-) type panel, which, as has been discussed above, closely resembles that of a [0/90] cylindrical panel (R1 = ∞), wherein stiffening effect of the membrane action is largely compensated by the softening action of the beam-column effect, caused by the bending-stretching coupling rigidities (primarily the higher-order Eij's and to a lesser extent Bij's), acting in concert with the surface-parallel edge restraint (imposed by the SS4 boundary condition).
3. In contrast, the same action decreases the normalized response of its thick saddle shaped [0/90] R2 (-) counterpart, which closely resembles that of a [0/90] cylindrical panel (R2 = ∞), with the game-changer of the stiffening effect of the membrane action now being in synchrony with the hardening action of the tie-bar effect (caused by the bending-stretching coupling rigidities, primarily Eij's and to a lesser extent Bij's), however now acting in opposition to the surface-parallel edge restraint (SS4).
4. In [0/90] thinner panels, the beam-column/tie-bar behaviors are similar, albeit less severe, and are primarily caused by the first order bending-stretching coupling (primarily Bij's), acting either in concert with (R1(-) type panel) or in opposition to (R2(-) type panel) the membrane action due to the curvature effect.
5. The normalized deflection of a saddle shaped [0/90] R1(-) type thin panel, like its thick counterpart discussed above, closely resembles that of a thin [0/90] cylindrical panel (R1 = ∞).
Suggestion for Future Research
First, although the present double Fourier series solutions are confined to general cross-ply thick hyperbolic-paraboloidal panels subjected to SS4 type simply supported boundary condition, the present methodology is general enough to be able to solve arbitrarily laminated panels of negative Gaussian curvature subjected to any combination of admissible boundary conditions. These problems need to be solved in the near future to provide bench-mark analytical solutions for a variety of numerical solutions including those computing using the FEM.
Second, a boundary-value formulation based on trigonometric shear deformation theory [71] for laminated anisotropic panels of negative Gaussian curvature of various ply-orientations, subjected to arbitrary boundary constraints, can also solved using the present approach.
Third and more important, the present and future TSDT-based results for laminated anisotropic panels of negative Gaussian curvature can be compared with their counterparts computed using the zig-zag theory (or layer-wise constant shear angle theory (LCST))-based FEM [4,7,81-89,112-120] in a manner akin to what has been reported in Chaudhuri and Oktem [69].
Fourth, computation of the normalized central deflections by employing both commercial FEA codes (e.g., ABAQUS and ANSYS) and the current MATLAB code based on the boundary continuous double Fourier series, for all parameters, and demonstrating the main differences thus obtained, is an important topic for further research.
Fifth, experimental results are needed to validate the present as well as other higher order shear deformation theory-based models for laminated anisotropic panels of negative Gaussian curvature, in a manner that can be considered as extensions of Refs [90-93,110].
Sixth, isotropic and laminated anisotropic panels of negative Gaussian curvature weakened by through [11,88] and part-through holes, both internal [88,112,113,115,116,118-120] and external [114,117], have not been investigated like their flat and cylindrical panel counterparts. This is an extremely important area for further research.
Seventh, problems relating to the vibration and buckling of isotropic and laminated anisotropic panels of negative Gaussian curvature need to be studied in the same manner as their zero and positive Gaussian curvature counterparts, investigated both analytically [36,40,44,46,48,55-57,62-64] as well as numerically, e.g., FEA [5,12].
Eighth, it is well-known that panels of negative Gaussian curvature perform better in the post-buckling regime, by virtue of their stable post-buckling response ("for sufficiently strong boundary conditions") as well as for being less sensitive to localized initial imperfections such as dents or dimples. However, this entails (both material and geometric) nonlinear analysis, which is beyond the scope of present linear elastic analysis. This said, significant progress has been reported by Kim and Chaudhuri [8,13,17,20,21,24], Hsia and Chaudhuri [14], Chaudhuri and Hsia [15,16], Chaudhuri and Kim [18-20,25-27], Tvergaard and Needleman [23], Chaudhuri [28-32,87,102], Chaudhuri, et al. [33,34], and Chaudhuri and Abu-Arja [104], on large deflection, material nonlinearity, nonlinear resonance (eigenvalue), post-buckling, localization/delocalization, shear crippling type propagating instability, and compression fracture of composite shells/panels of zero and positive Gaussian curvature. In future, we intend to extend such studies to laminated anisotropic panels of negative Gaussian curvature.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Conflicts of Interest/Competing Interests
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Availability of Data and Material
Not applicable.
Code Availability
The code is proprietary; will not be made available at this time.
References
- Ermolenko VM, Kornev VM (1983) Stability of thin shallow shells of negative Gaussian curvature. J Appl Mech Tech Phys 24: 260-262.
- Aksu T (1995) A finite element formulation for shells of negative Gaussian curvature. Computers & Structures 57: 973-979.
- Mau ST, Tong P, Pian THH (1972) Finite element solutions for laminated thick plates. J Compos Mater 6: 304-311.
- Chaudhuri RA, Seide P (1987) Triangular finite element for analysis of thick laminated plates. Int J Numer Methods Eng 24: 1203-1224.
- Kabir HRH, Askar H, Chaudhuri RA (2003) Thermal buckling response of shear-flexible laminated anisotropic plates using a three-node isoparametric element. Composite Structures 59: 173-187.
- Reddy JN (2003) Mechanics of laminated composite plates and shells, theory and practice. (2nd edn), CRC Press.
- Seide P, Chaudhuri RA (1987) Triangular finite element for analysis of thick laminated shells. Int J Numer Methods Eng 24: 1563-1579.
- Kim D, Chaudhuri RA (1995) Full and von Karman geometrically nonlinear analyses of laminated cylindrical panels. AIAA Journal 33: 2173-2181.
- Levyakov SV, Kuznetsov VV (2017) Invariant-based formulation of a triangular finite element for geometrically nonlinear thermal analysis of composite shells. Composite Structures 177: 38-53.
- Chaudhuri RA (1987) A simple and efficient shear-flexible plate bending element. Computers & Structures 25: 817-824.
- Chaudhuri RA, Seide P (1986) Triangular element for analysis of perforated plates under inplane and transverse loads. Computers & Structures 24: 87-95.
- Kim D, Chaudhuri RA (2007) Effect of thickness on buckling of perfect cross-ply rings under external pressure. Composite Structures 81: 525-532.
- Kim D, Chaudhuri RA (2009) Post buckling behavior of symmetrically laminated thin shallow circular arches. Composite Structures 87: 101-108.
- Hsia RL, Chaudhuri RA (1996) Geometrically nonlinear analysis of a cylindrical shell using surface-parallel quadratic elements. Computers & Structures 61: 1143-1154.
- Chaudhuri RA, Hsia RL (1999) Effect of thickness on the large deflection behavior of shells. AIAA Journal 37: 403-405.
- Chaudhuri RA, Hsia RL (1999) Effect of thickness on the large elastic deformation behavior of laminated shells. Composite Structures 44: 117-128.
- Kim D, Chaudhuri RA (2006) Post buckling of moderately thick imperfect rings under external pressure. ASCE J Eng Mech 132: 1273-1276.
- Chaudhuri RA, Kim D (1997) On propagation of shear crippling (kinkband) instability in a long imperfect laminated composite cylindrical shell under external pressure. Int J Solids Struct 34: 3455-3486.
- Chaudhuri RA, Kim D (2003) Localization and shear-crippling instability in a thick imperfect laminated composite ring under hydrostatic pressure. Int J Solids Struct 40: 7063-7092.
- Kim D, Chaudhuri RA (2005) Influence of localized imperfection on the instability of isotropic/cross-ply cylindrical shells/rings under external pressure. Composite Structures 67: 57-70.
- Chaudhuri RA (2008) Effects of fiber misalignment and transverse shear modulus on localization and shear crippling instability in thick imperfect cross-ply rings under external pressure. Composite Structures 82: 587-599.
- Kim D, Chaudhuri RA (2007) Effect of lamination sequence on the localization and shear crippling instability in thick imperfect cross-ply rings under external pressure. Composite Structures 80: 504-513.
- Tvergaard V, Needleman A (2000) Buckling localization in a cylindrical panel under axial compression. W. T. Koiter Commemorative Issue, Int J Solids Struct 37: 6825-6842.
- Kim D, Chaudhuri RA (2005) Localized buckling of a bilinear elastic ring under external pressure. ASCE J Eng Mech 131: 221-224.
- Chaudhuri RA, Kim D (2008) Influence of localized imperfection and surface-parallel shear modulus nonlinearity on the instability of a thin cross-ply cylindrical shell under external pressure. Composite Structures 82: 235-244.
- Chaudhuri RA, Kim D (2009) Effects of thickness and transverse shear modulus nonlinearity on the post-localization response of an imperfect cross-ply ring. Composite Structures 88: 83-96.
- Chaudhuri RA, Kim D (2008) Sensitivity of the post-localization response of a thick cross-ply imperfect ring to transverse Young's modulus nonlinearity. Composite Structures 84: 44-55.
- Chaudhuri RA (2006) Localization, delocalization and compression fracture in moderately thick transversely isotropic rings under external pressure. J Eng Mater Technol 128: 603-610.
- Chaudhuri RA (2015) Effects of thickness and fibre misalignment on compression fracture in cross-ply (very) long cylindrical shells under external pressure. Proceedings of the Royal Society A 20150147.
- Chaudhuri RA (2016) Stress intensity factor and energy release rate of externally pressurized thick cross-ply (very) long cylindrical shells with low-hardening transverse shear modulus nonlinearity. Eng Fract Mech 151: 138-160.
- Chaudhuri RA (2016) Localization, delocalization and compression fracture in externally pressurized thick cross-ply (very) long cylindrical shells with material non-linearity: A multi-scale and multi-physics analysis. Int J Non-Linear Mechanics 84: 68-81.
- Chaudhuri RA (2018) A nonlinear resonance (eigenvalue) approach for computation of elastic collapse pressure of a harmonically imperfect moderately thick ring. Thin-Walled Structures 127: 344-353.
- Chaudhuri RA, Kim D, Pavliga JR (2008) A nonlinear resonance (eigenvalue) approach for computing elastic collapse pressure of a moderately thick cross-ply imperfect ring. Composite Structures 82: 117-126.
- Chaudhuri RA, Pavliga JR, Kim D (2008) Effects of thickness and modal imperfection amplitude on elastic collapse pressure of a cross-ply imperfect ring. Composite Structures 86: 370-384.
- Chaudhuri RA, Balaraman K, Kunukkasseril VX, (1986) Arbitrarily laminated anisotropic cylindrical shells under internal pressure. AIAA Journal 24: 1851-1858.
- Chaudhuri RA, Kabir HRH (2005) Effect of boundary constraint on the frequency response of moderately thick doubly curved cross-ply panels using mixed Fourier solution functions. Journal of Sound and Vibration 283: 263-293.
- Kapania RK (1989) A review on the analysis of laminated shells. ASME J Pressure Vessel Technol 111: 88-96.
- Qatu MS, Asadi E, Wang W (2012) Review of recent literature on static analyses of composite shells: 2000-2010. Open Journal of Composite Materials 2: 61-86.
- Green AE (1944) Double Fourier series and boundary value problems. Proceedings of the Cambridge Philosophical Society 40: 222-228.
- Green AE, Hearmon RFS (1945) The buckling of flat rectangular plywood plates. Philosophical Magazine 36: 659-687.
- Whitney JM (1970) Effect of boundary conditions on the response of laminated composites. J Compos Mater 4: 192-203.
- Whitney JM (1971) Fourier analysis of clamped anisotropic plates. J Appl Mech 38: 530-532.
- Whitney JM, Leissa AW (1970) Analysis of a simply supported laminated anisotropic rectangular plate. AIAA Journal 8: 28-33.
- Kabir HRH, Khaleefi AM, Chaudhuri RA (2001) Free vibration analysis of thin arbitrarily laminated anisotropic plates using boundary-continuous displacement Fourier approach. Composite Structures 53: 469-476.
- Kabir HRH, Chaudhuri RA (1993) A direct Fourier approach for analysis of thin finite-dimensional cylindrical panels. Computers & Structures 46: 279-287.
- Chaudhuri RA, Kabir HRH (1994) Static and dynamic Fourier analysis of finite cross-ply doubly curved panels using classical shallow shell theories. Composite Structures 28: 73-91.
- Chaudhuri RA, Kabir HRH (1993) Boundary-discontinuous Fourier analysis of doubly curved panels using classical shallow shell theories. Int J Eng Sci 31: 1551-1564.
- Chaudhuri RA, Kabir HRH (1992) A boundary-continuous-displacement based Fourier analysis of laminated doubly curved panels using classical shallow shell theories. Int J Eng Sci 30: 1647-1664.
- Chaudhuri RA, Kabir HRH (1993) A boundary discontinuous Fourier solution for clamped transversely isotropic (pyrolytic graphite) Mindlin plates. Int J Solids Struct 30: 287-297.
- Kabir HRH, Chaudhuri RA (1992) Boundary-continuous Fourier solution for clamped mindlin plates. J Eng Mech 118: 1457-1467.
- Chaudhuri RA (1993) Closure to "Boundary continuous fourier solution for clamped mindlin plates" by Humayun R Kabir and Reaz A Chaudhuri (July, 1992, Vol. 118, No. 7). ASCE J Eng Mech 119: 2364-2366.
- Kabir HRH, Chaudhuri RA (1991) A generalized Navier's approach for solution of clamped moderately thick cross-ply plates. Composite Structures 17: 351-366.
- Chaudhuri RA, Kabir HRH (1992) Influence of laminations and boundary conditions on the response of moderately thick cross-ply rectangular plates. Journal of Composite Materials 26: 51-77.
- Chaudhuri RA, Kabir HRH (1992) Fourier analysis of clamped moderately thick arbitrarily laminated plates. AIAA Journal 30: 2796-2798.
- Chaudhuri RA, Kabir HRH (1993) Vibration of clamped moderately thick general cross-ply plates using a generalized Navier's approach. Composite Structures 24: 311-321.
- Chaudhuri RA, Kabir HRH (1994) Effect of boundary constraint on the frequency response of moderately thick flat laminated panels. Composites Engineering 4: 417-428.
- Kabir HRH, Chaudhuri RA (1994) Free Vibration of clamped moderately thick arbitrarily laminated plates using a generalized Navier's approach. J Sound Vib 171: 397-410.
- Chaudhuri RA, Abu-Arja KR (1988) Exact solution of shear-flexible doubly curved anti-symmetric angle-ply shells. Int J Eng Sci 26: 587-604.
- Chaudhuri RA, Abu-Arja KR (1991) Static analysis of moderately thick finite anti-symmetric angle-ply cylindrical panels and shells. Int J Solids Struct 28: 1-15.
- Chaudhuri RA, Kabir HRH (1989) On analytical solutions to boundary-value problems of doubly curved moderately thick orthotropic shells. Int J Eng Sci 27: 1325-1336.
- Chaudhuri RA, Kabir HRH (1993) Sensitivity of the response of moderately thick cross-ply doubly curved panels to lamination and boundary constraint, part-I: theory. Int J Solids Struct 30: 263-272.
- Kabir HRH, Chaudhuri RA (1991) Free vibrations of shear-flexible anti-symmetric angle-ply doubly curved panels. Int J Solids Struct 28: 17-32.
- Kabir HRH, Chaudhuri RA (1994) On Gibbs-phenomenon-free Fourier solution for finite shear-flexible laminated clamped curved panels. Int J Eng Sci 32: 501-520.
- Kabir HRH, Khaleefi AM, Chaudhuri R (2003) Frequency response of a moderately thick anti-symmetric cross-ply cylindrical panel with mixed type of Fourier solution functions. J Sound Vib 259: 809-826.
- Basset AB (1890) On the extension and flexure of cylindrical and spherical thin elastic shells. Philosophical Transactions of the Royal Society of London A 181: 433-480.
- Chaudhuri RA, Kabir RH (1995) Fourier solution to higher-order theory based laminated shell boundary-value problem. AIAA Journal 33: 1681-1688.
- Oktem AS, Chaudhuri RA (2007) Boundary discontinuous Fourier analysis of thick cross-ply clamped plates. Composite Structures 82: 539-548.
- Oktem AS, Chaudhuri RA (2009) Sensitivity of the response of thick doubly curved cross-ply panels to edge clamping. Composite Structures 87: 293-306.
- Chaudhuri RA, Oktem AS (2022) Effects of surface-parallel edge restraints and inter-laminar shear on the responses of doubly curved general cross-ply panels. J Aerosp Eng Mech (in revision).
- Giunta G, Biscani F, Belouettar S, et al. (2011) Hierarchical modelling of doubly curved laminated composite shells under distributed and localized loadings. Composites B 42: 682-691.
- Mantari J L, Oktem AS, Guedes Soares C (2012) A new trigonometric shear deformation theory for isotropic, laminated composite and sandwich plates. Int J Solids Struct 49: 43-53.
- Chaudhuri RA (1989) On boundary-discontinuous double Fourier series solution to a system of completely coupled P.D.E.'s. Int J Eng Sci 27: 1005-1022.
- Chaudhuri RA (2002) On the roles of complementary and admissible boundary constraints in Fourier solutions to boundary-value problems of completely coupled rth order P.D.E.'s. J Sound Vib 251: 261-313.
- Oktem AS, Chaudhuri RA (2007) Levy type analysis of cross-ply plates based on higher-order theory. Composite Structures 78: 243-253.
- Oktem AS, Chaudhuri RA (2007) Fourier solution to a thick Levy type clamped plate problem. Composite Structures 79: 481-492.
- Oktem AS, Chaudhuri RA (2007) Levy type Fourier analysis of thick cross-ply doubly curved panels. Composite Structures 80: 475-488.
- Oktem A S, Chaudhuri RA (2007) Fourier analysis of thick cross-ply Levy type clamped doubly curved panels. Composite Structures 80: 489-503.
- Khdeir AA, Librescu (1988) Analysis of symmetric cross-ply laminated elastic plates using a higher-order theory: part II - buckling and free vibration. Composite Structures 9: 259-277.
- Oktem AS, Chaudhuri RA (2009) Higher-order theory-based boundary-discontinuous Fourier analysis of simply supported thick cross-ply doubly curved panels. Composite Structures 89: 448-458.
- Seide P (1980) An improved approximate theory for the bending of laminated plates. In: Nemat-Nasser S, Mechanics Today 5 Pergamon Press, New York, 451-465.
- Chaudhuri RA (2005) Analysis of laminated shear-flexible angle-ply plates. Composite Structures 67: 71-84.
- Chaudhuri RA (1986) An equilibrium method for prediction of transverse shear stresses in a thick laminated plate. Computers & Structures 23: 139-146.
- Chaudhuri RA, Seide P (1987) An approximate method for prediction of transverse shear stresses in a laminated shell. Inte J Solids Struct 23: 1145-1161.
- Chaudhuri RA, Seide P (1987) An approximate semi-analytical method for prediction of interlaminar shear stresses in an arbitrarily laminated thick plate. Computers & Structures 25: 627-636.
- Chaudhuri RA (1990) On the prediction of interlaminar shear stresses in a thick laminated general shell. Intl J Solids Struct 26: 499-510.
- Carrera E (2003) Historical review of zig-zag theories for multilayered plates and shells. Applied Mechanics Reviews 56: 287-308.
- Chaudhuri RA (2008) A nonlinear zigzag theory for finite element analysis of highly shear-deformable laminated anisotropic shells. Composite Structures 85: 350-359.
- Chaudhuri RA (2009) A new three-dimensional shell theory in general (non-lines of curvature) coordinates for analysis of curved panels weakened by through/part-through holes. Composite Structures 89: 321-332.
- Demasi L (2012) Partially zig zag advanced higher order shear deformation theories based on the generalized unified formulation. Composite Structures 94: 363-375.
- Bert CW, Mayberry BL (1969) Free vibrations of unsymmetrically laminated anisotropic plates with clamped edges. Journal of Composite Materials 3: 283-292.
- Chaudhuri RA, Balaraman K, Kunukkasseril VX (2005) A combined theoretical and experimental investigation on free vibration of thin symmetrically laminated anisotropic plates. Composite Structures 67: 85-97.
- Chaudhuri RA, Balaraman K (2007) A novel method for fabrication of fiber reinforced plastic laminated plates. Composite Structures 77: 160-170.
- Li H, Chang Y, Xu Z, et al. (2018) Modal shape measurement of fiber-reinforced composite plate with high efficiency and precision based on laser linear scanning method. Measurement and Control 51: 470-487.
- Chaudhuri RA, Oktem AS, Guedes Soares C (2015) Levy-type boundary Fourier analysis of thick clamped hyperbolic-paraboloidal cross-ply panels. AIAA Journal 53: 140-149.
- Chaudhuri RA, Oktem AS, Guedes Soares C (2015) Levy-type boundary Fourier analysis of thick cross-ply panels with negative Gaussian curvature. AIAA Journal 53: 2492-2503.
- Chaudhuri RA, Oktem AS (2016) Analysis of simply supported saddle-shaped symmetric cross-ply panels with no surface-parallel boundary constraints. AIAA Journal 54: 782-788.
- Chaudhuri RA, Oktem AS (2016) Simply supported saddle-shaped thick symmetric cross-ply panels: full surface-parallel boundary constraints. AIAA Journal 54: 2194-2199.
- Chaudhuri RA, Oktem AS (2020) Flattening effect of negative Gaussian curvature on simply supported thick asymmetric cross-ply panels in absence of surface-parallel edge restraints. ASCE J of Aerosp Eng 33.
- Jones RM (1999) Mechanics of Composite Materials. (2nd edn), Taylor and Francis.
- Chaudhuri RA (1988) A degenerate triangular shell element with constant cross-sectional warping. Computers & Structures 28: 315-325.
- Oktem AS, Chaudhuri RA (2008) Effect of inplane boundary constraints on the response of thick general (unsymmetric) cross-ply plates. Composite Structures 83: 1-12.
- Chaudhuri RA (2010) A micro-kink theory for determination of shear modulus of a unidirectional composite lamina. Composite Structures 92: 395-400.
- Chaudhuri SN, Chaudhuri RA, Benner RE, et al. (2006) Raman spectroscopy for characterization of interfacial debonds between carbon fibers and polymer matrices. Composite Structures 76: 375-387.
- Chaudhuri RA, Abu-Arja KR (1986) Plastic deformation of a boron/aluminum tube under multi-axial loadings. Computers & Structures 24: 915-921.
- Chaudhuri RA, Oktem AS, Guedes Soares C (2013) Internally pressurized thin cross-ply cantilever cylindrical shells. AIAA Journal 51: 2523-2526.
- Chaudhuri RA, Oktem AS, Guedes Soares C (2015) Beam-column and tie-bar effects in internally pressurized thin arbitrarily laminated cantilever cylindrical shells. J Eng Mech ASCE 141: 04014131.
- Abu-Arja KR, Chaudhuri RA (1989) Influence of transverse shear deformation on the scaling of cross-ply cylindrical shells. J Compos Mater 23: 673-694.
- Abu-Arja KR, Chaudhuri RA (1989) Moderately thick angle-ply cylindrical shells under internal pressure. ASME J Appl Mech 56: 652-657.
- Chaudhuri RA, Abu-Arja KR (1989) Closed-form solutions for arbitrarily laminated anisotropic cylindrical shells (tubes) including shear deformation. AIAA Journal 27: 1597-1605.
- Kunukkasseril VX, Chaudhuri RA, Balaraman K (1975) A method to determine eighteen rigidities of layered anisotropic plates. Fibre Science and Technology 8: 303-318.
- Whitcomb JD, Raju IS, Goree JG (1982) Reliability of the finite element method for calculating free edge stresses in composite laminates. Computers & Structures 15: 23-27.
- Chaudhuri RA (2009) Computation of transverse shear stresses in the vicinity of the circumferential re-entrant corner line of an internal part-through hole weakening an edge-loaded plate. Composite Structures 89: 315-320.
- Chaudhuri RA (2010) Transverse shear stress distribution through thickness near an internal part-through elliptical hole in a stretched plate. Composite Structures 92: 818-825.
- Chaudhuri RA (2015) A combined FEM and three-dimensional asymptotic solution based analysis on stress concentration/intensity around elliptical/circular cylinder shaped surface flaws in stretched plates. Appl Math Model 39: 5341-5353.
- Chaudhuri RA, Seide P (2010) Interlaminar shear stresses around an internal part-through hole in a laminated composite plate. Composite Structures 92: 835-843.
- Chaudhuri RA, Seide P (2011) Interlaminar shear stresses around internal elliptical cylindrical holes weakening edge-loaded cross-ply plates. AIAA journal 49: 1292-1298.
- Chaudhuri RA, Oktem AS, Guedes Soares C (2013) Stress concentration/intensity around elliptical/circular cylinder-shaped surface flaws in cross-ply plates and validity of St. Venant's principle in the presence of interacting singularities. Appl Math Model 37: 1362-1377.
- Chaudhuri RA, Seide P (1986) Triangular element for analysis of a stretched plate weakened by a part-through hole. Computers & Structures 24: 97-105.
- Chaudhuri RA (1987) Stress concentration around a part-through hole weakening a laminated plate. Computers & Structures 27: 601-609.
- Chaudhuri RA (2007) Weakening effects of internal part-through elliptic holes in homogeneous and laminated composite plates. Composite Structures 81: 362-373.
- Hoff NJ, Rehfield LW (1965) Buckling of axially compressed circular cylindrical shells at stresses smaller than the classical critical value. ASME J Appl Mech 32: 542-546.
Corresponding Author
Reaz A Chaudhuri, Department of Materials Science & Engineering, 122 S. Central Campus Dr., Room 304, University of Utah, Salt Lake City, UT 84112-0560, USA, Tel: (801)-550-0661.
Copyright
© 2022 Chaudhuri RA, Oktem AS. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.