A Thorough Study on the Temporal Accuracy of ALE-URANS Solvers with and without Respecting Geometric Conservation Law

Abstract

The importance of satisfying the Geometric Conservation Law (GCL) to maintain second-order temporal accuracy for flow evaluations on dynamic grids are investigated for a Finite Volume Method (FVM)-based dual-time stepping Unsteady Reynolds-Averaged Navier-Stokes (URANS) solver. For a uniform flow and on prescribed grid motions, it is shown that standard first- and second-order Backwards Difference (BDF) approaches for grid velocity assessments do not preserve the uniform flow condition. In addition, except for rigid grid motions, analytic velocity assessment alters the flow uniform state as well. Only the scheme respecting GCL preserves the temporal accuracy of the solver and provides physically meaningful results. This is further confirmed through comprehensive temporal and frequency studies over two periodic flow problems; forced- and natural-laminar vortex shedding behind a 2D flapping plate and a 2D stationary cylinder, respectively. The obtained results emphasize the importance of GCL condition for unsteady flow solvers, which are developed based on Arbitrary-Lagrangian-Eulerian (ALE) formulation.

Keywords

Geometric Conservation Law (GCL), Finite volume method, Temporal accuracy, periodic vortex shedding, 2D Flapping plate, Cylinder flow

Introduction

The importance of respecting the geometric conservation law for unsteady flow problems on dynamic (moving-deforming) grid frameworks has been highlighted in many researches [1-13], after its initial introduction by Thomas and Lombard [14]. According to this law, no disturbance should be introduced by any kind of arbitrary mesh motion on a uniform flow field [15]. Although it has been mathematically proven that a scheme which satisfies GCL condition is at least first order accurate in time, there is no relationship between preserving GCL condition and the temporal accuracy of the solvers on dynamic grids [1,4]. In another word, satisfying GCL condition is not a necessary condition to achieve the temporal accuracy of the underling flow solver, if it is more than first order [4].

It is shown that there is not a unique set of velocities to satisfy GCL condition; instead, a family of functions exists, which may represent the grid motion [4]. Among them, only a fraction preserves temporal accuracy of the flow solvers. More interestingly, it is possible to construct schemes that do not respect GCL condition, but achieve high-order temporal accuracies [1,4]. Nevertheless, numerous performed studies have shown that a scheme which satisfies GCL condition and achieve high-order temporal discretization accuracies on dynamics grids are superior to those that just preserve the temporal accuracy [4].

On the other hand, it has been claimed that if sufficiently small time-steps are selected to advance flow solutions, GCL condition can be violated in practice [2,5,8]. Despite the vast use of this statement that simplifies grid velocity evaluation, difficulties may arise in simulation. It should be noted that the computational costs of unsteady flow solvers strongly depend on the marching time step. Restricting the time steps to small values drastically increases the associated simulation costs, which is not acceptable for many practical industrial applications. In addition, except after conducting expensive temporal studies, there is no rule to assign the maximum allowable time step for these approaches.

In the present study, the effects of satisfying GCL condition on a 2^nd order accurate (temporal and special) flow solver (NSCODE) is investigated [16,21]. Arbitrary Lagrangian-Eulerian (ALE) forms of laminar Navier-Stokes equations are discretized in a Finite-Volume (FVM) framework. Dual-Time Stepping (DTS) approach with a Second-Order Backward Difference Method (BDF2) for evaluation of temporal derivatives is employed in the flow solver to achieve second-order temporal accuracy, while 2^nd order JST scheme [15] is used for spatial flux evaluations. For the pseudo-time iteration, the modified Runge-Kuta scheme, which benefits from local time stepping, implicit residual smoothing, and multi grid approaches as convergence accelerators is employed. Grid velocities are assessed using four methodologies; analytical, GCL-based, and first and second-order backward difference methods, BDF1 and BDF2.

In order to perform a comprehensive study, three test cases are conducted. For the first study, the main characteristic of the GCL, which states any arbitrary grid motion should not alter a uniform flow condition, is investigated. Periodic rigid translation and rotation as well as deforming conditions are imposed and the flow state is assessed after passing a full period. It is shown that only if the GCL requirements are considered the flow remains at its desired original condition. To further highlight the importance of GCL, two periodically unsteady flow problems are investigated. In the first case, unsteady flow around a 2D flapping plate is simulated, where the grid heaves rigidly. Knowing the fundamental forced induced frequency enables an accurate approach for evaluation of mean flow quantities and conduction of a precise temporal and spectral study. For the next case, the natural vortex shedding behind a stationary 2D cylinder is investigated. An arbitrary grid motion is imposed on the grid nodes, where the grid cells are periodically deformed (both in volume and shape) with a frequency that is different from the natural shedding frequency. While in reality the grid motion as well as its motion frequency should not affect the flow characteristic, this would not be exactly reflected in the numerical results. In fact, any numerical approach that does not respect the underlying conservation laws may introduce numerical errors stemming from the included two different frequencies and their interactions. Again an extensive temporal and spectral study showed that the proposed GCL approach preserves the under-lining second-order temporal accuracy of the solver.

Mathematical Modeling

In time-dependent integral form, Navier-Stokes equations are expressed as follow [15],

$$\frac{\partial }{\partial t}{\displaystyle \underset{\Omega }{\int }wd\Omega +{\displaystyle \underset{\partial \Omega }{\int }\left({{\displaystyle F}}_{c\text{}}-{{\displaystyle F}}_{\nu }\right)}}ds\text{ = 0 (1)}$$

Where the state vector ω, in viscid flux vector F_c, and viscous flux vector F_v, are described respectively by

$$\omega \text{ =}\text{}\left\{\begin{array}{l}\rho \\ \rho \mu \\ \rho \nu \\ \rho {\rm E}\end{array}\right\},{{\displaystyle F}}_c\text{ = }\left\{\begin{array}{l}\rho {{\displaystyle V}}_r\\ \rho \mu {{\displaystyle V}}_r\text{ + }{{\displaystyle n}}_{x}p\\ \rho \nu {{\displaystyle V}}_r+{{\displaystyle n}}_{y}p\\ \rho {\rm H}{{\displaystyle V}}_r\text{ + }p{{\displaystyle V}}_t\end{array}\right\},\text{ and }{{\displaystyle F}}_{\nu }\text{ = }\left\{\begin{array}{l}0\\ {{\displaystyle n}}_x{{\displaystyle \tau }}_{xx}\text{ + }{{\displaystyle n}}_y{{\displaystyle \tau }}_{xy}\\ {{\displaystyle n}}_x{{\displaystyle \tau }}_{yx}\text{ + }{{\displaystyle n}}_y{{\displaystyle \tau }}_{yy}\\ {{\displaystyle n}}_x{{\displaystyle \theta }}_x\text{ + }{{\displaystyle n}}_y{{\displaystyle \theta }}_y\end{array}\right\}\text{ (2)}$$

where

$${{\displaystyle \theta }}_x\text{ = }\mu {{\displaystyle \tau }}_{xx}\nu {{\displaystyle \tau }}_{xy}\text{ + k}\frac{\partial T}{\partial x}\text{ and }{{\displaystyle \theta }}_y\text{ = }\mu {{\displaystyle \tau }}_{yx}\text{ + k}\frac{\partial T}{\partial y}\text{ (3)}$$

In these equations, ρ, µ, υ, T, E and H denote the density, the Cartesian velocity components, the temperature, the total energy per unit mass, and the total or stagnation enthalpy, respectively. Based on the ideal gas assumption, pressure is evaluated through the following equation of state,

$$p\text{ = }\left(\gamma \text{ - 1}\right)\left\{\rho E\text{ - }\frac{{\left(\rho \mu \right)}^2\text{ + }{\left(\rho \nu \right)}^2}{2\rho }\right\}\text{ (4)}$$

Moreover, n_x and n_y represents the components of the outward facing unit normal vector of the surface ∂Ω. V_r and V_t are the contravariant velocity relative to the motion of the grid and the contravariant velocity of the face of the control volume and are defined as,

$${{\displaystyle V}}_r\text{ = }V\text{ - }{{\displaystyle V}}_t,whereV\text{ = }{{\displaystyle n}}_{x}u\text{ + }{{\displaystyle n}}_y\upsilon ,\text{ and }{{\displaystyle V}}_t\text{ = }{{\displaystyle n}}_x\frac{\partial x}{\partial t}\text{ +}{{\displaystyle n}}_y\frac{\partial y}{\partial t}\text{ (5)}$$

For the viscous stresses, Newtonian viscous behavior is considered,

$$\begin{array}{l}{\tau }_{xx}\text{ = 2}\mu \frac{\partial u}{\partial x}\text{ + }\lambda \left(\frac{\partial u}{\partial x}\text{ + }\frac{\partial \nu }{\partial y}\right),{\tau }_{yy}\text{ = 2}\mu \frac{\partial \nu }{\partial y}\text{ + }\lambda \left(\frac{\partial u}{\partial x}\text{ + }\frac{\partial \nu }{\partial y}\right),\\ \text{ and }{\tau }_{xy}\text{ = }\lambda \left(\frac{\partial u}{\partial y}\text{ + }\frac{\partial \nu }{\partial x}\right)\text{ (6)}\end{array}$$

These equations can be non-dimensionalized and written in integral form for a moving/deforming control volume as follows,

$$\frac{\partial \left(\omega \Omega \right)}{\partial t}\text{ + }{\displaystyle \sum _{\partial \Omega }\left({{\displaystyle F}}_c\text{ - }{{\displaystyle F}}_d\right)}\text{ - }\frac{\sqrt{\gamma }{{\displaystyle M}}_{\infty }}{R{{\displaystyle e}}_{\infty }}{\displaystyle \sum _{\partial \Omega }{{\displaystyle F}}_{\upsilon }}S=\text{ 0 (7)}$$

where, artificial dissipations, F_d, are added to to ensure stability. A finite volume scheme is derived by applying the above equations directly to the control volumes to yield a set of ordinary differential equations of the form,

$$\frac{\partial \left(\omega \Omega \right)}{\partial t}\text{ + R}\left(\omega \right)\text{ = 0 (8)}$$

where Ω is the cell volume, and the residual, R(ω), is evaluated by summing the fluxes through the cell faces. Convective fluxes, F_c are spatially discretized using a second-order cell-centred finite-volume methodology, where artificial dissipation of Jameson-Schmidt-Turkel (JST) [22] are employed as for F_d. To compute the required gradients for evaluation of the viscous fluxes, the Green-Gauss formulation at the cell vertices is employed [15]. For the temporal discretization, a second order backward difference formulation is employed resulting into the following implicit stencil [23],

$${{\displaystyle R}}^{*}\text{ = }\frac{3{{\displaystyle \left(\omega \Omega \right)}}^{\left(n+1\right)}\text{ - 4}{{\displaystyle \left(\omega \Omega \right)}}^n\text{ + }{{\displaystyle \left(\omega \Omega \right)}}^{\left(n-1\right)}}{2\Delta t}\text{ + }{{\displaystyle R}}^{n+1}\text{ = 0 (9)}$$

To solve this nonlinear system of equations for ωⁿ⁺¹, a pseudo-time derivative approach is employed.

$$\frac{\partial \left({{\displaystyle \omega }}^{n+1}\right)}{{{\displaystyle \partial t}}^{*}}\text{ + }{{\displaystyle R}}^{*}\text{ = 0 (10)}$$

Within each real time step, ∆t, a number of inner iterations are performed to update ωⁿ⁺¹ in a way that at the convergence, $\frac{\partial \left({{\displaystyle \omega }}^{n+1}\right)}{{{\displaystyle \partial t}}^{*}}\text{ = 0}$ the original desired equation (Eq. (9)) be obtained. This approach is known as the Dual-Time Stepping approach [23]. For inner loop iterations over the pseudo-time, the modified explicit five-stage Runge-Kutta approach is used [22], where the local time stepping, implicit residual smoothing, and multigrid approaches are implemented to enhance convergence [15].

For a grid motion case, based on equation (5), V_t, or equally, $\frac{\partial x}{\partial t}$ and $\frac{\partial y}{\partial t}$ should be evaluated. This can be obtained using first- or, similar to the main equations, second-order backward difference formulations. For instance for $\frac{\partial x}{\partial t}$, BDF1 and BDF2 formulations are obtained as,

$$BDF1:\frac{\partial x}{\partial t}\text{ = }\frac{{{\displaystyle x}}^{n+1}\text{ - }{{\displaystyle x}}^n}{\Delta t}\text{ and }BDF\text{2: }\frac{\partial x}{\partial t}\text{ = }\frac{3{{\displaystyle x}}^{n+1}\text{ - 4}{{\displaystyle x}}^n\text{ + }{{\displaystyle x}}^{n-1}}{2\Delta t}\text{ (11)}$$

Besides, in case that exact trajectory of the grid motions is known, analytical velocities could be easily obtained. To derive the GCL equation, a uniform flow condition is assumed for system of equations (1). As results, these equations would be simplified to the following single equation

$$\frac{\partial }{\partial t}{\displaystyle {\int }_{\Omega }d\Omega }\text{ + }{\displaystyle \underset{\partial \Omega }{\int }{{\displaystyle V}}_t}\cdot dS\text{ = 0 (12)}$$

This equation is known as Geometric Conservation Law or GCL equation. Since the grid locations are known functions of time, to obtain a self-consistent method, the left hand side of this equation can be evaluated by using a similar second-order temporal discretization approach as the underling flow solver.

$$\frac{3{{\displaystyle \Omega }}^{n+1}\text{ - 4}{{\displaystyle \Omega }}^n\text{ + }{{\displaystyle \Omega }}^{n\text{ - }1}}{2\Delta t}\text{ + }{\displaystyle \sum _{\partial \Omega }{{\displaystyle V}}_t\cdot dS}\text{ = 0 (13)}$$

Therefore, the GCL equation implies that the cell edge velocities should be calculated in such a way that their integration over the control volume surfaces (right hand side of the above equation) equalizes to the pre-known volume changes (left hand side). Total cell volume change can be related to the contribution of each cell edge. In fact, summation of the areas that were swept by each edge during a time step resulted into the final cell volume change. This means that ${{\displaystyle V}}_t\cdot dS$ for each edge is equal to the volume difference that is swept by that edge from time n - 1 to n to n + 1

$$\begin{array}{l}{V}_t\cdot dS\text{ = - }\frac{3{\Omega }^{*n+1}\text{}\text{- 4}{\Omega }^{*n}\text{ + }{\Omega }^{*n\text{ - 1}}}{2\Delta t}\\ \text{ = - }\frac{3\left({\Omega }^{*n+1}\text{ - }{\Omega }^{*n}\right)\text{ - }\left({\Omega }^{*n}\text{ - }{\Omega }^{*n\text{ - 1}}\right)}{2\Delta t}\\ \text{ = - }\frac{3\Delta {\Omega }^{*n+1}}{2\Delta t}\text{ + }\frac{1\Delta {\Omega }^{*}}{2\Delta t}\text{ (14)}\end{array}$$

where, Ω^{*n + 1} is the volume that is swept by the edge from n to n+1, and Ω^*n represents the volume that was swept from n-1 to n. In this study, linear trajectories are considered for grid motion from n - 1 to n to n + 1 locations. Finally, the obtained V_t.dS is directly introduced into Eq. (2) for flux evaluations.

Results and Discussion

Results are presented for three cases, where effects of grid velocity evaluations on the temporal accuracy of the solution are investigated; firstly, for a uniform flow field, secondly, for rigid heaving motion of a flat plate, and lastly for an imposed periodically deforming grid for simulation of natural vortex shedding behind a stationary cylinder. For the latter, the grid motion frequency is not the same as flow natural frequency, which is not known a prior and will be assessed as a part of solution.

Uniform flow

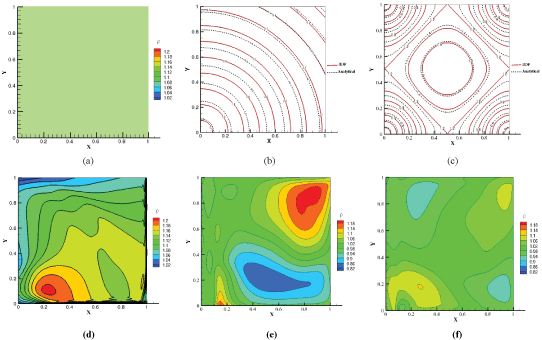
Three different sinusoidal motions are investigated; rigid translation along x and y axes, rigid rotation along the center of coordinate, and a mesh deformation case, in which the cells volume and shape are periodically changed. The status of flow (density contour) is monitored after a completed motion period, when the grid returns back to its original form.

In Table 1, it is illustrated that whether the grid motion alters the uniform flow condition or not. It is clear that that only the approach that satisfy the GCL preserves the flow condition for general motion cases, while analytical method is just applicable for the problems that the grid moves rigidly. Figure 1, presents the density and velocity contours for those cases that failed to satisfy GCL condition (Table 1), as well as fully recovered unaltered density contour for mesh deformation case using GCL approach.

Heaving flat plate

For the second test case, laminar vortex shedding behind a heaving flat plate is studied. Flow and motion parameters are defined as follows,

$$\begin{array}{l}Re\text{ = 800, }M\text{ = 0}\text{.2, }{{\displaystyle f}}^{*}\text{ = 0}\text{.25, }{{\displaystyle y}}^{*}\text{ = 1, }{{\displaystyle \alpha }}_0\text{}\text{= }{{\displaystyle 40}}^0,{{\displaystyle x}}_p^{*}\text{ = 0}\text{.25 (15)}\\ y\text{ = }{{\displaystyle y}}_0\cos \left(2\Pi t\right)\\ \alpha \text{ = }{{\displaystyle \alpha }}_0\sin \left(2\Pi t\right)\end{array}$$

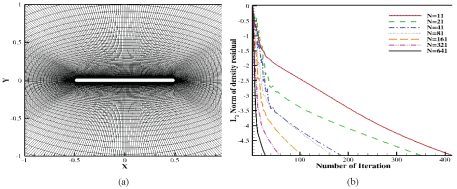
where, ${{\displaystyle f}}^{*}\text{ = }\frac{{{\displaystyle f}}_c}{{{\displaystyle u}}_{\infty }}$ is the reduced frequency, ${{\displaystyle y}}^{*}\text{ = }\frac{y}{c}$ is the normalized heaving amplitude, ${{\displaystyle x}}^{*}\text{ = }\frac{x}{c}$ is the pivot point and c is the chord length. The employed structured grid consists of 6 blocks containing around 50,000 grid points (Figure 2a). Far-field is approximately located at 25 chords, where a far-field vortex correction is applied. No-slip and Riemann invariants boundary conditions are imposed for wall and far-field boundaries, respectively. For a temporal study, the number of time steps per period are seven times refined, where 11, 21, 41, 81, 161, 321, and 641 steps are considered. The criterion for pseudo iteration within each time step is set to fiver-order convergence of L₂ norm for density residual. In Figure 2b, approximate required numbers of pseudo iterations to reach this criterion for different selected time steps are presented. Although increasing number of time steps decreases the number of required pseudo-time iterations, this dependency is not linear. Therefore, the computational costs increase drastically as the number of time steps increases.

In order to perform an accurate temporal study, a convergence criterion should be selected for the real time iterations. Unlike the steady problem where selection of the convergence criterion is straightforward, for unsteady problems this definition is very challenging. Thanks to the fact that this test case converges into a periodic situation after passing the initial transient stage, sinusoidal-based functions may be employed to represent main flow characteristics, like lift and drag coefficients over a period. For instance, lift coefficient is expressed as;

$${{\displaystyle C}}_L\left(t\right)\text{ = }{{\displaystyle a}}_0\text{ + }{\displaystyle \sum _{k=1}^m{{\displaystyle a}}_k\cos \left(k\omega t\right)}\text{ + }{\displaystyle \sum _{k=1}^m{{\displaystyle b}}_k\sin \left(k\omega t\right)}\text{ (16)}$$

where, C_L(t) is the instantaneous lift coefficient, is the averaged lift coefficient over a period, and a_k and b_k are the cosine and sin wave coefficients, respectively. Besides, m is the number of modes in construction of proposed Fourier series over the sampled data. Based on the employed number of time steps in this study (N = 11, 21, 41, 81, 161, 321, and 641), the values for m are 5, 10, 20, 40, 80, 160, and 320, respectively.

For a periodic function, unlike a_k and b_k coefficients, a₀ value does not depend on the period start point. This means that it is possible to perform FFT over the last N obtained data while simulation progresses and monitor convergence of a₀ as the convergence criterion.

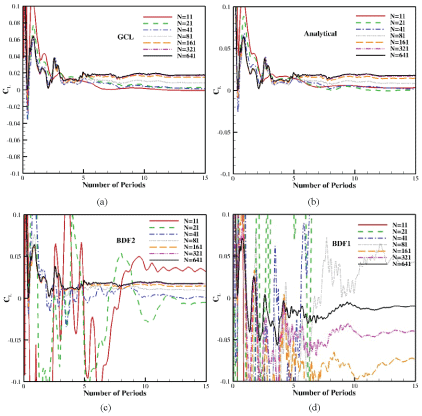
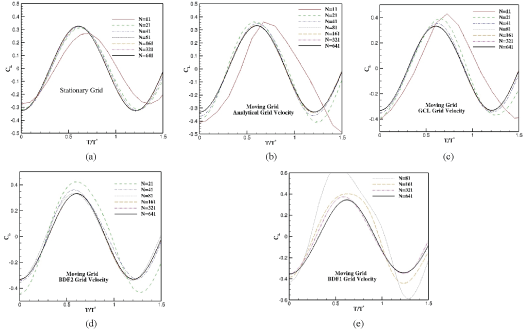
This procedure is followed and the results are presented in Figure 3. From this figure, it is observed that for the studied rigid grid motion, GCL and analytical velocity calculations provide approximately similar results. In addition, around 15 periods were needed to pass the initial transient stage and achieve into a converged average lift coefficient up to 4 significant digits. For BDF2 case, while a similar convergence pattern is observed for cases that have fine time steps (N = 161, 321, 641), deviations happen if the number of steps per period are decreased. Especially, in case of N = 11 and N = 21, errors are higher than usual engineering accuracy requirements. Besides, unlike GCL and analytical cases, more periods should be taken to reach the converged solution. For instance, for 4 significant digits and N = 11 approximately 30 periods are needed. If the grid velocities are evaluated using a first order BDF approach, the results would not be appropriately accurate even for the finest simulated case (N = 641). In addition, cases with N = 11 and N = 21 diverged after large and non-physical oscillations initiated in the far-field.

In Figure 4, instantaneous density contours are presented at the fully periodic state, where 41 time steps are employed for discretization of each period. It is clearly observed that evaluation of grid velocities using GCL approach resulted into an almost identical solution comparing to analytical velocity assessments. This similarity is vanished in case of BDF2, although results are acceptable. In case of BDF1, the results are completely wrong as density non-physically goes up to 2 in far-field cells.

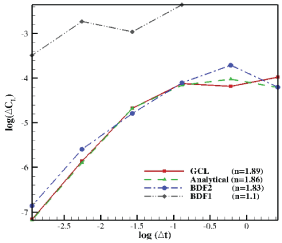
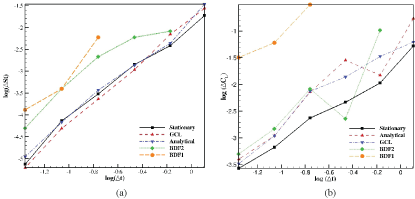
To assess the temporal order of accuracy for the performed simulations, the converged results of the averaged lift coefficients (Figure 2) are used. For the error assessments, results of the finest case (N = 641) are selected as the exact solutions. The obtained data are summarized in Figure 5. This figure highlights that the temporal convergence of GCL and analytical grid velocity assessments follows a similar pattern, where the underlined second-order temporal accuracy (1.89 for GCL and 1.86 for Analytical) is achieved after using 81 time-steps per period. For BDF2, the second order convergence was achieved if the number of time steps is more than 161. Additionally, for N = 11 and N = 21, results are not physically acceptable. For BDF1 approach, the temporal accuracy is dropped to first order. Besides, the error level is much higher comparing to other approaches that may not be acceptable even in case of having very fine time steps.

Cylinder flow

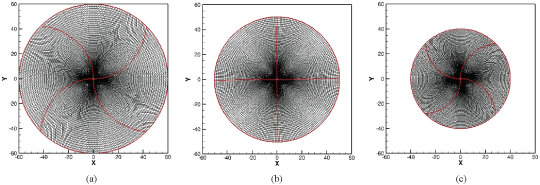
For the third test case, natural laminar vortex shedding behind a stationary cylinder at Re = 100 and M = 0.3 is studied. Unlike the previous case, where the flow shedding frequency was the same as plate motion frequency, here, the natural shedding behavior is not known in advance and should be assessed as solution converges. Nevertheless, in order to conduct a temporal study, time steps (∆t) are selected based on an appropriate initial assumption for shedding period. For the laminar vortex shedding, Strouhal number is roughly around 0.15 [24,25]. Based on this initial assumption, and using 11, 21, 41, 81, 161, 321, and 641 time-steps per period, a similar frequency and temporal study is conducted. Again, the criterion for pseudo-time iterations within each time step is set to fiver-order convergence of L₂ norm for density residual. The temporal study was accompanied for 5 different situations. In the first case, the grid is stationary with no movement. This would be assumed as the base-line case. To monitor the effect of grid movement and the corresponding different velocity assessment methods on possible perturbations in the flow status of the base-line case, an arbitrary but periodic grid motion is imposed, where the grid cells are largely deformed both in volume and shape. The imposed grid motion frequency is based on St = 0.2 to assess possible interactions between grid motion and the flow natural shedding frequencies. In Figure 6, three snap-shots of the grid at their extreme situations during a period cycle is presented. The employed structured grid (256 × 128) is decomposed into 4 blocks. Far-field is approximately located at 40-60 chords, where a far-field vortex correction is applied. Again, no-slip and Riemann invariants boundary conditions are imposed for wall and far-field boundaries, respectively.

Selection of the employed numerical grid was based on a thorough performed grid study on four consecutive grid resolutions (32 × 64, 64 × 128, 128 × 256 and 256 ×512) on the three extreme stationary topologies (Figure 6). Selection of an appropriately fine grid is necessary in order to exclude any spatial discretization error; hence, in the desired performed modal study, only temporal discretization errors present. For the grid study, to exclude the temporal discretization errors, the finest time step (n = 641) has been selected. The obtained data (Table 2) resulted into the selection of 128 × 256 grid for the temporal study. The negligible discrepancy in the converged results between the three selected extreme meshes (Figure 1) is due to high level of grid skewness.

Knowing the exact motion trajectory of grid points enables to analytically evaluate their velocities at desired temporal steps throughout a period. In addition to the analytical velocities, BDF1 and BDF2 approaches as well as GCL method are conducted. All the data are presented after passing the initial transient part and reaching fully developed periodic flow condition.

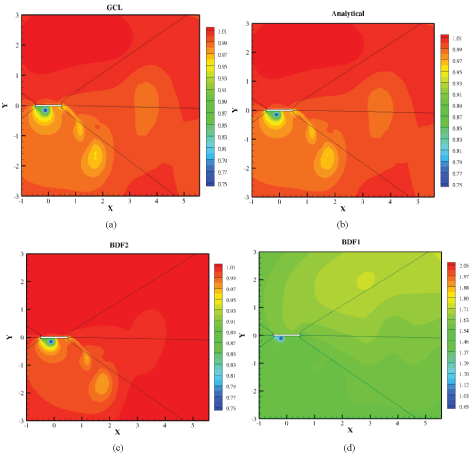
In Figure 7, the temporal evolution of lift coefficients over the initially guessed period (based on St = 0.15) are presented for all the studied cases. Comparing Figure 7b and Figure 7c, where analytical and GCL approach are followed for grid motion assessments with the base-line case, Figure 7a, where the grid is stationary illustrates that for lower time steps (N = 11 and N = 21), slight deviations are observed, while this discrepancy diminished for finer time steps. For BDF2, the case with N = 11 time steps diverged after a few time steps. In a worse situation for BDF1, N = 11, 21, and 41 did not resulted into a converged solution and code stability was only achieved after using at least 81 time steps per period. Besides, even for finest time step (N = 641), notable difference between the obtained lift coefficient curve and base-line case is observed.

In Table 3, the obtained Strouhal number and maximum lift coefficients are presented for all performed numerical studies. Again, from this table it is clear that the base-line results for stationary grid are appropriately reproduced by analytical and GCL approaches, while BDF2 and BDF1 methods shows notable deviations.

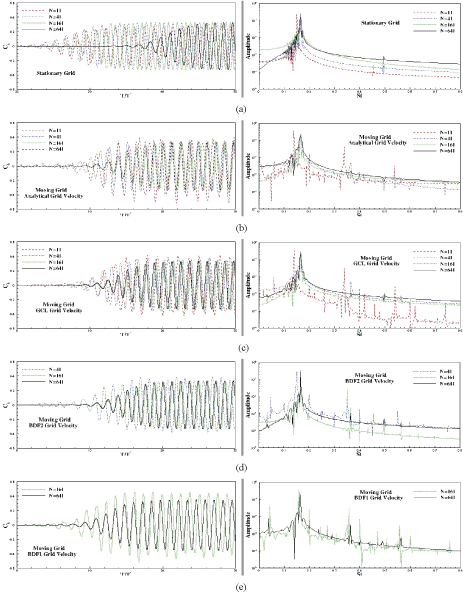
In Figure 8, the temporal evolutions of lift coefficients align with their modal spectrums are presented for all studied cases. From Figure 8a, it is clear that a fully periodic flow is obtained with a St ≈ 0.17. In addition to this main frequency, its third harmonic, St = 3 × 0.17 = 0.51 seems to be important. From the rest of figures, it is clearly observed that in addition to the main fundamental frequency and its third harmonic, extra frequencies, which are not physically desired but are introduced due to grid motions, exist. For analytical and GCL approaches, despite having notable noises in the spectrum of the wave with n = 11 time steps, the base-line spectrums are almost recovered as the number of time steps increases. However, this is not the case for BDF2 and BDF1 approaches as notable level of noises remain even in case of the finest temporal studies. This shows a clear interaction between grid motion frequency, St = 0.2, and the flow natural frequency St = 0.17. For instance, in Figure 8d and Figure 8e, spectrum peaks at St = 0.17, St = 0.2, St = 0.2 + 0.17 etc.

To assess the temporal order of accuracy for the performed simulations, the obtained Strouhal number (Figure 9a) and maximum lift coefficients (Figure 9b) are employed. For the error assessments, results of the finest case (N = 641) are selected as the exact solutions. From this figure, it is clearly observed that GCL and analytical velocity assessments follow a very similar pattern as the base-line stationary case, where an almost second order temporal accuracy is achieved. For BDF2, although at the finest levels, second order temporal accuracy is resulted, the level of error and the number of required time steps to be in the second-order asymptotic region is higher. For BDF1, not only stability problems arise for many cases, but also not an appropriate convergence and accuracy levels are observed for even finest temporal studies.

Conclusion

Comprehensive temporal studies over a number of unsteady problems on deformable grid basis disclose that except for very fine time steps, using backward difference schemes for grid velocity assessments destroys the underling solver temporal accuracy and may even results into non-physical solutions. Both analytical and GCL-based velocity assessments provide appropriate and approximately similar results, where selecting large time steps do not result into instability or non-physical flow situations for the far-field cells. Therefore, the restriction of selecting very fine time steps for BDF2 and BDF1 approaches does not exist for GCL and analytical velocity assessments. Considering the excessive computational costs by restriction to very fine time steps, employment of BDF approaches for the grid velocity assessments would be discarded. Besides, non-availability of analytical velocities for general deforming cases highlights more the importance of velocity evaluations based on the GCL equation.

Acknowledgement

The present study was funded by a collaborative R & D Grant No. 41825 with Ecole de Technologie Superior/Bombardier Aerospace/Thales Canada/NRC-IAR/CRIAQ and NSERC.

References

1. Mavriplis DJ, Yang Z (2005) Achieving higher-order time accuracy for dynamic unstructured mesh fluid flow simulations: role of the GCL. 17^th AIAA Computational Flow Dynamics Conference, Toronto, Canada, 2: 1226-1241.
2. Koobus B, Farhat C (1999) Second-order time-accurate and geometrically conservative implicit schemes for flow computations on unstructured dynamic meshes. Computer Methods in Applied Mechanics and Engineering 170: 103-129.
3. Étienne S, Garon A, Pelletier D (2009) Perspective on the geometric conservation law and finite element methods for ALE simulations of incompressible flow. Journal of Computational Physics 228: 2313-2333.
4. Geuzaine P, Grandmont C, Farhat C (2003) Design and analysis of ALE schemes with provable second-order time-accuracy for inviscid and viscous flow simulations. Journal of Computational Physics 191: 206-227.
5. Guillard H, Farhat C (2000) On the significance of the geometric conservation law for flow computations on moving meshes. Computer Methods in Applied Mechanics and Engineering 190: 1467-1482.
6. Förster Ch, Wall WA, Ramm E (2006) On the geometric conservation law in transient flow calculations on deforming domains. International Journal for Numerical Methods in Fluids 50: 1369-1379.
7. Brogniez S, Rajasekharan A, Farhat C (2012) Provably stable and time‐accurate extensions of Runge–Kutta schemes for CFD computations on moving grids. International Journal for Numerical Methods in Fluids 69: 1249-1270.
8. Farhat C, Geuzaine P, Grandmont C (2001) The discrete geometric conservation law and the nonlinear stability of ALE schemes for the solution of flow problems on moving grids. Journal of Computational Physics 174: 669-694.
9. Thomas P, Lombard CK (1979) Geometric conservation law and its application to flow computations on moving grids. AIAA Journal 17: 1030-1037.
10. Blazek J (2005) Computational Fluid Dynamics: Principles and Applications. (2^nd edn), Elsevier.
11. Mosahebi A, Laurendeau E (2015) Convergence characteristics of fully and loosely coupled numerical approaches for transition models. AIAA Journal 53: 1399-1404.
12. Hasanzadeh K, Laurendeau E, Paraschivoiu I (2013) Validation and verification of multi-steps icing calculation using CANICE2D-NS code. AIAA Paper.
13. Jameson A, Schmidt W, Turkel E (1981) Numerical solutions of the euler equations by finite volume methods using Runge-Kutta time-stepping schemes. AIAA paper.
14. Jameson A (1991) Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings. AIAA paper.
15. Mosahebi A Nadarajah S (2012) Dynamic mesh deformation for implicit adaptive non-linear frequency domain method. Seventh International Conference on Computational Fluid Dynamics (ICCFD7).
16. Williamson CHK (1989) Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J Fluid Mech 206: 579-627.