Critically Evaluating Mechanics of Structure Genome-Based Micromechanics Approach

Abstract

The objective of this paper is to critically evaluate the accuracy and efficiency of a general-purpose micromechanics approach based on the Mechanics of Structure Genome (MSG), when it is applied to the constitutive modeling of 3D structures. The Generalized Method of Cell (GMC) is chosen as a reference method during efficiency evaluation. The predictions by Three-Dimensional Finite Element Analysis (3D FEA) are chosen as benchmarks during accuracy evaluation. Composites such as a continuous fiber-reinforced composite, a particle-reinforced composite, two discontinuous fiber-reinforced composites, and a woven composite are analyzed using MSG, GMC, and 3D FEA. During homogenization, MSG is found to be as accurate but much more efficient than 3D FEA, and despite high efficiency, GMC is found to sacrifice accuracy for efficiency. During dehomogenization, MSG is found to be as accurate as 3D FEA, but GMC is found not to be so accurate. The fidelity of MSG, when it is applied to the modeling of other structures (e.g., beams, plates, and shells), can be similarly evaluated.

Keywords

Homogenization, Dehomogenization, Effective properties, Local fields, Accuracy, Efficiency

Introduction

In recent decades, composites are increasingly used in engineering applications due to their capability of exhibiting high strength-to-weight ratio, improved thermal conductivity, improved permittivity, or even negative Poisson's ratio. Their wide use leads to an increasing need for accurately and efficiently achieving their effective properties. This, however, is challenging because: first, it is often difficult or expensive to measure these effective properties; second, the scales of macroscopic structures are usually several orders of magnitude greater than those of heterogeneities, making it computationally prohibitive to capture all micro structural details. Therefore, it is of great practical value to analyze composites using a multi scale approach.

According to Yu & Tang [1], a typical micromechanics approach consists of the following steps:

1. Investigate the microstructure of a composite and identify the periodically (at least locally) repeating Unit Cell (UC) or Representative Volume Element (RVE);

2. Compute the effective properties of the composite from the constitutive modeling of the UC, or to say, homogenize the composite;

3. Assign the effective properties to the macroscopic structure to determine the global response;

4. Substitute the global response into the UC and recover the local (displacement, strain, and stress) fields, or to say, dehomogenize the composite.

Various micromechanics approaches have been developed to predict the effective properties. The Voigt-Reuss hypothesis leads to the earliest rules-of-mixtures approaches. Hill [2] demonstrated that the Voigt-Reuss hypothesis could provide rigorous upper and lower bounds of the effective properties of a composite. However, for a real composite, the difference between these two bounds is often too huge to be used in practice. There are two major strategies of overcoming this drawback, i.e., either reducing this difference or obtaining some approximations between the lower and the upper bounds. Other micromechanics approaches include the Mean Field Homogenization (MFH) [3], Hashin and Shtrikman's variational approach [4], the third-order bounds [5], the recursive cell method [6], and the Mathematical Homogenization Theories (MHT) [7,8]. Hollister and Kikuchi [9] evaluated the predictive capabilities of these approaches and found that, for periodic or even locally periodic composites, MHT outperformed the others.

Elaborated efforts have been made not only to homogenize but also to dehomogenize composites. Aboudi [10] developed the Method of Cells (MOC) and later the Generalized Method of Cells (GMC) to achieve this goal. GMC involves subdividing a UC into numerous cuboid subcells and approximating the local quantities with their averages over each subcell. A detailed review on MOC and GMC can be found in Aboudi [11]. GMC endows a user with the capability of modeling continuous, discontinuous, woven, and smart (piezo-electo-magnetic) composites. It also provides libraries of nonlinear deformation, damage, failure, and fiber/matrix debonding models, continuous and discontinuous repeating UCs, and material properties. The software suite is available from NASA Glenn [12,13]. Despite advantages, GMC suffers two major drawbacks. First, mesh a UC with a subcell grid introduces considerable domain approximation errors. Note that it is more accurate to mesh a UC with a finite element mesh. Second, approximating the local quantities with averaged values introduces considerable approximation errors. Note that it is more accurate to reproduce the local quantities with shape functions and nodal values. Aboudi [11] developed the High Fidelity Generalized Method of Cells (HFGMC) to incorporate some mechanisms ignored by GMC (e.g., axial-shear coupling). Williams, et al. [14] demonstrated that HFGMC was more accurate yet more computationally costly than GMC.

Recently Yu [15] proposed the Mechanics of Structure Genome (MSG), which is concerned with the constitutive modeling for composites, based on the concept of Structure Genome (SG). Generalized from the concept of RVE, an SG is defined as the smallest mathematical building block of a structure. MSG illustrates a unified approach to constructing the constitutive models for structures such as 3D structures, beams, plates, and shells, over multiple length scales. One of its unique features is that it bridges the micromechanics analysis of a microstructure with the structural analysis of a corresponding macroscopic structure. MSG has been implemented in SwiftComp™, a general-purpose commercial code for multiscale constitutive modeling. SwiftComp can homogenize and dehomogenize a wide variety of periodic, partially periodic, and aperiodic composite structures such as composite laminates, woven composites, sandwich panels, corrugated plates, and many other buildup structures.

The objective of this paper is to critically evaluate the accuracy and efficiency of the general-purpose micromechanics approach based on MSG, when it is applied to 3D structures. GMC is chosen as a reference method during efficiency evaluation. The predictions by 3D FEA are chosen as benchmarks during accuracy evaluation. Composites such as a continuous fiber-reinforced composite, a particle-reinforced composite, two discontinuous fiber-reinforced composites, and a woven composite are analyzed using MSG, GMC, and 3D FEA.

MSG-Based Micromechanics

MSG provides a general-purpose micromechanics theory when it is applied to the constitutive modeling of 3D structures. The term "genome" means that an SG contains all the constitutive information needed to define a structure in the same fashion as a genome containing all the intrinsic information for an organism's growth and development. Although an SG seems to play a role similar to a RVE, they are essentially distinct, even for the structural analysis of 3D bodies. This can be understood by looking into structures made of composites having 1D, 2D, and 3D heterogeneities (Table 1). For a 1D heterogeneity (e.g., a binary composite consisting of two alternating phases), the SG is a line segment consisting of the connecting sub-line segments with each sub-line segment representing each phase; for a 2D heterogeneity (e.g., a unidirectional fiber-reinforced composite), the SG is a 2D domain; for a 3D heterogeneity, the SG is 3D. Clearly, to describe heterogeneity, an SG can have a dimension as low as that of the heterogeneity, while a RVE must have a dimension determined not only by the heterogeneity but also by the type of properties required by structural analysis. For example, for 3D structural analysis requiring 3D properties, the RVE must be 3D [16]. Moreover, traction and displacement boundary conditions, which are indispensable in RVE-based models, are not needed in MSG. Interested readers can refer to Yu [15] for more details on MSG.

MSG is developed based on the principle of minimum information loss which states that a homogenized body can be obtained by minimizing the information loss when constructing the homogenized body out of an original, heterogeneous body. For a linearly elastic material, the information can be the strain energy density. Specifically, the displacement of the original body can be expressed in terms of that of the corresponding homogenized body as

$$u_i\left(x,y\right)=\overline{u_i}\left(x,y\right)+\delta {\chi }_i\text{ (1)}$$

Where u_i denotes the displacements in the original body, ū_i denotes the displacements in the homogenized body, χ_i denotes the difference between ui and ū_i, commonly referred to as the fluctuating functions in micromechanics, and x and y denote the global and the local coordinates, respectively. The strains in the original body can then be obtained as

$${\epsilon }_{ij}\left(x,y\right)=\overline{{\epsilon }_{ij}}\left(x,y\right)+{\chi }_{\left(i,j\right)}\text{ (2)}$$

Where χ_(i,j) denotes the symmetric gradient of χ_i with respect to the local coordinates, and δ is a small parameter with y = x/δ. Note that higher order terms have been neglected using the variational asymptotic method [17]. It is beneficial to define the kinematic variables in homogenized body in terms of those in the original body as

$${\overline{u}}_i=\langle u_i\rangle and{\overline{\epsilon }}_{ij}=\langle {\epsilon }_{ij}\rangle ,(3)$$

Where the angle brackets denotes average over the SG. Eq. (3) leads to the following constraints on the fluctuating functions:

$$\langle {\chi }_i\rangle =0and\langle {\chi }_{(i,j)}\rangle =0.(4)$$

The principle of minimum information loss seeks to minimize the difference between the strain energy of the original body and that of the homogenized body, i.e.,

$$\Pi =\langle \frac{1}{2}{C}_{ijkl}\left[{\overline{\epsilon }}_{ij}+{\chi }_{(i,j)}\right]\left[{\overline{\epsilon }}_{kl}+{\chi }_{(k,l)}\right]\rangle -\frac{1}{2}{C}_{ijkl}^{*}{\overline{\epsilon }}_{ij}{\overline{\epsilon }}_{kl}\text{ (5)}$$

To minimize Π, consider a homogenized body whose $C_{ijkl}^{*}$ and ${\overline{\epsilon }}_{ij}$ are held fixed. χ_i can be obtained by solving variational statement

$$\underset{{\chi }_i}{\min }\langle \frac{1}{2}{C}_{ijkl}{\epsilon }_{ij}{\epsilon }_{kl}\rangle =\underset{{\chi }_i\in Eq.\left(4\right)}{\min }\langle \frac{1}{2}{C}_{ijkl}\left[{\overline{\epsilon }}_{ij}+{\chi }_{(i,j)}\right]\left[{\overline{\epsilon }}_{kl}+{\chi }_{(k,l)}\right]\rangle .(6)$$

Other constraints such periodic or partially periodic requirements can also be incorporated. Eq. (6) can be either analytically or numerically solved. For simple structures such as binary composites and periodically layered composites (Table 1), analytical solutions are achievable. However, for more general cases, one must resort to a finite element code (e.g., SwiftComp) for problem solving.

Once homogenization is completed, one can dehomogenize the composite. Specifically, introduce the following matrix notations to the global stress and strain column matrices, $\overline{\sigma }$ and $\overline{\epsilon }$ :

$$\overline{\sigma }={\lfloor \begin{array}{cccccc}{\overline{\sigma }}_{11}& {\overline{\sigma }}_{22}& {\overline{\sigma }}_{33}& {\overline{\sigma }}_{23}& {\overline{\sigma }}_{13}& {\overline{\sigma }}_{12}\end{array}\rfloor }^T(7)$$

$$\overline{\epsilon }={\lfloor \begin{array}{cccccc}{\overline{\epsilon }}_{11}& {\overline{\epsilon }}_{22}& {\overline{\epsilon }}_{33}& 2{\overline{\epsilon }}_{23}& 2{\overline{\epsilon }}_{13}& 2{\overline{\epsilon }}_{12}\end{array}\rfloor }^T.(8)$$

The global constitutive relations can then be expressed as

$$\overline{\sigma }=\overline{D}\overline{\epsilon },(9)$$

Where $\overline{D}$ denotes the 6 × 6 effective stiffness matrix rather of the composite. $\overline{\sigma }$ and $\overline{\epsilon }$ can be partitioned as

$$\overline{\sigma }=\left\{\begin{array}{c}{\overline{\sigma }}_u\\ {\overline{\sigma }}_k\end{array}\right\}and\overline{\epsilon }=\left\{\begin{array}{c}{\overline{\epsilon }}_k\\ {\overline{\epsilon }}_u\end{array}\right\},(10)$$

respectively, where the subscripts $k$ and $u$ denote the known and unknown components, respectively. Eq. (9) can be rewritten as

$$\left\{\begin{array}{c}{\overline{\sigma }}_u\\ {\overline{\sigma }}_k\end{array}\right\}=\left[\begin{array}{cc}{\overline{D}}_{uk}& {\overline{D}}_{uu}\\ {\overline{D}}_{kk}& {\overline{D}}_{ku}\end{array}\right]\left\{\begin{array}{c}{\overline{\epsilon }}_k\\ {\overline{\epsilon }}_u\end{array}\right\}.(11)$$

Rearranging Eq. (11) gives

$$\left\{\begin{array}{c}{\overline{\sigma }}_u\\ {\overline{\epsilon }}_u\end{array}\right\}=\left[\begin{array}{cc}{\overline{D}}_{uk}-{\overline{D}}_{uu}{\overline{D}}_{ku}^{-1}{\overline{D}}_{kk}& {\overline{D}}_{uu}{\overline{D}}_{ku}^{-1}\\ -{\overline{D}}_{ku}^{-1}{\overline{D}}_{kk}& {\overline{D}}_{ku}^{-1}\end{array}\right]\left\{\begin{array}{c}{\overline{\epsilon }}_k\\ {\overline{\sigma }}_k\end{array}\right\},(12)$$

from which the global response of the SG can be fully determined.

Evaluation of MSG-Based Micromechanics

In this section, the efficiency and accuracy of MSG-based micromechanics analysis approach implemented in SwiftComp are critically evaluated. Micromechanics analysis code MAC/GMC 4.0 (provided by NASA Glenn Research Center) is chosen as a reference method during efficiency evaluation. The predictions by commercial finite element analysis code ANSYS are chosen as benchmarks during accuracy evaluation. For comparison purposes, all simulations were run on the same computer. Composites such as a continuous fiber-reinforced composite, a particle-reinforced composite, two discontinuous fiber-reinforced composites, and a woven composite are analyzed using SwiftComp, GMC, and 3D FEA. In each example, the effective properties of a composite, the computing time of each approach, and the distributions of the local stress are investigated. Meanwhile, SwiftComp along with coarse meshes, say SwiftCompR, is also used to better evaluate the efficiency of MSG.

Continuous fiber-reinforced composite

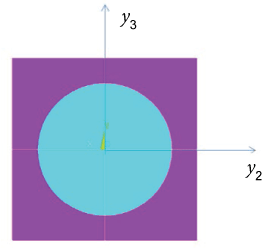
First consider a continuous fiber-reinforced composite consisting of an aluminum matrix and numerous cylindrical, boron continuous fibers arranged in a square array, with a Volume Fraction of Fibers (VOF) of 40%. Let the elastic constants of boron and aluminum take the values listed in Table 2, where E and $\upsilon$ denote Young's modulus and Poisson's ratio, respectively. Let the SG of this composite consist of a square matrix and a circular fiber located at its center (Figure 1). Choose the center of the SG as the origin of the local coordinates, y_i, and the fiber direction and the length and width directions of the SG as the y_1-, the y_2-, and the y_3- directions, respectively.

In SwiftComp, the 2D SG is meshed with 8-node quadrilateral elements having 3 Degrees of Freedom (DOFs) at each node, and the meshed SG consists of 4500 elements. In SwiftCompR, the number of elements is reduced to 320. HFGMC is used only in this example because HFGMC in MAC/GMC 4.0 cannot handle 3D microstructures. In GMC and HFGMC, the 2D SG is meshed with a 66 × 66 subcell grid. In 3D FEA, a 3D SG is needed for complete homogenization, and it is obtained by extruding the 2D SG along the fiber direction. The 3D SG is meshed with 20-node elements (SOLID95), and the meshed SG consists of 4500 elements.

Table 3 lists the predicted effective properties of the composite, by the above approaches. For E₁ and E₂, all predictions are in perfect agreement except that GMC slightly underestimates E2 by 2.02%. For G₁₂ and G₂₃, all predictions are in good agreement except that GMC slightly underestimates G₁₂ and G₂₃ by 6.27% and 4.70%, respectively, and that HFGMC slightly overestimates G₂₃ by 2.10%. Note that, although having a coarse mesh, SwiftCompR still provides perfect predictions.

Table 4 lists the computing time of all approaches. SwiftCompR ran for 0.206 second and is fastest; GMC and SwiftComp ran for 1.34 seconds and 1.70 seconds, respectively, and are also very fast; 3D FEA ran for 168 seconds because it requires a 3D SG; HFGMC ran for 445 seconds, indicating it sacrifices efficiency for accuracy. In summary, when homogenizing the composite, SwiftComp and SwiftCompR are accurate and efficient, and GMC and HFGMC exhibit accuracy-efficiency trade-offs. At last, numerical experiments indicate that, given the same meshed 3D SG, SwiftComp is as accurate but much more efficient than 3D FEA.

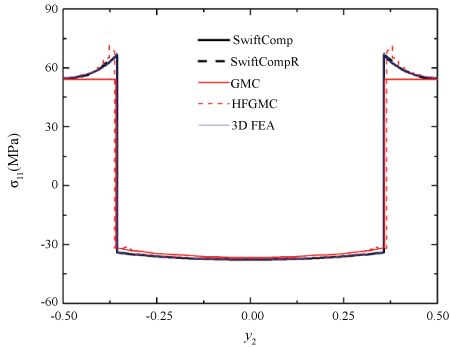
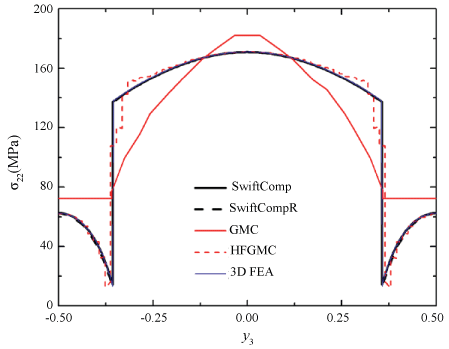
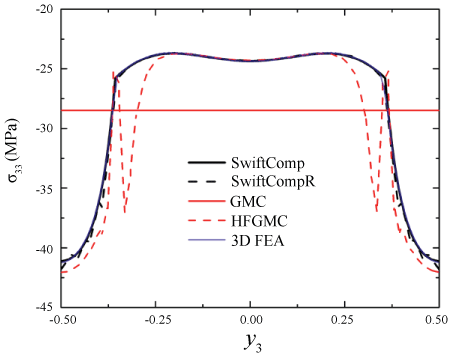
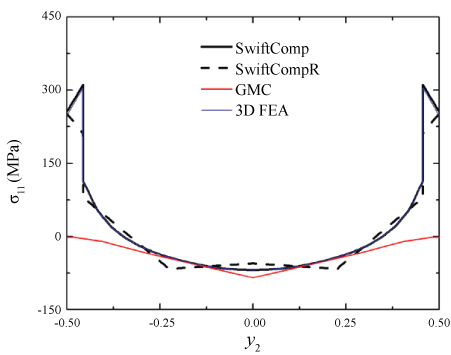
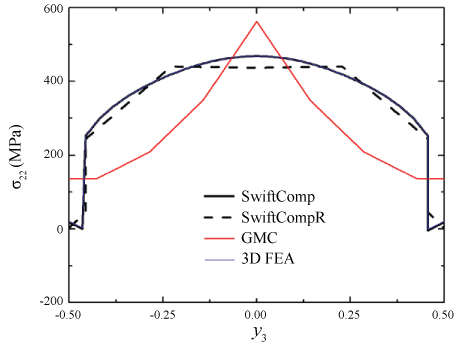
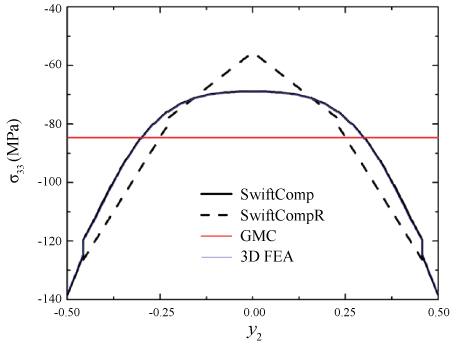
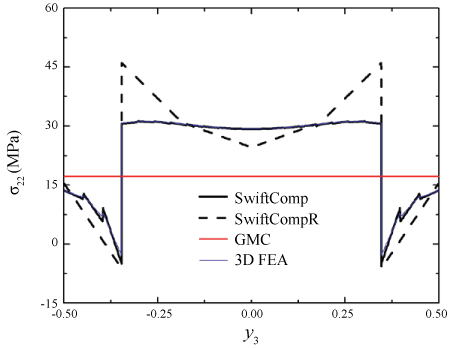
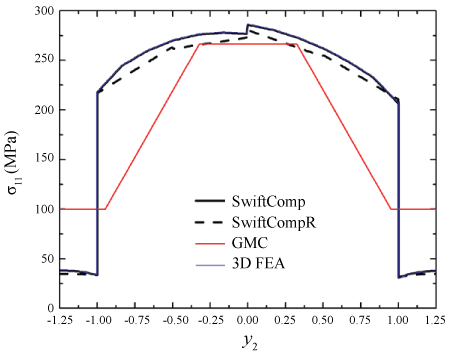
Next let the composite undergo uniaxial extension in the y₂-direction, with ${\overline{\epsilon }}_{22}=0.1\%$. The global response of the SG can be fully determined from Eq. (12), and the local fields can be subsequently recovered. Figure 2 shows the predicted distributions of σ₁₁ along the y₂-axis, by different approaches. All predictions are in good agreement except that the prediction by GMC is underestimated in the matrix. Figure 3 shows the predicted distributions of σ₂₂ along the y₃-axis. The predictions by SwiftComp, SwiftCompR, and 3D FEA are in perfect agreement; the prediction by GMC noticeably deviates from the benchmark in the fiber; the prediction by HFGMC deviates from the benchmark near the fiber/matrix interface. Figure 4 shows the predicted distributions of σ₃₃ along the y₂-axis. The predictions by SwiftComp, SwiftCompR, and 3D FEA are in excellent agreement; the prediction by GMC is even throughout the SG, indicating that GMC cannot effectively predict the distributions of the out-of-plane stresses with a 2D SG; the prediction by HFGMC is accurate near the center of the SG but significantly oscillates near the fiber/matrix interface, indicating that HFGMC sometimes cannot well capture stress discontinuities across interfaces. In summary, Figure 2, Figure 3 and Figure 4 indicate that, when dehomogenizing the composite, SwiftComp and SwiftCompR are as accurate as 3D FEA but only require a 2D SG.

Particle-reinforced composite

Next consider a particle-reinforced composite consisting of an aluminum matrix and numerous spherical boron particles arranged in a cubic array, with a volume fraction of particles of 40%. Let the elastic constants of boron and aluminum take the values listed in Table 2, and let the SG of this composite consist of a cubic matrix and a spherical particle located at its center. Choose the center of the SG as the origin of the local coordinates, y_i, and the length, width, and height directions of the SG as the y₁-, the y₂-, and the y₃-directions, respectively.

In SwiftComp and 3D FEA, the SG is meshed with 20-node elements (SOLID95), and the meshed SG consists of 7776 elements. This finite element model is found to be capable of producing converged results. In SwiftCompR, the number of elements is reduced to 56. In GMC, the SG is chosen to be a built-in spherical particle-reinforced model with 343 subcells.

Table 5 lists the predicted effective properties of the composite, by the above approaches. The predictions by SwiftComp and 3D FEA are in perfect agreement; SwiftCompR accurately predicts G but underestimates E by 0.49%; GMC underestimates E and G by 3.09% and 7.39%, respectively. Table 6 lists the computing time of the above approaches. GMC is slightly faster than SwiftCompR but sacrifices accuracy for efficiency. Meanwhile, Table 5 and Table 6 indicate that, when homogenizing the composite, SwiftComp is as accurate but much more efficient than 3D FEA.

Next let the composite undergo uniaxial extension in the y₂-direction, with ${\overline{\epsilon }}_{22}=0.2\%$. Figure 5 shows the predicted distributions of σ₁₁ along the y₂-axis, by different approaches; Figure 6 the predicted distributions of σ₂₂ along the y₃-axis; Figure 7 the predicted distributions of σ₃₃ along the y₂-axis. The predictions by SwiftComp and 3D FEA are in perfect agreement; the predictions by SwiftCompR deviate from the benchmarks due to the use of a coarse mesh; the predictions by GMC more or less deviate from the benchmarks. Especially for GMC, in Figure 6, the prediction exhibits an erroneous trend, and in Figure 7, the prediction is even throughout the SG. All these indicate that GMC cannot effectively dehomogenize the composite. One possible reason for this is that GMC relies on subcells grid and local quantities even over each subcell and introduces non-negligible approximation errors. Another possible reason is that GMC neglects axial-shear coupling which exists throughout the deformation process of the composite. In summary, Figure 5, Figure 6 and Figure 7 indicate that, when dehomogenizing the composite, SwiftComp is as accurate as 3D FEA.

Discontinuous fiber-reinforced composites

The effective properties of discontinuous fiber-reinforced composites depend not only on VOF but also on the arrangements of discontinuous fibers. To evaluate Swift Comp's capability of handling complex microstructures, consider two discontinuous fiber-reinforced composites with the same VOF: one has its discontinuous fibers arranged in an aligned, transversely regular array, and the other arranged in an aligned, transversely staggered array.

Aligned, transversely regular array

Consider a discontinuous fiber-reinforced composite consisting of a flexible matrix and numerous stiff, cylindrical discontinuous fibers arranged in an aligned, transversely regular array, with a VOF of 40%. Let the elastic constants of the fiber and the matrix take the values listed in Table 7.

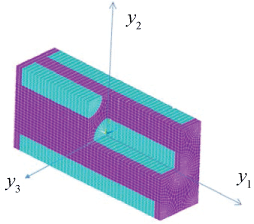
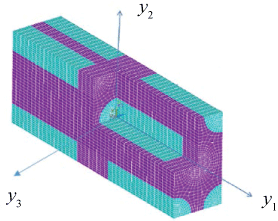
Choose the center of the SG as the origin of the local coordinates, y_i, and the fiber direction and the length and width directions of the SG as the y₁-, the y₂-, and the y₃-directions, respectively. Figure 8 depicts the SG of the composite, which consists of a cuboid matrix, a cylindrical fiber located at its center, and four quarter-cylindrical fibers located at its four edges. Let a and b denote the length and width of the y₂ - y₃ cross section, respectively. Following Pahr & Arnold [18], set $a=\sqrt{3}b$ to make the fiber array hexagonal, and set the fiber aspect ratio (the ratio of the fiber diameter to the fiber length) to be 5. The other dimensions of the SG can be subsequently determined. More details on the SG can be found in Pahr & Arnold [18].

In SwiftComp/3D FEA, a meshed 3D SG is created as follows:

1. Create a meshed area representing the SG geometry on the y₂ - y₃ cross section;

2. Extrude the meshed area along the fiber direction for multiple times to create a series of volumes representing the matrix and the fibers, respectively, and assign corresponding material types to each volume to obtain a 3D SG;

3. Mesh the 3D SG with 20-noded elements (SOLID95).

The meshed SG consists of 28,000 elements (Figure 8). This finite element model is found to be capable of producing converged results. In SwiftCompR, the 3D SG is meshed with 8-noded elements, and the meshed SG consists of 864 elements. In GMC, the 3D SG is meshed with a 3 × 5 × 5 subcell grid. This subcell grid is also found to be capable of producing converged results.

Table 8 lists the predicted effective properties of the composite, by the above approaches. The predictions by SwiftComp and 3D FEA are in perfect agreement; SwiftCompR overestimates E1 by 5.6%; GMC more or less underestimates all effective properties except that it overestimates v₁₂ by 16.35%. Especially, GMC underestimates E₁ and G₂₃ by 24.84% and 21.89%, respectively. Note that, in Pahr & Arnold [18], GMC produced a maximum error of 35%. Therefore, here the errors produced by GMC are in the normal range. Table 9 lists the computing time of the above approaches. GMC is fastest but significantly sacrifices accuracy for efficiency; SwiftCompR is second fastest but is much more accurate than GMC; SwiftComp is as accurate but much more efficient than 3D FEA.

Next let the composite undergo uniaxial extension in the y₂-direction, with ${\overline{\epsilon }}_{22}=0.1\%$. Figure 9 shows the predicted distributions of σ₂₂ along the y₃-axis, by different approaches. The predictions by SwiftComp and 3D FEA are in perfect agreement; the prediction by SwiftCompR noticeably deviates from the benchmark due to the use of a coarse mesh; the prediction by GMC is even throughout the SG, indicating that GMC cannot effectively dehomogenize the composite. Figure 9 indicates that, when dehomogenizing the composite, SwiftComp is as accurate as 3D FEA.

Aligned, transversely staggered array

Next consider a discontinuous fiber-reinforced composite with an aligned, transversely staggered fiber array. Let the SG here be the same as that in the previous example except that: here all quarter-cylindrical fibers are shifted along the fiber direction such that 76% of them overlap the central fiber, in the fiber direction (Figure 10).

In SwiftComp/3D FEA, a meshed3D SG is created similarly to Section 5.3.1. The meshed SG consists of 10,560 elements (Figure 10). This finite element model is found to be capable of producing converged results. In SwiftCompR, the 3D SG is meshed with 20-node elements (SOLID95), and the meshed SG consists of 576 elements. In GMC, the 3D SG is meshed with a 6 × 5 × 5 subcell grid.

Table 10 lists the predicted effective properties of the composite, by the above approaches. The predictions by SwiftComp and 3D FEA are in perfect agreement; SwiftCompR overestimates G₁₂ and G₂₃ by 4.29% and 22.66%, respectively; GMC more or less underestimates all effective properties except v₁₂. Especially, GMC underestimates E₁, E₃, G₁₂ and G₂₃ by 49.30%, 20.19%, 25.34%, and 24.05%, respectively. Table 11 lists the computing time of the above approaches. GMC is still fastest but significantly sacrifices accuracy for efficiency; SwiftCompR remains second fastest but is much more accurate than GMC; SwiftComp is as accurate but much more efficient than 3D FEA.

Next let the composite undergo uniaxial extension in the y₂-direction, with ${\overline{\epsilon }}_{22}=0.1\%$ . Figure 11 shows the predicted distributions of σ₂₂ along the y₁-axis, by different approaches. The predictions by SwiftComp and 3D FEA are in perfect agreement; the prediction by SwiftCompR noticeably deviates from the benchmark due to the use of a coarse mesh; the prediction by GMC exhibits an erroneous trend, indicating that GMC cannot effectively dehomogenize the composite. Figure 11 indicates that, when dehomogenizing the composite, SwiftComp is as accurate as 3D FEA.

Woven composite

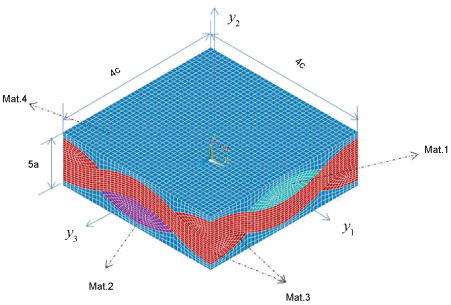
Last consider a woven composite. Figure 12 depicts the SG of the composite. In Figure 12, three materials (Mat. 1-Mat. 3, see Table 12 for their elastic constants and volume ratios) are made into three types of fibers, each of which has an identical elliptical cross section of major axis radius c and minor axis radius c/4; one layer of fabric is woven from these fibers such that each fiber is periodically bent over identical curvature of radius 2.5 c, with the length of periodicity being 4 c; the layer of fabric is then embedded in a matrix (Mat. 4, see Table 12 for its elastic constants and volume ratio) such that the smallest distance between the top surface (or the bottom surface) and one fiber is c/8. The SG turns out to be a cuboid of length 4 c, width 4 c, and height 5 c/4. Choose the center of the SG as the origin of the local coordinates, y_i and the length, height and width directions of the SG as the y₁-, the y₂- and the y₃-directions, respectively.

In SwiftComp and 3D FEA, the SG is meshed with 20-node elements (SOLID95), and the meshed SG consists of 8640 elements. This finite element model is found to be capable of producing converged results. In SwiftCompR, the number of elements is reduced to 576. MAC/GMC 4.0 provides two approaches to homogenizing woven composites, namely single-step GMC and two-step GMC. Here both approaches are used as reference methods. In GMC, the SG is a built-in cuboid model with 64 subcells, while refining the subcell grid does not improve the accuracy.

Table 13 lists the predicted effective properties of the composite, by the above approaches. The predictions by SwiftComp and 3D FEA are in perfect agreement; although having a coarse mesh, SwiftCompR still provides good predictions; single-step GMC and two-step GMC more or less underestimates all effective properties except E2, v₁₂ and v₂₃ and two-step GMC does not noticeably outperform the single-step GMC. Especially, single-step GMC and two-step GMC both under estimates G₁₂ and G13 by 10.08% and 21.65%, respectively, and two-step GMC even overestimates E₂ by 10.70% Table 14 lists the computing time of the above approaches. Single-step GMC is fastest but significantly sacrifices accuracy for efficiency; SwiftCompR is slightly faster and much more accurate than two-step GMC; SwiftComp is as accurate but much more efficient than 3D FEA.

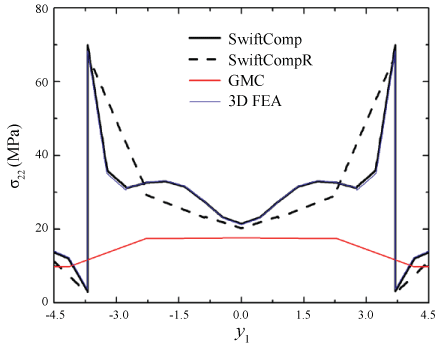
Next let the composite undergo uniaxial extension in the y₁-direction, with ${\overline{\epsilon }}_{11}=0.1\%$. Figure 13 shows the predicted distributions of σ₁₁ along the y₂-axis, by different approaches. Since two-step GMC cannot conveniently dehomogenize composites due to its multilevel homogenization approach, it is not used here. The predictions by SwiftComp and 3D FEA are in perfect agreement; despite the use of a coarse mesh, the prediction by SwiftCompR slightly deviates from the benchmark; the prediction by single-step GMC significantly deviates from the benchmark. Figure 13 indicates that, when dehomogenizing the composite, SwiftComp is as accurate as 3D FEA.

Conclusions

In this paper, the accuracy and efficiency of a MSG-based micromechanics approach is critically evaluated. GMC is chosen as a reference method during efficiency evaluation. The predictions by 3D FEA are chosen as benchmarks during accuracy evaluation. Composites such as a continuous fiber-reinforced composite, a particle-reinforced composite, two discontinuous fiber-reinforced composites, and a woven composite are analyzed using SwiftComp, GMC, and 3D FEA.

The following findings can be obtained from the results:

1. As for homogenization, SwiftComp is as accurate but much more efficient than 3D FEA, not to mention that SwiftComp sometimes only requires a 1D or a 2D SG.

2. SwiftCompR can achieve improved efficiency while ensure satisfactory accuracy.

3. GMC and its variants are very efficient but often sacrifice accuracy for efficiency.

4. As for dehomogenization, SwiftComp is always as accurate as 3D FEA, but GMC and its variants are not, especially when handling complex microstructures.

The following conclusions can be drawn from the above findings:

1. The fidelity of MSG, when it is applied to the modeling of other structures (e.g., beams, plates, and shells), can be similarly evaluated.

2. Given its homogenization capability, MSG can be applied to structural design, analysis, and optimization, as well as uncertainty quantification of composite effective properties.

3. Given its dehomogenization capability, MSG can be applied to the modeling of damage, failure, and interface debonding in composite structures.

Acknowledgements

The authors acknowledge the support of Composite Design and Manufacturing Hub (https://cdmhub.org/) for successful completion of this assessment. The authors also acknowledge NASA Glenn Research Center for the provision of the GMC/MAC 4.0 Code.

References

1. Yu W, Tang T (2007) A variational asymptotic micromechanics model for predicting thermoelastic properties of heterogeneous materials. International Journal of Solids and Structures 44: 7510-7525.
2. Hill R (1952) The elastic behaviour of a crystalline aggregate. Proceedings of the Physical Society Section A 65: 349-354.
3. Hill R (1965) A self-consistent mechanics of composite materials. Journal of the Mechanics and Physics of Solids 13: 213-222.
4. Hashin Z, Shtrikman S (1963) A variational approach to the theory of the elastic behaviour of multiphase materials. Journal of the Mechanics and Physics of Solids 11: 127-140.
5. Milton G (1981) Bounds on the electromagnetic elastic, and other properties of two-component composites. Physical Review Letter 46: 542-545.
6. Banerjee B, Adams DO (2004) On predicting the effective elastic properties of polymer bonded explosives using the recursive cell method. International Journal of Solids and Structures 41: 481-509.
7. Bensoussan A, Lions J, Papanicolaou G (1978) Asymptotic analysis for periodic structures. Amsterdam, North-Holland, Newyork.
8. Murakami H, Toledano A (1990) A high-order mixture homogenization of bi-laminated composites. Journal of Applied Mechanics 57: 388-397.
9. Hollister SJ, Kikuchi N (1992) A comparison of homogenization and standard mechanics analyses for periodic porous composites. Computational Mechanics 10: 73-95.
10. Aboudi J (1986) Elastoplasticity theory for composite materials. Solid Mechanics Archives 11: 141-183.
11. Aboudi J (2004) The generalized method of cells and high-fidelity generalized method of cells micromechanical models-a review. Mechanics of Advanced Materials and Structures 11: 329-366.
12. Bednarcyk BA, Arnold SM (2002) MAC/GMC 4.0 User's Manual Keywords Manual.
13. Bednarcyk B, Arnold S (2002) MAC/GMC 4.0 User's Manual Example Problem Manual.
14. Williams T, Yu W, Aboudi J, et al. (2007) A critical evaluation of the predictive capabilities of various advanced micromechanics models. Proceedings of the 48th Structures, Structural Dynamics, and Materials Conference, Hawaii.
15. Yu W (2016) A unified theory for constitutive modeling of composites. Journal of Mechanics of Materials and Structures 11: 379-411.
16. Sun CT, Vaidya RS (1996) Prediction of composite properties from a representative volume element. Composites Science and Technology 56: 171-179.
17. Berdichevsky V (2009) Variational Principles of Continuum Mechanics. Springer, Berlin.
18. Pahr D, Arnold S (2002) The applicability of the generalized method of cells for analyzing discontinuously reinforced composites. Composite Part B: Engineering 33: 153-170.
19. Massart TJ, Mercatoris BCN, Piezel B, et al. (2011) Multi-scale modelling of heterogeneous shell structures. Computer Assisted Mechanics and Engineering Sciences 18: 53-71.
20. Sevostianov I, Rodriguez-Ramos R, Guinovart-Diaz R, et al. (2012) Connections between different models describing imperfect interfaces in periodic fiber-reinforced composites. International Journal of Solids and Structures 49: 1518-1525.