Optical and Morphological Properties of the Cuticle of Chrysina Resplendens Scarabs: Role of Effective and Structural Pitches

Abstract

Measured reflectance spectra by cuticles of C. resplendens scarabs, in the spectral range 300 to 1000 nm, show high variability depending on the magnitude of the illuminated area, the position of the illuminated section on the elytron of a single specimen, and on the different specimens considered. This fact suggests variability in the depth dependence of the pitch and of the average uric acid concentration, and on the thickness of the retarder layer located between the two helicoidal structures characterizing the cuticle of these beetles. Optical microscopy shows that the surface of the elytron consists of packed scales whose geometrical cross section is about 50 μm². Scanning electron microscopy reveals the morphology of the C. resplendens' cuticle responsible of reflecting circularly polarized light, both left- and right-handed. The dependence with depth through the cuticle is obtained for the effective pitch that characterizes both chiral structures. The relationships between these effective pitches and structural ones are clearly established.

Keywords

Circular polarization, Helicoidal structure, Structural chirality, Reflectance spectra, Effective pitch, Structural pitch

Introduction

The cuticles of Chrysina scarabs have attracted the attention of scientists due to their capacity to circularly polarize their reflected light, besides the striking appearance of these beetles found in tropical cloudy- and/or rainy-forests of the Americas, with the major diversity found in Mexico and in Central America [1-4]. Some research groups focus their efforts on elucidating the mechanisms behind the observed optical behavior of these biological systems, by using ellipsometry techniques [5], spectrophotometric measurements [6], and devised models [7]. It is expected that the knowledge acquired by developing models that interpret the polarizing mechanism will serve as the basis for the development of new functional materials with similar optical properties to those of these cuticles [8-15]. Most Chrysina scarabs considered reflect left-handed circularly polarized light [16]. First reported captures of Chrysina resplendens scarabs were done in Costa Rica at the end of the XIX century [17]. These scarabs reflect both left- and right-handed circularly polarized light, a fact first reported by the laureate physicist Albert Abraham Michelson in 1911 [18,19]. He attributes the presence of both circular polarization components in the reflected light to a screw structure of molecular dimensions through the cuticle of the specimens. The pioneering Caveney's analysis based on electron microscopy reveals the presence of a thick twisted or helicoidal structure of chitin fibrils with left chirality followed by a unidirectional layer and a second thicker left-handed twisted structure in the cuticle of C. resplendens [20].

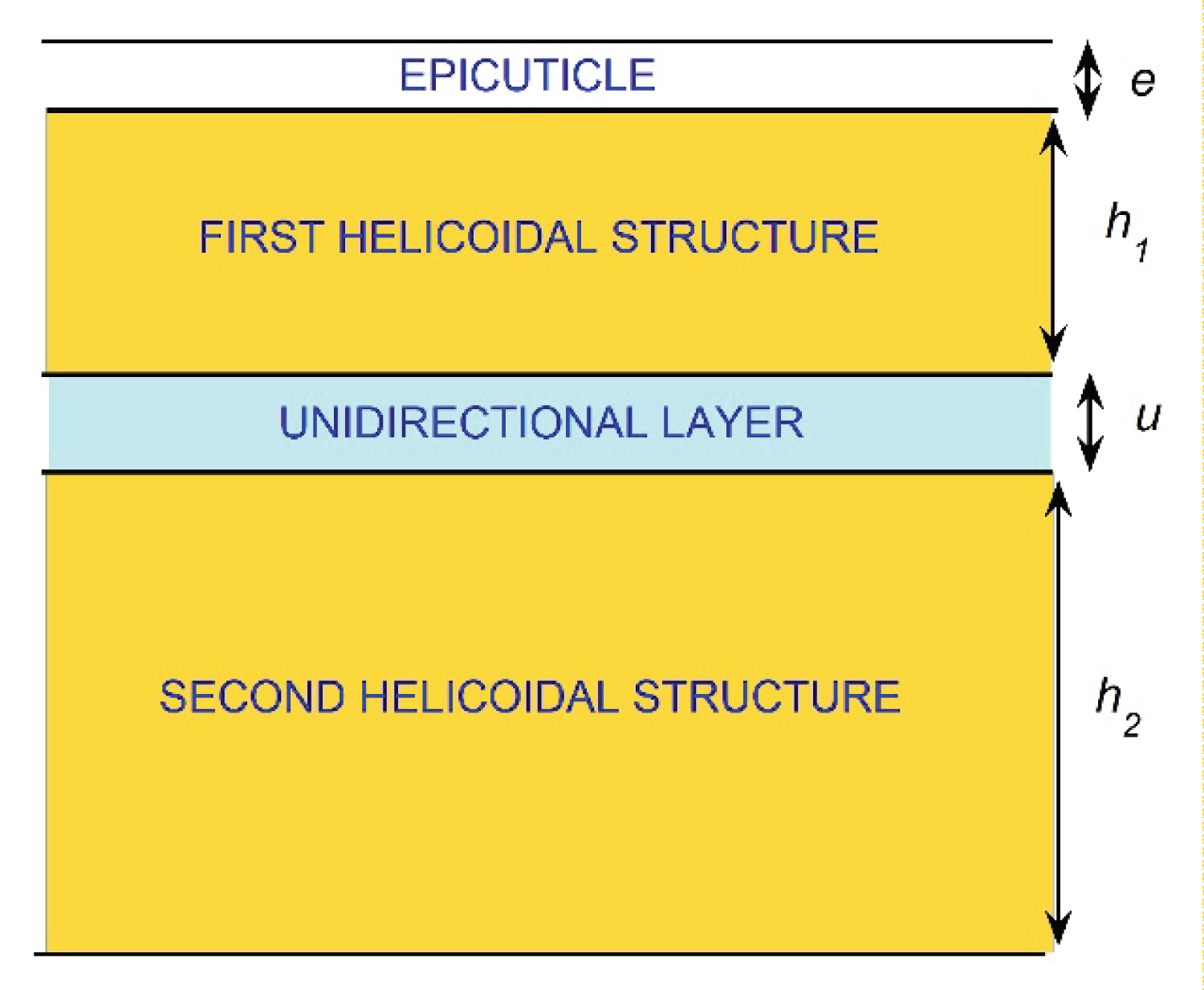
The drawing in Figure 1 schematizes the structure of the cuticle [21]. The left-handed circular polarization (LHCP) component of the incident light is reflected by the first helicoidal structure, with a small contribution of non-polarized light due to the optically homogenous epicuticle coating on top of the exocuticle. The unidirectional layer acts as a half wave plate (HWP) which changes the polarization of the right-handed circular polarized (RHCP) light transmitted through the first left-handed twisted arrangement. LHCP light is transmitted through the unidirectional layer which is reflected by the second helicoidal structure. When this reflected radiation is going back through the unidirectional layer, its polarization state is again changed by the retarder layer, and RHCP light will travel through the first twisted structure emerging as reflected light. Both helicoids behave like photonic crystals for left-handed propagating radiation, whose optical anisotropy is enhanced by the presence of uric acid crystallites embedded in the twisted structures of chitin fibrils. More recently, it has been shown that C. cupreomarginata scarabs also reflect both LHCP and RHCP light [22]. Regarding the C. resplendens, visible spectral photometric measurements are also found in Caveney's work [20] and more recently in the publications of Goldstein [23], McDonald, et al. [24], Finlayson, et al. [25], and Bagge, et al [26]. Visible and near reflectance spectra have been reported by Carter [27]. Extensive ellipsometry studies have also been carried out [28-31]. None of the aforementioned studies systematically documents the variability observed in the reflectance spectra of C. resplendens' cuticles. This is one of the main goals of this article. First, we compare our own measurements with each of them, then they are compared with those carried out by other researchers. These comparisons are not redundant as they show the presence of significant variability in the reflectance spectra. At this level of comparisons, the measurements have been carried out using a single specimen in each study performed. Finally, we use several samples from scarabs captured in the same geographical region, to show that, even within these types of populations, variability in the measured reflectance spectra is present.

In this work we consider the visible and near infrared optical properties of C. resplendens' cuticles in terms of their measured total reflectance spectra, and the LHCP- and RHCP-reflectance. Variability of the measured reflectance spectra, depending on the position of the illuminated area on the elytra, on the size of the illuminated area, and on the specimens considered, is discussed. As a second purpose, the morphology of the chiral structures in the cuticle is considered in terms of effective and structural pitches. The depth-dependent effective pitches of the two cuticle's helicoidal arrangements are obtained from electron microscopy images, and the corresponding structural pitches are reported. The relationship between effective and structural pitches is clearly established for the first time. These topics will be the starting point to consider in a second paper, the modelling of the reflectance spectra, associating the mentioned variability with dispersion on the way the pitches and uric acid concentration depend on depth, and on the thickness of the unidirectional retarder layer.

Visual Appearance, Cuticle's Surface, Optical Measurements, and Internal Morphology

The C. resplendens specimens used in this research work were collected on the slopes of the mountain ranges (MRs) of Costa Rica. Figure 2a shows the physical distribution of the mentioned mountain ranges: The Guanacaste (GMR), the volcanic Central (CMR), and the Talamanca (TMR). Typically, the specimens of C. resplendens are found in altitudes between 800 and 1550 meters above sea level in the GMR and in the CMR. A picture of a C. resplendens scarab, taxonomically identified, is shown in Figure 2b displaying its characteristic and striking visual golden-like appearance. It was captured on the slopes of Tenorio Volcano whose location is indicated by TV in Figure 2a.

As indicated by Boucard [17], its length is about 2.5 cm, and its width is about half its length. When taking a photograph of a specimen, using a filter which transmits LHCP light, the appearance of the beetle is golden (Figure 2c), while with the use of a filter for RHCP light, it shows a less golden appearance with a greenish tonality (Figure 2d). The three-layered system mentioned in the Introduction is covered by a transparent locally flatted layer whose thickness is usually less than one micrometer, the epicuticle or non-chitinous layer [32]. This outer layer really consists of various sublayers characterized by different compositions: The outer one is a cement layer followed by a lipid or waxy layer, a protein layer, a lipo-protein layer, and a basal protein layer at the bottom [33]. From the physical optics point of view, we will consider this structured layer as an effective one denoted as the epicuticle.

Optical Microscopy of the Surface: The Epicuticle

Figure 3a displays a section of a C. resplendens elytron, with an area of about 5.5 × 10⁴ μm² with some fractures through the surface. The picture shows a dark box which illustrates the size of the area to be illuminated by us when measuring reflectance spectra. According to the image shown in Figure 3b, which displays an area of 4.5 × 10³ μm², the waxy epicuticle covering the curved surface of the elytron has a regular texture visually resembling a mosaic or flattened scales which are optically transparent. The geometrical cross section of each scale is about G = 50 μm². We will use this G-value as a reference unit of area with the symbol sc. Due to the high reflectivity of the surfaces of golden- or silver-like Chrysina scarabs, through most of the visible wavelength range, it is difficult to obtain good images of the surface by the use of optical microscopes. As far as we know, it is the first time that the surface of these scale arrangements is reported in golden-like scarabs. More clearly displayed images of the cuticle of other Chrysina green scarabs have been reported in the literature [34,35] and in cholesteric liquid crystals [36].

Given the order of magnitude of the average geometrical cross section of each scale, the corresponding effective average diameter (D) of the observed scales is large when compared to the wavelengths of the illuminating radiation that we have used throughout (λ ε [0.3,1.0] μm), i.e. D = [4G/π]½ = 8.0 μm. As a consequence, significant light scattering by this flatted arrangement of scales is not expected. Additionally, the epicuticle is characterized by low values of its refractive index which means that its contribution to the total reflectance, as specular reflection, is small. This capping layer consists of lipids and waxes whose refractive index (n_w) is between 1.4 and 1.5, and whose main function is to prevent the dehydration of the insect. Hooper, et al. indicate that the refractive index of a waxy layer shows little normal dispersion for visible wavelengths, with values of 1.40 at 543 nm and 1.38 at 633 nm [37]. At normal incidence, specular reflectance values [Rw~(n_w - 1)²/(n_w + 1)²] somewhat lower than 3% are expected by the epicuticle through this visible wavelength range, and the direct transmittance [T_w~4n_w/(n_w + 1)²] will be larger than 97%. Mendoza-Galván, et al. report values of 1.55 at 300 nm and 1.44 at 1000 nm in wavelength for the epicuticle's refractive index [38], which leads to values lower than 5% for the specular reflectance by the epicuticle through this near ultraviolet, visible, and near infrared wavelength range, with a direct light transmittance larger than 95%.

Optical Measurements and Sources of Variability

Total reflectance spectra displayed in Figure 4, when illuminating the cuticle's surface with non-polarized light, were obtained as explained elsewhere [39], through a spectral wavelength range from 300 to 1000 nm. They were measured with an AvaSpec-3648 Fiber-optic spectrometer with a halogen-deuterium lamp (AvaLight DHc), and an aluminum specular reflectance standard (Ocean Optics STAN-SSH) for normalization. Reflectance was measured using a probe made of 6 illuminating fibers around a single light collecting fiber, each of 400 μm in diameter (Avantes reflection probe FCR-7UV400-2-ME). This probe shines on a circular area of approximately 1.3 ± 0.3 mm in diameter when normally placed at 1 mm from the elytron, with an uncertainty in the measurements of around 1%. The illuminated area corresponds to 1.33 × 10⁶ μm² which implies that about 2.65 × 10⁴ sc were illuminated, or at least a large area under which the characteristic helical structure of the cuticle of these beetles would be found, with a certain degree of dispersion as regards to how the effective pitches change with depth beneath the illuminated vertical position. The indirect evidence of this dispersion will be discussed in a progressive way.

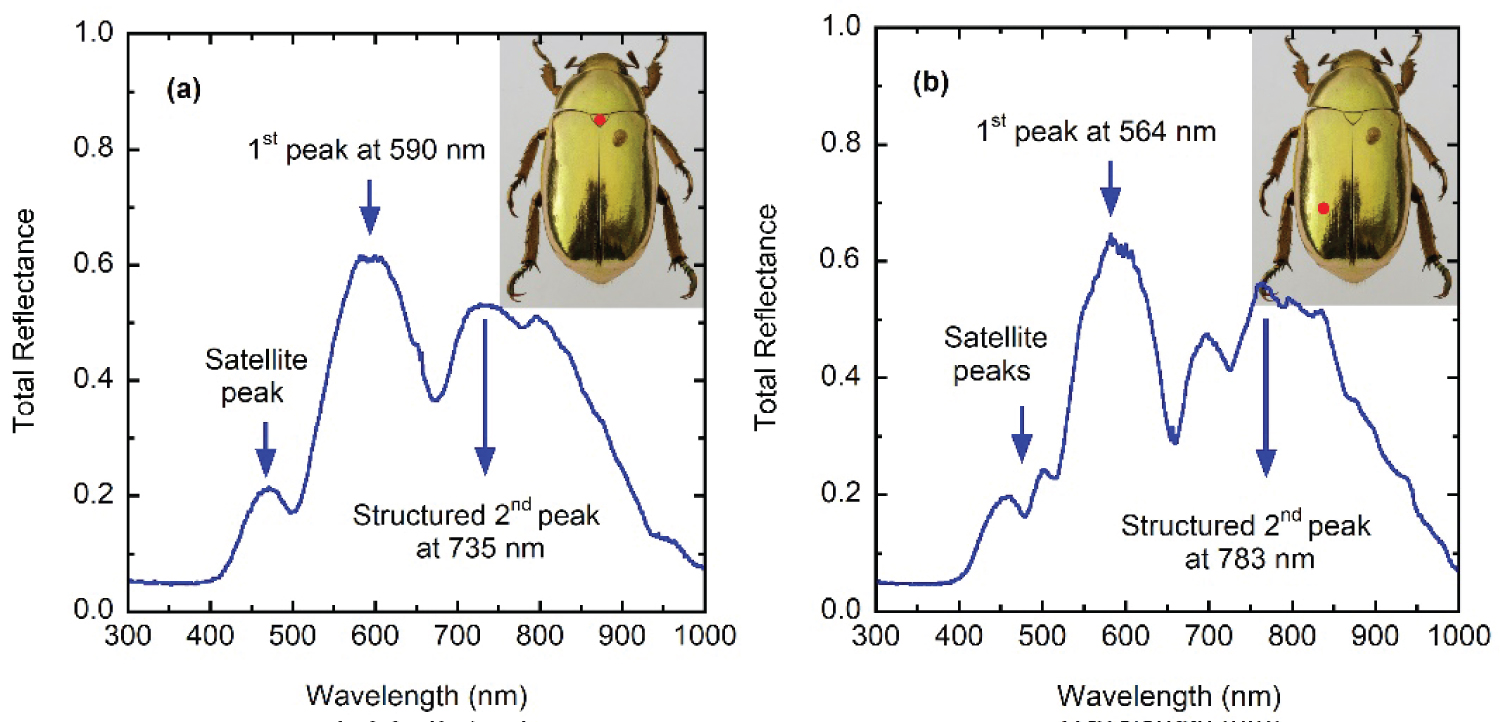
Figure 4 shows total specular reflectance spectra measured at two different sites on the elytron of a specimen. Similar measurements have been reported by Carter through the same spectral range and with a similar illuminated section of the elytron [27]. A position-induced variability is observed when illuminating different sites of the same specimen which can be attributed to some variability in the depth-dependence of the pitch, according to the illuminated site, to variations in the concentration of uric acid crystallites embedded between the chitin micro-fibrils forming the Bouligand twisted structures [40], and/or lateral variations of the unidirectional layer thickness, depending on the illuminated section of the elytron. This variability associated with the position of the illuminated section of the elytron was in fact also observed by Michelson who wrote that the depolarization is only apparent; for on using a moderately high power objective, it is at once evident that there is a structure in the wing-case which causes a difference of phase between the components varying very rapidly from point to point [18]. Ellipsometry measurements have shown this variability in C. gloriosa scarabs [30]. The study of Hegedüs, et al. shows how ellipsometry parameters change with wavelength and position on the curved elytron's surface of Chrysophora chrysochlora and Cetonischema jousselini scarabs [29]. The reflectance spectrum of the scutellum shows two main peaks at 590 and 735 nm (Figure 4a). The first one displays a satellite peak at 470 nm and the second peak shows some irregular spectral structures. The spectrum taken on illuminating the left posterior-lateral section shows the main two peaks at 564 and 783 nm (Figure 3b). The first one shows two satellites peaks at 459 and 500 nm, and the second peak displays a satellite peak at 697 nm. Both main peaks show total reflectance values larger than 50% at their tops, which is indication of having two polarization states in the reflected circularly polarized light. Caveney's work also includes photometric measurements of the reflected light components in a narrower spectral range: From 410 to 670 nm. The LHCP reflected light shows a main peak at 560 nm, with its satellite peak at 457 nm. The RHCP reflected radiation displays a main peak for wavelengths between 575 and 624 nm (Figure 5b in [20]).

In the spectral range 400-700 nm, measurements of McDonald and co authors also show a small satellite peak at short wavelengths with a dominant broad peak through the remaining visible range [24]. The main peak displays a fine structure which is also observed in the measurements carried out by Finlayson, et al. [25], which cover the spectral range 400-850 nm. This ripple structure is probably due to the illumination of a small section of the cuticle corresponding to a spot whose diameter is about 30 μm. In this case, about 14 sc could be exposed to the incident light beam with an expected lower dispersion in the average depth dependence of the pitch, and consequently the reflectance spectra will show a more defined ripple structure as seen in the measurements reported in references [24,25]. The magnitude of the illuminated area introduces an additional surface-induced variability due to the number of effective pitches that could be contributing to an average effective one.

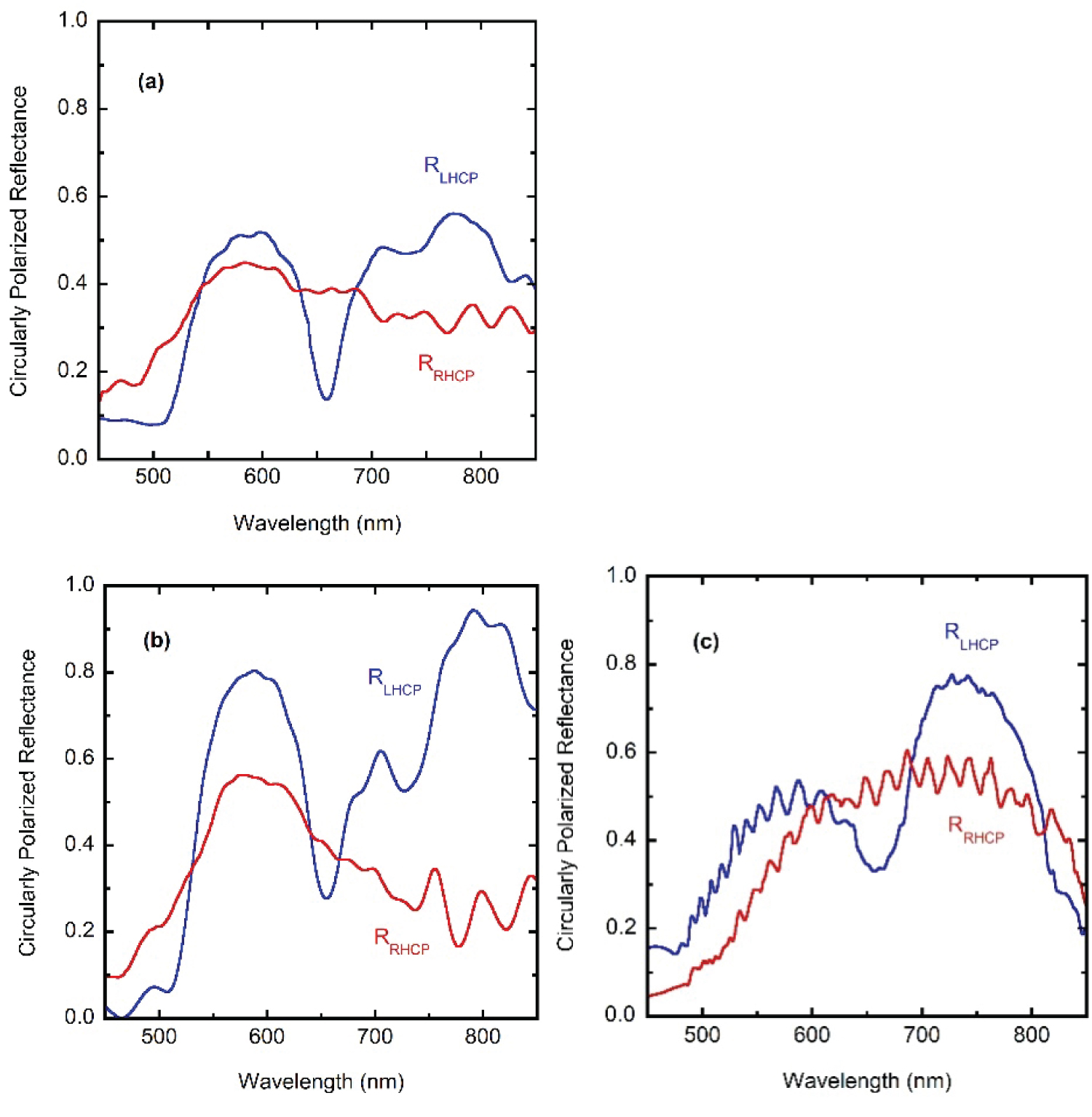
When comparing measurements from different sources, in order to display this additional source of variability in the reflectance spectra, three sets of measurements are depicted in Figure 5, over narrower spectral ranges: (a) R_LHCP and R_RHCP reflectance spectra obtained from the data displayed in Figure 4.18 of [27], which corresponds to an illuminated spot of 2.0 mm in diameter (6.3 × 10⁴ sc), (b) Along with own additional measured spectra illuminating about 200 sc, and (c) R_LHCP and R_RHCP spectra corresponding to Figure 3a in [25], which correspond to illumination of about 15 sc. The evaluations were carried out with the co- and cross-polarized components: R_LHCP = R_LL + R_LR and R_RHCP = R_RR + R_RL. The ripple structure observed in the measurements of Finlayson [25] and McDonald [22] is due not only to the use of a small illumination spot but also to the use of co- and cross-polarized filters. Our second set of reflectance measurements shown in Figure 5b were obtained using a 508 PV UV-Visible-NIR Microscope spectrophotometer (CRAIC, Los Angeles, USA) coupled to an Eclipse LV100 ND Microscope Nikon, Tokyo, Japan). Total reflectance measurements correspond to the average of 10 reflectance spectra from a 100 μm × 100 μm area captured through a 10x magnification objective with an integration time of 160 ms, using a mirror as reflectance standard (STAN-SSH, Ocean Optics, Winter Park, FL, USA). Left- and right-handed circularly polarized light reflectance spectra were measured with the same parameters as total reflectance spectra and on the same illuminated spot but using a left- or right-handed analyzer made of a linear polarizer L-AN analyzer, Nikon, Tokyo, Japan and a quarter wave plate (P-CL ¼ lambda, λ = 546 nm, Nikon, Tokyo, Japan) whose desirable functionality is reliable in the spectral range of 400 to 850 nm. These spectra were normalized subsequently using the reflectance of the mirror through the corresponding analyzer. This procedure allows us to measure all three different spectra on the same spot without moving the sample.

The conclusion is clear: As the number of illuminated sc decreases, the dispersion in the phase differences between rays reflected through the helicoidal structures also decreases and the ripple structure in the reflectance spectra appears with increasing sharpness. The variability of the effective pitch with position on the elytron's curved surface has been shown by McDonald for C. resplendens and other scarabs [22]. From his TEM analysis of the pitch profiles at different sites (see Figure 7.5 in [22]), the variability is not uniform with depth being larger as the depth increases. This fact could explain why the relation between heights of main peaks in the reflectance spectra shown in Figure 5 change when going from illuminating a large section of the cuticle (Figures 5a), to those cases when small sections are illuminated (Figures 5b and Figure 5c).

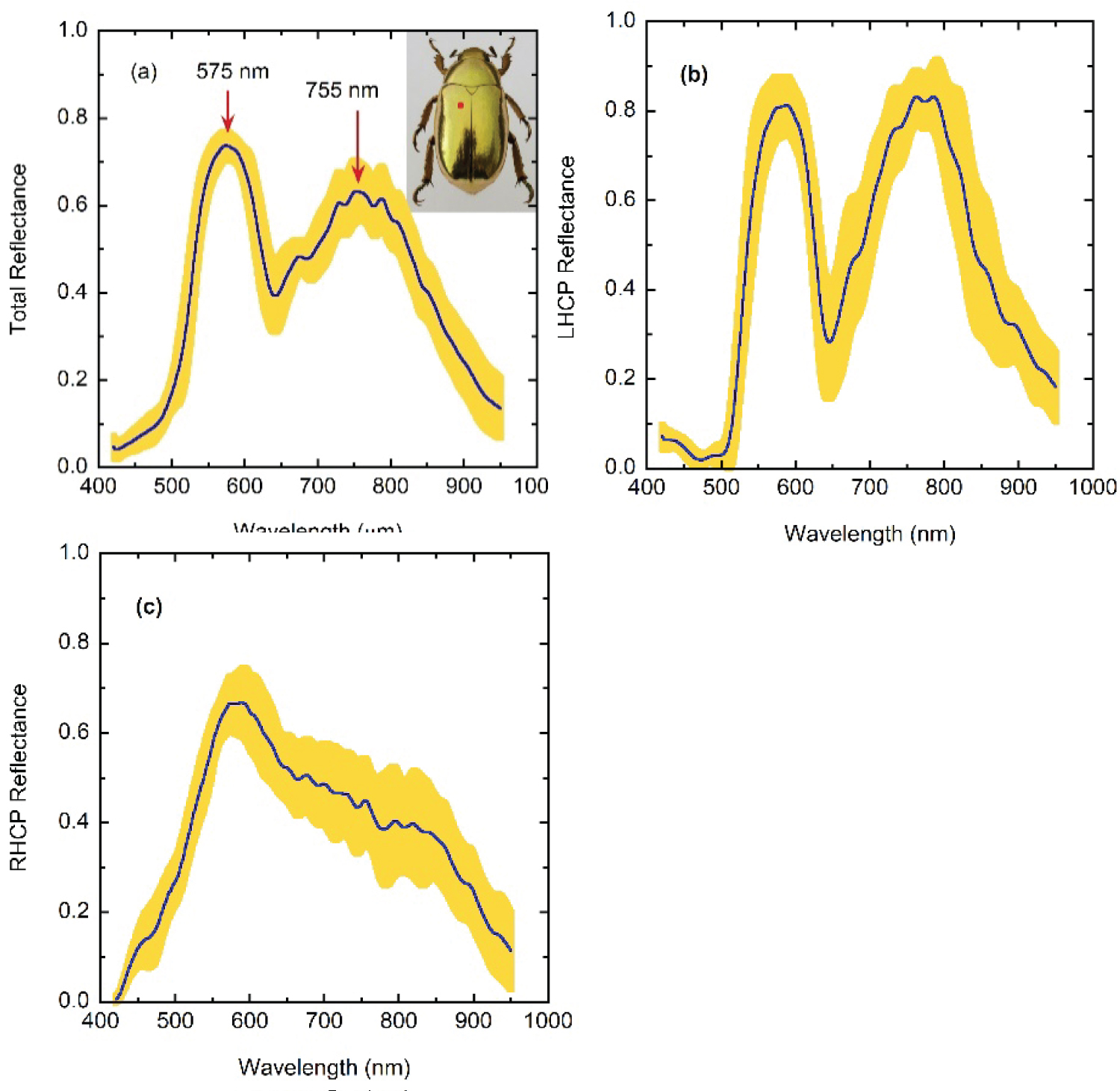
A more extensive set of measurements was carried out by us, the results are summarized in Figure 6 which covers the largest spectral range from the visible to the near infrared. Figure 6a depicts the average total reflectance spectrum [R_T = (R_LHCP + R_RHCP)/2] whose prominent features are two main reflectance peaks at wavelengths of 575 and 755 nm, the second one showing some spectral structure. The width of the reflection band centered at 575 nm is consistent when considering different specimens. The reflectance starts to increase after 500 nm in wavelength. This confers the golden appearance to the cuticle of C. resplendens, the appearance would be silvery for a reflectance edge close to 400 nm. The yellow band about the curve of the spectral mean values of total reflectance indicates the dispersion of the measurements. Its width is obtained by adding and subtracting the standard deviation at each wavelength in measurements taken on 13 different specimens captured in sites of the GMR close to Monteverde Costa Rica, a location near to TV. This is the same geographical region where the specimen shown in Figure 2 was captured. The measurements were carried out by illumination of equivalent sections of the elytra. The red point indicates the section on the dorsal-lateral area where the reflectance spectra were measured. It was chosen for being the flattest section of the elytra.

As seen, significant dispersion is displayed which is probably linked to three mechanisms of variability: Dispersion in the optical-depth dependence of the pitches, in the average volume fraction of uric acid contained in the cuticle, and in the thickness of the retarder layer. The largest dispersions are in the spectral region between reflectance peaks are displayed differences about 20% between minimum and maximum values of reflectance, R_min and R_max respectively, and in the vicinity of the spectral position of the second reflectance peak (differences about 15% between R_min and R_max). The statistical analysis carried out from additional reflectance measurements using the same group of specimens mentioned above indicates that the repeatability of the measurements in the same section of the same specimen is statistically high. There is some fine spectral composition, superimposed on the main features of the average LHCP- and RHCP-reflectance spectra, which is better defined for the LHCP-measurements. This could be interpreted as the presence of a larger variability of the pitch in the second helicoidal structure. The variation when changing the position of the illuminated spot, as mentioned, is high; this fact strongly suggests that the C. resplendens is characterized by significant dispersion on the way that the pitch depends on the depth through each one of the helicoidal structures, on the distribution and average concentration of the uric acid, as well as on the thickness of the unidirectional layer between the two twisted arrangements. The prominent trends observed in each one of the individual reflectance spectra are similar between them: A total reflectance displaying two main reflectance peaks. The spectral average value of the variability is about DR~10% with values between 5 and 10% through the visible, and between 10 and 15% through the near infrared. Figure 6b and Figure 6c displays the decomposition of the total reflectance in terms of its measured left- and right-handed circular polarized components. Somewhat higher variability is displayed by the measurements of the LHCP- and RHCP-reflectance spectra as shown in Figure 6b and Figure 6c, respectively.

The quarter-wave retardation plates commonly supplied with polarizing microscopes are optimized for the visible region and we observe that the measured LHCP-, RHCP-, and total-reflectance curves become increasingly similar in the NIR beyond 850 nm. The blue lines correspond to the averages values which allow to highlight the main spectral features: The LHCP component displays two main peaks with the second one slightly higher than the first, and the RHCP shows a reflection edge close to the mid visible, i.e, a peak around which the reflectance abruptly decreases towards short wavelengths and gradually through larger visible and near infrared wavelengths. The first peak displayed in the total reflectance spectra of Figure 6a, at 575 nm, corresponds to the superposition of a left-handed circularly polarized peak with a right-handed reflectance edge. At this spectral position, the ratio of intensities, γ = R_LHCP/R_RHCP = 1.1 which means that the total reflected light is almost non-polarized. The second peak, close to 755 nm, is mainly due to the reflection of LHCP light with some contribution of RHCP light whose reflectance spectrum depicts a shoulder in the near infrared, γ being equal to about 1.7, i.e., this total reflected light is more elliptically polarized. The corresponding degrees of polarization (DoP) at each peak, which are given by DoP = (R_LHCP - R_RHCP)/(R_LHCP + R_RHCP) = (γ - 1)/(γ + 1), are about 5 and 26%.

Depth-Dependence of the Effective Optical Pitch

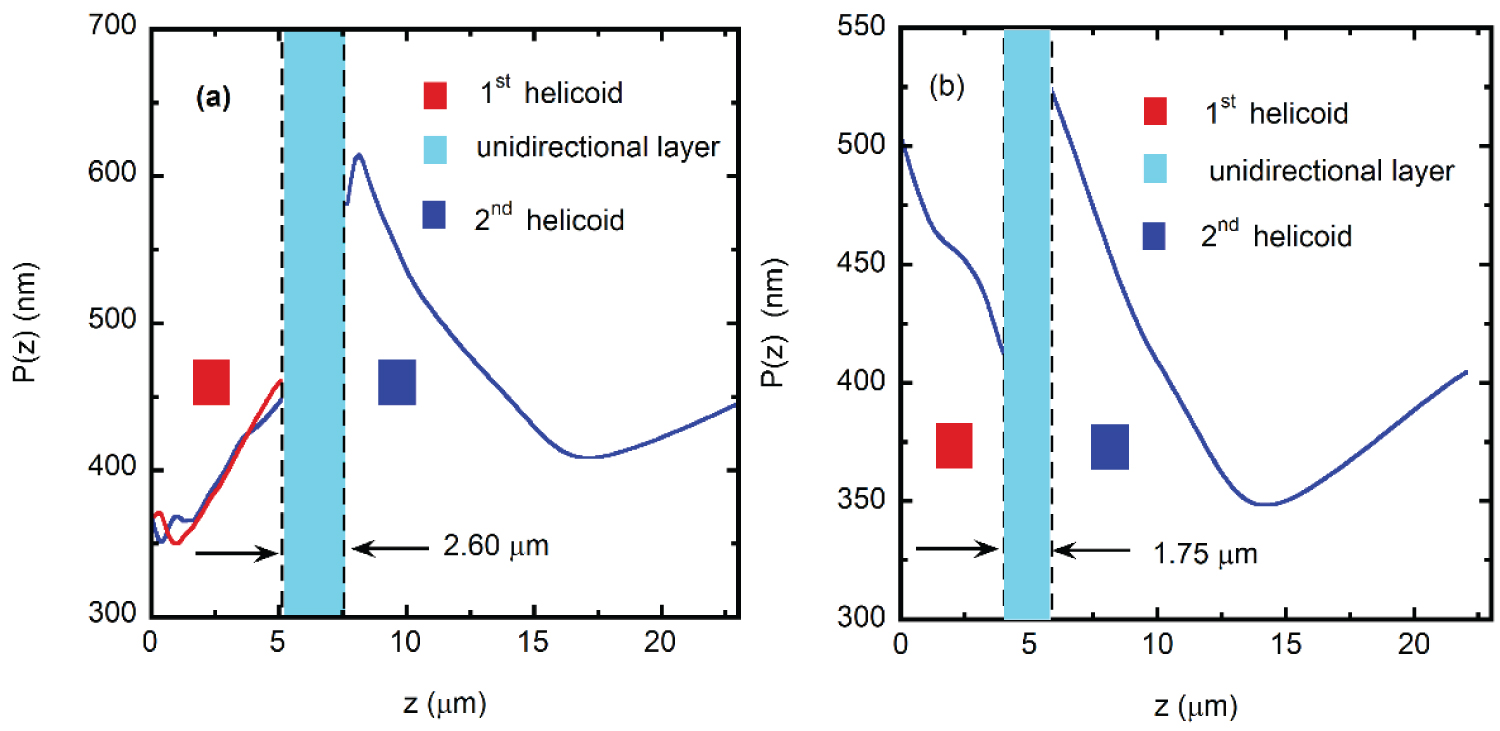
As mentioned before, Caveney's analysis based on electron microscopy reveals the presence of the epicuticle, a waxy coating layer of thickness e, a helicoidal structure 5.1 μm thick with left chirality followed by a 1.8 μm thick unidirectional layer, and a second thicker left-handed twisted structure with 16.5 μm in thickness [20]. Following Caveney's notation, we denote these thicknesses as h₁, u, and h₂, respectively. From more recent analysis, e = 0.60 µm, h₁ = 4.4 µm, u =1.6 µm, and h₂ = 15.0 µm [25]. Our own estimations are e = 0.60 µm, h₁ = 5.1 µm, u = 2.6 µm, and h₂ = 15.4 µm. Similar ratios h₁/u and h₂/u are found for the two previously reported cases with values close to h₁/u = 2.8 and h₂/u = 9.3. From our analysis h₁/u = 2.0 and h₂/u = 6.0. We obtained these values from the SEM image shown in Figure 7. The flat epicuticle is shown at the top of the figure, which is followed by a chiral structure which consists of a sequence of lamellae formed by oriented fibrils of the chitin biopolymer [42]. Then, a unidirectional layer is displayed followed by a second helicoidal structure. The chitin fibrils gradually change their orientations in π radians every two successive green lines which corresponds to a lamella. In this way, and using the scale shown at the bottom right side of the image, we obtain the dependence on depth z of the azimuth angle specifying the orientation of the chitin fibrils, i.e, φ = φ(z). This angle is crucial as it is the parameter that goes into radiative transfer calculations. The uncertainty in z gives P(z)-values with uncertainties close to 5 nm. For the first helicoidal structure, z is measure from the bottom of the epicuticle, it is measured from the bottom of the unidirectional layer for the second arrangement.

When considering assumed z-dependent effective pitches in the context of calculations based on Berreman's formalism or on finite element methods, the azimuth angle is obtained from the effective pitch or spatial period: φ(z) = 2πz/P(z) [43,44]. But, when the available information, obtained from electron microscopy images, is the z-dependence of the azimuth angle, the effective pitch is obtained from P(z) = 2πz/φ(z). In this way, the effective or average pitch is equal to the inverse of the average density of turns up to depth z, namely P(z) = 1/[n/z] with n being the number of turns of the helical structure up to depth z. This effective pitch will be referred as the pitch through what follows. Another approach obtains the structural pitch from the inverse of the local density of turns, namely, Ps (z) = 1/[dn/dz] [45]. When φ(z) is obtained from φ(z) = 2πz/P_s(z) to be used in the radiative transfer model, leads to calculated reflectance spectra more spectrally structured than those measured (see Figure 4 in [31] and Figure 3a in [25] for comparison purposes when considering reflectance spectra of C. resplendens' cuticle, with emphasis on the RHCP component linked with the spatial variation of the pitch through the second helicoidal structure). Within Berreman's formalism, the pitch to be used is the effective one, P(z), as shown in next Section. The method described to obtain P(z) from SEM or TEM images can also be applied after extracting data from graphs of the lamellar pitch profile versus the number of half turns made by the helical structure (see for example Figure 3 in [20], Figure 7.5 in [22], and Figure 2 in [25]).

Significant differences in the pitch profile of C. resplendens are reported in the literature, particularly for the first helicoidal structure: Caveney reported an increase of the lamellar pitch with the number of half turns carried out by the first twisted structure [20], while McDonald and Finlayson data show a decrease [22,25]. Our own analysis is closer to Caveney's results who had at his disposal museum specimens for the analysis. At this point it becomes essential to have a taxonomic identification of the specimens being analyzed. Figure 8a displays the effective pitch depth dependence obtained from the analysis of Figure 7, and that obtained by averaging the data extracted from Figure 7.5 of [22] is shown in Figure 8b. Our P(z)-data shows variations in both the first and second helicoidal arrangements, as shown by the blue and red lines in Figure 8a, particularly through the first 1.8 μm in depth. For the two pitch variations displayed for the first helicoid, the average pitch is P_avg,1 = 395 nm. For the second helicoid, the pitch average value is P_avg,2 = 464 nm. The cuticle's morphology basically differs in the z-dependence of the pitch through the first helicoidal section, in the position of the unidirectional layer, and in its thickness. Differences in the second helicoid are mainly shown right after the unidirectional layer. Beyond, similar z-dependences of the pitches are displayed for both specimens, with a minimum value at a depth close to 15 μm. The average pitch of the specimen captured near Tenorio volcano shows values between about 350 and 612 nm. For the specimen considered in [22], the average pitch is between 350 and 520 nm. As mentioned above, the unidirectional layer, which is analogous to a nematic liquid crystal phase, behaves like an HWP, particularly for that wavelength λ_HWP satisfying the relation Γ = (2πu/λ_HWP)Δn = π, with Γ as the retarded phase [46], and Δn = n_e-n_o as the effective birefringence, n_e and n_o being the extraordinary and ordinary refractive indices of the anisotropic uniaxial medium [47]. From the average birefringence in the unidirectional layer reported for the Caveney specimen, Δn = 0.166, and the thickness of the unidirectional layer, u = 1.8 μm [20], the optimal wavelength of the HWP retarder is λ_HWP = 598 nm. From his data in Figure 5b, one also can calculate γ = R_LHCP/R_RHCP = 0.68 at 598 nm with R_RHCP = 0.35, and γ = 1 at 569 nm with R_LHCP = R_RHCP = 0.32 [20].

The optical properties of the cuticle depend on the morphological arrangements through the z-dependence of the pitches, as well as the refractive indices of chitin and uric acid [48,49]. Birefringence of these materials also plays a fundamental role. The spectral variation of the chitin's birefringence Δn_c has been reported in the literature [50], with an average value equal to 0.0026 through the visible and near infrared wavelength ranges. The average birefringence of uric acid for visible wavelengths has been reported to be 0.31 [51]. Within a modeling approach of the optical constants of C. resplendens' cuticle, Mendoza-Galván, et al. have obtained, from an ellipsometry analysis, the spectral variation of the retarded phase Γ due to the unidirectional layer [31]. From modeling the effective birefringence by Δn=ua>Δn_ua+(1-ua>)Δn_c (with ua> as the average volume fraction of uric acid), using the average volume fraction of uric acid as fitting parameter whose value is adjusted to obtain a spectral average value of 0.31 for the uric acid's birefringence for visible wavelengths, we have obtained ua> = 0.41, with u = 1.75 µm as thickness of the retarder layer reported in [31]. Caveney's reports of the whole average uric acid volume fraction and thickness of the unidirectional layer are =0.70 and u=1.8 mm [20], respectively. Spatial dispersion in the average concentration of uric acid and thickness of the retarder layer can be contributing to the variability in the measured reflectance spectra.

Relation between Effective and Structural Pitches

As explained in the previous Section, we obtain from SEM images the variation of the azimuth angle with depth, φ = φ (z), at those depths where half turns are completed. In the radiative transfer calculations based on Berreman's formalism [52] or in finite element methods [44], the azimuth angle φ(z) enters in the expressions of the dielectric function tensor components characterizing the optically anisotropic material (see Equation 61 in [52]). The use of the expression φ(z)=2πz/P(z) allows us to calculate an effective or average pitch P(z) from the previously obtained z-dependence of φ. Morphological comparisons can be made through the z-dependence of the pitches. We use interpolated values of P(z) to obtain corresponding values of φ(z). The z-dependence of the effective pitch is a key aspect to carry out the photonic crystal characterization according to the method devised by us. Another approach consists of obtaining the morphological or structural pitch P_s(z) from electron microscopy images, at those depths where each lamellar turn is completed. Interpolated values can be evaluated and then, the azimuth angle can be obtained from integration of dφ =2πdz/P_s (z) from 0 to z. Namely,

$$\varphi (z)-\varphi (z=0)={\displaystyle \underset{0}{\overset{z}{\int }}\frac{2\pi }{P_s(z)}dz}\text{ (1)}$$

Without loss of generality, with f(z=0)=0, a relation between the effective pitch and the structural one is obtained by:

$$\frac{2\pi z}{P(z)}={\displaystyle \underset{0}{\overset{z}{\int }}\frac{2\pi }{P_s(z)}dz}\text{ (2)}$$

Therefore $1/P(z)=〈1/P_s(z)〉$ and

$$\frac{1}{P_s(z)}=\frac{d}{dz}\left[\frac{z}{P(z)}\right]\text{ (3)}$$

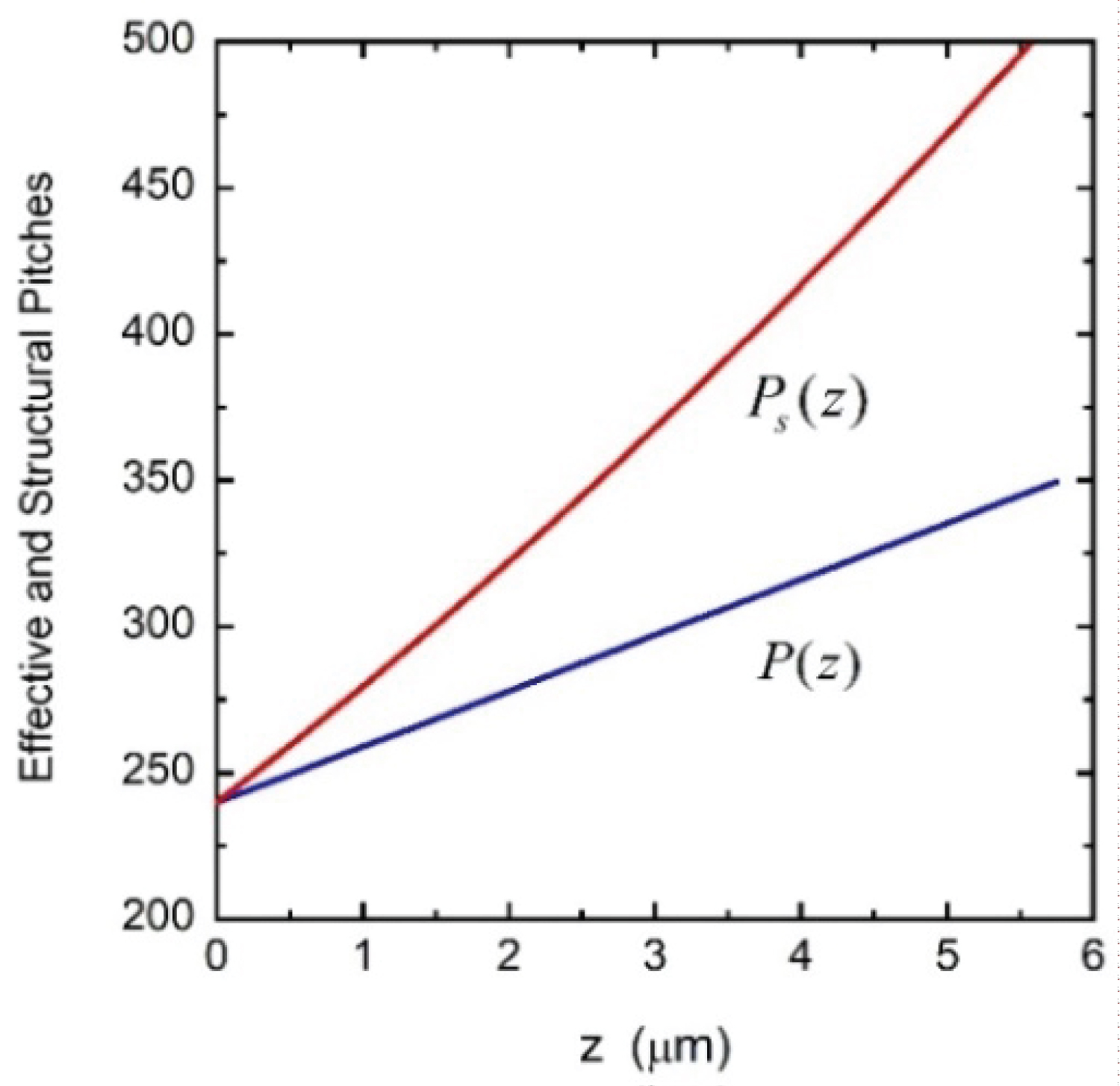
The pitch that could be directly involved in obtaining interpolated values of φ(z) is the effective pitch, not the structural one. This latter would be involved through the average value of its inverse which in fact gives the inverse of the effective pitch. This issue was not recognized or clearly established by many authors whose research works have served as valuable references in this field of physical optics [43,44,52]. As Berreman stated, they used the word pitch with no distinction between effective or structural when using the equation φ(z)=2πz/P(z) to evaluate the components of the dielectric function tensor to be used in radiative transfer calculations, or in finite element methods. Through all our previous publications where we used Berreman's formalism to evaluate reflectance spectra of twisted structures, the pitch we used is the effective one [53-56]. For example, in the context of the calculations carried out by Hong, et al. using finite element methods [44], the pitch assumed for one of their examples is P(z) = P_o(1+ az/H) with a = 0.458, P_o = 240 nm, and H = 24Po. With this P(z) they obtain φ(z)=2πz/P(z) to calculate the corresponding reflectance spectrum (see Figure 6 in their publication). The pitch used by them must be understood as an effective or average pitch. We have reproduced from Berreman's formalism the same results by calculating the azimuth angle in the same way (see Figure 7 in [56]). The corresponding structural or morphological pitch is P_s(z)=P_o(1+az/H)², according to Equation (3). Figure 9 displayed both pitches: the effective or average pitch P(z) and the structural or morphological one P_s(z).

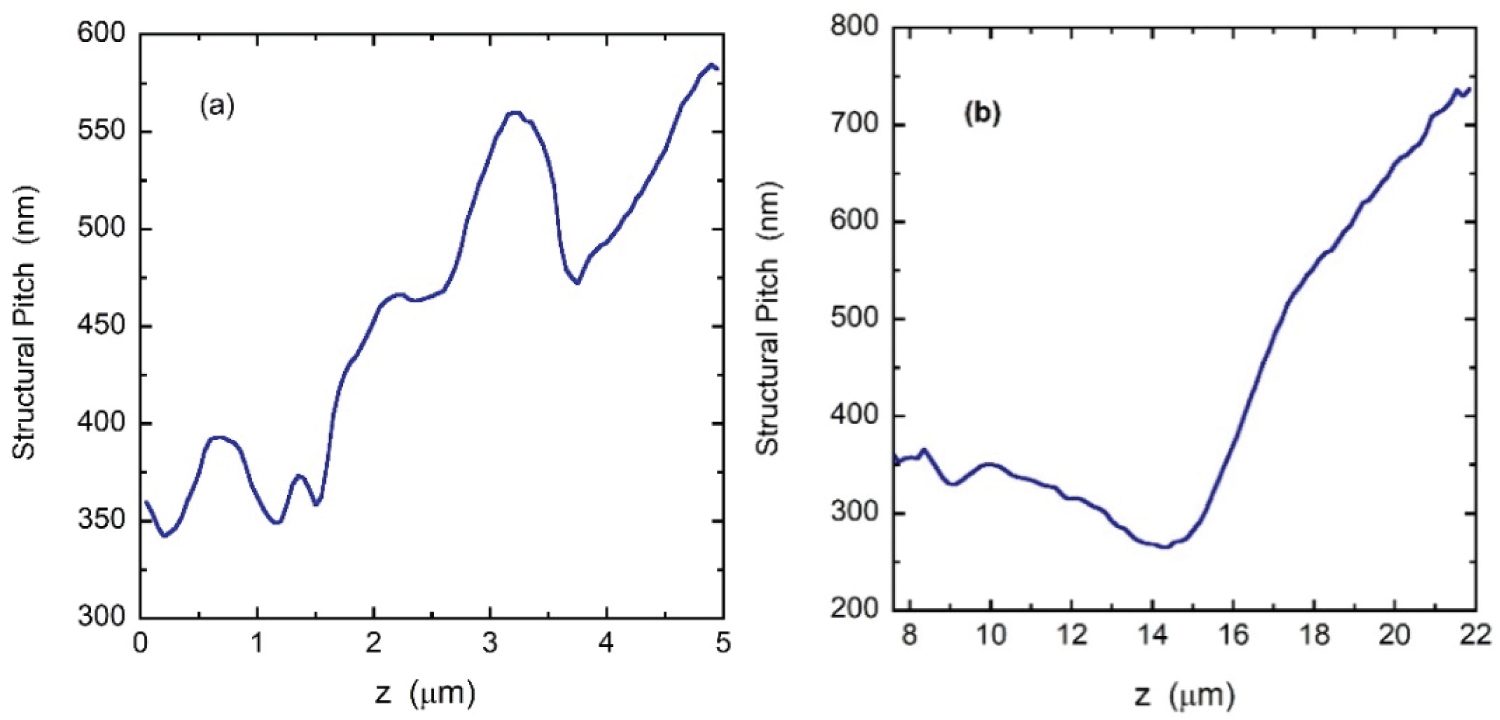
The Equation (3) is very appropriate to obtain the structural pitch once evaluated the effective one from φ(z). We applied this method to obtain the two structural pitches characterizing the chiral structures of the C. resplendens. The derivatives involved have been numerically evaluated from the data used to display Figure 8a. Figure 10a shows the results for the first helicoidal arrangement. This structural pitch approaches that reported by Caveney [20], but it differs substantially from that reported by McDonald [21], Finlayson, et al. [25] and Mendoza-Galván, et al. [30] which predominantly decreases with depth through the first twisted structure. The structural pitch of the second helicoid is displayed in Figure 10b. Under normal illumination, the spectral position of the PBG is given by λ_o= nav(λ_o) P_o for a twisted structure with a single pitch value P_o. For a graded twisted arrangement of structural pitch P_s(z), the spectral position of the PBG can be obtained from λ_o(z) = n_av(λ_o,z)P_s(z), with nav(λ_o,z) as the average refractive index at those wavelengths of the photonic band gap and at each dept z.

Summary and Conclusions

The optical properties of cuticles of C. resplendens scarab beetles have been qualitatively considered from its connection with the structural internal morphology of the elytra. Spectral measurements of total reflectance, as well as left- and right-handed circularly polarized light reflected by these cuticles of C. resplendens scarabs show significant variability depending on the position of the illuminated site on the elytron, the specific specimen considered, and the magnitude of the illuminated area. These facts suggest an intrinsic variability of the volume concentration of uric acid through the whole twisted structure which consists of a first helicoidal arrangement followed by a unidirectional retarder layer and a second thicker helicoidal section. Other characteristics that could be contributing to the variability in the optical measurements are the thickness of the unidirectional layer and the dependence with depth of the pitches of both twisted structures. In a second paper, the optical measurements and the pitch characterizations will be the starting points to model the reflectance spectra by Berreman's formalism incorporating, as much as possible, the inferred variability through the z-dependence of the pitches and the uric acid volume fraction, as well as variability in the thickness of the unidirectional layer. The analysis will be completed with the photonic crystal characterization of both chiral structures in the cuticle of C. resplendens beetles. The variability of the measured reflectance spectra documented in this work, as well as the explicit establishment of the correct relationship between effective and structural pitches, would be valuable information when considering the task of modelling and developing functional materials capable of reflecting both components of circular polarization, these components being tuned according to requirements of the specific applications in mind. The use of optically isotropic synthetic materials polyester and polyamide, for example, to design and to manufacture laminated fibers has successfully reached the laboratory stage [57]. The next level is scaling it. The reflectance spectra of these materials can be modelled within the context of radiative transfer through multilayers. The color of the layered structure can be a priori tuned by choosing adequately the thickness of the layers and the refractive indices of the materials involved. The use of optically anisotropic synthetic materials cholesteric liquid crystals and cellulose nanocrystals, for example, is in the laboratory stage [9,58]. The systematic tuning of the LHCP- and RHCP-reflectance spectra will be based on radiative transfer formalisms which incorporate the depth dependence of the effective pitch as well as its spatial variability or degree of disorder.

Acknowledgements

The authors thank the support given by the University of Costa Rica to carry out this research work. The authors also thank to Ewan D. Finlayson, at the University of Exeter in the United Kingdom, for kindly sharing the original data used to display the Figure 5c of this article [25].

References

1. Monzón-Sierra J, García-Morales LJ (2011) Two new species of Chrysina Kirby coleoptera: Scarabaeidae: Rutelinae from mexico. Insecta Mundi 0195: 1-8.
2. Monzón-Sierra J (2017) Four new species of Chrysina Kirby Coleoptera: Scarabaeidae: Rutelinae from Guatemala and Honduras. Insecta Mundi 0543: 1-12.
3. Hawks DC (2017) Five new species of Chrisyna Kirby Coleoptera: Scarabaeidae: Rutelinae. Insecta Mundi 0544: 1-9.
4. Mora-Aguilar EF, Curoe D, Delgado L, et al. (2018) A new Mexican species of Chrysina Kirby Coleoptera: Scarabaeidae: Rutelinae, with nomenclatural changes, new records, and a key to C quiche species group. Zootaxa 4461: 196-204.
5. Arwin H, Fernández del Río L, Åkerlind C, et al. (2017) On the polarization of light reflected from beetle cuticle. Materials Today: Proceedings 4: 4933-4941.
6. McDonald LT, Finlayson ED, Wilts BD, et al. (2017) Circularly polarized reflection from the scarab beetle chalcothea smaragdina: Light scattering by a dual photonic structure. Interface Focus 7: 20160129.
7. Cook CQ, Ami A (2016) Theory of chirped photonic crystals in biological broadband reflectors. Optica 3: 1436-1439.
8. Song MH, Park B, Shin KC, et al. (2004) Effect of phase retardation on defect-mode lasing in polymeric cholesteric liquid crystals. Adv Mat 16: 779-783.
9. Matranga A, Baig S, Boland J, et al. (2013) Biomimetic reflectors fabricated using self-organizing self-aligning liquid crystal polymers. Adv Mat 25: 520-523.
10. Jullien A, Neradovskiy M, Scarangella A, et al. (2020) Biomimicry of iridescent, patterned insect cuticles: comparison of biological and synthetic, cholesteric microcells using hyperspectral imaging. J R Soc Interface 17: 20200239.
11. Wang L, Urbas AM, Li Q, et al. (2018) Nature-inspired emerging chiral liquid crystal nanostructures: From molecular self-assembly to DNA mesophase and nanocolloids. Adv Mat 32: 1801335.
12. Rofouie P, Alizadehgiashi M, Mundoor H, (2018) Self-assembly of cellulose nanocrystal into semi-spherical photonic cholesteric films. Adv Funct Mat 28: 1893852.
13. Chan CLC, Bay MM, Jacucci G, et al. (2019) Visual appearance of chiral nematic cellulose-based photonic films: Angular and polarization independent color response with a twist. Adv. Mat 31: 1905151.
14. Scarangella A, Soldan V, Mitov M (2020) Biomimetic design of iridescent insect cuticles with tailored, self-organized cholesteric patterns. Nat Commun 11: 4108.
15. Wood SM, Fells JAJ, Elston SJ, et al. (2016) Wavelength tuning of the photonic band gap of an achiral nematic liquid crystal filled into a chiral polymer scaffold. Macromolecules 49: 8643-8652.
16. Pye JD (2010) The distribution of circularly polarized light reflection in the Scarabaeoidea Coleoptera. Biological Journal of the Linnean Society 100: 585-596.
17. Boucard A (1875) Monographic list of the Coleoptera of the genus Plusiotis of America, North of Panama, with descriptions of several new species. Proc Zool Soc Lond XXIII: 117-125.
18. Michelson AA (1911) On metallic colouring in birds and insects. The London, Edinburgh, and Dubling Philosophical Magazine and Journal of Science 21: 554-567.
19. Frederick R (2017) An unusual shimmer. American Scientist 105: 268-269.
20. Caveney S (1971) Cuticle reflectivity and optical activity in scarab beetles: The role of uric acid. Proc Ro Soc Lond B 178: 205-225.
21. Kinoshita S (2008) Structural Colors in the Realm of Nature. World Scientific, London.
22. McDonald LT (2016) Circularly polarized optics in Scarabaeidae. Doctoral Thesis, University of Exeter, United Kingdom.
23. Goldstein DH (2006) Polarization properties of Scarabaeidae. Appl Opt 45: 7944-7950.
24. McDonald LT, Starkey TA, Vukusic P, et al. (2014) Photonic architectures in beetles: Twists and iridescence. Int J Design & Nature Ecodynamics 9: 266-275.
25. Finlayson ED, McDonald LT, Vukusic P, et al. (2017) Optically ambidextrous circularly polarized reflection from the chiral cuticle of the scarab beetle Chrysina resplendens. J R Soc Interface 14: 20170129.
26. Bagge LE, Kenton AC, Lyons BA, et al. (2020) Mueller matrix characterizations of circularly polarized reflections from golden scarab beetles. Appl Opt 59: F85-F93.
27. Carter IE (2017) An experimental study in the variation of the near-circular polarization properties in Scarabaeoidae beetles. Doctoral Thesis, Imperial College, London, United Kingdom.
28. Hodgkinson I, Lowrey S, Bourke L, et al. (2010) Mueller-matrix characterization of beetle cuticle: Polarized and unpolarized reflections from representative architectures. Appl Opt 49: 4558-4567.
29. Hegedüs R, Szél G, Horváth G, et al. (2006) Imaging polarimetry of the circularly polarizing cuticle of scarab beetles Coleoptera: Rutelidae, Cenoniidae. Vision Research 46: 2786-2797.
30. Fernández del Río L, Arwin H, Järrendahl K, et al. (2016) Polarizing properties and structure of the cuticle of scarab beetles from the Chrysina genus. Phys Rev E 94: 012409.
31. Mendoza-Galván A, Järrendahl K, Arwin H, et al. (2019) Mueller-matrix modeling of the architecture in the cuticle of the beetle Chrysina resplendens. J Vac Sci Technol. B 37: 062904.
32. Berthier S (2007) Iridescences: The Physical Colors of Insects. Springer, New York, Chapter 4.
33. Richards AG (1951) The Integument of Arthropods. University of Minnesota Press, Minneapolis, Chapter 16.
34. Pace A (1972) Cholesteric liquid crystal-like structure of the cuticle of Plusiotis gloriosa. Science 176: 678-680.
35. Jullien A, Neradovskiy M, Mitov M, et al. (2020) Hyperspectral topography of the twisted, cholesteric patterns of an insect cuticle under various conditions of helix obliquity. APL Photon 5: 096102.
36. Agez G, Bitar R, Mitov M, et al. (2011) Color selectivity lent to a cholesteric liquid crystal by monitoring interface-induced deformations. Soft Matter 7: 2841-2847.
37. Hooper IR, Vukusic P, Wootton RJ, et al. (2006) Detailed optical study of the transparent wing membranes of the dragongly Aeshna cyanea. Opt Express 14: 4891-4897.
38. Mendoza-Galván A, Fernández del Río L, Järrendahl K, et al. (2018) Graded pitch profile for the helicoidal broadband reflector and left-handed circularly polarizing cuticle of the scarab beetle Chrysina chrysargyrea. Sci Rep 8: 6456.
39. Campos-Fernández C, Azofeifa DE, Hernández-Jiménez M, et al. (2011) Visible light reflection spectra from cuticle layered materials. Opt Mat Express 1: 85-100.
40. Bouligand Y (2008) Liquid crystals and biological morphogenesis: Ancient and new questions. C. R. Chimie 11: 281-296.
41. Hernández-Jiménez M, Azofeifa DE, Libby E, et al. (2014) Qualitative correlation between structural chirality through the cuticle of Chrysina aurigans scarabs and left-handed circular polarization of the reflected light. Opt Mat Express 4: 2632-2645.
42. Barzic AI, R, Albu M, et al. (2020) Optical properties and biointerface interactions of chitin. Polymer Bulletin.
43. Lu Z, Li L, Vithana H, et al. (1997) Optical properties of single layer non-absorptive broad band CLC polarizers. Mol Cryst Liq Cryst. 301: 237-248.
44. Hong Q, Wu TX, Wu ST, et al. (2003) Optical wave propagation in a cholesteric liquid crystal using the finite element method. Liquid Crystals 30: 367-375.
45. Mendoza-Galván A, Järrendahl K, Arwin H, et al. (2019) Graded circular Bragg reflectors: A semi-analytical retrieval of approximate pitch profiles from Mueller-matrix data. J Opt 21: 125401.
46. Yeh P (2005) Optical Waves in Layered Media. Wiley Interscience, New Jersey.
47. Hecht E (2017) Optics. Pearson Education, England.
48. Azofeifa DE, Arguedas HJ, Vargas WE, et al. (2012) Optical properties of chitin and chitosan biopolymers with application to structural color analysis. Opt Mat 35: 175-183.
49. Vargas WE, Azofeifa DE, Arguedas HJ, et al. (2013) Refractive índices of chitin, chitosan, and uric acid with application to structural color analysis. Óptica Pura & Aplicada 46: 55-72.
50. Mendoza-Galván A, Muñoz-Pineda E, Järrendahl K, et al. (2016) Birefringence of nanocrystalline chitin films studied by Mueller-matrix spectroscopy ellipsometry. Opt Mat Express 6: 671-681.
51. Ringertz H (1965) Optical and crystallographic data of uric acid and its dihydrate. Acta Cryst 19: 286-287.
52. Berreman DW (1972) Optics in stratified and anisotropic media: 4 × 4-matrix formulation. J Opt Soc Am 62: 502-510.
53. Libby E, Azofeifa DE, Hernández-Jiménez M, et al. (2014) Light reflection by the cuticle of C. aurigans scarabs: A biological broadband reflector of left-handed circularly polarized light. J Opt 16: 082001.
54. Vargas WE, Hernández-Jiménez M, Libby E, et al. (2015) Broadening of effective photonic band gaps in biological chiral structures: From intrinsic narrow band gaps to broad band reflection spectra. European Physics Letters 111: 64001.
55. Vargas WE, Hernández-Jiménez M, Libby E, et al. (2016) Light reflection by cuticles of Chrysina jewel scarabs: optical measurements, morphology characterization, and theoretical modeling 9. Optics & Photonics Journal 6: 146-163.
56. Vargas WE, Avendano E, Hernández-Jiménez M, et al. (2018) Photonic crystal characterization of the cuticles of Chrysina chrysargyrea and Chrysina optima jewel scarab beetles. Biomimetics 3: 3040030.
57. Kinoshita S, Yoshioka S (2005) Structural Colors in Biological Systems. Osaka University Press Japan.
58. Frka-Petesic B, Radavidson H, Jean B, et al. (2017) Dynamically controlled iridescence of cholesteric cellulose nanocrystal suspensions using electric fields. Adv Mater 29: 1606208.