Performance of Differential Carrier Phase Recovery for QPSK Modulation Format
Abstract
Differential carrier phase recovery for QPSK modulation format is implemented in a field-programmable gated array (FPGA) to compensate for laser phase noise. Real-time digital signal processing implemented in the FPGA demonstrates that combined linewidth symbol duration product of 10-3 can be tolerated with a sensitivity penalty of 3 dB at a BER of 10-3. The impact of the number of bits processed by the coordinate rotational digital computer (CORDIC) algorithm for the differential carrier phase recovery is also investigated. Finally, the performance of the proposed algorithm in the presence of frequency offset is presented through simulation.
Keywords
Carrier phase recovery, QPSK modulation format, Field-programmable gated array (FPGA)
Introduction
Advanced modulation formats in combination with digital coherent receivers are currently receiving significant attention for the next-generation of optical communication systems [1]. In particular, the QPSK modulation format has attracted a lot of research interest to increase data capacity for long-haul communication systems due to its robustness to linear impairments and optical signal-to-noise ratio requirements [2,3]. With coherent detection, it becomes possible to compensate for various impairments in the digital domain including phase noise contributions from the transmitter laser and the local oscillator (LO). Laser phase noise is known to have a limiting effect on the performance of optical coherent systems. There-fore, digital carrier phase estimation is indispensable for QPSK coherent receivers with a free-running LO without an optical phase locked loop [4].
Several carrier phase estimation algorithms have been proposed in the literature [5-10] for the QPSK modulation format with the Viterbi and Viterbi phase estimation (VVPE) being the most commonly employed technique which raises the received symbols to the power of four to wipe off the data modulation. The modulation-free signals are then summed over a block of data to reduce the impact of amplified spontaneous emission (ASE) noise on the phase estimation followed by phase unwrapping to track the trajectory of the physical phase.
The differential carrier phase recovery algorithm was demonstrated in [11] using full-precision arithmetic. The simulated performance of the differential algorithm was compared to the VVPE using the measured phase noise for an integrated tunable laser. In this paper, the real-time performance of the differential carrier phase recovery algorithm is investigated in a field-programmable gated array (FPGA) for the QPSK modulation format. An arbitrary waveform generator (AWG) is used to emulate the QPSK signals with different values of combined line width symbol duration product, Δν.Ts, and signal-to-noise ratio (SNR). It is shown that direct differential decoding can successfully compensate for Δν.Ts of 10-3 with a sensitivity penalty of 3 dB at a BER of 10-3. The impact of different data widths on the performance of the coordinate rotational digital computer (CORDIC) algorithm is also investigated. Finally, the performance of the differential carrier phase recovery is simulated in the presence of frequency offset between the transmitter laser and the LO.
Optical Coherent Systems and Carrier Phase Recovery
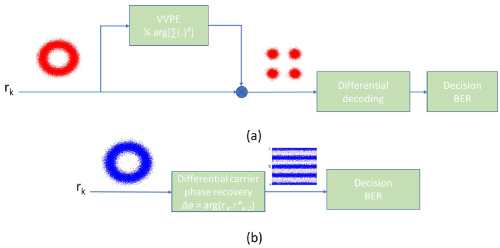
The block diagram of an optical coherent system is shown in Figure 1. A bit pattern generator is used to drive an optical IQ modulator to generate the optical signal for transmission over the optical fibre. On the receiver side, an optical 90° hybrid is used with a local oscillator (LO) to extract the in-phase and quadrature components of the received signal. The data captured by the real-time oscilloscope is compensated for various transmission impairments using digital signal processing (DSP) algorithms. In this paper, the compensation of phase noise for the QPSK modulation format is discussed using direct differential de-coding on the optical field measured by a coherent receiver as opposed to the VVPE followed by differential decoding. The VVPE is a widely adopted scheme for the QPSK modulation format in digital coherent receivers for carrier phase recovery. The estimated phase, Φ, using the VVPE can be obtained using [9].
where Nb is the averaging block size. The VVPE is followed by differential de-coding to solve the four-fold phase ambiguity and also to avoid cycle slips. The VVPE algorithm is compared to the differential carrier phase recovery algorithm in Figure 2.
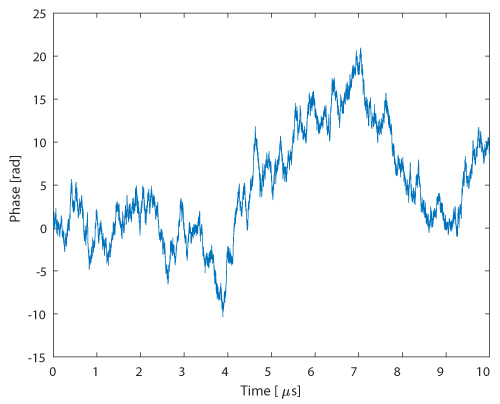
As can be seen in Figure 2b, the power of four operations is not needed when using the differential carrier phase recovery algorithm. The phase noise in a 10 Gbaud optical coherent system is shown in Figure 3 for a combined linewidth of 10 MHz for the transmitter laser and the LO at the coherent receiver. This corresponds to combined linewidth symbol duration product, Δν.Ts, of 10-3. In this paper, the real-time implementation of the differential carrier phase recovery algorithm is investigated in a field-programmable gated array (FPGA) for different combined linewidth symbol duration product. The impact of the number of bits used for the differential carrier phase recovery is also investigated when using the CORDIC algorithm on the FPGA.
Real-Time Differential Carrier Phase Recovery
Following the compensation of various impairments in a typical QPSK coherent system and the frequency offset between the transmitter laser and the LO, the phase noise associated with the received signals, rk, can be mitigated using.
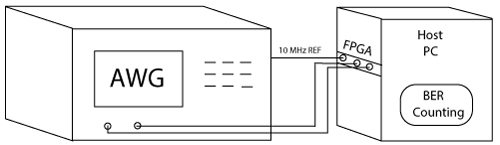
which is a direct differential decoding on the optical field measured by a coherent receiver. As can be seen in Figure 1, the transmitter laser and the LO contribute to the phase noise in the transmission system. In contrast to the VVPE, the algorithm (2) does not require the power of four operation to remove the data modulation, averaging or phase unwrapping for carrier phase recovery. The performance of the differential carrier phase recovery algorithm (2) was investigated using the experimental setup shown in Figure 4.
An arbitrary waveform generator (AWG) was used to emulate the QPSK signals with different values of Δν.Ts and signal-to-noise ratio (SNR). The phase noise from the transmitter laser and the LO was modeled as the Wiener process [8].
where νi's are independent and identically distributed (i.i.d) random Gaussian variables with zero mean and variance,
and Δν is the combined linewidth of the transmitter laser and the LO. The two data streams, corresponding to the I- and Q-channels, were differentially encoded as shown in Table 1 and transmitted using the AWG.
Two analog-to-digital converter (ADCs) with 12 bits resolution integrated on a FPGA evaluation board were used to capture the I- and Q-data streams from the AWG at 1.6 GSamples/s (2 samples/symbol). The received samples were fed to a Virtex 6 FPGA to implement the differential carrier phase recovery algorithm (2). The samples were represented in signed two's complement format and were first corrected for gain and offset error to compensate for imperfections in the ADCs. Eight samples synchronized to a 200 MHz clock (sampling frequency/8) were available for parallel signal processing. The clock signal was generated on the FPGA evaluation board using a 10 MHz reference signal from the AWG. Therefore, no clock recovery was required in this work.
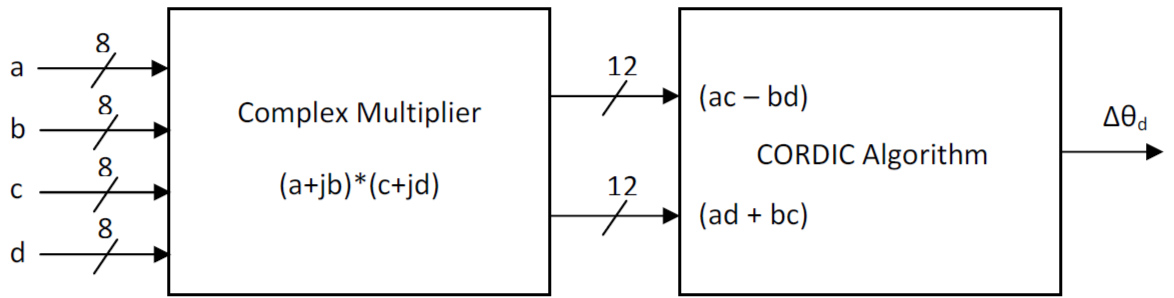
The block diagram of the FPGA implementation is shown in Figure 5. Only the 8 most significant bits (MSBs) of the ADC samples for the I- and Q-channels were processed by the complex multiplier corresponding to the minimum data widths required at the input ports. The arg(.) operation in (2) was achieved using the CORDIC algorithm. The output widths of the complex multiplier were truncated from the 17-bits output full-precision product to 12 MSBs to compute Δθd in (2) as a compromise amongst performance, logic resources, and meeting constraints. The data streams at the output of the CORDIC block were then transferred to a host computer for BER counting using PCI Express interfaced with 8 Multi-Gigabit transceivers.
Results and Discussion
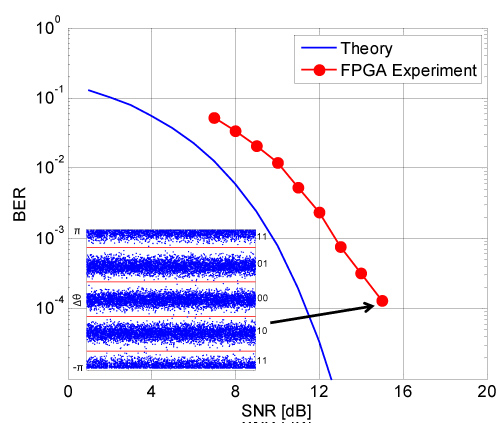
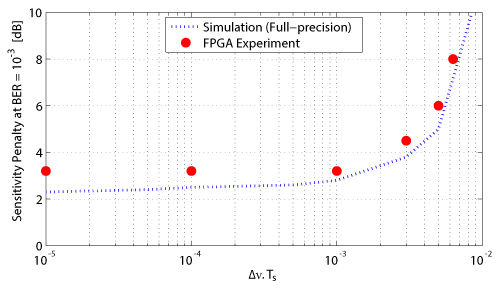
The real-time performance of the differential carrier phase recovery algorithm (2) is shown in Figure 6 for Δν.Ts = 10-3 with the data processed in the FPGA. The theoretical BER curve is also shown for comparison. The penalty at a BER of 10-3 was found to be 3 dB. No BER floor was observed close to the BER of 10-3 with Δν.Ts = 10-3. The inset in Figure 6 shows the samples from the output of the CORDIC block transferred to the host computer along with the decision boundaries to decode the transmitted bits. The sensitivity penalty at a BER of 10-3 for different Δν.Ts is shown in Figure 7 when using algorithm (2) for carrier phase recovery and the AWG as discussed above. The simulated performance is also shown for comparison. As can be seen in Figure 7, the additional implementation penalty in hardware is only 0.4 dB for Δν.Ts = 10-3 compared to full-precision arithmetic in the simulation.
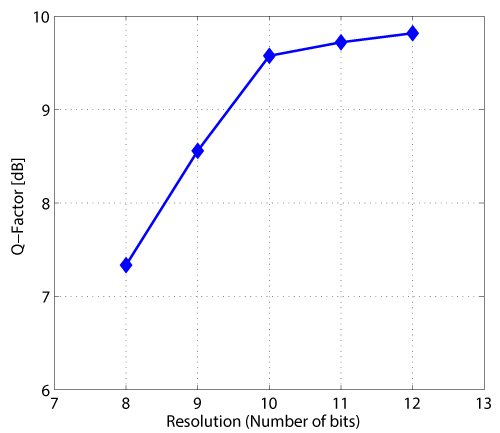
Next, the performance of the CORDIC algorithm in the FPGA was investigated for different input data widths. The MSBs from the complex multiplier were truncated from 12 to 8 bits to compute the arg(.) operation in (2). The performance of the algorithm is shown in Figure 8 and the penalty was found to be > 1 dB in the Q-Factor for data widths lower than 10 bits resolution.
Finally, the performance of the differential carrier phase recovery algorithm was simulated in the presence of frequency offset, ΔF, between the transmitter laser and the LO. The frequency offset was estimated using [12].
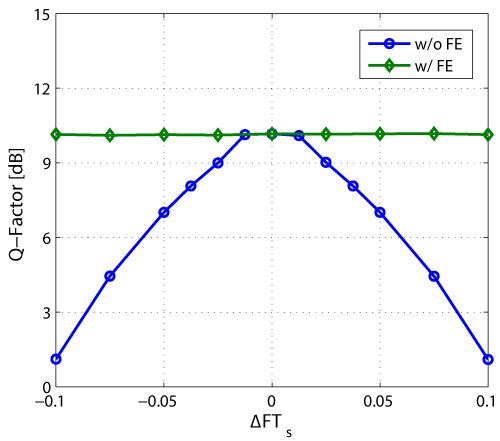
where N is the block size. Figure 9 shows the degradation in the Q-factor with and without frequency estimation with Δν.Ts = 10-3 and SNR of 13 dB. The value of N was set to 128 in the simulation. The transmitted symbols were successfully recovered when using (5) with the differential carrier phase recovery algorithm shown in Figure 2b. The BER performance for the QPSK modulation format was found to degrade significantly for ΔF.Ts > 0.02 without frequency estimation.
It is noted that the direct differential decoding on the optical field avoids the four-fold phase ambiguity associated with the VVPE, cycle slips and catastrophic failure for the QPSK modulation format. The differential carrier recovery can also be adapted for high-speed data processing as it does not contain any feedback loop.
Conclusions
The real-time performance of the differential carrier phase recovery algorithm has been investigated in a field-programmable gated array (FPGA) for the QPSK modulation format with the laser phase noise fluctuations emulated by an arbitrary waveform generator. It is shown that the direct differential decoding on the optical field measured by a coherent receiver can successfully compensate for combined linewidth symbol duration product of 10-3 with a sensitivity penalty of 3 dB at a BER of 10-3. Compared to the VVPE, the differential algorithm does not require the power of four operation to remove the data modulation, averaging or phase unwrapping for carrier phase recovery. The performance of the algorithm has also been investigated in the presence of frequency offset between the transmitter laser and the local oscillator. The impact of the number of bits used for the differential carrier phase recovery has also been demonstrated when using the CORDIC algorithm on the FPGA.
Acknowledgment
This work was supported by BEIS and the European Union's Horizon 2020 research and innovation programme under grant agreement 761579 (TERAPOD).
References
- Yang T, Shi C, Chen X, et al. (2018) Linewidth-tolerant and multi-format carrier phase estimation schemes for coherent optical m-QAM flexible transmission systems. Opt Express 26: 10599-10615.
- Fatadin I, Savory SJ (2010) Impact of phase to amplitude noise conversion in coherent optical systems with digital dispersion compensation. Opt Ex-press 18: 16273-16278.
- Chris RS Fludger, Duthel T, Van Den Borne D, et al. (2008) Coherent Equalization and POLMUX-RZ-DQPSK for Robust 100-GE Transmission. Journal of Lightwave Technology 26: 64-72.
- Kazovsky LG, Kalogerakis G, Shaw WT (2006) Homodyne phase-shift-keying systems: past challenges and future opportunities. Journal of Lightwave Technology 24: 4876-4884.
- Ip E, Kahn JM (2007) Feedforward carrier recovery for coherent optical communications. Journal of Lightwave Technology 25: 2675-2692.
- Ip E, Lau APT, Barros DJF, et al. (2008) Coherent detection in optical fiber systems. Optics Express 16: 753-791.
- Taylor MG (2009) Phase estimation methods for optical coherent detection using digital signal processing. Journal of Lightwave Technology 27: 901-914.
- Pfau T, Hoffmann S, Noe R (2009) Hardware-efficient coherent digital receiver concept with feed forward carrier recovery for M -QAM Constellations. J Lightw Technol 27: 989-999.
- Ly-Gagnon DS, Tsukamoto S, Katoh K, et al. (2006) Coherent detection of optical quadrature phase-shift keying signals with carrier phase estimation. Journal of Lightwave Technology 24: 12-21.
- Seimetz M (2008) Laser linewidth limitations for optical systems with high-order modulation employing feed forward digital carrier phase estimation. OFC/NFOEC.
- Fatadin I, Ives D, Savory SJ (2013) Differential carrier phase recovery for QPSK optical coherent systems with integrated tunable lasers. Optics Express 21: 10166-10171.
- Fatadin I, Savory SJ (2011) Compensation of frequency offset for 16-QAM optical coherent systems using QPSK partitioning. IEEE Photonics Technology Letters 23: 1246-1248.
Corresponding Author
Dr. Irshaad Fatadin, National Physical Laboratory, Teddington, Middx, TW11 0LW, UK.
Copyright
© 2020 Fatadin I. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.