Superluminal Speed of Photons in the Electromagnetic Near-Field
Abstract
The possible existence of superluminal particles, which are forbidden by well-known laws of physics, has been studied by many physicists. Some of them confirmed the superluminal speed by their experiments. By using Klein-Gordon wave equation for photons, the author shows that the photon travels at a superluminal speed in an electromagnetic near field of the source and they reduce to the speed of light as they propagate into the far field.
Keywords
Photon, Near-field, Superluminal speed, Electromagnetic radiation
Introduction
E. Recami claimed in his paper [1] that tunneling photons traveling in evanescent mode can move with superluminal group speed inside the barrier. Chu and S. Wong at AT&T Bell Labs measured superluminal velocities for light traveling through the absorbing material [2]. Furthermore, Steinberg, Kwait and Chiao devised an experiment measuring the tunneling time for visible light through an optical filter, consisting of a multilayer coating about m thick, and confirmed superluminal speed [3]. The results obtained by Steinberg and co-workers have shown that the photons seemed to have traveled at 1.7 times the speed of light. Recent optical experiments at Princeton NEC have verified that superluminal pulse propagation can occur in transparent media [4]. These results indicate that the process of tunneling in quantum physics is indeed superluminal, as claimed by E. Recami. Caligiuri and Musha also confirmed the existence of superluminal photons in brain microtubules theoretically [5].
The photon is a type of elementary particle, the quantum of the electromagnetic field including electromagnetic radiation such as light, and the force carrier for the electromagnetic force. The photon has zero rest mass and always moves at the speed of light in vacuum. The single photons travel through space at the group velocity of light. The group velocity of the light wave is thought of as the velocity at which energy or information is conveyed along a wave. The electromagnetic field by photons consists of the near-field and far field around an object, such as a transmitting antenna, or the result of radiation scattering off an object. Far-field strength decreases inversely with distance from the source, resulting in an inverse-square law for the radiated power intensity of electromagnetic radiation. By contrast, near-field E and B strength decrease more rapidly with distance: The one part decreases by the inverse-distance squared, the other part by an inverse cubed law, resulting in a diminished power in the parts of the electric field by an inverse fourth-power and sixth-power, respectively.
The author published a paper that claimed a tiny particle compared with electrons like neutrinos might be generated as a superluminal particle [6]. In this paper, by applying Klein-Gordon equation, it is shown that photons are generated as a superluminal particle and moves at a superluminal speed (i.e. superluminal group velocity of the light wave) in the electromagnetic near-field from the source.
Wave Equation for the Superluminal Photon
From the wave function mathematical description of a particle, taking account the special theory of relativity, the Klein-Gordon equation is considered:
Where H is a Hamiltonian given by ( p : Momentum of the particle, m : Effective mass) and is a wave function of a particle. The following equation can be obtained for the accelerating particle [7]
Where is the Plank constant divided by , c is the speed of light, and a is a proper acceleration given by .
From Eq. (2), we have the solution given by [7]
Where C is an arbitrary constant.
By introducing the particle linear momentum , and the energy , we have
Where .
The proper acceleration of a particle is determined as if the photon is generated in a quantum region, with size [8].
Considering that (equivalent mass of a photon) and , and in addition taking care of the uncertainty principle for momentum , and energy , then the proper acceleration of the photon is estimated [9]:
When we let , we obtain wave functions for subluminal speed as [10] ( ):
and for superluminal speed ( ):
Where is an angular frequency of the particle and is the ratio of the particle velocity divided by the light speed.
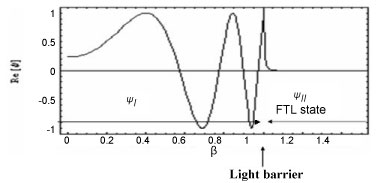
Figure 1 shows the wave function for the highly accelerated particle, which shows the possibility of tunnelling through the light barrier.
If we consider the light barrier as a potential barrier, the probability of a particle to tunnel through the light barrier can be estimated in the WKB approximation and it is given by
Supposing that the size of the quantum region is approximately equal to the Plank length , we have
Obtained after inserting , a value that can be estimated from the uncertainty principle [11].
Then Equation (8) can be rewritten under the form
Where
and
Probability of a Photon to Tunnel through the Light Barrier
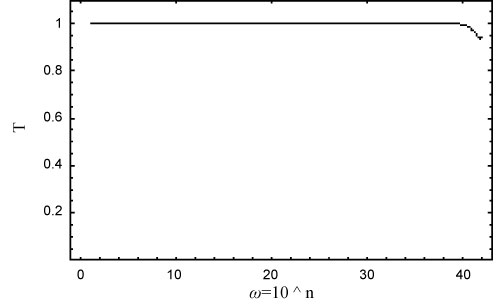
From Equation (9), we can estimate the probability of a photon to tunnel through the light barrier, represented graphically in Figure 2. In this figure, the horizontal line is for the radial frequency of the photon and the vertical line is for the probability of photons to tunnel through the light barrier.
From this figure, the probability of a photon in a superluminal state almost becomes unity up to the Plank frequency ( Hz), and it is seen that the photon is generated as a superluminal particle. From Figure 1, it can be seen that a tunneling particle through the light barrier returns to the original state within a finite length of time, which can be estimated by the uncertainty principle. The difference of momentum of the photon in an original state at the source and the photon in a superluminal state can be estimated to be , where p is the momentum of the photon in a superluminal state. As the momentum of the photon can be described as , then from the uncertainty principle, , we get
Which represents the traveling distance of a photon in a superluminal state.
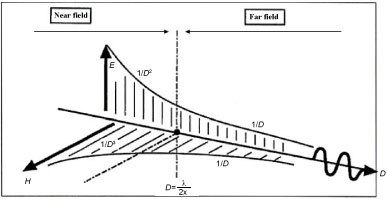
This value coincides with the region of the near field of the electromagnetic wave as shown in Figure 3 and we can conclude that photons moves in a near field from the source at the superluminal speed and reduce to the speed of light (i.e. group velocity of the light wave) as they propagate into the far field.
W. D. Walkers obtained the same result for the electromagnetic wave by using the electromagnetic theory [12-14], and he claimed that it should be possible to reduce the time delay by monitoring lower frequency EM field in the electromagnetic near-field.
Conclusion
From the above theoretical analysis, it is seen that photons propagate at superluminal speed in the electromagnetic near-field from the source and reduce to the speed of light as they propagate into the far field. This phenomenon can be applied for speeding up the processing time of photonic computer systems.
Acknowledgement
The author appreciates Prof. Mario J. Pinheiro at University of Lisbon (IST) to help him to revise this paper.
References
- Recami E (2001) A bird's-eye view of the experimental status-of-the-art for superlsuminal motions. Foundation of Physics 32: 1119-1135.
- Brown J (1995) Faster than the speed of light. New Scientist 146: 26-30.
- Steinberg AM, Kwait PG, Chiao RY (1993) Measurement of the single-photon tunneling time. Physical Review Letters 71: 708-711.
- Wang LJ, Kuzmich A, Dogariu A (2000) Gain-assisted superluminal light propagation. Nature 406: 277-279.
- Caligiuri LM, Musha T (2014) Quantum vacuum dynamics, coherence, superluminal photons and hypercomputation in brain microtubules. Applied Numerical Mathematics and Scientific Computation 105-115.
- Musha T (1998) Possible existence of faster-than-light phenomena for highly accelerated elementary particles. Speculations in Science and Technology 21: 29-36.
- Musha T (2005) Superluminal effect for quantum computation that utilizes tunneling photons. Physics Essays 18: 525-529.
- Jyukov AI (1961) Introduction to the theory of relativity. National Culture Physics Mathematics Library, Moscow.
- Caianiello ER (1984) Maximal acceleration as a consequence of Heisenberg's uncertainty relations. Lettere Al Nuovo Cimento 41: 370-372.
- Musha T (2009) Thermal radiation generated inside the Sun due to the Cherenkov radiation from ZPF field. Far East Journal of Applied Mathematics 37: 229-235.
- Musha T (2001) Cherenkov radiation from faster-than-light photons created in a ZPF background. Journal of Theoretics 3.
- Walker WD (2000) Experimental evidence of near field superluminally propagating electromagnetic fields. Viger III Symposium "Gravitation and Cosmology", Berkley, California, USA, 21-25.
- Walker WD (1999) Superluminal near-field dipole electromagnetic fields. International Workshop Lorentz Group CPT and Neutrinos, World Scientific, Zacatecas, Mexico.
- Walkers WD (1998) Superluminal propagation speed of longitudinally oscillating electrical fields. Conference on Causality and Locality in Modern Physics, Toronto, Canada.
Corresponding Author
Takaaki Musham, Advanced Science-Technology Research Organization, Yokohama, Japan.
Copyright
© 2019 Musha T. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.