Development of Whispering Gallery Mode Polymeric Micro-optical Sensors to Detect Chemical Impurities in Water Environment
Abstract
In this paper, we develop dielectric micro-optical sensors based on Whispering Gallery Mode Phenomenon (WGM) for monitoring of chemical impurities in contaminated drinking water environments. Some sort of chemical impurities could be toxic and carcinogenic to humans and animals. The biogeochemical reactions are governing the chance and the movement of these impurities in the drinking water environment. Based on that, it is important to measure and quantify the concentration of these impurities in the water medium. In the present paper, a high-resolution micro-optical sensor concept is used to detect these chemical impurities. The sensing element is a silica microsphere acts as an optical resonator. The proposed sensor aims to provide preliminary results demonstrating the practical use of these sensors for effective monitoring of chemical impurities concentrations and contaminants such as sodium phosphate which can cause serious kidney damage and possibly death. Results indicate that the WGM based-sensors are sensitive enough to refractive index changes in the case of liquid media (water). Experiments were carried out to validate the analysis and to provide an assessment of this sensor concept. Results indicate sensor resolutions of ∼0.0299 μm for sodium phosphate using this approach.
Keywords
Optical resonators, Whispering gallery modes, Chemical impurities, Sodium phosphate, Index of refraction
Introduction
Recently, optical microsphere resonators have sparked interest due to their high quality factors. The quality factor, Q, is a measure of the resolution of the optical resonance, also known as the whispering gallery mode (WGM), of the sphere. Q is defined as, Q = λ/δλ, where λ is the wavelength of the laser and δλ is the resonance line width. There are reported Q values approaching a material loss limit of 1010 [1]. It is these extremely high Q values that provide the opportunity for detection of very small morphology dependent shifts in micro spherical sensor's whispering gallery modes. A current method of measuring the extremely high Q factors is by coupling a laser into a micro-spherical resonator tangentially using tapered single optical fibers [2]. To avoid any fluctuation in the spectrum due to any disturbance between the fiber and the sphere we recommend making the fiber mechanically touching the sphere to make the overall system stable. These morphological changes can result from changing stimuli in the environment and provides for a range of new sensor development opportunities. By monitoring the effects of the stimuli on the microsphere WGM, it is possible to determine the corresponding physical state of the surrounding environment. These unique characteristics of micro-spherical resonators have been used in multiple biological and mechanical sensing applications including but not limited to: laser frequency locking and stabilization, micro cavity laser technology, optical communications (switching, filtering and multiplexing [3-5] and sensor technologies in temperature measurement [6], mechanical forces measurement [7], electric field detection [8,9], angular velocity measurement [10] and biological applications [11].
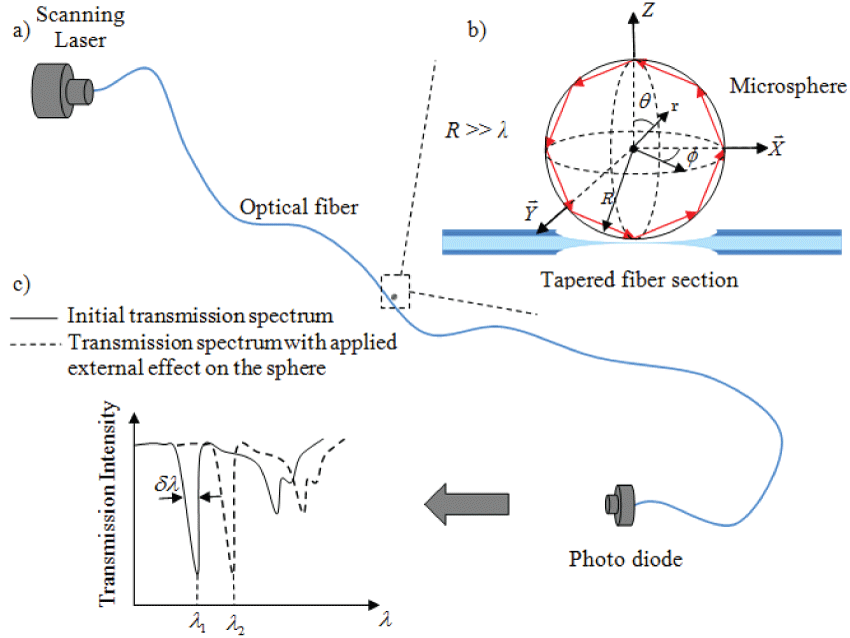
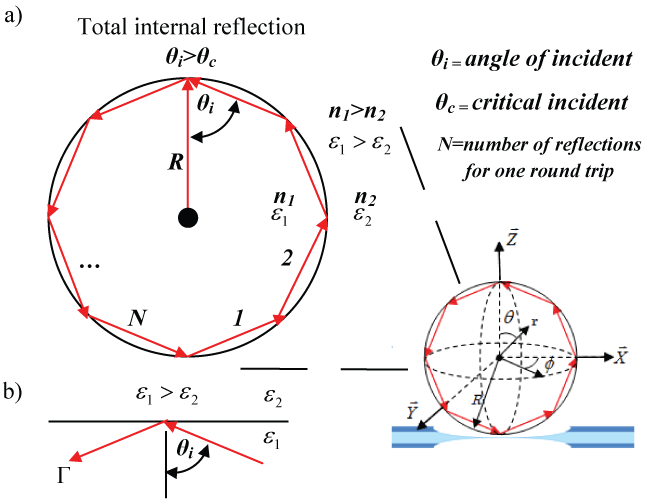
The simplest interpretation of the WGM phenomenon comes from geometric optics. When laser light is coupled into the sphere nearly tangentially (Figure 1a), it circumnavigates along the interior surface of the sphere through total internal reflection.
An optical resonance is realized when light returns to its starting location in phase. A common method to excite WGMs of spheres is by coupling tunable laser light into the sphere via an optical fiber. The approximate condition for resonance is
Where R and n1 are the sphere radius and refractive index respectively, λ is the vacuum wavelength of the light, and l is an integer indicating the circumferential mode number. Equation 1 is a first order approximation and holds for R >> λ (Figure 1b). At resonance, light experiences constructive interference in the sphere which is observed as dips in the transmission spectrum through the optical fiber (Figure 1c). A fractional change in the index of refraction or the radius will induce a shift in the WGM as
Equation 1 is an approximation that helps us evaluate the first order effects on WGMs of the sphere those due to a change in R or n1. However, each time the light is reflected off the inner surface of the sphere, the reflected wave experiences a certain "phase delay". This phase delay is a function of the light wavelength, λ, incidence angle, θi as well as the sphere-to-surrounding refraction index ratio, n1/n2.Therefore, for a given laser wavelength and coupling angle, the total optical path length for the round trip of the light is somewhat different from 2πRn1 and is a function of the refractive index of the surrounding medium, n2. By tracking the WGM shifts induced by perturbations in n2, the surrounding medium can be monitored provided that the induced shifts are in the order of dλ or larger. In this paper we will keep tracking the WGM shifts due to the change of n2 because of sodium phosphate. However, n2 changes also affect the quality factor, Q and hence dλ. In the analysis section in this paper the effect of n2 on the WGM resonance is analyzed using a simple geometric optics and basic electromagnetic equations.
Figure 2 depicts the geometric optics view of the WGM resonance condition. In this view, the laser light circles the interior of the sphere through multiples of total internal reflections and returns in phase. The approximate condition for optical resonance or WGM is equation 1 satisfied.
Experimental Investigation
Sensing element fabrication
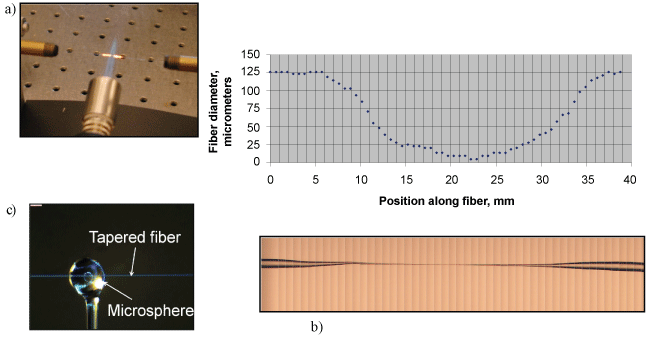
To prepare the cavity for that function the evanescent field outside the fiber needs to be extended, in order to achieve efficient optical coupling between the micro-optical cavity and the fiber. This can be achieved by first removing the outermost protective buffer layer and then heating and stretching a portion of the fiber (with both the cladding and core) to create a tapered section with a minimum waist of 10 to 20 μm as seen in Figure 3a, Figure 3b respectively. A micro-torch is used in the present work to prepare a tapered section of the fiber. A micro-torch is used in the present work to prepare a tapered section of the fiber as was done in our previous studies [7,12-14].
Optical cavity is manufactured using a ~5 cm long piece of optical fiber which is first stripped of its plastic cladding using an optical stripper and then heated and stretched to provide a stem end (with a tip diameter of ~60 μm). The tip of this silica fiber is then melted under high temperature using a torch to form a cavity at the end of the stem as shown in (Figure 3c).
Figure 4, shows laser light is coupled to the cavity using the tapered fiber.
Optoelectronics setup
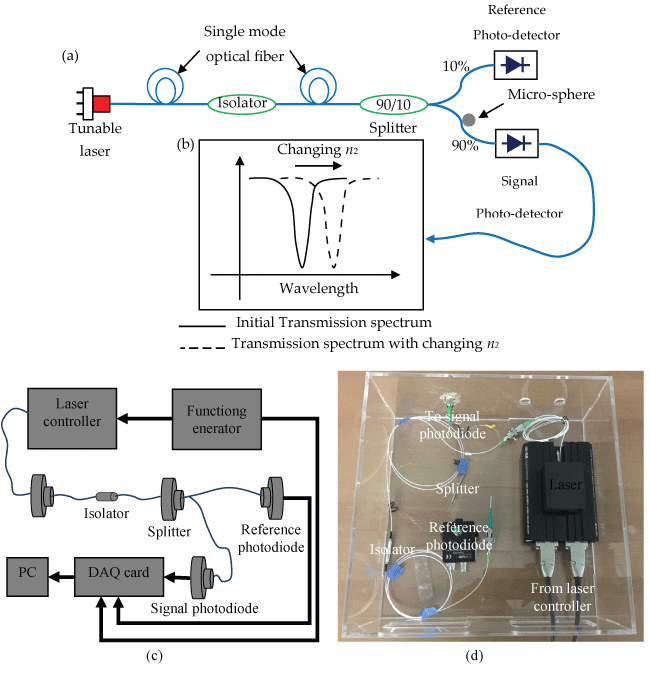
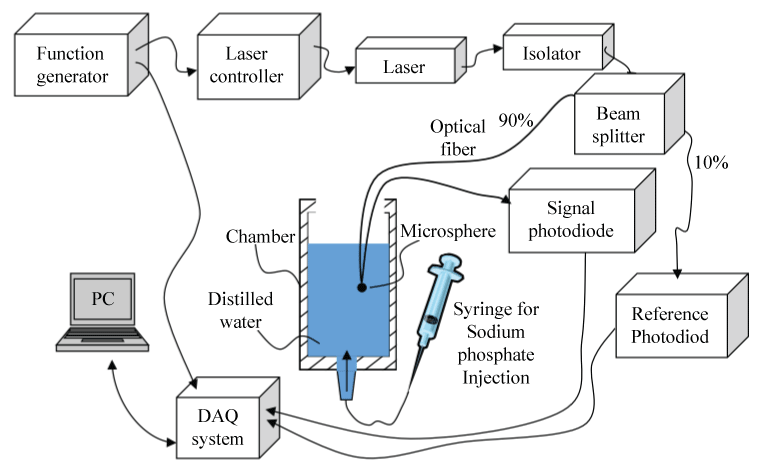
Figure 5 shows a schematic, block diagram and photograph of the optoelectronics setup for the proposed sensor design. The function generator supplies the tuning waveform to the laser controller which, thus, presents the same waveform in electrical current to the laser to modulate its wavelength. The laser output is coupled right into a single mode optical fiber which is cut up into two; one side is coupled to the sensor resonator (in the present, a micro-cavity) supplying the transmission spectra at the same time the other (with ~10% of the total intensity) is used as a reference signal. Every fiber is ended into a photograph diode as demonstrated. Both the transmission spectra and the reference signal are sampled utilizing a 16-bit analog-to-digital converter and processed by a host machine. The reference is utilized to normalize the transmission spectra. A software module, created in-house, investigates the normalized transmission spectra to monitor the WGM shifts.
The change in the surrounding medium of the cavity due to the change of the n2 can cause change in the optical cavity and then it's WGM. A tapered optical fiber is used to couple the IR tunable laser where the WGM would see as a sharp dips on the transmission spectrum as shown in (Figure 5).
Experimental procedures
The output of the tunable distributed feedback laser diode was coupled into a single mode optical fiber with core diameter of ~9 μm and cladding of 125 μm. The laser beam is split in two by a beam splitter 90% and 10% so that the 10% of the beam intensity goes to a photodiode to monitor the laser beam intensity and use it as a reference signal. The fiber with the 90% intensity was sent to the "sensor" side of the fiber with the microsphere in contact with it. At its output end, this fiber is connected to a fast photodiode to monitor the transmission spectrum. This signal through the sensor fiber was normalized using the reference signal. The microsphere was brought very close to the tapered fiber at a distance of the order of several nanometers to facilitate good light coupling between fiber and resonator. The laser is tuned by ramping the current into it using a laser controller. The controller, in turn, was driven by a function generator that provided a saw-tooth input to the controller. The output of both photodiode was monitored by 16 bit digitizer data acquisition card that was part of a host PC. The sphere diameters ranged between 100 ± 50 and 500 ± 50 μm in the present experiments.
The details of the test section are shown in (Figure 6). In these experiments, the effect of sodium phosphate concentration in water on the WGM shifts is studied. The micro-sphere is placed in deionized water in a container. A sodium phosphate solution was gradually added to the container and allowed to diffuse for uniform concentration before the WGM shifts are observed. The temperature of the solution was monitored by a thermocouple and kept a constant value of 25 °C. The transmission spectrum was digitized and stored on the host PC to determine the WGM shift. The measurements were repeated with increasing concentrations of the solution.
Analysis Investigation
Starting with a quantum analogy-based theory developed by Johnson [15] describing the optical resonances of a sphere, Teraoka, et al. [16] carried out a perturbation approach to study WGM shifts due to changes in the refractive index of the medium surrounding the sphere. More recently, Schweiger and Horn [17] used a wave theory approach to obtain similar results. We present here a simple approach using geometric optics, along with basic electromagnetic wave reflection expressions, to obtain equations that accurately describe the resonant wave number k1 and quality factor Q of the WGM. That is, using simple physical modeling of reflections at an interface, we derive a modified version of equation 1, together with an expression for the associated Q, in which the effect of n2 is included. The analysis is valid for R >> λ and the sphere is treated as a cylinder for conceptual simplicity with the light traveling on a plane parallel to the end surfaces of the cylinder. When the order number λ of resonance is large, the cylindrical resonance condition would accurately model a spherical resonance as well. The analysis yields two distinct equations for the transverse electric (TE) and transverse magnetic (TM) modes.
Consider the reflection of a plane wave from a dielectric interface, as shown in Figure 2b, when the angle of incidence θi is larger than the critical angle. That is
Where n and are the refractive indices and the dielectric constants of the resonator (1) and surrounding media (2). The reflection from such a planar interface should accurately model each individual reflection in the ray optics description shown in Figure 2a. The reflection coefficients ΓTE and ΓTM for the TE and TM polarizations are expressed using equivalent impedances of the two media as [18]
Where,
and,
With Z0 = 377 Ω as the wave impedance of free space. Our interest is the phase associated with each reflection coefficient for large N.
Combining equations 4 and 5 for the TE polarization,
Referring to Figure 2a, we note that, for N >> 1, the incidence angle θi is given by
Therefore, arg (ΓTE) can be approximated as follows:
Similarly, combining equations 4 and 6 for the TM polarization,
Yielding the argument
Again, Equation 12 can be approximated using equation 9
Equation 10 shows that the reflection phase is close to π for the TE mode. We also know that the magnitude of reflection is unity (total internal reflection). Therefore, we may consider the case as a perturbation of an ideal conducting wall for which |Γ| = 1 and arg (Γ) = π. Accordingly, the TE resonant condition for the dielectric sphere of Figure 2a may also be considered as a perturbation of that for a sphere with an ideal conducting wall. Using multiple ray-reflection model shown in Figure 2a, we consider the resonant condition for the conducting sphere first. The resonance radius is analytically known from the first zero of the lth order Bessel function [18,19] that is k1R ≈ l + 1.856l1/3. Here, k1 = 2π/λ is the wave number and λ is the wavelength in the sphere. Thus, from Figure 2a and using equation 9, the resonant condition can
The factor 1.856l1/3 in the equation (14) can be interpreted as a first order correction that accounts for the spherical nature of the wave front and the curvature of the resonator boundary, which is different from the simple plane wave treatment. For large mode numbers (l >> 1) this term would be small compared to l, resulting in the approximate resonance condition of equation 1. The resonant condition for the dielectric cavity of Figure 2a may now be determined by including in equation (14) and the phase contribution of equation 10
Note that the final resonant condition does not depend on N, which is the number of reflections the light ray experiences for one full round trip in sphere as shown in Figure 2a. Also, in principle, N need not be an integer.
The change in the resonant condition due to an incremental change in n2 can be evaluated by differentiating equation 16.
or,
Where
The treatment for the TE polarization presented above can be repeated for the TM polarization, noting only the key differences. From equation 13 we see that reflection phase for TM polarization is close to zero for large N. Therefore, the resonant dielectric sphere of Figure 2a may be considered as a perturbation of a sphere with an ideal magnetic wall for which |Γ| = 1 and arg (Γ) = 0. As in the TE resonance case, the TM resonant radius for the magnetic-walled resonator would also correspond to the first zero of the lth order Bessel function [18,19] with k1R ≈ l + 1.856l1/3. So we have.
The above equation is the TM counterpart of equation 16. Again, the resonance shifts due to an incremental change in the refractive index of the surrounding medium can be obtained by differentiating equation 20
or,
Equations 18 and 22 describe the dependence of the resonant frequency WGM shift on the refractive index of the medium surrounding the sphere for TE and TM polarizations, respectively. Note that l is kept constant in obtaining the above derivatives. In an earlier study, Teraoka, et al. [16] carried out a perturbation analysis based on an equivalent quantum theory model of the optical modes of spheres [15] to obtain expressions describing WGM dependence on Δn2. For k0R1 >> 1, equation 17 and the implicit formula obtained by [16] differs by the ratio of . However, when the order number is approximated by l = n1k0R their expression for WGM shift becomes identical to equation 17.
The resonance analysis presented above models the interface between the microsphere and the external medium (Figure 2a) as a planar surface (Figure 2b). This results in total internal reflection, with magnitudes of the reflection coefficients equal to unity. However, each reflection generates some radiation, attributed to the curvature of the interface. We model the radiation loss with an equivalent radiation resistance Rre and Rrm, for TE and TM polarizations, respectively. The reflection coefficients for the TE and TM modes, taking into account the equivalent radiation resistance are given as
The impedances ZTE1, ZTE2, ZTM1, and ZTM2 are given by equations 5 and 6.
The WGM shifts are sensitive to the refractive index changes in the case of liquid media (water). Using k = 2π/λ,
Equations 19 and 23 can be rewritten in terms of wavelength, λ for the TE as;
or
Results and Discussion
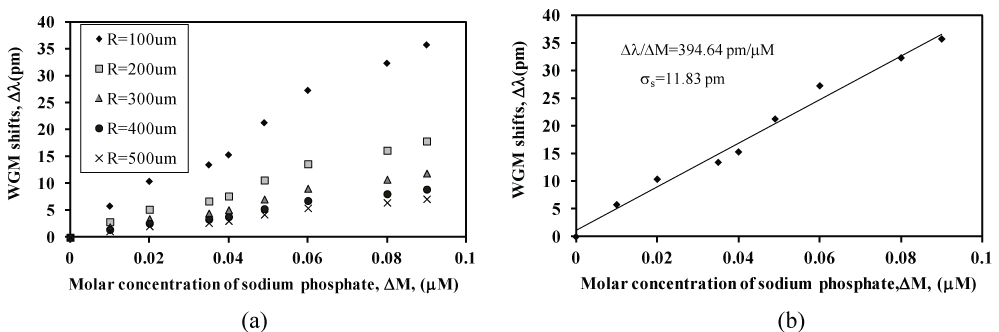
Figure 7 shows the WGM shift of the micro sphere under the effect of different sodium phosphate concentrations up to 0.1 μM concentration. The measurements were repeated using silica microspheres with five different radii ranged from (100 ± 50 μm, to 500 ± 50 μm) as shown in Figure 7a. The corresponding sensitivity plot of WGM shift vs. phosphate concentrations for the sensor with radius 100 ± 50 μm is presented in (Figure 7b). The best fit of the data (solid line) indicates a sensitivity of = 394.64 pm/μM. The corresponding resolution limit for this optical method is (ΔM/Δλ)σs = 0.0299 μM. In this case, the standard deviation (σs) of the data scatter was σs = 11.83 pm. The change in the index of refractive index Δn2 can be determined based on equation 25.
The amount of phosphate in the environment strongly influences the operations of living organisms. The excess amount of phosphate is an indicator for possible problematic algal growth in rivers [20]. In contrast, low phosphate concentration causes death of vegetation since plants utilize the inorganic phosphate for photosynthesis, respiration, and the regulation of enzymes [21]. Since phosphate plays an important role in the soil and groundwater sediments both for uranium and living organisms as well as to ensure consistent water quality, the phosphate concentration should be quantified and monitored in order to deploy the right quantity for remediation. Throughout the years, these factors encouraged the scientists to investigate methods for phosphate detection [22-29]. Up to now, several sensor technologies for monitoring phosphate species have been implemented. Table 1 summarizes the resolution limits of phosphate from various techniques. In this paper we show that our new optical technique will be able to measure up to 0.0299 μM. Also, our optical technique will enhance and improve the sensitivity level for the sodium phosphate impurities in water compared to the published works of sodium phosphate sensors as shown in (Table 1).
Conclusion
In this paper, a simple ray tracing, plane wave approach used in the present analysis results in equations for dependence on n2. An optical chemical impurities sensor based on the whispering gallery modes of spherical resonators has been demonstrated. The preliminary data of the newly developed biosensor promises more accurate and sensitive for sodium phosphate for water treatment. So far, we have measured up to 0.0299 μM phosphate concentrations in the water via employing newly developed optical sensor based on WGM. Since the research is still underway, we are targeting to lower the phosphate detection limits as well as to test their field application capacity. According to the literature, the stability of the multi enzyme-linked sensors depends upon the life-span of the enzyme. In order to increase the durability of the sensor, the single enzyme technology was chosen to develop the phosphate sensing system based on the same optical technique that we presented in this paper.
References
- Jonáš Alexander, Karadog Yasin, Mestre Michael, et al. (2012) Probing of ultrahigh optical Q-factors of individual liquid microdroplets on superhydrophobic surfaces using tapered optical fiber waveguides. Journal of the Optical Society of America B 29: 3240-3247.
- Offrein BJ, Roland Germann, Horst F, et al. (1999) Resonant coupler-based tunable add-after-drop filter in silicon-oxynitride technology for WDM networks. IEEE J Sel Top Quantum Electron 5: 1400-1406.
- Ilchenko VS, Volikov PS, Velichansky VL, et al. (1998) Strain tunable high-Q optical microsphere resonator. Opt Commun 145: 86-90.
- Tapalian HC, Laine JP, Lane PA (2002) Thermo optical switches using coated microsphere resonators. IEEE Photon Technol Lett 14: 1118-1120.
- Little BE, Chu ST, Haus HA, et al. (1997) Microring resonator channel dropping filters. J of Lightwave Technol 16: 998-1005.
- Guan Guoming, Arnold Stephen, Ötügen MV (2006) Temperature Measurements Using a Micro-Optical Sensor Based on Whispering Gallery Modes. AIAA Journal 44: 2385-2389.
- Ioppolo T, Kozhevnikov M, Stepaniuk V, et al. (2008) Micro-optical force sensor concept based on whispering gallery mode resonances. Appl Opt 47: 3009-3014.
- Amir R Ali, Ioppolo Tindaro, Ötügen MV (2013) Beam-coupled microsphere resonators for high-resolution electric field sensing. Proc. SPIE 8600, Laser Resonators, Microresonators, and Beam Control XV, 86001R.
- Amir R Ali, Ioppolo T, Ötügen MV (2012) High-resolution electric field sensor based on whispering gallery modes of a beam-coupled dielectric resonator. Engineering and Technology (ICET).
- Ali AR, Ioppolo T (2014) Effect of Angular Velocity on Sensors Based on Morphology Dependent Resonances. Sensors 14: 7041-7048.
- Vollmer F, Braun D, Libchaber A (2002) Protein detection by optical shift of a resonant microcavity. Appl Phys Lett 80: 4057.
- Ioppolo T, Ayaz UK, Ötügen MV (2009) High-resolution force sensor based on morphology dependent optical resonances of polymeric spheres. J Appl Phys 105.
- Ioppolo Tindaro, Ötügen Volkan (2007) Pressure tuning of whispering gallery mode resonators. J Opt Soc Am B 24: 2721-2726.
- Ioppolo T, Ayaz U, Ötügen MV (2009) Tuning of whispering gallery modes of spherical resonators using an external electric field. Opt Express 17: 16465-16479.
- Johnson BR (1993) Theory of morphology-dependent resonances: shape resonances and width formulas. J Opt Soc Am A 10: 343-352.
- Teraoka Iwao, Arnold Stephen, Frank Vollmer (2003) Perturbation approach to resonance shifts of whispering-gallery modes in a dielectric microsphere as a probe of a surrounding medium. J Opt Soc Am B 20: 1937-1946.
- Gustav Schweiger, Marion Horn (2006) Effect of changes in size and index of refraction on the resonance wavelength of microspheres. J Opt Soc Am B 23: 212-217.
- Roger F Harrington (2001) Time-Harmonic Electromagnetic Fields. Wiley Interscience-IEEE, New York.
- Abramowitz Milton, Stegun IA (1965) Handbook of Mathematical Functions.
- O'Toole Martina, Lau Kim, Shepherd Roderick, et al. (2007) Determination of phosphate using a highly sensitive paired emitter-detector diode photometric flow detector. Analytica Chemica Acta 597: 290-294.
- Raghothama KG (1999) Phosphate Acquisition Annual Review of Plant Physiology and Plant Molecular Biology. 50: 665-693.
- Parra A, Ramon M, Alonso J, et al. (2005) Flow Injection Potentiometric System for the Simultaneous Determination of Inositol Phosphates and Phosphate: Phosphorus Nutritional Evaluation on Seeds and Grains. J Agric Food Chem 53: 7644-7648.
- Quintana JC, Idrissi L, Palleschi G, et al. (2004) Investigation of amperometric detection of phosphate Application in seawater and cyanobacterial biofilm samples. Talanta 63: 567-574.
- Akyilmaz Ero, Yorganci Emine (2007) Construction of an amperometric pyruvate oxide enzyme electrode for determination of pyruvate and phosphate. Electrochim Acta 52: 7972-7977.
- Kwan RC, Leung HF, Hon PYT, et al. (2005) A screen-printed biosensor using pyruvate oxidase for rapid determination of phosphate in synthetic waste water. Appl Microbiol Biotech 66: 377-383.
- SY Chang, Wei-Lung Tseng, S Mallipattu, et al. (2005) Determination of small phosphorus-containing compounds by capillary electrophoresis. Talanta 66: 411-421.
- Nakashima Y, Goto T, Kitazumi I, et al. (2001) Capillary electrophoretic determination of phosphate based on the formation of a Keggin-type [PMo12O40]3−complex. Electrophoresis 22: 3377-3381.
- Axel Durkop, Turel Matejka, Aleksandra Lobnik, et al. (2006) Microtiter plate assay for phosphate using a europium-tetracycline complex as a sensitive luminescent probe. Anal Chim Acta 555: 292-298.
- Lin X, Wu X, Xie Z, et al. (2006) PVC Matrix Membrane Sensor for Fluorescent Determination of Phosphate. Talanta 70: 32-36.
Corresponding Author
Amir R Ali, Mechanical Engineering Department, Southern Methodist University, USA; Mechatronics Engineering Department, German University in Cairo, Egypt, Tel: +20-122-225-7086.
Copyright
© 2017 Ali AR. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.