Extremely-Consistent Dielectric Capacitors with Excellent Comprehensive Dielectric Permittivity Characteristics Using (Ba, Sr) (Ti, Zr) O₃ Lead-Free Ceramic-Based Relaxor Ferroelectrics

Abstract

For decades, lead-free eco-friendly BaTiO ₃ ferroelectric materials and their derivate are established to be exceptional candidates for maintainable development and piezoelectric devices. In this work, the lead-free Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ system is prepared using a conventional solid-state reaction method. The incorporation of the Sr and Zr elements into the BaTiO ₃ matrix has broken the long-range ferroelectric polarization to announce the formation of Polar Nano-Regions (PNRs). The structural results have confirmed that the Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ reveals a single phase with a P4mm space group. The Raman analysis indicates the presence of active vibration Raman modes Ґ _{R3c, Raman} = 9A ₁ +9E. Moreover, both the X-ray diffraction (XRD) study and Raman results approve the absence of secondary phases. The temperature-dependent permittivity shows the presence of broad and frequency-dependent maximum dielectric pics. At 100 Hz, the maximum value of the relative permittivity ε′ ≈ 7000 is higher than that for conventional BaTiO ₃ perovskites (ε′ = 3000-6000). These results are due to the existence of PNRs in Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ and the lattice distortion effects in high entropy systems. The evolution of the characteristic frequency versus the maximum temperature is discussed in terms of the Vogel-Fulcher equation. Likewise, the characteristic diffuseness of the dielectric peak is described based on an empirical Lorenz-type relation. The deviation from the Curie-Weiss law (γ = 1.623) indicates that the lead-free Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ ferroelectric compound reveals a relaxor behavior. The encouraging dielectric properties (elevated relative permittivity of ε′ ≈ 7000 and very low dielectric losses of tan (δ) = 0.1) establish a basis for the application of Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ in capacitor devices due to the high-performance dielectric energy storage of the prepared lead-free perovskite.

Keywords

Relaxor, Ferroelectrics, Dielectric properties, PNRs

Introduction

Due to the attractive physical properties of the oxide materials, perovskites offer multipurpose functionalities and are talented systems for numerous applications to spintronic, electronic, solar cells, and sensors devices [1-7]. In addition, perovskites with switchable spontaneous polarization have occupied a main position as nonlinear optical systems, of which birefringence is a critical merit to optical devices. Moreover, multifunctional perovskites remain an excessive challenge to tune and control their birefringence, therefore hindering the usefulness of oxides in optical domains [3-6]. According to recent investigations, it has been observed that perovskites display exceptional dielectric, and simultaneously multiferroic behaviors [7-10]. Therefore, a variety of multiferroic systems like lead-free compounds have been extensively employed as capacitors, motors, sensors, surface acoustic wave devices, actuators, and energy storage applications [2].

Over the past century, it has been shown that the physical properties of perovskites are influenced by numerous parameters like the microstructure (size and shape of their particles) [1-5]. Among multiferroic structures, lead-free titanate ceramics (PbTiO ₃ , SrTiO ₃ , BaTiO ₃ …) are the subject matter of various experimental and theoretical investigations due to the strong interplay between its physical properties [2-7]. This material family is mentioned by a ferroelectric character with diffuse phase transition [11-21]. Lead-based perovskites such as PbTiO ₃ and Pb(Mg, Nb)O ₃ have shown a great relaxor behavior and the Burns temperature (T _B ) at about 300 °C [22]. This makes the titanate systems a good candidate for the design of transducers and storage devices [1-8]. In addition, multiferroic ceramics can be used as precision actors in the optical system, and ferroelectric random memories [9-19].

Since then, most of the recent researches on dielectric capacitors devices are focused to improve the dielectric characteristics of BaTiO ₃ . Accordingly, it is shown that the aforementioned system and their derivate reveal higher dielectric permittivity and lower energy storage density that permits the use of lead-free perovskites for technological applications for instance capacitors. Moreover, BaTiO ₃ is characterized by better chemical stability since it does not cover volatile elements. BaTiO ₃ materials have unusual characteristics related to dipolar relaxation manifesting by frequency-dependent dielectric peak temperature. Dipolar relaxation has commonly been explicated by the existence of Polar Nano Regions (PNRs), which are improved by the so-called Burns temperature T _B [20,21]. Compared with the toxic PbTiO ₃ and PbMgNbO ₃ systems, BaTiO ₃ is among the most environmentally friendly systems. Those compounds reveal excellent ferroelectric and piezoelectric characteristics. Recently, it has been reported that BaTiO ₃ perovskites reveal a characteristic Curie temperature between 120 °C and 130 °C depending essentially on the grain size, porosity, and chemical composition. According to numerous investigations, impurities, sintering times, oxygen stoichiometry, carrier density, thermal velocity, and microstructural features (crystallite size and crystallite size distribution) are the responsible factors that determine the dielectric properties of lead-free systems. Moreover, the cationic disorder factor plays a significant role in electron transfers, dielectric permittivity and dielectric loss responses.

To enhance the energy storage properties of titanate compounds, the greatest common means is to modify BaTiO ₃ -based systems from normal ferroelectric to relaxor ferroelectric by combing with other ceramics, like SrTiO ₃ and BaZrO ₃ ferroelectric systems. Accordingly, the dielectric properties of BaTiO ₃ ceramic depend mainly on the co-doping, as well as the substitution in both Ba and Ti sites. For instance, it has been reported that doped with Sr ²⁺ cations at the Ba ³⁺ -site and the substitution at the Ti-site with Zr element affects the mixed-valence state of the transition metal element, which modifies the double exchange process. Investigations on substituted BaZrTiO ₃ have shown the variation in structural, electrical, and dielectric optical band-gap properties of the ceramic. An enhancement in piezoelectric coefficient has been remarked on versus the substation by Sr and Zr elements at Ba-site and Zr-site in BaTiO ₃ . Furthermore, the substitution of lead-free BaTiO ₃ touches the optical gap energy. Zr doping in BaTiO ₃ has gained great consideration as an imperative ferroelectric compound.

This paper reports a study of the relaxor behavior of the lead-free Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ ferroelectric material. A significant level of chemical substitution in Barium titanate BaTiO ₃ -based relaxors seems to be the best way to tune the crystal structure and dielectric properties. X-Ray diffraction and Raman Spectroscopy are done to reveal the effect of substitutions on the Ba and Ti sites of the perovskite. Then, a dielectric study confirms the correlation between all results. Additionally, the dielectric results indicate that the prepared ceramic exhibits elevated relative permittivity of ε′ ≈ 7000 and very low dielectric losses of tan (δ) = 0.1) that establish the basis for the application of Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ in capacitor devices.

Materials and Methods

Polycrystalline relaxor Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ is synthesized using a conventional route based on the solid-state reaction method. The raw powders BaCO ₃ , SrCO ₃ , TiO ₂ , and ZrO ₂ are weighed according to the stoichiometric formula, mixed, and milled by adding an amount of ethanol (valued at 10%) using an agate mortar. The obtained powder is calcined for 15 hours at 1150 °C with a heating rate of 5 °C/min. The calcined pellet is mixed with an aqueous polyvinyl-alcohol (PVA) solution, dried at 80 °C for 1 hour, mixed again, and pressed into disk-shaped pellets of 8 mm diameter using a hydraulic press under uniaxial pressure of 1000 Pa. Evaporation step of PVA is effectuated with thermal treatment at 600 °C for 4 hours. Finally, the obtained pellet is sintered in air at 1470 °C for 4 hours with a heating rate of 5 °C/min.

The phase analysis is characterized, at room temperature, using a powder diffractometer Bruker D8 Advance. Accordingly, the X-ray diffraction (XRD) pattern has been recorded using kα ₁ radiation from the Cu anode in a range of 2θ between 20° and 80° with a step size of 0.009°. Profile pattern adjustment is performed using FULLPROF Software.

Scanning electron microscopy (SEM) analysis has been obtained on FEI Quanta 200 equipment operated at 15 keV. The SEM analysis aims to investigate the internal morphology and examine the microstructure of the prepared ceramic sample. The transmission electron microscopy (TEM) analysis of Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ is obtained using high-resolution transmission electron microscopy (HRTEM) in a Tecnai G2.

To conduct the TEM studies, the prepared powder is crushed in ethanol. After that, some drops of the obtained solution are dispensed on a copper grid covered by a holey-carbon film. To obtain additional information about the structural symmetry groups with a nondestructive probe, scattering Raman spectra are verified with a LABRAMHR800-Yvon Jobin T64000 triple grating spectroscopic system. The ceramic is excited with a 514.5 nm line of an Ar laser at a power of 100 mW (~25 mW on the sample). To control the temperature variation from -130 °C to 200 °C, ATHMS-E600 Linkam Scientific Instrument is used. Spectra are measured using the natural polarization of the green laser and corrected for the instrumental function of the microscope. Then, the spectra are temperature reduced to account for the Bose-Einstein phonon occupation factor deconvoluted into Pseudo-Voight function PV = q × L+ (1-q) G: L, and G are Lorentzian and Gaussian functions and q is a weight coefficient that determines the peak positions. The frequency-dependent complex dielectric constant ε ^* (f, T) = ε’-i ε” of the prepared compound is measured between -130 °C and 200 °C and over a large frequency range from 100 Hz to 10 kHz. The sample with a diameter of 6.86 mm and thickness of 0.88 mm is coated using silver paint as an electrode. The dielectric properties are obtained using a Solartron SI1260 impedance analyzer coupled with a full computer. The amplitude of the probing ac electric signal is 1 V/mm. The dielectric data are collected every 2 °C, keeping a heating rate of 5 °C/min.

Results and Discussions

Structural study

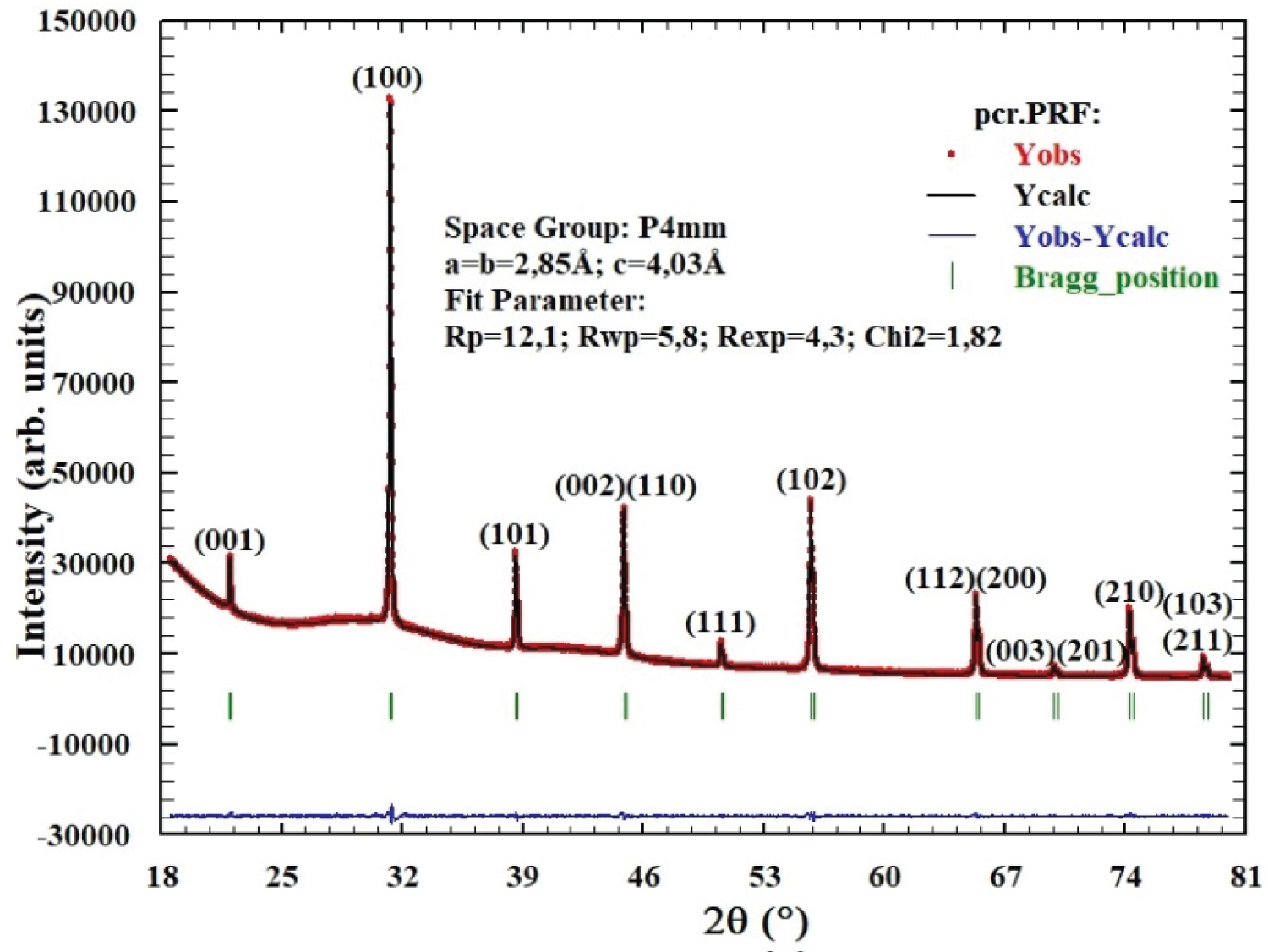
Figure 1 shows the X-ray diffraction (XRD) characterization and the fitted patterns, using FULLPROF software, for the prepared Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ (BSTZ) perovskite. According to the obtained results, all the diffraction peaks are indexed in a tetragonal symmetry compatible with the P4mm (No. 99) space group . Moreover, the profile-matching refinement analysis has confirmed that the prepared ceramic reveals a high degree of crystallinity. Accordingly, the obtained unit cell data for the BSTZ ceramic are a = b = 2.85 Å, and c = 4.03 Å [23].

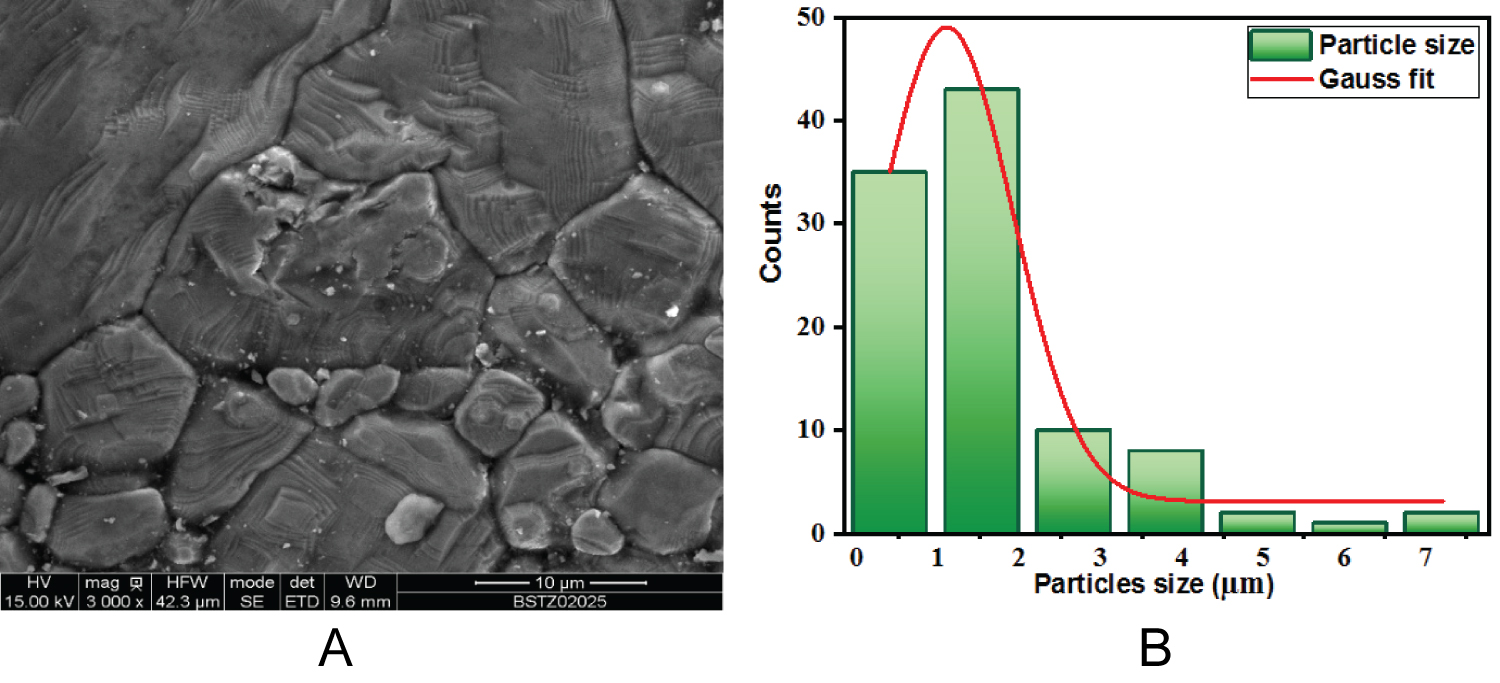
Figure 2a and Figure 2b shows a typical SEM micrograph and the size distribution histogram of the prepared BSTZ ceramic. As shown from the scanning electron microscopy image, the sample is composed of well-dense and large grains. The size distribution histogram and the length of each grain from SEM micrograph are measured with the help the ImageJ software. From the SEM micrograph, the average grain size that is obtained by taking 101 numbers of particles is approximately 1.1 μm. The morphological characteristic has been governed by the matter transport mechanism between the grains during the sintering process [24]. The estimated relative density (g/cm ³ ) value in this compound is approximately 84% of the theoretical maximum density measured by Archimedes’ method. For the studied sample, the substitution of Sr ²⁺ into Ba ²⁺ and Zr ⁴⁺ into Ti ⁴⁺ , has reduced the lattice anisotropy, and thus the prepared ceramic can be characterized by the distribution of dense grains [23].

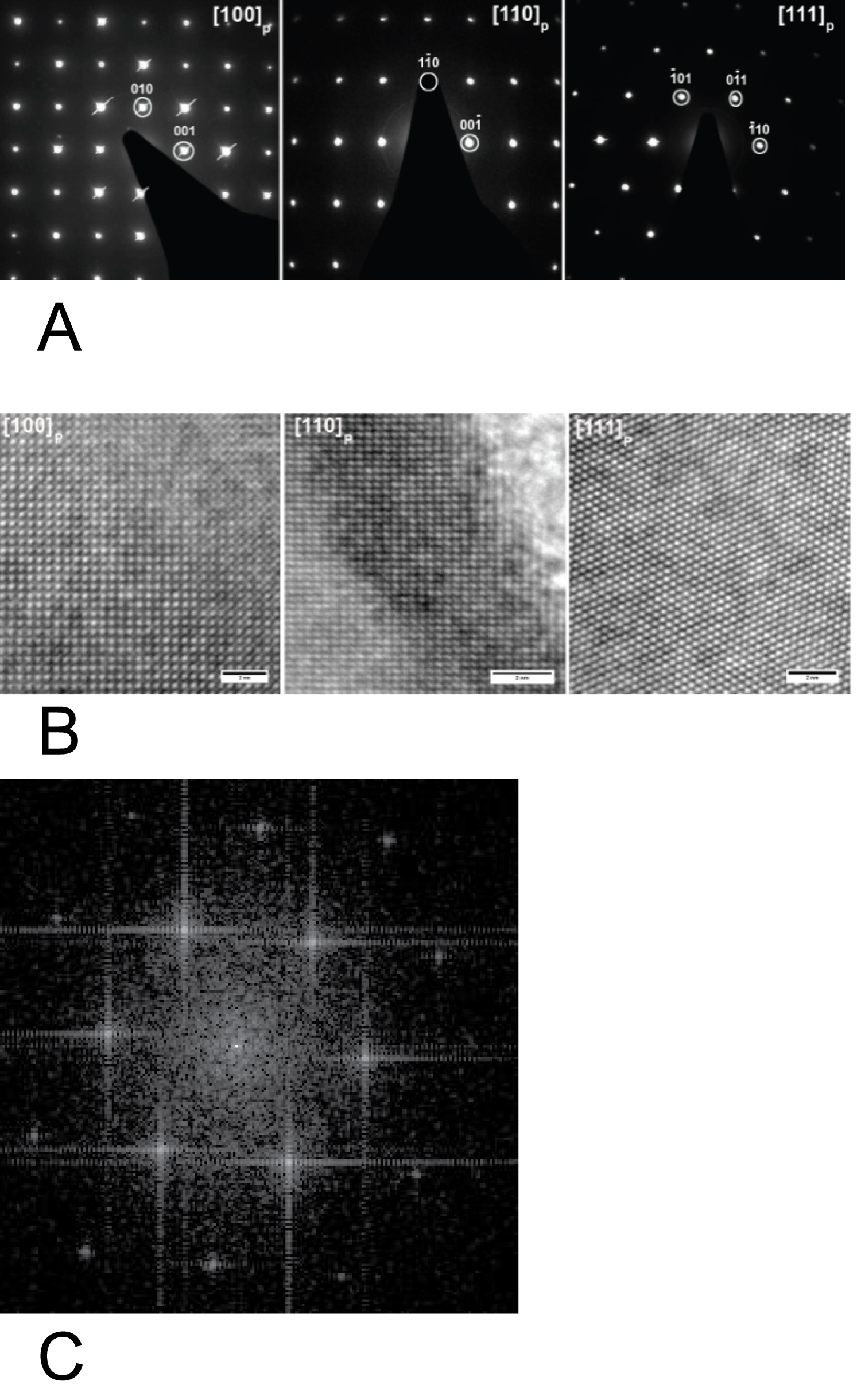
Figure 3a shows the area electron diffraction (SAED) patterns of the studied ceramic. All selected areas can be indexed using a tetragonal perovskite unit cell with the same lattice parameters that are obtained from the profile pattern adjustment of the XRD results. From the AED patterns, the absence of additional super-reflections confirms the nonexistence of local structure distortion Figure 3b shows the High-resolution TEM images in the BSTZ grains along three typical [100], [110], and [111] zone axes. The TEM study is employed to judge the space group of the prepared perovskite by identifying the super-lattice diffraction spots in a defined structure. All TEM images show clear spots corresponding to the projected atomic column without any contrast variation for [100], [110] zone axis. The presence of local dark contrast in [111] High-resolution TEM can be related to the local defect. From Figure 3c, the fast Fourier transform (FFT) calculation shows the absence of super-reflection and confirms the existence of tetragonal distortions.

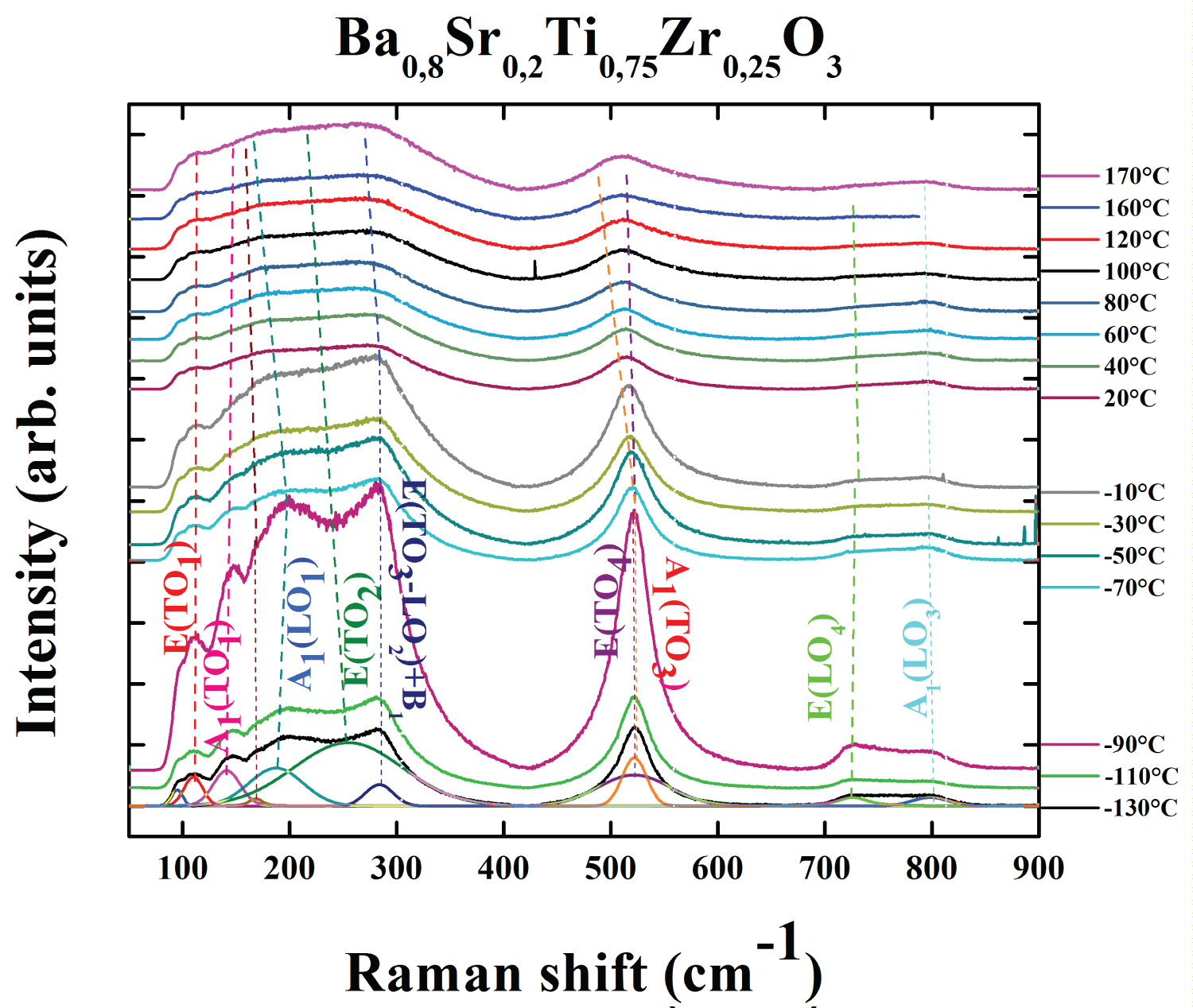
Figure 4 shows the Raman scattering spectra for BSTZ ceramic recorded up to 900 cm ^-1 and for numerous temperatures ranging from -130 °C to 170 °C. From the measured Raman intensity, the spectra are corrected using the Bose-Einstein temperature parameter to eliminate the contribution of the Bose-Einstein population factor. The reduced Raman intensities in Figure 4 are obtained by dividing the measured Raman intensity I (ν) by n (ν) +1 where n (ν), is the Bose-Einstein Factor that is given by the following relation:

$$n\left(\nu \right)=\frac{1}{e^{\left(\frac{h\nu }{k_{B}T}\right)}-1}\text{ (1)}$$

For the studied Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ ceramic, the calculated tolerance factor value t = 0.9443 confirms that the structure undergoes distortions for instance rotations of BO ₆ octahedral, and (anti)-parallel displacement of A or B cations. These distortions reduce the crystal symmetry. In addition, temperature has a great impact on crystalline symmetry. Thus, the intensity of the bands exhibits a significant downward trend with increasing temperature. As observed from Figure 4 the spectra are divided into three temperature domains, which display two-phase transition at about -70 °C and 20 °C. The broadness of all the Raman spectra arises because of disorder in the A-site and B-site induced by the substitution of Sr in the Ba-site and Zr in the Ti-site.

In the absence of disorder, the expected Raman active vibration modes for the rhombohedra phase of BSTZ is Ґ _{R3c, Raman} = 9A ₁ +9E. The A ₁ and E modes are both infrared. The A ₁ symmetry is related to lattice displacements parallel to the c-axis of the unit cell, while the doubly-degenerated E mode is associated with phonons propagating perpendicular to the c-axis [25]. The E and A ₁ modes split into longitudinal (LO) and Transverse (TO) components due to long-range electrostatic forces associated with lattice iconicity (O-Ba/Sr-O-Ti/Zr-O) [26]. In general, most of the modes are visible for the rhombohedra structure. At T= -130 °C, the deconvolution of the Raman spectrum shows the existence of multiple bands at about 254 cm ^-1 [E], 283 cm ^-1 [A ₁ ], 725 cm ^-1 [E], and 800 cm ^-1 [A ₁ ] that represent the rhombohedra phase of the material. By increasing the temperature, the degree of crystallinity of the prepared sample increases. Else, the main spectral features for T = -70 °C and at approximately 109 cm ^-1 [E], 260 cm ^-1 [E], 284 cm ^-1 [E], 521 cm ^-1 [A ₁ ], 722 cm ^-1 [A ₁ ] and 758 cm ^-1 [A ₁ ] improve the phase transition from rhombohedra to an orthorhombic structure.

At T = 20 °C, the reported results confirm the disappearance of the bands located at 187 cm ^-1 and 760 cm ^-1 and shifts of the 284 cm ^-1 band. All these changes indicate that the orthorhombic to tetragonal phase transition has occurred, which confirms the XRD results that is discussed previously. Above 20 °C, the presence of typical sharp peaks in the Raman spectra confirms also the tetragonal structure of BSTZ ceramic. The presence of 512 cm ^-1 peak and the deviation of 269 cm ^-1 , 530 cm ^-1 bands to high frequencies with increasing temperature correspond to the TO modes of A ₁ . For the studied compound, the existence of broad peaks at about 283 cm ^-1 [E] and 114 cm ^-1 [E] and the flattening of other bands from T = 120 °C in the Raman spectra characterize the phase transition from tetragonal to cubic in Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ [27]. In the case of cubic structure, the aforementioned modes suggest the presence of polar [TiO ₆ ] distorted clusters. Besides, the E stretching mode (O-Ti-O-Zr) at around 512 cm ^-1 is due to the formation of [TiO ₆ ] clusters over a short range [24]. Compared with the lead-BaTiO ₃ ceramic, the investigated Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ sample reveals low intensity modes, indicating that the non-polar [ZrO ₆ ] clusters can reduce the dipolar interaction between the polar [TiO ₆ ] clusters [28].

Dielectric Properties

In the temperature-dependent dielectric permittivity, the appearance of broad peak is among the most important characteristics of relaxor ferroelectric systems. For classical relaxor perovskites, elevated frequency dispersion can be noticeable at the low-temperature slope of the peak. At elevated temperatures, a frequency independent permittivity slope is usually observed. In addition, the maximum permittivity peak observed at T _m can shift to high temperature range against the frequency increase, following the typical Vogel-Fulcher character. Due to the existence of a permittivity anomaly and approximately other characteristics, relaxor materials can be categorized as ferroelectric systems exhibiting a diffused phase transition. Below the characteristic T _m temperature, a change from the non-ergodic relaxor phase into a non-ergodic glassy phase is reported for the well-known PbMg _1/3 Nb _2/3 O ₃ oxide. In the other hand, a transformation to a normal ferroelectric phase has been also observed in numerous solid systems like the PbMg _1/3 Nb ₂ /3O ₃ -PbTiO ₃ and PbSc _1/2 Nb _1/2 O ₃ oxides.

Above T _m , the Curie-Weiss law often explains the temperature-dependent permittivity and the paraelectric to normal ferroelectric phase changes. In dielectric relaxors, the aforementioned law is associated to the displaced-nature ferroelectric mode. In the literature, the dielectric peaks nature and other characteristics of relaxor systems are under wide investigation. In one hand, it has been suggested that the appearance of a dielectric peak can be due to the relaxation reorientation of polar areas that have limited sizes of approximately dozens of nanometers. In the other hand, the dielectric peaks are attributed to the relaxation of the polar boundary zones.

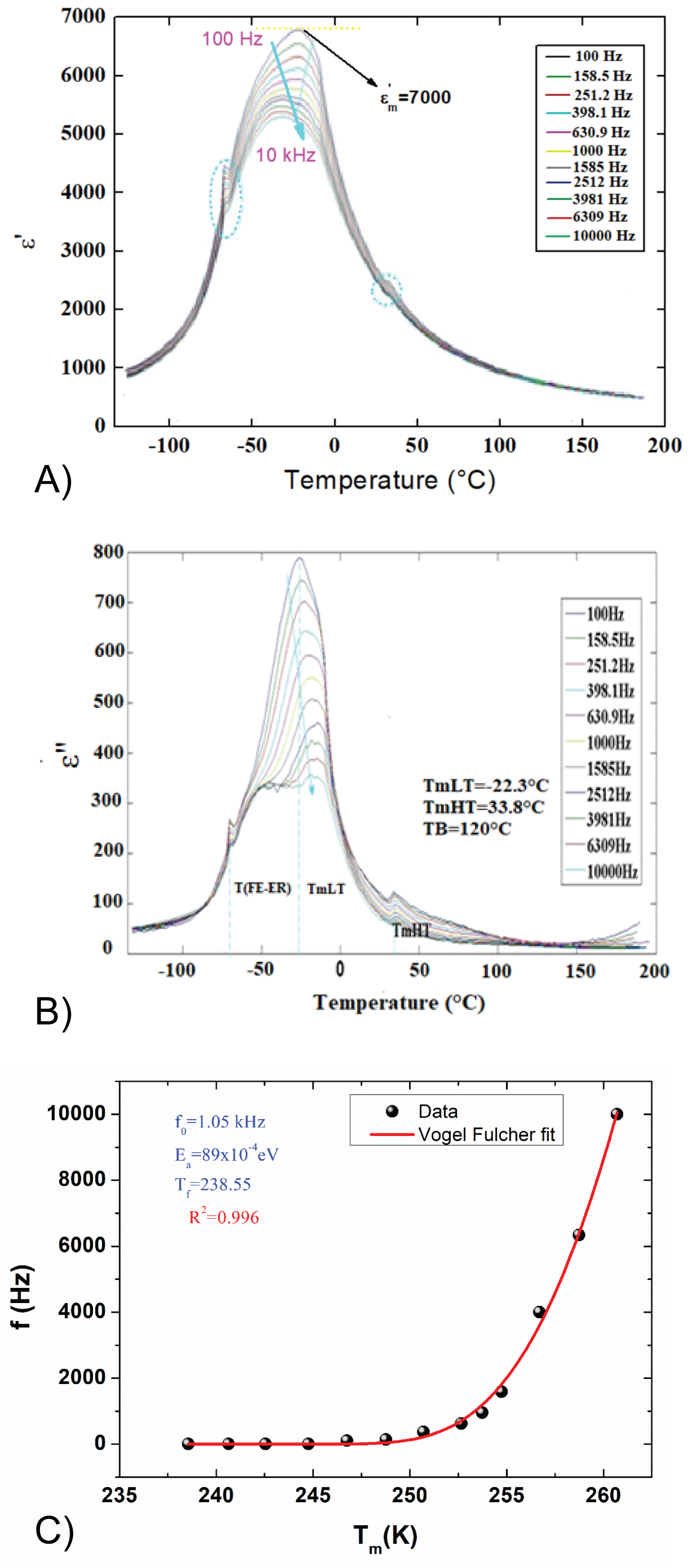
For the studied compound, the temperature dependence of the real (ε’)and imaginary (ε”) parts of permittivity, measured at different frequencies between 100 Hz and 10 kHz, is shown in Figure 5a and Figure 5b, respectively. The figures show a typical behavior, as found in a dipolar relaxor with a broad temperature, ∆T _m = 12.1 °C, depending on the maximum of the dielectric permittivity ε’ _m . Another characteristic feature of the relaxor in this sample is the considerable dispersion znear the maxima in both real and imaginary parts of the permittivity. This result leads to a dramatic slow relaxation frequency with temperature.

As compared with relaxor ferroelectric systems like Ca _0.5 Sr _0.5 Ba _0.5 Pb _0.5 Nb ₂ O ₇ [1] that reveals elevated relative permittivity ε’ = 130, the reported results in Figure 5a indicate that the studied ceramic is characterized by elevated dielectric permittivity that reach ε’ _m ≈ 7000 and very low dielectric losses of tan(δ) = 0.1. The aforementioned results establish a basis for the application of Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ in capacitor devices due to the high-performance dielectric energy storage of lead-free perovskite systems. For Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ , the dispersion vanishes at Burn’s temperature T _B = 120 °C [29]. These unusual behaviors arise as a result of frustrating interactions and random fields [20]. The frequency of the maxima ε” _m diverges at the freezing temperature T _f according to the well-known Vogel-Fulcher relation [30]

$$f\left(T\right)=f_0{\exp }^{\left(\frac{-E_a}{k_B\left(T-T_f\right)}\right)}\text{ (2)}$$

The parameter f ₀ is pre-exponential factor. T _f and k _B are the freezing temperature and the Boltzmann constant, respectively. The maxima in the temperature dependence of the imaginary part of the dielectric constant ε” are better defined [30], and therefore, the freezing temperature has been determined from them. The temperature-dependent characteristic relaxation frequency, determined from the ε” _m (T) peaks, is shown in Figure 5c, and is found to follow the Vogel-Fulcher law. The best-fit analysis of the data is obtained with f ₀ = 1.01 MHz and a freezing temperature of T _f = -34.34 °C.

In the present work, the most important result seems to be the existence of two shoulders indicating two-phase’s transitions, as reported in characterization with Raman scattering. The first is a diffuse Paraelectric (PE) to Ergodic Relaxor (ER) phase transition at T _B = 120 °C and the second is a diffuse (ER) to Ferroelectric (FE) phase transition at T _ER-FE = -70.3 °C, which implies macroscopic isotropy for the dielectric properties [31]. At high temperatures (T > T _B ), the dielectric behavior and the high temperature slope of the permittivity are similar to that of the normal ferroelectrics and follow the Curie Weiss law described by the following relation:

$$\frac{1}{{\epsilon }^{\text{'}}}=\frac{T-T_{CW}}{C}\text{ (3)}$$

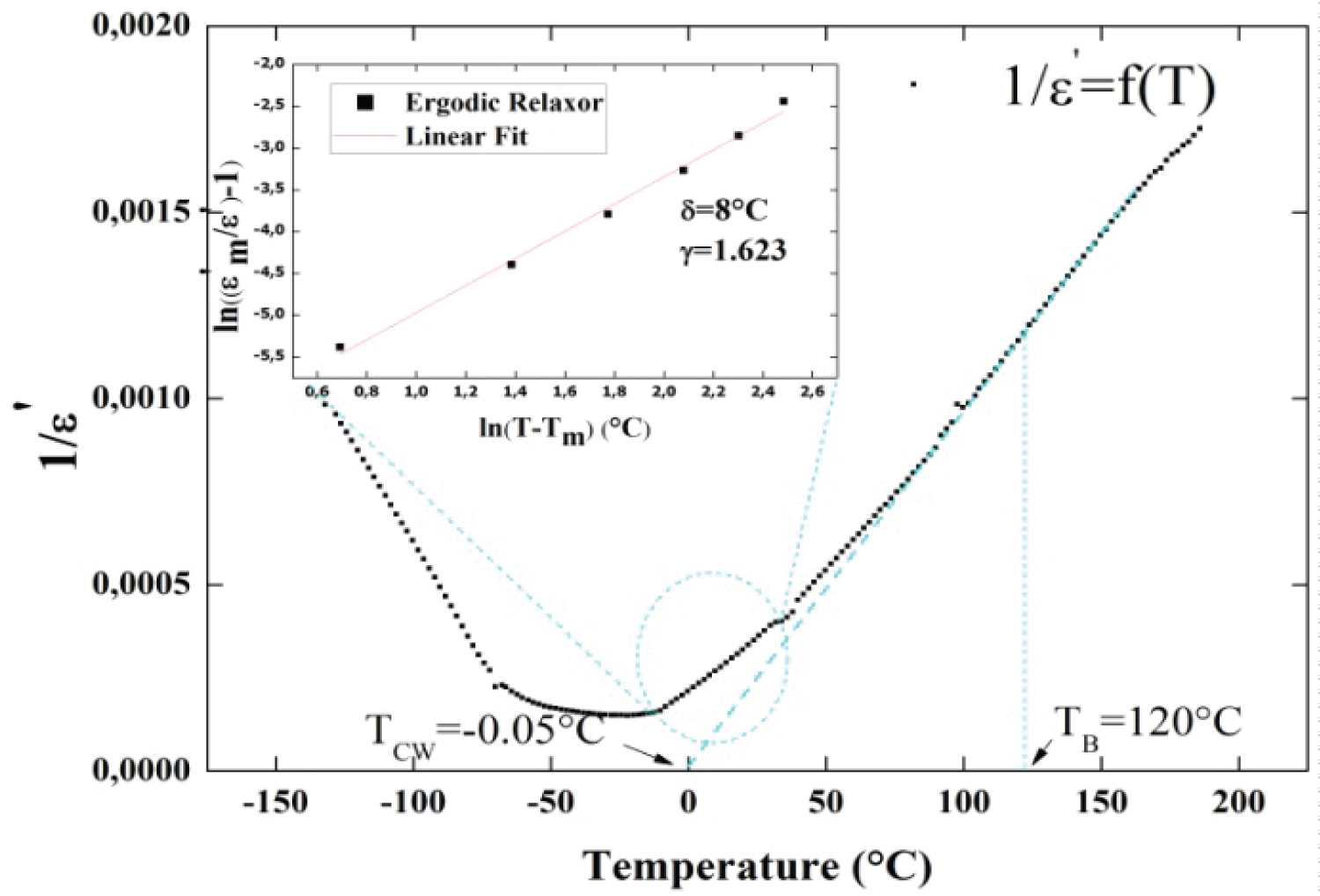
T _CW and C are the Curie-Weiss temperature and the Curie-Weiss constant, respectively. For relaxor systems, the current ferroelectric phase transitions theories do not suggest the general Curie Weiss law formula to analyze the dielectric character of ferroelectrics. Hence, it is satisfying to find it out from the experimental data to offer the basis for additional theoretical studies. Accordingly, and from the temperature dependence of the inverse of the dielectric constant (Figure 6), the deduced T _CW and C parameters are T _CW = -0.05 °C and C = 1.0788 × 10 ⁵ °C.

For instance, in the temperature range T _ER-FE <T<T _B , two anomalies have been observed: The first is the maxima at low-temperature T _mLT = -22.3 °C and the second occurred at high-temperature T _mHT = 33.8 °C. It is worth noting that these two maxima have been observed in PMN annealed at T = 400 °C for 28 hours with slow cooling to room temperature for 12h [32]. Note also that these two anomalies have different positions and intensities, which depend on electric dipoles and other defective (random field source) features as well as single dipole dynamic parameters [33]. The first maximum representing the dielectric constant and decreases with increasing frequency. This behavior suggests a decrease in polarization in the studied ceramic. At low frequencies, various types of polarization (electronic, ionic, dipolar, and interfacial) can be observed in dielectric systems. While, by increasing the frequency, ionic, dipolar and interfacial polarization disappeared little by little and only electronic polarization resisted [34]. Such behavior is well known to be characteristic of relaxation processes. The dielectric permittivity magnitude increases with electric dipole concentration and decreases with the point charges or dilatational centers concentration increase [33]. Thereby, below T _mHT , this complex polarization induced in BSTZ is the origin of the dielectric relaxation into ER phase in a particular frequency interval [35]. It could be associated with the formation of PNRs structure, which evolves with temperature and interacts with particular mechanisms such as the phonon polarization mechanism. The aforementioned phenomena contribution strongly and govern the intrinsic dielectric response of the materials [31,36].

Furthermore, the reported results show a considerable broadening of the peak in the maximum of the permittivity. W. Ge, et al. [37] have found the same feature in PZT, and they have explained this behavior by the correlation of the short-range of Pb atom displacements because of local repulsive interactions, which could affect the distribution of the B site (Zr/Ti) elements. In the frequency range between 100 Hz and 10 kHz, the relative permittivity can be written as:

$$n\left(\nu \right)=1+{\chi }_R+{\chi }_U\text{ (4)}$$

The parameters χ _R and χ _U are the susceptibilities describing the “conventional relaxation” (CR) and the “universal relaxation” (UR) respectively. By increasing the frequency, the position of the broad maxima ε’ _m has shifted to the low temperature region. Such result is different from the dispersion in the CR. Thus, the specific dipole reorientation mode of PNRs and fluctuations of PNRs boundaries contribute to the dielectric response below T _B [38], which might create inhomogeneity for the hopping carriers, giving rise to unusual UR behavior.

Bokav, et al. [39] have parameterized the diffuseness ɣ of the permittivity peak and the deviation parameter δ from the Curie Weiss low in relaxor by fitting the maximum temperature T _mLT slope of the diffuse permittivity peak using an empirical Lorenz-type relation:

$$\frac{{\epsilon }_m^{\text{'}}}{{\epsilon }^{\text{'}}}=1+\frac{{\left(T-T_m\right)}^{\gamma }}{2{\delta }^2}\text{ (5)}$$

If ɣ = 1a normal phase transition could be described by Curie-Weiss law, while the dependence of 1/ε’ on (T-T _m ) is reduced to a quadratic variation that describes a complete diffuse phase transition for ɣ = 2. Figure 6 shows the Curie Weiss fit of the real part of the permittivity data of Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ ceramic at 100 Hz. The inset shows the fitting experimental data using equation (5). The linear fit gives the degree of diffuseness ɣ of the permittivity peak and the deviation parameter δ from the Curie Weiss low.

In the inset of Figure 6, a plot of  as a function of  confirms the occurrence of relaxor behavior in BSTZ. From the linear fit results, in the temperature range between -20 °C and -10 °C, the deduced values of the diffuseness degree and deviation parameter are ɣ = 1.623 and δ = 8 °C. The ɣ value suggests that the material has both structural order-disorder and diffuse phase transition behaviors.

Conclusions

In the present work, Polycrystalline relaxor Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ material is prepared using the conventional solid-state reaction route. The structural studies indicate that the studied compound reveals a single phase with P4mm space group. Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ solid solution behaves as a lead-free relaxor system. The present study has revealed several relaxor features of BSTZ with underlying the structural disorder, which is the main responsibility on the polar nano-regions PNRs appearance. Thus, the imaginary part of the dielectric permittivity has been analyzed using the temperature-frequency plots and shows that the maximum spectra relaxation obeys the Vogel-Fulcher relaxation. Besides, the Curie Weiss fit of the real part of the permittivity (using an empirical Lorenz-type relation) reveals that the material has both structural order-disorder and diffuse phase transition. Although, the presence of PNRs and their evolution with temperature and frequency make distinctive features of relaxor behavior appear such as the two kinds of relaxation: “conventional relaxation” (CR) and “universal relaxation” (UR). In this paper, it is also demonstrated that PNRs associated with relaxor behavior provide an intrinsic structural inhomogeneity to the crystal lattice, which causes the birth of new anomalies in the permittivity as function as temperature. The elevated relative permittivity and the lower dielectric losses establish a basis for the application of Ba _0.8 Sr _0.2 Ti _0.75 Zr _0.25 O ₃ in capacitor devices due to the high-performance dielectric energy storage.

Data Availability Statement

No Data associated in the manuscript.

References

1. Hu Z, H Zhang, John Reece M, et al. (2023) Relaxor ferroelectric behaviour observed in (Ca ₅ Sr _0.5 Ba _0.5 Pb _0.5 ) Nb ₂ O ₇ perovskite layered structure ceramics, J Eur Ceram 43: 362-369.
2. Long Ch, Zhou W, Liu L, et al. (2023) Achieving excellent energy storage performances and eminent charging-discharging capability in donor (1-x) BT-x (BZN-Nb) relaxor ferroelectric ceramics J Chem Eng 459: 141490.
3. Reavley M JH, Guo H, Yuan J, et al. (2022) Ultrafast high-temperature sintering of barium titanate ceramics with colossal dielectric constants. J Eur Ceram Soc 42: 4934-4943.
4. Anjum TA, Naveed-Ul-Haq M, Hussain S, et al. (2020) Rafique, Analyses of structure, electronic and multiferroic properties of Bi _1-x Nd _x FeO ₃ (x = 0, 0.05, 0.10, 0.15, 0.20, 0.25) system. J Alloys Compd 820: 1-10.
5. Zuo J, Yang H, Chen J, et al. (2023) Highly-reliable dielectric capacitors with excellent comprehensive energy-storage properties using Bi ₅ Na _0.5 TiO ₃ -based relaxor ferroelectric ceramics. J Eur Ceram Soc 43: 2452-2459.
6. Martin LW, Ramesh R (2012) Multiferroic and magnitoelectric heterostructures. Acta Mater 60: 2449-2470.
7. Chen L, Yu H, Deng Sh, et al. (2023) High energy storage performance in BaTiO ₃ -based lead-free relaxors via multi-dimensional collaborative design. J Eur Ceram 43: 2417-2425.
8. Uddin S, Faisal S, Zaman A, et al. (2023) Investigation of impact of Zr-doping on the structural and microwave dielectric properties of CaTiO ₃ Opt Mater 135: 113358.
9. Chlup Z, Drdlík D, Hadraba H, et al. (2023) Temperature effect on elastic and fracture behaviour of lead-free piezoceramic BaTiO3. J Eur Ceram Soc 43: 1509-1522.
10. Tihtih M, Eldin J, MIbrahim F, et al. (2023) Enhancedoptical and thermal conductivity properties of barium titanate ceramic via strontium doping for thermo-optical applications. Opt Quantum Electron 55: 1-20.
11. Sun M, Wang X, Li P, et al. (2023) Realizing ultrahigh breakdown strength and ultrafast discharge speed in novel barium titanate-based ceramics through multicomponent compounding strategy. J Eur Ceram Soc 43: 974-985.
12. Li Y, Tang M-Y, Zhang ZG, et al. (2023) BaTiO3-based ceramics with high-energy storage density. Rare Metals 87: 1-13.
13. Belhajji M, Nfissi A, Sayouri S, et al. (2023) Investigation of the structural, microstructural and dielectric properties of rare earth La- and Ho-doped PbTiO3 for piezoelectric applications. J Mater Sci: Mater Electron 34: 1-15.
14. Tihtih M, M Ibrahim J EF, Basyooni MA, et al. (2023) Role of A-site (Sr), B-site (Y), and A, B sites (Sr, Y) substitution in lead-free BaTiO3 ceramiccompounds: Structural, optical, microstructure, mechanical and thermal conductivity properties. Ceram Inter 49: 1947-1959.
15. Shang M, Ren P, Wan Y, et al. (2023) Tailoring Curie temperature and dielectric properties by changing the doping sites of Y ions in (Ba, Ca)(Zr, Ti)O3 ceramics. J Eur Ceram Soc 43: 2488-2497.
16. Ben Abdessalem M, Aydi S, Aydi A, et al. (2017) Polymorphic phase transition and morphotropic phase boundary in Ba1-xCaxTi1-yZryO3 ceramics. Appl Phys A 583: 2-10.
17. Abdessalem M, Kriaa I, Aydi A, et al. (2018) Large electro-caloriceffect in lead-free Ba1-xCaxTi1- yZryO3 ceramics under strong electricfield at room temperature Ceram. Inter 44: 13595-13601.
18. Ben Abdessalem M, Aydi A, Abdelmoula N, et al. (2019) Raman scattering, structural, electrical studies and conduction mechanism of Ba0.9Ca0.1Ti0.95Zr0.05O3 ceramic, J Alloys Comp 774: 685-693.
19. Zheng H, Zhao L, Ma Z, et al. (2023) Synergic and competitive effect of A-site substitution on structure and electricproperty in BaTiO3-based ceramics. J Alloys Comp 937: 16835.
20. Wang D, Bokov AA, Ye Z-G, et al. (2016) Subterahertz dielectric relaxation in lead-free Ba (Zr, Ti) O3 relaxor ferroelectrics. Nat Commun 7: 1-7.
21. Xie L, Li YL, Yu R, et al. (2012) Static and dynamic polar nanoregions in relaxor ferroelectric Ba(Ti1−xSnx)O3 system at high temperature. Phys Rev 85: 1-5.
22. Bain AK, Chand P (2013) Optical properties of ferroelectrics and measurement procedures. Adv Ferroelectrics, Books.
23. Kleemann W, Miga S, Dec J, et al. (2013) Crossover from ferroelectric to relaxor and cluster glass in BaTi1−xZrxO3 (x = 0.25-0.35) studied by non-linear permittivity. Appl Phys Lett 102: 232907.
24. Lee SH, Lee SG, Lee YH, et al. (2012) Electrical properties of lead-free 0.98(Na0.5K0.5) NbO3-0.02Ba (Zr0.52Ti0.48) O3 piezoelectric ceramics by optimizing sintering temperature. Nanoscale Res Lett 7: 1-5.
25. Badapanda T, Rout SK, Cavalcante LS, et al. (2009) Optical and dielectric relaxor behaviour of Ba(Zr0.25Ti0.75)O3 ceramic explained by means of distorted clusters. J Phys D Appl Phys 42: 175414.
26. Zhu J, Zhang J, Jiang K, et al. (2016) Coexistence of ferroelectric phases and phonon dynamics in relaxor ferroelectric Na0.5Bi0.5TiO3 based single crystals. J Am Ceram Soc 99: 2408-2414.
27. Di Domfnrro M, Wemple SH Jr, Porto SPS, et al. (1968) Raman spectrum of single-domain BaTiO3. Phys Rev 174: 522-530.
28. Begg BD, Finnie KS, Vance ER (1996) Raman Study of the relationship between room-temperature tetragonality and the curie point of barium titanate. J Am Ceram Soc 79: 2666-2672.
29. Karan NK, Katiyar RS, Maiti T, et al. (2009) Raman spectral studies of Zr4+-rich BaZrxTi1−xO3(0.5 ≤ x ≤ 1.00) phase diagram. J Raman Spectrosc 40: 370-375.
30. Brajesh K, Tanwar K, Abebe M, et al. (2015) Relaxor ferroelectricity and electric-?eld-driven structural transformation in the giant lead-free piezoelectric (Ba, Ca)(Ti, Zr)O3. Phys Rev B92: 224112.
31. Bovok AA, GYE Z (2006) Recent progress in relaxor ferroelectrics with perovskite structure. Front Ferroelectr 41: 31-52.
32. Filipic C, Kutnjak Z, Pirc R, et al. (2016) BaZr0.5Ti0.5O3: Lead-free relaxor ferroelectric or dipolar glass. Phys Rev B 93: 224105.
33. Laguta V, Glinchuk M, Kndakava I, et al. (2004) Anomalies of dielectric response in mixed ferro-glass phase of potassium tantalate doped by Lithium. Ferroelectrics 298: 171-182.
34. Glinchuk MD, Stephanovich VA (1999) Dynamic properties of relaxor ferroelectrics. J Appl Phys 85: 1722- 1726.
35. Sen S, Choudhay RNB (2004) Effect of doping Ca ions on structural and electrical properties of Ba (Zr0.05Ti0.95) O3 electro-ceramics. J Mater Sci 15: 671-675.
36. Jonscher AK (1999) Dielectric relaxation in solids. J Phys D: Appl Phys 32: R57-R70.
37. Bovtun V, Petzelt J, Porokhonskyy V, et al. (2001) Structure of the dielectric spectrum of relaxor ferroelectrics. J Euro Ceram Soc 21: 1307-1311.
38. Ge W, Devreugd CP, Phelan D, et al. (2013) Lead-free and lead-based ABO3 perovskite relaxors with mixed-valence A-site and B-site disorder: Comparative neutron scattering structural study of (Na1/2Bi1/2)TiO3 and Pb(Mg1/3Nb2/3)O3. Phys Rev B88: 174115.
39. Bokov AA, Ye ZG (2002) Universal relaxor polarization in Pb (Mg1/3Nb2/3) O3 and relatedmaterials. Phys Rev B 66: 064103.