Global Dynamics of SARS-Cov-2 Virus-Cell Model Including Inflammatory Responses to Lung Cells
Abstract
SARS-CoV-2 is the pathogen of COVID-19, which has caused a pandemic worldwide at the beginning of 2020. The clinical symptoms of SARS-CoV-2 infection are not identical, and the infected person can suffer from common cold to more severe diseases, such as pneumonia, which is an important cause of COVID-19 deaths. Virus dynamical behaviors of SARS-CoV-2 in vivo of infected persons determine their different clinical symptoms. In this paper, a new virus-cell model is proposed to study the dynamical behavior of SARS-CoV-2 including inflammatory responses, and then the global dynamics of this model are studied. By persistence theory and constructing Lyapunov functions, it shows that if Rc < R0 < 1, the infection-free equilibrium of the model is globally asymptotically stable, which implies COVID-19 can heal itself in vivo. If Rc < 1 < R0, the infected equilibrium without inflammatory is globally asymptotically stable, which implies SARS-CoV-2 would persistently exist in vivo without inflammatory response. If 1 < Rc < R0, the infected equilibrium with inflammatory is globally asymptotically stable, which implies SARSCoV-2 would persistently exist in vivo with inflammatory response. By the simulations, it shows that the activation of inflammatory cells would change the chest radiograph score of lung cells.
Keywords
SARS-CoV-2, COVID-19, Inflammatory response, Lyapunov function, Persistence theory
Introduction
The pathogen, Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), has infected more than 11,000,000 people worldwide and the coronavirus disease it causes, Corona Virus Disease 2019 (COVID-19), has caused more than 500,000 deaths as of June, 2020 [1]. For this pandemic, many 5 mathematical models have been proposed to study the transmission of COVID-19, especially for the estimation of its basic reproduction number R0 [2-4]. However, the virus-cell model is rarely mentioned about SARS-Cov-2, which is important in the study of virus dynamical behaviors in vivo of infected persons. And they determine the different clinical symptoms of SARS-CoV-2 infection from common cold to more severe diseases, such as pneumonia [5].
Nowak-Bangham's model was first studied in [6] to describe the virus-cell dynamics of Human Immunodeficiency Virus (HIV) in vivo. Its global stability was studied in [7,8]. In [9], the authors studied the global stability of a virus dynamics model with Beddington-DeAngelis term and immune response. For HIV, the virus-cell model has been considered to study the virus dynamics during infection-immunity processes. However, for SARS-Cov-2, the inflammation responses are more important, which would lead to pneumonia from common cold. The inflammation response is the body's defensive response to virus infection. When the body is infected, an inflammatory would respond to get rid of itself and restore health. Usually, the inflammation response is beneficial, but sometimes it can be harmful to attack the body's healthy tissues, such as lung cells. Uncontrolled inflammation due to infection can culminate in organ failure and death [10]. In view of this fact, we propose a new virus-cell model with inflammation responses, which reflects the inflammation process of SARxS-Cov-2. In the next section, we give the model description, and then we analyze the global stability of the model.
Formulation of the Model
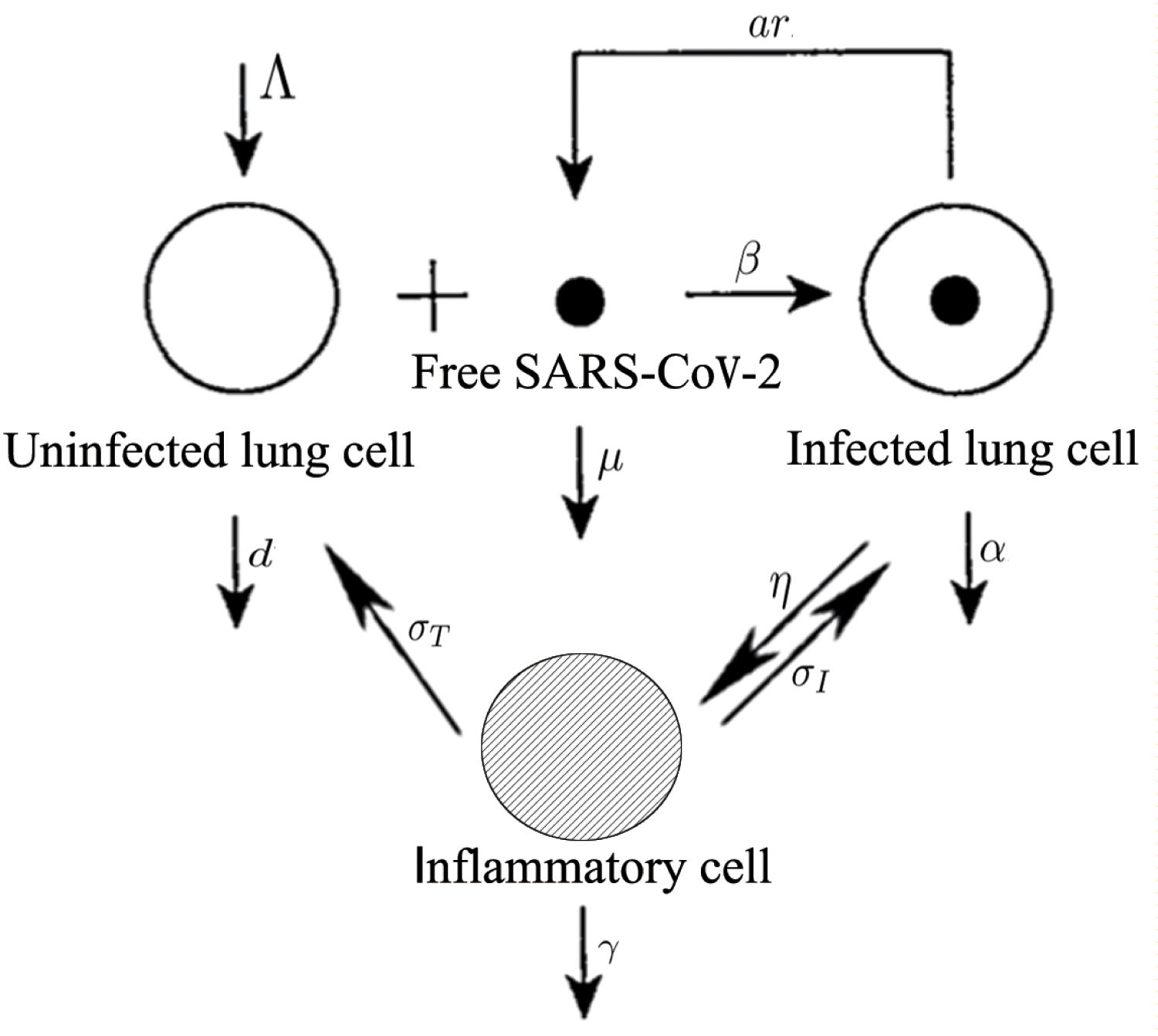
In our model, T(t) denotes the density of uninfected lung cells, I(t) denotes that of infected lung cells, C(t) denotes that of inflammatory cells and V(t) denotes that of SARS-Cov-2. The healthy lung cells are assumed to reproduce with a constant rate Λ. The average lifetime of T(t), I(t), C(t) and V(t) are 1/d, 1/α, 1/γ and 1/µ, respectively. Free SARS-CoV-2 is produced from infected lung cells at the rate ar and infects the healthy lung cells at the rate β. Inflammatory cells are activated by the infected cells at the rate η. The advantage of inflammatory cells is to kill infected lung cells at the rate σI, but the disadvantage of them is to kill the healthy lung cells at the rate of σT. All the parameters are assumed positive.
According to Figure 1, the virus-cell dynamics model of SARS-CoV-2 is established as follows:
The system (1) has an infection-free equilibrium E0 = (T0, 0, 0, 0) = ( 0, 0, 0) corresponding to the maximal level of healthy lung cells. And if the system (1) has an infected equilibrium without inflammatory By existence condition of positive equilibrium, we can get the basic reproductive number for system (1):
If Rc > 1, there also exists an infected equilibrium with inflammatory E* = (T*, I*, C*, V*),
where C* is the unique positive root of
Then we can obtain
Let ω(φ) is the ω-limit set of φ. φ is a continuous semiflow on X1, X1 is a subset in metric space with metric d. φ : [0, ∞) × X1 → X1 with φt o φs = φt+s, t, s ≥ 0; φ0(x) = x, x ∊ X1. Let the solution of system (1) be u(t) = u(t)(φ) := (S(t), I(t),C(t),R(t)). Thus, we can discuss the dynamics behavior of system (1) in the closed set And it is easy to see that D is positively invariant of system (1).
We define
D2 and are forward invariant.
Let
Ω* consists of equilibria E0, E1. These equilibria cannot be chained to each other in D1. By analyzing the flow in neighborhood of each equilibrium, it is easy to see that Ω* 40 is isolated in D and D1 is a uniform strong repeller for [11,12]. If u(t) stays close to E0, we have three cases: if I (0) = V (0) = 0, then I (t) = V (t) = 0; if I (0) > 0 or V (0) > 0, C (0) = 0 then I (t) > 0, V (t) > 0 and C (t) = 0; if I (0) > 0 or V (0) > 0, C (0) > 0 then I (t) > 0, V (t) > 0 and C (t) > 0. Therefore, E0 is isolated in D. Similarly, we can prove that E1 is isolated in D.
Analysis of Stability
Theorem 1: If Rc < R0 < 1, then E0 is locally asymptotically stable; if Rc < 1 < R0, then E1 is locally asymptotically stable. If 1 < Rc < R0, then E0 and E1 is unstable, and E* is locally asymptotically stable.
Proof: After calculation, it is shown that the Jacobian matrix of the vector field corresponding to system (1) is
The characteristic equation associated with J at E0 is given by
If Rc < R0 < 1, then all roots of equation (2) have negative real parts. Therefore, E0 is locally asymptotically stable.
At E1, the associated characteristic equation is
where
If Rc < 1 < R0, then After calculation, it is shown that A2 > 0, A0 > 0, A1 > 0 and A1A2 - A0 > 0. Thus, the Routh-hurwitz criterion implies that all roots of equation (3) have negative real parts and then E1 is locally asymptotically stable.
If 1 < Rc < R0, at least one of the roots of equations (2) or (3) has positive real part according to the calculation above, then E0 and E1 are unstable.
At E*, the associated characteristic equation is
where
After calculation, it is shown that B3 > 0, B2 > 0, B1 > 0, B0 > 0, B3B2 - B1 > 0 and Thus, the Routh-hurwitz criterion implies that all roots of equation (4) have negative real parts and then E* is locally asymptotically stable.
Theorem 2: If Rc < R0 < 1, then E0 is globally asymptotically stable in D; if Rc < 1 < R0, then E1 is locally asymptotically stable in D; if 1 < Rc < R0, then E* is globally asymptotically stable in
Proof: According to Lyapunov function
L1 is continuous on the set D. The derivative of L1 along the solution of model (1) is
It is obvious that R0 < 1 ensures for all T, I, C, V > 0.
Let u(t) = (S(t), I(t), C(t), R(t)) be the solution of system (1) with any Φ ∊ ω(φ) ⊂ D. Then the invariance of ω(φ) implies that u(t) ∊ ω(φ) for t ∊ R. Since u(t) is bounded and differentiable, if R0 < 1, Therefore, we can obtain ω(φ) = E0 and E0 is globally attractive in D. From Theorem 1, we know that E0 is locally asymptotically stable, then we get if R0 < 1, E0 is globally asymptotically stable in D.
For E1, Rc < 1 < R0 ensures the existence of it. Define Lyapunov function
L2 is continuous on the set D. The derivative of L2 along the solution of model (1) is
Let v(t) = (S(t), I(t), C(t), R(t)) be the solution of system (1) with any Φ ∊ ω(φ) ⊂ D. Since ensures then the invariance of ω(φ) implies
Therefore, we can obtain ω(φ) = E1 and E1 is globally attractive in D. From Theorem 1, we know that E1 is locally asymptotically stable, then we get if Rc < 1 < R0, E1 is globally asymptotically stable in D.
Next, we consider the stability of infected equilibrium with inflammation E* by persistence theory. Since E0, E1 are isolated in D. Using Proposition 4.3 in [11], we can prove that D1 is a uniform weak repeller for and using Theorem 4.5 in [11], we can prove that D1 is a uniform strong repeller for
Then we get that there exists an such that
with T(0) > 0, I(0) > 0, C(0) > 0 and V (0) > 0 in Therefore, if Rc < R0 < 1, E* is the unique internal equilibrium of system (1). Since system (1) is persistent in E* is locally asymptotically stable by Theorem 1, then Therefore, if Rc < R0 < 1, then E* is globally asymptotically stable in
Simulations
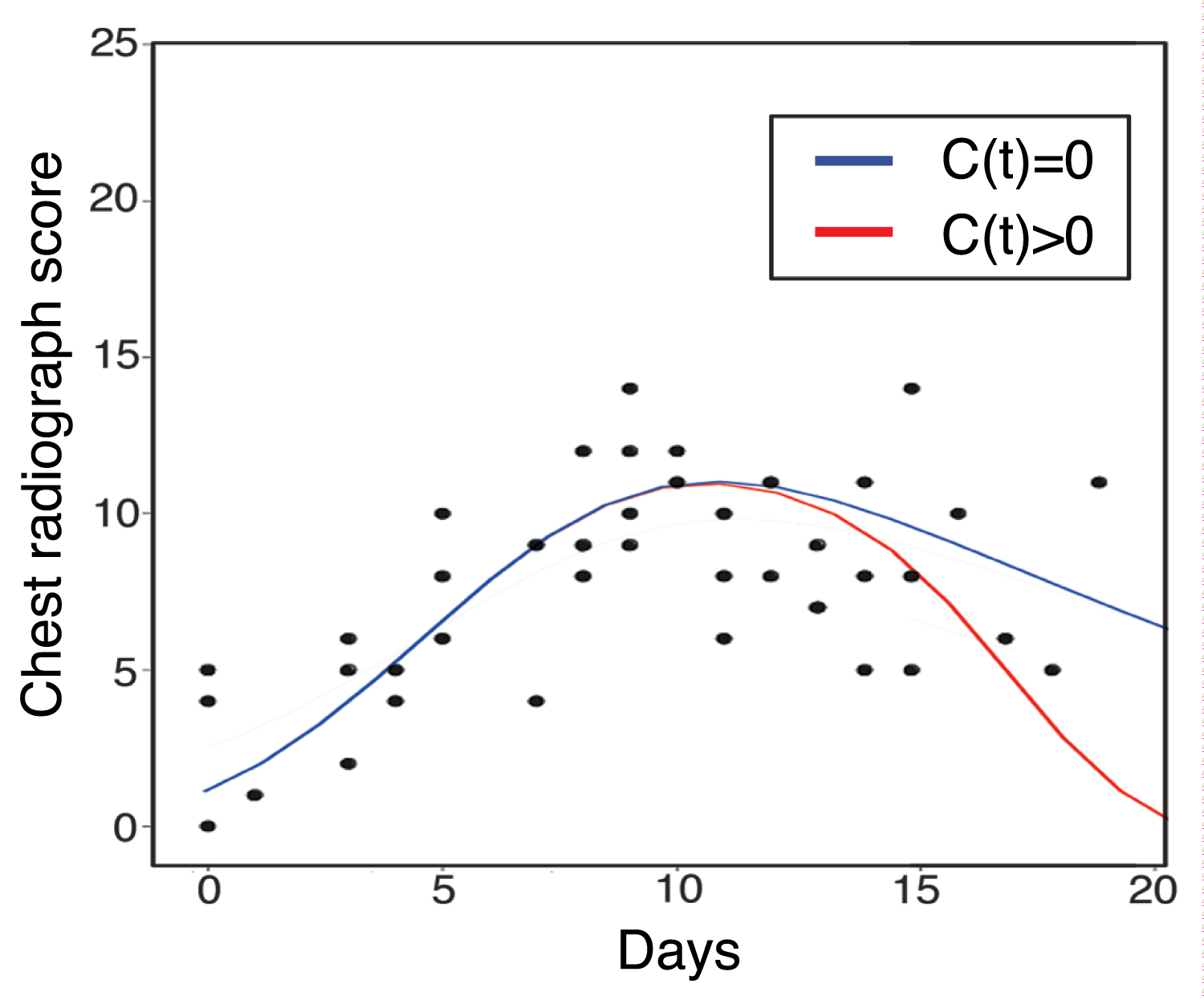
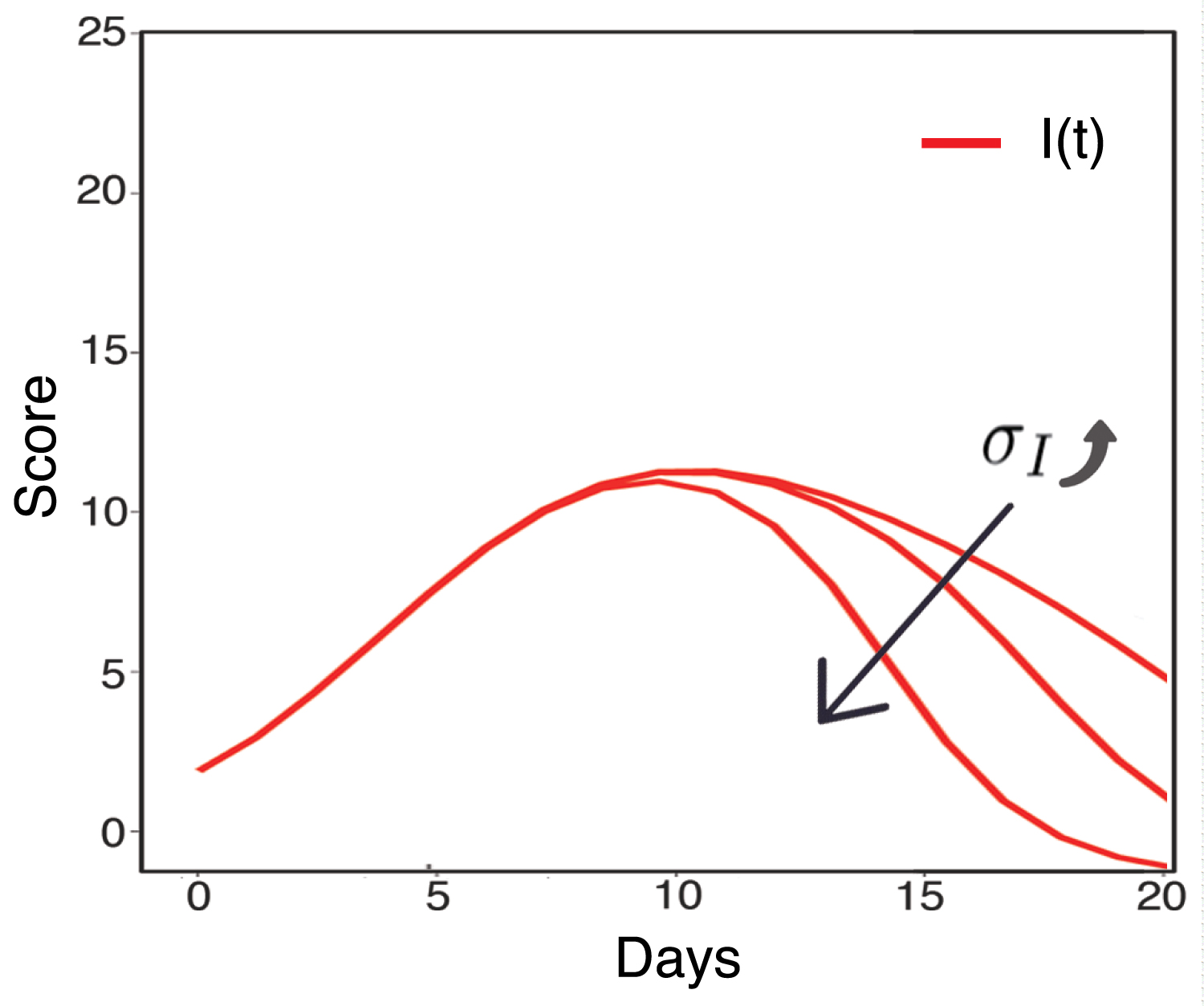
[13] has studied the virus-cell model of SARS-CoV-2 by the chest radiograph score data from serve patients (with high chest radiograph scores) [13,14]. Therefore, in this paper, we continue to consider the chest radiograph score as a way to reflect the infected lung cells by SARS-Cov-2, then we add the effect of inflammatory response by C(t) > 0. Figure 2 shows the fitted result of the model. The activation of inflammatory cells decrease the chest radiograph score more rapidly as the red line. It is the healthy response that the inflammatory cells becomes activated, clears the pathogen, and then begins a repair process and abates. The value of parameters is summarized in Table 1. Some of them were collected from [13], and others are estimated by MATLAB, using genetic algorithm. Figure 3 shows the effect of σI on the decrease of infected lung cells score, which is also proving of the advantage of inflammatory cells.
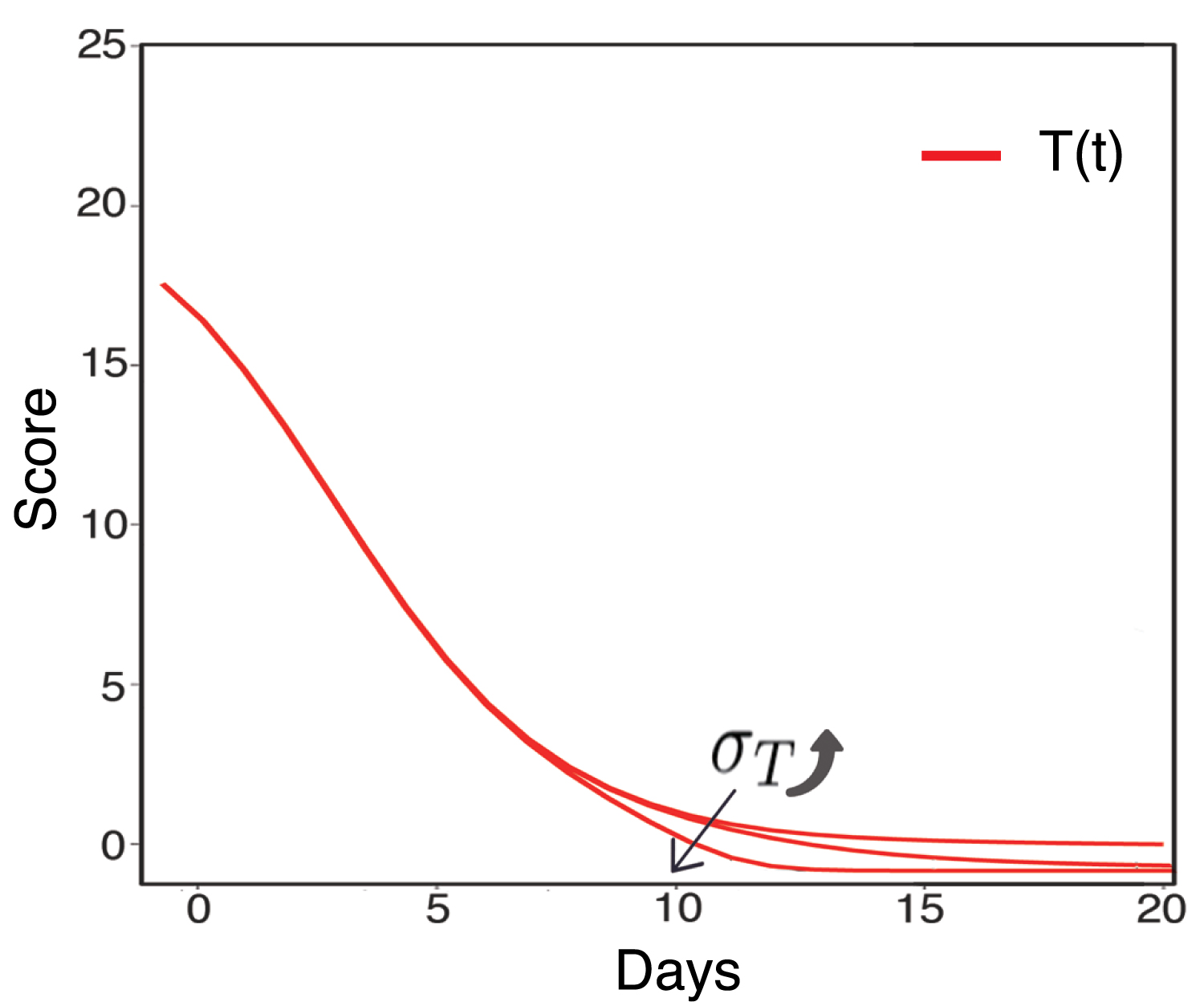
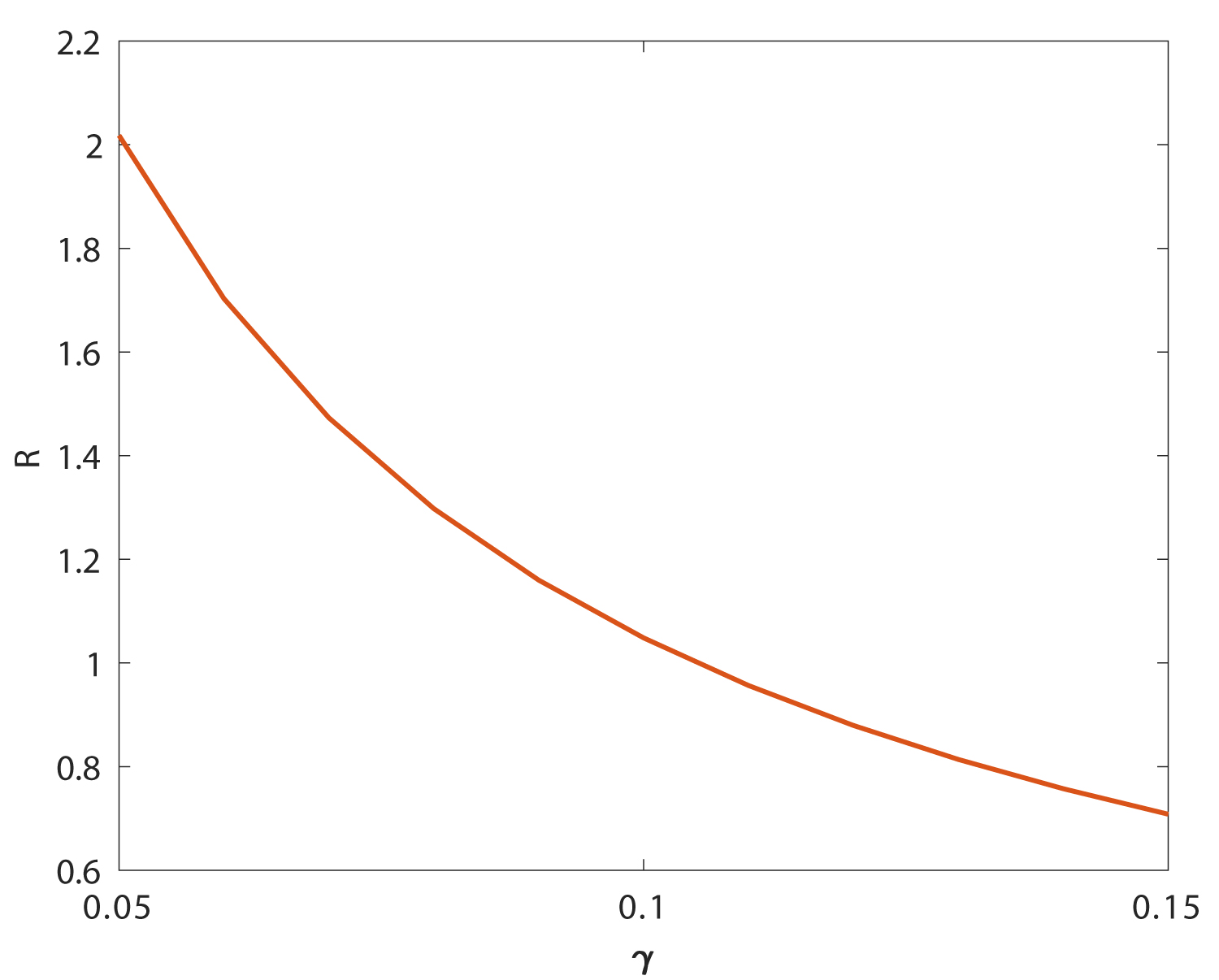
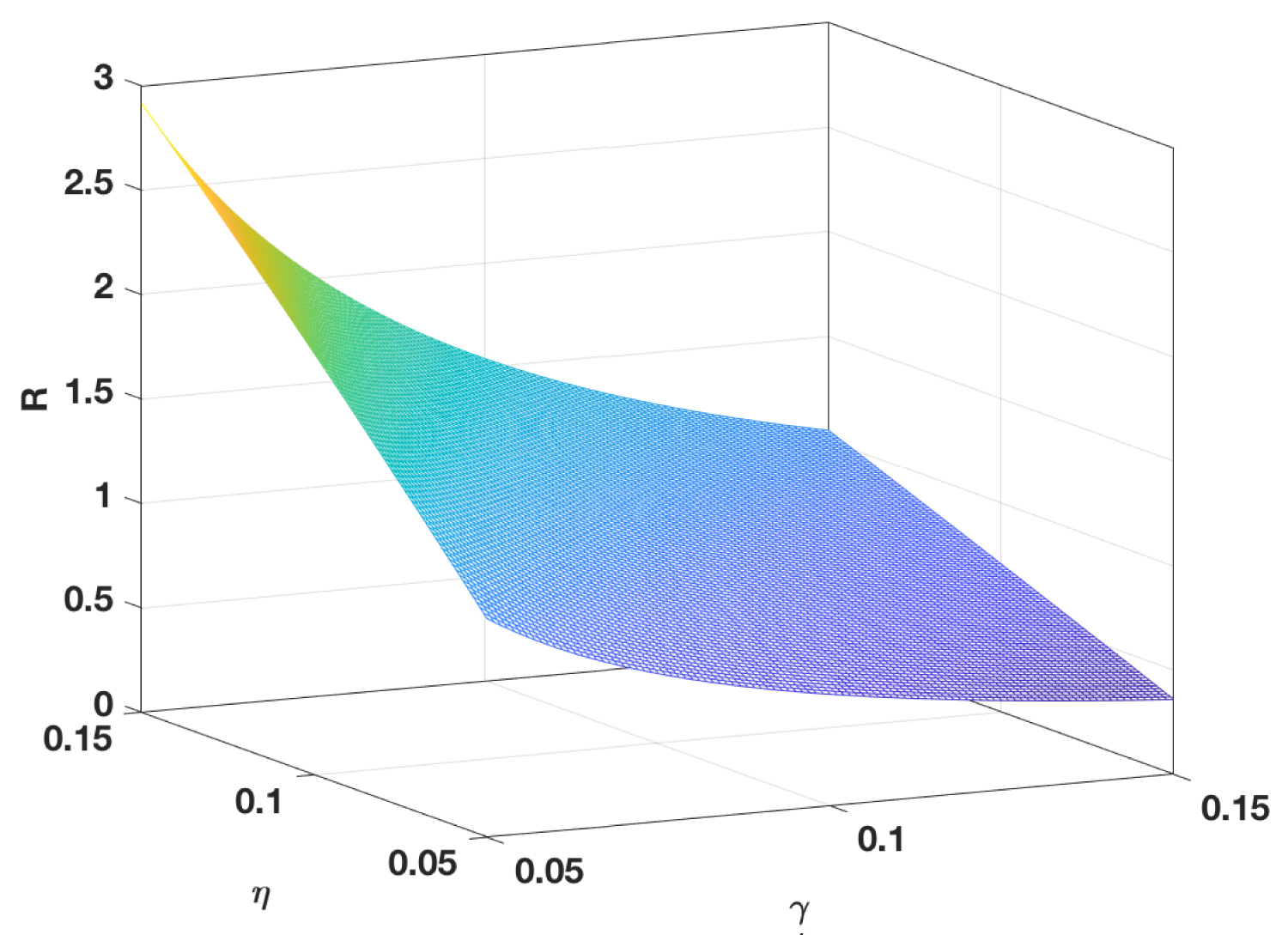
However, since the inflammatory response is non-specific and is the first line of defense of the body against viral infections, uncontrolled inflammatory response would kill more healthy infected lung cells, as shown in Figure 4. It would lead to the lung failure or even to death, which is the main cause of COVID-19 death. It is also worth noting that the activation of inflammatory cells never change the value of Rc by σI and σT. While, the value of average lifetime of inflammatory cells would change the value of Rc, as is shown in Figure 5, which implies the effect of inflammatory response on the decrease of virus infection rate in vivo. Figure 6 shows the sensitivity analysis of γ and η on Rc.
Discussion
Inflammation response is one of the reasons for fatal pneumonia caused by SARS-CoV-2. However, few studies on the mechanism of the inflammatory response during the SARS-CoV-2 infection processes in vivo. In this paper, a new virus-cell mathematical model is constructed to study the dynamical behavior of SARS-CoV-2 including inflammatory responses. Moreover, the rationality of this method is obtained through the simulations of the chest radiograph score.
Based on the stability conditions of model (1), we construct the basic reproductive number of the model, Rc. The Rc of SARS-CoV-2 with the inflammatory response is smaller than the original reproduction number R0 without the inflammatory response. The addition of inflammatory responses changes the basic reproduction number R0 to Rc. It shows that if Rc < R0 < 1, the infection-free equilibrium of the model is globally asymptotically stable; if Rc < 1 < R0, the infected equilibrium without inflammatory is globally asymptotically stable, if 1 < Rc < R0, the infected equilibrium with inflammatory is globally asymptotically stable.
Rc < R0 implies that the inflammatory responses would decrease the rate of SARS-CoV-2 infection, which is beneficial to the body health. However, the infected equilibrium changes to two styles, infected equilibrium without inflammatory E1 and infected equilibrium with inflammatory E*. Different parameters, σI and σT, determine different E*. If σT is so large that inflammatory cells attack healthy cells more strongly, with lower T*, the clinical symptoms caused by pneumonia are more intense, which is an important cause of COVID-19 death. However, the activation of inflammatory cells are never changed the value of Rc by σI and σT, but changed by γ. It is an important result to give some help to understand the disease mechanism of SARS-CoV-2 in vivo and then give some advice to the diagnosis and treatment of COVID-19.
Acknowledgment
This work is supported by the National Natural Science Foundation of China, 11771044.
References
- (2019) Coronavirus disease (COVID-19) pandemic. World Health Organization.
- B Tang, X Wang, Qian Li, et al. (2020) Estimation of the transmission risk of the 2019-ncov and its implication for public health interventions. J Clin Med 9: 462.
- Joseph T Wu, K Leung, Gabriel ML (2020) Nowcasting and forecasting the potential domestic and international spread of the 2019-ncov outbreak originating in Wuhan, China: A Modelling study. Lancet 395: 689-697.
- L Ying, AA Gayle, WS Annelies, et al. (2020) The reproductive number of covid-19 is higher compared to SARS coronavirus, J Travel Med 27: 21.
- NS Chen, M Zhou, X Dong, et al. (2020) Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A Descriptive study. Lancet 395: 507-513.
- MA Nowak, CR Bangham (1996) Population dynamics of immune responses to persistent viruses. Science 272: 74-79.
- HL Smith, PD Leenheer (2003) Virus dynamics: A global analysis. Siam J Appl Math 63: 1313-1327.
- Korobeinikov (2004) Global properties of basic virus dynamics models. Bulletin of Mathematical Biology 66: 879-883.
- X Wang, A Elaiw, X Song (2012) Global properties of a delayed hiv infection model with CTL immune response. Applied Mathematics and Computation 218: 9405-9414.
- R Kumara, G Clermont, Y Vodovotz, et al. (2004) The dynamics of acute inflammation. J Theor Biol 230: 145-155.
- H Thieme (1993) Persistence under relaxed point-dissipativity (with application to an endemic model). SIAM J Math Anal 24: 407-435.
- L Han, A Pugliese (2009) Epidemics in two competing species. Nonlinear Analysis: Real World Applications 10: 723-744.
- Chentong Li, Jinhu Xu, Jiawei Liu, et al. (2020) The within-host viral kinetics of Sars-Cov-2. Mathematical Biosciences and Engineering 17: 2853-2861.
- F Pan, Tianhe Ye, Shan Gui, et al. (2020) Time course of lung changes on chest during recovery from 2019 novel coronavirus (covid-19). Radiology 295: 715-721.
Corresponding Author
Fangyuan Chen, School of Mathematical Sciences, Beijing Normal University, Beijing, 100875, China.
Copyright
© 2020 Chen F, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.