Journal of Fluid Dynamics

Thermal Radiation, Chemical Reaction and Viscous Dissipation Effects on MHD Mixed Convection Flow of Micro Polar Fluid with Stretching Surface in the Presence of Heat Generation/Absorption

Abstract

Numerical and theoretical analysis of MHD mixed convection flow of micropolar fluid with stretching surface in the presence of thermal radiation, chemical reaction, viscous dissipation, and heat generation/absorption has been studied. The governing nonlinear differential equations of momentum, angular velocity, energy and concentration are converted into ordinary differential equations using similarity transformations which are solved numerically. The dimensionless governing equations are solved using Runge-Kutta- Fehlberg fourth fifth order along with shooting method. The effect of physical parameters viz., micropolar parameter, unsteadiness parameter, thermal buoyancy parameter, concentration buoyancy parameter, Hartmann number, spin gradient viscosity parameter, micro inertial density parameter, thermal radiation parameter, Prandtl number, Eckert number, heat absorption or generation parameter, Schmidt number and chemical reaction parameter on flow variables viz., velocity of micropolar fluid, microrotation, temperature and concentration has been analyzed and discussed graphically. Furthermore, computational values of local skin friction coefficient, local wall coupled coefficient, local Nusselt number and local Sherwood number for different values of parameters have been investigated.

Keywords

Thermal radiation, Chemical reaction, Viscous dissipation, Heat absorption/generation, Similarity transformation

 Introduction

Micropolar fluid belongs to a class of micro fluids which exhibit both micro rotational effect and micro inertia with non-symmetric stress tensor. Micropolar fluid consists of large amount of rigid, randomly oriented or spherical particles suspended in a viscous medium which move along with micro-rotations. Liquid crystals, colloidal fluids, polymeric suspension, animal blood are some examples of Micropolar fluid. Micropolar fluid has wide application in engineering and science Viz., human blood, plasma, sediment in rivers, drug suspension in pharmacology, liquid crystals, bio fluid mechanics, blood vessel and lubrication technology. Furthermore, micropolar fluid includes application in lubrication theory, boundary layer theory, shortwave for heat conducting fluids, hydrodynamics of multi component media, magnetohydrodynamics and biological fluid modeling. Dynamics of micropolar fluid have significant applications in arterial blood flow, cardiovascular and cervical flows.

Eringen [1] introduced the model of micropolar fluid. In this model the fluid consists of rigid, randomly oriented suspended in viscous medium where the deformation of particle is ignored. Micropolar fluid exhibits microscopic effect which arises from the local structure and micro motion of fluid elements. Ariman, Turk and Sylvester [2] studied micro continuum fluid mechanics with several applications in physiological fluid flows. Philip and Chandra [3] investigated peristaltic transport of simple micro fluids which accounts microrotation and micro stretching of particles contained in a small volume of elements using long wavelength approximation. Giraja Devi and Devanatan [4] examined the peristaltic transport of micropolar fluid in a laboratory frame of reference. Hiremath [5] studied flow of micropolar fluid through a channel with injection. Gorla, Takhar and Slaouti [6] examined combine effects of buoyancy and magnetic forces of an electrically conducting micropolar fluid along hot vertical plate. Bhargava, Kumar and Takhar [7] studied the influence of magnetic field and temperature dependent heat source on micropolar fluid between two parallel plates. B. Zigta and P.R.Koya [8] studied the effect of MHD on a free convection oscillatory Couette flow when the temperature and concentration oscillate with time in the presence of the thermal radiation and chemical reaction. B. Zigta [9] studied the effect of thermal radiation, chemical reaction and viscous dissipation on MHD flow. B. Zigta [10] investigated thermal radiation, chemical reaction, viscous and Joule dissipation effects on MHD flow embedded in a porous medium.

The influence of density variation within the micropolar fluid leads to temperature and concentration difference between the surface and the fluid. As a result, both mass and heat transfer is affected by buoyancy force which is known as free convection. The combined effect of free and forced convection becomes important due to its application in industrial and engineering viz., food process industry, thermal insulation, heat exchangers, oil extraction and ground water flow. B. Zigta [11] examined mixed convection on MHD flow with thermal radiation, chemical reaction and viscous dissipation embedded in a porous medium. B. Zigta [12] studied effect of thermal radiation and chemical reaction on MHD flow of blood in stretching permeable vessel. Sing, Roy, and Ravindran [13] examined the behavior of unsteady mixed convection flow an incompressible viscous fluid over a vertical wedge with constant suction or injection. Zueco, Eguia, Abd El-Aziz, Collazo and Patino [14] studied unsteady free convection flow of MHD micropolar fluid through two parallel infinite porous vertical plates. Abd El-Aziz [15] analyzed unsteady mixed convection flow of a micropolar fluid adjacent to a heated vertical surface along with viscous dissipation and buoyancy force. Hussain, Ashraf, Nadeem and Khan [16] studied radiation effects on unsteady boundary layer flow of a micropolar fluid over a stretching permeable sheet.

The combined effect of heat and mass transfer problem of chemical reaction has many applications viz., biochemical systems, combustion, catalysts, process of drying, evaporation of a water body, and energy transfer in cooling surface. Chemical reactions are classified as homogeneous and heterogeneous process. A homogeneous reaction occurs uniformly in the whole fluid and heterogeneous reaction involves the production and consumption of reactant at different rate. A chemical reaction is said to be of first order if the rate of reaction is directly proportional to the concentration. Chemical reaction between foreign mass and the fluid can be applied in many engineering processes viz., polymer production, ceramics, and food processing. Oahimire and Olajuwon [17] examined heat and mass transfer effects on unsteady flow of a chemically reacting micropolar fluid over an infinite vertical porous plate. Das, Deka, Soundalgekar [18] considered the effects of a first order chemical reaction on the flow of past an impulsively started infinite vertical plate with constant heat flux and mass transfer.

Heat transfer in the fluid flow with stretching surface has attracted many scholars due to its wide applications in industrial and engineering processes viz., metal spinning, paper production, polymer extrusion. The fore cited work in this area was first made and the boundary layer flow from a linearly stretched plate has been studied Crane et al. [19]. Bhargava, Kumar and Takhar [20] obtained a finite element solution for the mixed convection micropolar fluid flow in a porous stretching sheet with suction. Eldabe and Ouaf [21] studied heat and mass transfer flow of a micropolar fluid past a stretching surface with Ohmic heating and viscous dissipation. Pal, Mandal and Vajravelu [22] analyzed the effects of thermal radiation and viscous dissipation on mixed convection of nanofluid over a nonlinear stretching or shrinking sheet. Mahmoud and Waheed [23] examined heat generation and absorption effects on MHD flow of micropolar fluid through a stretching surface. Grzegorz [24] has been mentioned micropolar fluid theory can be applied to model hip joint, cerebral spinal fluid and different problems in lubrication thus references about modeling and application of micropolar fluid. Kai-Long Hsiao [25] investigated to promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Kai-Long Hsiao [26] examined micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Kai-Long Hsiao [27] studied combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects.

Khilap Singh and Manoj Kumar [28] have been studied the effect of thermal radiation on mixed convection flow of a micropolar fluid of unsteady stretching surface in the presence of viscous dissipation and heat generation/ absorption. In this study the effects of Lorentz force and chemical reaction have not been considered.

The main objective of this paper is to study thermal radiation, chemical reaction and viscous dissipation effects on MHD mixed convection flow of a micropolar fluid with stretching surface in the presence of heat generation/ absorption. Such study does not appear in scientific literature reviews.

Mathematical Formulation and Analysis of the Model

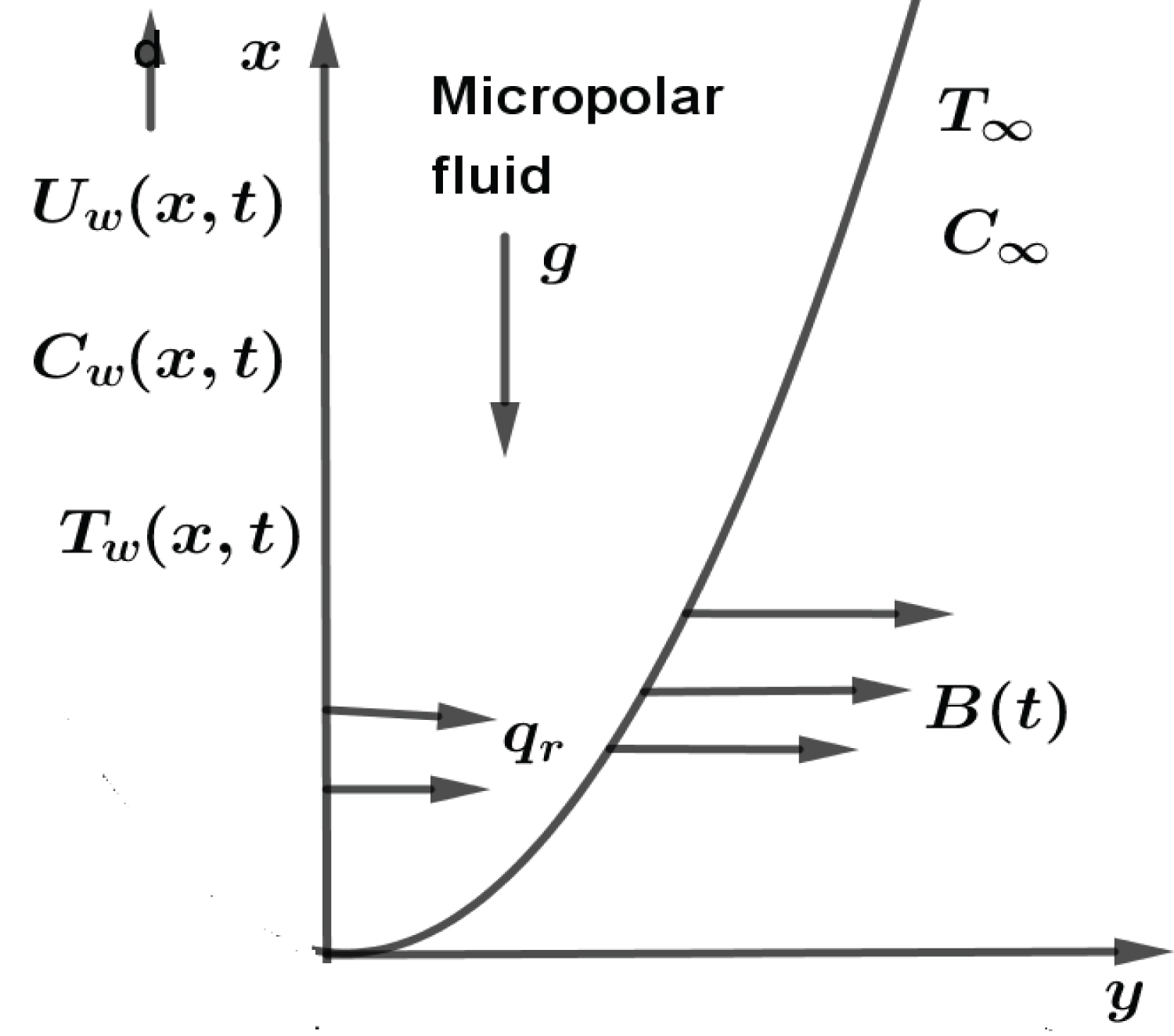
Consider unsteady, viscous, incompressible, mixed convection, electrically conducting micropolar fluid over elastic, impermeable stretching surface of vertical plate in the presence of thermal radiation, chemical reaction, viscous dissipation and heat generation/absorption. The x axis is taken in upward direction that is opposite to gravitational acceleration. The y axis is taken normal to the vertical plate. The origin is kept fixed in the fluid medium of ambient temperature $T_{\infty }$ and ambient concentration of solute $C_{\infty }$.

The flow configuration and the coordinate system are shown in Figure 1. The positive x axis is taken along the stretching sheet and the positive y axis is measured normal to the sheet in the outward direction towards the fluid. The velocity $U_w\left(x,t\right)$ reveals the elastic surface which is fixed at the origin is stretched by applying force in the positive upward direction and the effective stretching rate $\frac{ax}{1+ct}$ increases with time; the surface temperature ${{\rm T}}_W\left(x,t\right)$ of stretching surface varies with distance x and time t; the concentration of the fluid $C_w\left(x,t\right)$ depends on distance x and time t; both the surface temperature and concentration of the fluid depend on the situation if b is positive or negative results in both increment and decrement respectively; and time dependent chemical reaction parameter $k_r\left(t\right)$ takes the following form.

$$\begin{array}{l}{U}_W\left(x,t\right)=\frac{ax}{1-ct},T_w\left(x,t\right)=T_{\infty }+\frac{bx}{{\left(1-ct\right)}^2},\\ C_w\left(x,t\right)=C_{\infty }+\frac{bx}{{\left(1-ct\right)}^2},k_r\left(t\right)=\frac{k_{{\rm O}}}{D\left(1-ct\right)}\left(1\right)\end{array}$$

Where a, b, c and k₀ are the constants such that $a>0,b\ge 0,c\ge 0$ and $t<c^{-1}$. Time dependent magnetic field intensity is denoted $B\left(t\right)=\frac{B_o}{\sqrt{\left(1-ct\right)}},B_0$ is magnetic field strength at t=0 and $K_r(t)$ is chemical reaction rate of the fluid.

The expressions $U_w\left(x,t\right)$, $T_w\left(x,t\right)$ and $C_w\left(x,t\right)$ are valid if $ct<1$ unless $c=0$. Furthermore, the velocity of the stretching sheet $U_w\left(x,t\right)$ describes the elastic surface which is fixed at the origin is stretched by applying force in the positive x direction and the rate of stretching surface increases with time. The surface temperature $T_w\left(x,t\right)$ of the stretching sheet reveals the situation in which the temperature increases if $b>0$ and decreases if $b<0$. The amount of ambient temperature $T_{\infty }$ along the stretching sheet increases or decreases with time and the concentration of micropolar fluid $C_w\left(x,t\right)$ describe the situation in which the concentration increases if $b>0$ and decrease if $b<0$.

To derive the governing equations of the model the following assumptions are made:

1. All fluid properties are constant except the influence of the density variation with temperature and concentration in the body force term.

2. The flow of the fluid is unsteady, laminar, incompressible, viscous, electrically conducting, non-Newtonian, thermal radiating and chemical reacting.

3. The Eckert number and magnetic Reynolds numbers are small so that the induced magnetic field of the fluid is negligible.

4. The magnetic field is time dependent which acts in the direction transverse to the vertical plate.

5. The effect of viscous dissipation is considered in the energy equation.

6. There is a first order chemical reaction between the diffusion concentration and the fluid.

7. Thermal radiation, chemical reaction and viscous dissipation are taken into consideration.

Based on these assumptions the governing equations of the conservation of mass, momentum, angular velocity, energy and concentration take the following form:

$$\frac{\partial u}{\partial t}+\frac{\partial v}{\partial y}=0\left(2\right)$$

$$\begin{array}{l}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left(\frac{\mu +k}{\rho }\right)\frac{{\partial }^{2}u}{\partial y^2}+\frac{k}{\rho }\frac{\partial N}{\partial y}+g\beta \left(T-T_{\infty }\right)+\\ g{\beta }_c\left(C-C_{\infty }\right)-\frac{\sigma B^2\left(t\right)u}{\rho },\left(3\right)\end{array}$$

$$\frac{\partial N}{\partial t}+u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}=\left(\frac{\gamma }{\rho j}\right)\frac{{\partial }^{2}N}{\partial y^2}-\frac{k}{\rho j}\left(2N+\frac{\partial u}{\partial y}\right),\left(4\right)$$

$$\begin{array}{l}\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\left(\frac{\mu +k}{\rho C_p}\right){\left(\frac{\partial u}{\partial y}\right)}^2-\frac{1}{\rho C_p}\frac{\partial q_r}{\partial y}+\\ \left(\frac{Q_0}{\rho C_p}\right)\left(T-T_{\infty }\right),\left(5\right)\end{array}$$

$$\frac{\partial c}{\partial t}+u\frac{\partial c}{\partial x}+v\frac{\partial c}{\partial y}=D\frac{{\partial }^{2}c}{\partial y^2}-k_{\gamma }\left(C-C_{\infty }\right).\left(6\right)$$

Equations (2) - (6) govern the present model. Here u denotes velocity of the fluid flow along x axis and v represents transverse velocity of fluid flow. Furthermore, $\mu ,\rho$ and $k$ denotes dynamic viscosity, density and vortex viscosity of the fluid respectively. $\beta$ is the volumetric coefficient of thermal expansion, ${\beta }_c$ is the volumetric coefficient of concentration expansion, v is kinematic viscosity, j is micro inertia density, $\gamma$ is the spin gradient viscosity, $N$ is the component of microrotation whose direction of rotation lies in the $x-y$ plane, g is the gravitational acceleration, $q_r$ is the radiative heat flux, $Q_0$ is the heat generation $\left(>0\right)$ or absorption $\left(<0\right)$ coefficient, $Q_0\left(T-T_{\infty }\right)$ is the volumetric rate of heat generation/absorption within the fluid, $C_p$ is the specific heat capacity at constant pressure, $\alpha$ is thermal diffusivity, D is molecular diffusivity, $\sigma$ is the electrical conductivity and $k_r$ is chemical reaction parameter.

The boundary conditions for the model has the form

$$u=U_w,v=0,N=0,T=T_w,C=C_{w}aty=0\left(7\right)$$

$$u\to 0,N\to 0,T\to T_{\infty },C\to C_{\infty }asy\to \infty .\left(8\right)$$

The Rosseland approximation for radiative heat flux [Raptis, 1998] is given by

$$q_r=\left(\frac{-4{\sigma }^{*}}{3k_s}\right)\left(\frac{\partial T^4}{\partial y}\right)\left(9\right)$$

In (9), the parameters ${\sigma }^{*}$ and $k_s$ represent the Stefan Boltzmann constant and the Rosseland mean absorption coefficient, respectively.

Assuming that the temperature difference in the fluid flow is sufficiently small, $T^4$ in Eq. (9) can be expressed as a linear function of $T_{\infty }$ using Taylor series expansion. Taking the Taylor series expansion of $T^4$ and neglecting terms with higher powers have the following form

$$T^4\cong 4T_{\infty }{}^{3}T-3T_{\infty }{}^4\left(10\right)$$

Using equation (9) and (10), Eq. (5) reduces

$$\begin{array}{l}\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\left(\frac{\mu +k}{\rho C_p}\right){\left(\frac{\partial u}{\partial y}\right)}^2+\\ \left(\frac{1}{\mu C_p}\right)\left(\frac{16{\sigma }^{*}{T}_{\infty }{}^3}{3k_s}\right)\left(\frac{{\partial }^{2}T}{\partial y^2}\right)+\left(\frac{Q_0}{\rho C_p}\right)\left(T-T_{\infty }\right)\left(11\right)\end{array}$$

Non-Dimensionalization of the Model

In order to find similarity solution of the problem the following non dimensional variables are introduced [Ludlow, Clarkson and Bassom, 2000]

$$\begin{array}{l}\eta =\sqrt{\frac{a}{v\left(1-ct\right)}}y,\psi =\sqrt{\frac{va}{1-ct}}xf\left(n\right),N=\sqrt{\frac{a^3}{v{\left(1-ct\right)}^3}}xg\left(\eta \right),\\ T=T_{\infty }+\frac{bx}{{\left(1-ct\right)}^2}\theta \left(\eta \right),\end{array}$$

$$C=C_{\infty }+\frac{bx}{{\left(1-ct\right)}^2}\varphi \left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\varphi \left(\eta \right)=\frac{c-c_{\infty }}{c_w-c_{\infty }},\left(12\right)$$

The continuity equation (2) satisfies the stream function defined by

$$u=\frac{\partial \psi }{\partial y}=U_w{f}^{\text{'}}\left(\eta \right),\left(13\right)$$

$$v=-\frac{\partial \psi }{\partial x}=-\sqrt{\frac{va}{1-ct}}f\left(\eta \right),\left(14\right)$$

Substituting Eq. (12) into equations (3) - (6) the following set of ordinary differential equations are obtained

$$\left(1+k_c\right)f\text{'}\text{'}\text{'}+ff\text{'}\text{'}-{\left(f\text{'}\right)}^2-A\left(f\text{'}+\frac{n}{2}f\text{'}\text{'}\right)+k_{c}g\text{'}+\tau \theta +\chi \varphi -Mf\text{'}=0\left(15\right)$$

$$\lambda g"+gf\text{'}-g\text{'}f-A\left(\frac{3}{2}g+\frac{\eta }{2}g\text{'}\right)-k_c\zeta \left(2g+f"\right)=0,\left(16\right)$$

$$\left(\frac{3R+4}{3\mathrm{Pr}R}\right)\theta "+f\theta \text{'}-f\text{'}\theta -A\left(2\theta +\frac{\eta }{2}\theta \text{'}\right)+Ec\left(1+kc\right){\left(f"\right)}^2+\Gamma \theta =0\left(17\right)$$

$$\varphi "+Sc\left(f\text{'}\varphi -f\varphi \text{'}\right)-ASc\left(\frac{1}{2}\eta \varphi \text{'}+2\varphi \right)-K_r\varphi =0\left(18\right)$$

In equations (15) - (18), $k_c,A,\tau ,\chi ,M,\lambda ,\zeta ,R,\mathrm{Pr},{\rm E}c,\Gamma ,Sc$ and $k_r$ denotes micropolar parameter, unsteadiness parameter, thermal buoyancy parameter, concentration buoyancy parameter, Hartmann number, spin gradient viscosity parameter, microinertial density parameter, thermal radiation parameter, Prandtl number, Eckert number, heat absorption or generation parameter, Schmidt number and chemical reaction parameter represented by

$$\begin{array}{l}kc=\frac{k}{\mu },A=\frac{c}{a},\Gamma =\frac{gBb}{a^2},\chi =\frac{g{B}_{c}b}{a^2},M=\frac{\sigma B^2}{\rho a},\lambda =\frac{\gamma }{\mu j},\zeta =\frac{v\left(1-ct\right)}{ja},\\ R=\frac{k{k}_g}{4{\sigma }^{*}{T}_{\infty }^3}.\mathrm{Pr}=\frac{\mu Cp}{\kappa },Ec=\frac{U_w^2}{Cp\left(T_W-T\infty \right)},\Gamma =\frac{Q_0}{\mu Cp},Sc=\frac{v}{D}andkr=\frac{k_0}{D\left(1-c\Gamma \right)}\end{array}$$

The corresponding boundary conditions (7) - (8) take the form

$$f\left(n\right)=0,f\text{'}\left(\eta \right)=1,g\left(\eta \right)=0,\theta \left(\eta \right)=1and\varphi \left(\eta \right)=1at\eta =0,\left(19\right)$$

$$f\text{'}\left(\eta \right)=0,g\left(\eta \right)=0,\theta \left(\eta \right)=0and\varphi \eta =0as\eta \to \infty \left(20\right)$$

The most important physical quantities for this model problem are the local skin friction coefficient $C_f$ the local wall coupled coefficient $C_{wx}$, the local Nusselt number $N{u}_x$ and Sherwood number $S{h}_x$ defined as:

$$C_f=\frac{2}{\rho U_W^2}\left[\left(\mu +k_c\right){\left(\frac{\partial u}{\partial y}\right)}_{y=0}+k{\left(N\right)}_{Y=0}\right]=2\left(1+k_c\right)\frac{1}{\sqrt{{\mathrm{Re}}_x}}{f}^n\left(0\right)\left(21\right)$$

$$C_{wx}=\gamma {\left(\frac{\partial N}{\partial y}\right)}_{y=0}=\gamma U_W\left(\frac{a}{\nu \left(1-ct\right)}\right)g\text{'}\left(0\right)\left(22\right)$$

$$N{u}_x=\left(-\frac{x}{T_W-T_{\infty }}\right){\left(\frac{\partial T}{\partial y}\right)}_{y=0}=-\sqrt{{\mathrm{Re}}_x}\theta \text{'}\left(0\right)\left(23\right)$$

$$S{h}_x=\frac{-x}{D(C_W-C_{\infty })}{\left(\frac{\partial c}{\partial y}\right)}_{y=0}=-\sqrt{{\mathrm{Re}}_x}\varphi \text{'}\left(0\right)\left(24\right)$$

Here in equations (23) - (24) ${\mathrm{Re}}_x$ denotes the local Reynolds number represented by ${\mathrm{Re}}_x=\frac{xUw}{\nu }$ which depend on stretching velocity.

Numerical Solution to the Problem

The nonlinear ordinary differential equations (15) - (18) together with the boundary conditions (19) - (20) are solved numerically using Runge-Kutta- Fehlberg fourth fifth order along with shooting method. Convenient values of the boundary conditions at $\eta =\infty ,$ $f\text{'}\left({\eta }_{\infty }\right)=0,$ $g\text{'}\left({\eta }_{\infty }\right)=0,$ $\theta \text{'}\left({\eta }_{\infty }\right)=0,$ and $\varphi \text{'}\left({\eta }_{\infty }\right)=0$ are satisfied. The maximum values of ${\eta }_{\infty }$ is determined when the values of the unknown boundary condition at $\eta =0$ does not change with an error less than 10^-3. Computations were done using computer language MATLAB code for different values of ${\eta }_{\infty }$ and step sizes $\Delta \eta$ are used. It can be observed that there is no change in velocity, angular velocity, temperature and concentration for values of $\eta >7$. Therefore in the present study the maximum value ${\eta }_{\infty }=7$ and step size $\Delta \eta =0.001$ are taken. To solve the problem the nonlinear differential equations are converted in to nine first order linear ordinary differential equations. There are five initial conditions at $\eta =0$ and four boundary conditions $\eta =\infty$. To find the solution of the problem there are four more initial conditions at $\eta =0$, the values of $f\text{'}\text{'}$, $g\text{'}$, $\theta \text{'}$ and $\varphi \text{'}$ these conditions are determined by shooting technique. Then the solutions of the problem are solved using Runge-Kutta- Fehlberg fourth fifth order.

First higher order nonlinear differential equations (15) - (18) are converted into simultaneous linear differential equations of first order using

$$\begin{array}{l}{y}_1=f,y_2=f\text{'},y_3=f",y_4=g,y_5=g\text{'},y_6=\theta ,y_7=\theta \text{'},y_8=\varphi ,y_9=\varphi \text{'}\\ y_1^{\text{'}}=y_2\\ y^{\text{'}}{}_2=y_3\\ y_3^{,}=\left(\frac{1}{1+k_c}\right)\left[-y_1{y}_3+{\left(y_2\right)}^2+A\left(y_2+\frac{\eta }{2}{y}_3\right)-k_c{y}_5-\tau y_6-\chi y_7+M{y}_2\right]\\ y{\text{'}}_4=y_5\\ y{\text{'}}_5=\frac{1}{\lambda }\left[y_5{y}_1-y_4{y}_2+A\left(\frac{3}{2}{y}_4+\frac{\eta }{2}{y}_5\right)+k_c\zeta \left(2y_4+y_3\right)\right]\\ y{\text{'}}_6=y_7\\ y{\text{'}}_7=\left(\frac{-3PrR}{3R+4}\right)\left[y_2{y}_6-y_1{y}_7+A\left(2y_6+\frac{\eta }{2}{y}_7\right)+Ec\left(1+k_C\right){\left(y_3\right)}^2-\Gamma y_6\right]\\ y{\text{'}}_8=y_9\\ y{\text{'}}_9=-Sc\left(y_2{y}_8-y_1{y}_9\right)+ASc\left(2y_8+\frac{\eta }{2}{y}_9\right)+k_r{y}_8)\end{array}$$

The corresponding boundary conditions

$$\begin{array}{l}{y}_1\left(\eta \right)=0,y_2\left(\eta \right)=1,y_4\left(\eta \right)=0,y_6\left(\eta \right)=1,y_8\left(\eta \right)=1\\ y_3\left(\eta \right)=m,y_5\left(\eta \right)=n,y_7\left(\eta \right)=l,y_9\left(\eta \right)=w\end{array}$$

Where $m,n,l$ and w are unknown to be computed using shooting technique to solve numerically.

Simulation Study of the Model

Thermal radiation, chemical reaction and viscous dissipation effects on MHD mixed convection flow of microplar fluid with streching surface in the presence of heat generation or absorption have been studied. The governing nonlinear partial differential equations of micropolar fluid are converted in to simulataneous set of ordinary differential equations using similarity transformations which can be solved numerically using Runge-Kutta- Fehlberg fourth fifth-order along with shooting technique.

The effects of physical parameters Viz., micropolar parameter, Hartmann number, unsteadiness parameter, thermal buoyancy parameter, concentration buoyancy parameter, micro inertial density parameter, spin inertial density parameter, Prandtl number, thermal radiation, heat generation, viscous dissipation parameter, chemical reaction parameter and Schmidt number on flow variables Viz., momentum, angular velocity, energy and concentration of micropolar fluid studied.

Graphical represntations of velocity profile for different values of micropolar parameter, Hartmann number, unsteadiness parameter, thermal and concentration buoyancy parameters; Microrotation profile for different values of micropolar parameter, unsteadiness parameter, micro inertial density parameter and spin inertial density parameter; Temperature profile for different values of micropolar parameter, unsteadiness parameter, Prandtl number, thermal radiation parameter, viscous dissipation parameter and heat absorption parameter. Furthermore, concentration profile for different values of unsteadiness parameter, chemical reaction parameter and Schmidt number has been presented.

Figure 2 presents the effect of micropolar parameter on velocity profile. The graph is drawn $f\text{'}$ versus $\eta$ representing dimensionless velocity along the vertical axis and dimensionless distance along the horizontal axis respectively. For particular value of micropolar parameter the value of micropolar fluid velocity starts from zero and increases as the value of dimensionless distance increases. From the simulation study it can be concluded that as micropolar parameter increases the velocity of micropolar fluid decreases. Since micropolar parameter describes the material property of micropolar fluid. Physiologically, this can be interpreted as stretching blood vessel exerts a resistive force on the flow of micropolar fluid. Thus an increment of micropolar parameter results in decrement of velocity of the fluid flow.

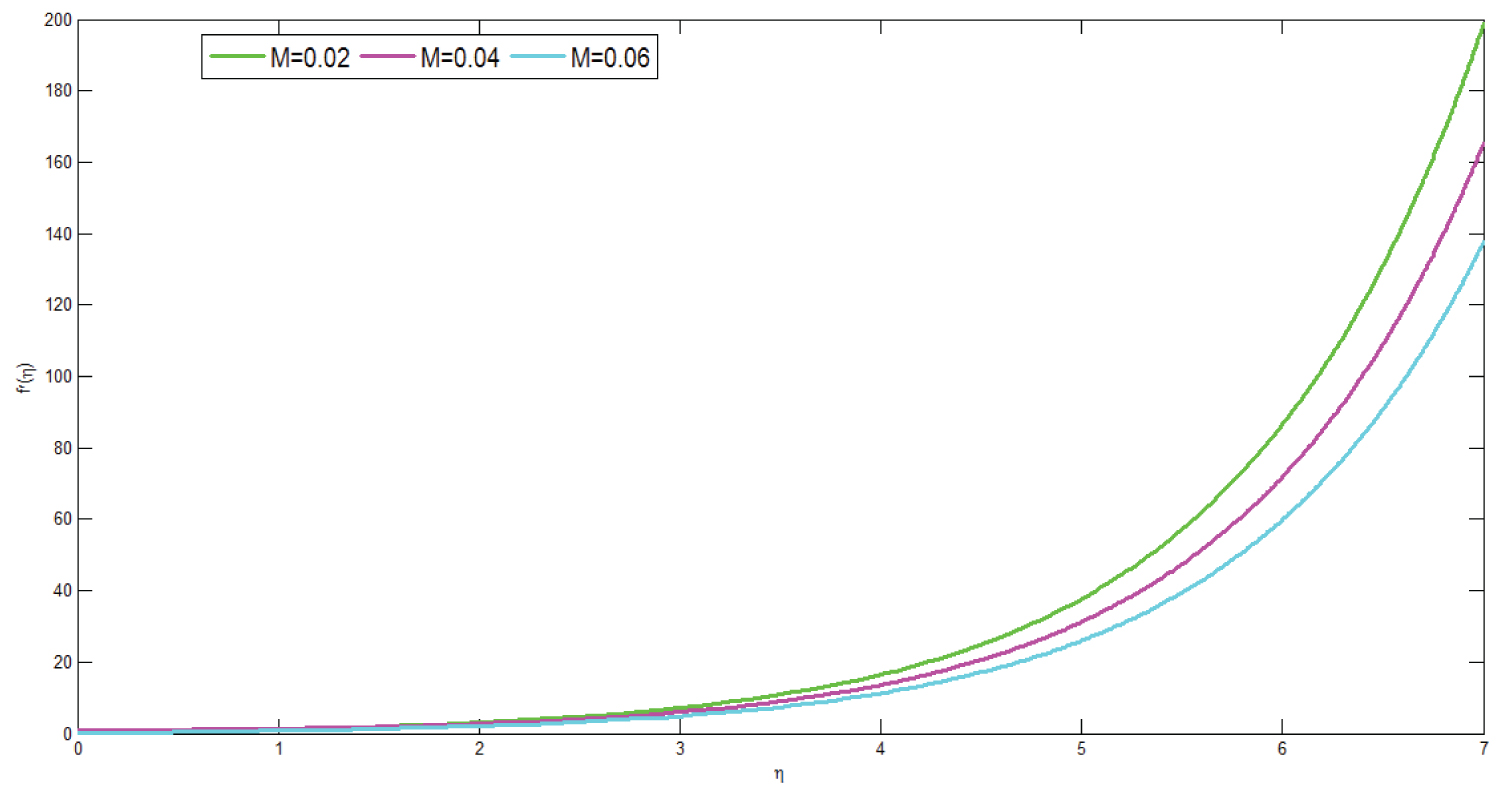
Figure 3 shows the effect of applied magnetic field on dimensionless velocity profile of micropolar fluid. The graph is plotted $f\text{'}$ versus $\eta$ for different values of dimensionless velocity against dimensionless distance respectively. From the Figure it can be observed that as the values of applied magnetic field increases the velocity of micropolar fluid decreases this occurs due to the Lorentz force which tends to resist the fluid flow and hence reduce the velocity of fluid flow.

Blood is considered as micropolar fluid because it accounts microrotation fluid suspension and micro inertia with non-symmetric stress tensor. Physiologically, this can be expressed as velocity of micropolar fluid in the blood vessel decreases due to red blood cells which contain high concentration of hemoglobin molecules. The influence of magnetic field causes red blood cells to flow in the direction parallel to the magnetic field. This results in an increment of concentration of red blood cells hence internal blood viscosity increases thus velocity of blood flow decreases.

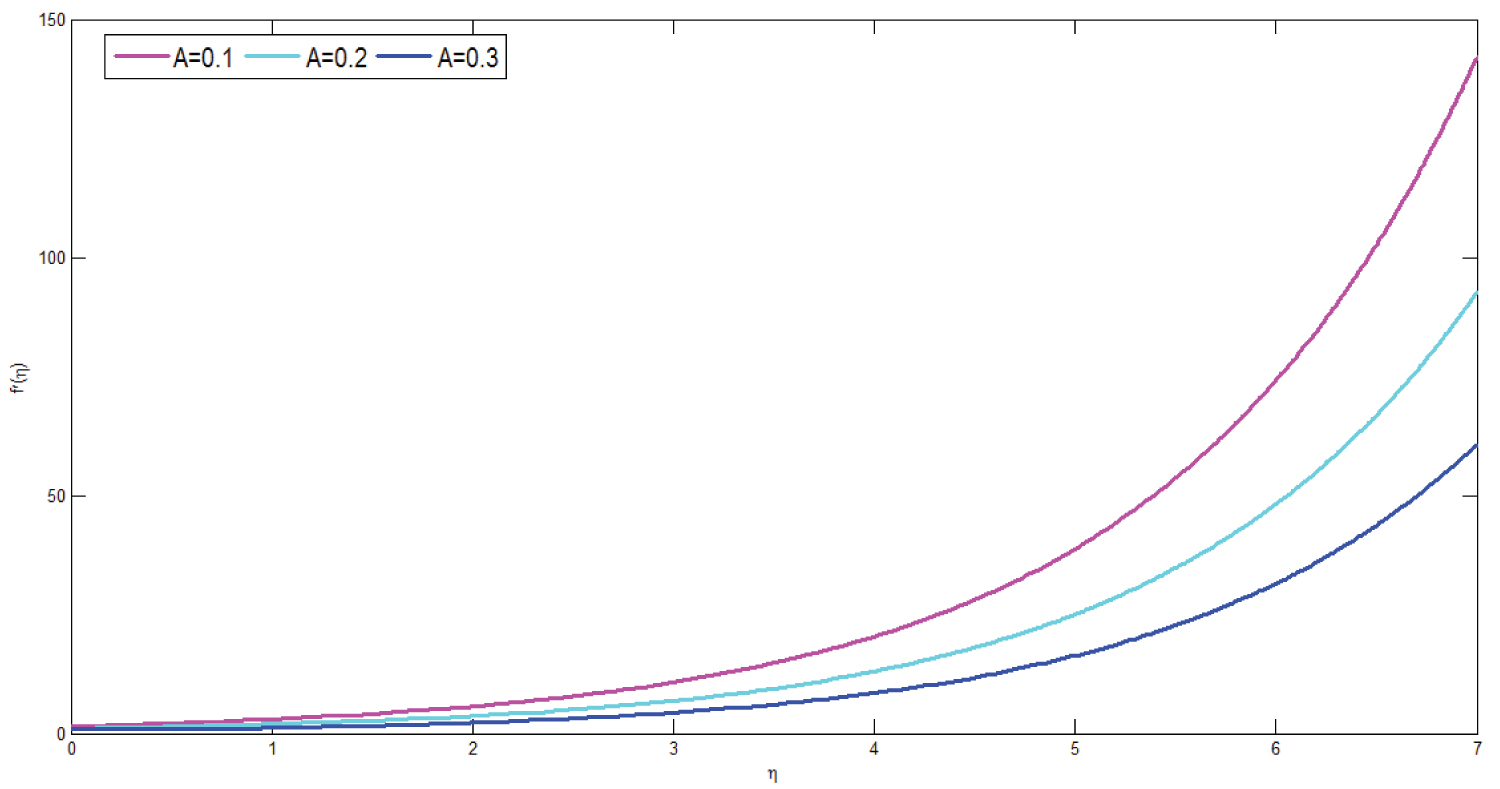
Figure 4 depicts the effect of unsteadiness parameter on velocity profile of the model. The graph is plotted $f\text{'}$ versus $\eta$ with dimensionless velocity and dimensionless distance respectively. For particular value of unsteadiness parameter the value of micropolar fluid velocity starts from zero and increases as the value of dimensionless distance increases. From the simulation results it can be deduced that as unsteadiness parameter increases the velocity flow of micropolar fluid decreases this causes reduction of momentum boundary layer. This means the unsteadiness parameter has retarding effect in momentum of boundary layer which opposes the flow due to the colloidal suspension property of the micropolar fluid. Physiologically, this can be interpreted as the flow of micropolar fluid with slip or no slip boundary layer of blood vessel increases unsteadiness parameter which results in decrement of velocity of the fluid flow.

Figure 5 presents the simulated result of thermal buoyancy parameter on velocity profile of the model. The graph is drawn versus representing dimensionless velocity against dimensionless distance respectively. From this study it can be concluded that as thermal buoyancy parameter increases the velocity flow of micropolar fluid decreases.

Physiologically, this can be described as micropolar fluid velocity decreases along the axis of the blood vessel the buoyancy force opposes the fluid flow by retarding the fluid in the boundary layer. Physically, this means cooling of the fluid or heating stretching surface. Furthermore, when micropolar fluid cooled there is decrement in thickness of the boundary layer which results in decrement of velocity of micropolar fluid.

Figure 6 shows the effect of concentration buoyancy parameter on velocity profile of the model. The graph is drawn $f\text{'}$ versus $\eta$ representing dimensionless velocity along the vertical axis and dimensionless distance along the horizontal axis respectively. From the simulation study it can be concluded that as the concentration buoyancy parameter increases the flow velocity of micropolar fluid decreases. This can be interpreted physiologically as micropolar fluid flow is retarded due to the effect of buoyancy which slows down the velocity of fluid flow.

Figure 7 presents the effect of micropolar parameter on microrotation profile of the model. The graph is plotted g versus $\eta$ denotes dimensionless angular velocity and dimensionless distance respectively. The simulation study shows an increment in micropolar parameter results in decrement of microrotation profile. Physiologically, this can be interpreted as an increment in blood viscosity results in decrement of microrotation flow this decrement is due to lose of energy in fluid particles.

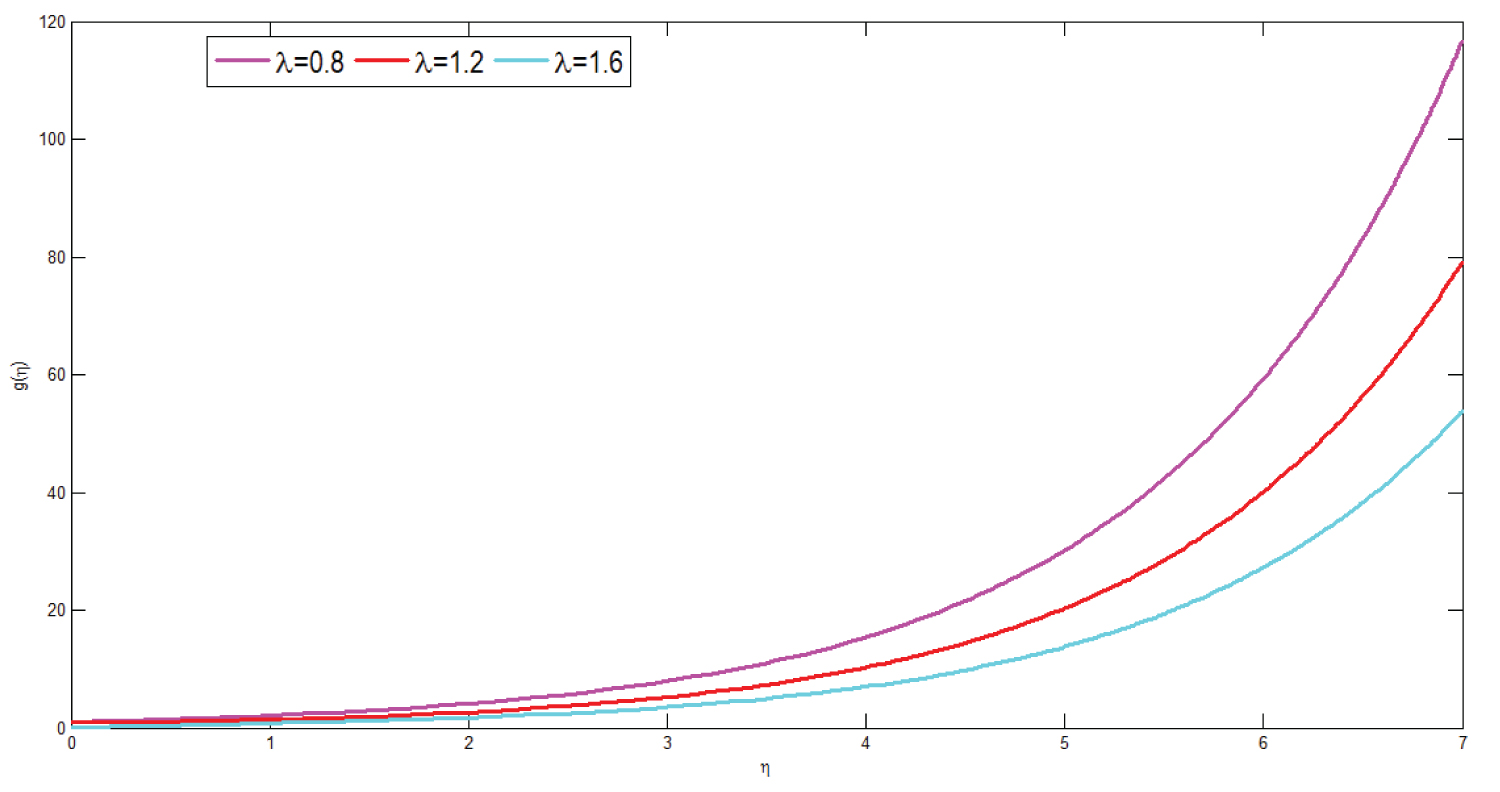
Figure 8 presents microrotation profile of the model for different values of unsteadiness parameter. The graph is plotted g versus $\eta$ denotes dimensionless angular velocity and dimensionless distance respectively. From the simulation study it can be concluded that an increment in unsteadiness parameter results in decrement of microrotation.

Figure 9 shows the influence of microinertial density parameter on microrotation profile. The graph is drawn g versus $\eta$ denoting dimensionless angular velocity along the vertical axis and dimensionless distance along the horizontal axis respectively. The result of the simulation study presents as the values of the microinertial density increases microrotational profile of micropolar fluid decreases.

Figure 10 presents the effect of spin gradient viscosity parameter on microrotation profile of the model. The graph is drawn g versus $\eta$ representing dimensionless angular velocity along the vertical axis and dimensionless distance along the horizontal axis respectively. From the simulation study it can be observed that an increment in the values of spin gradient viscosity parameter results in decrement of microrotational profile of micropolar fluid.

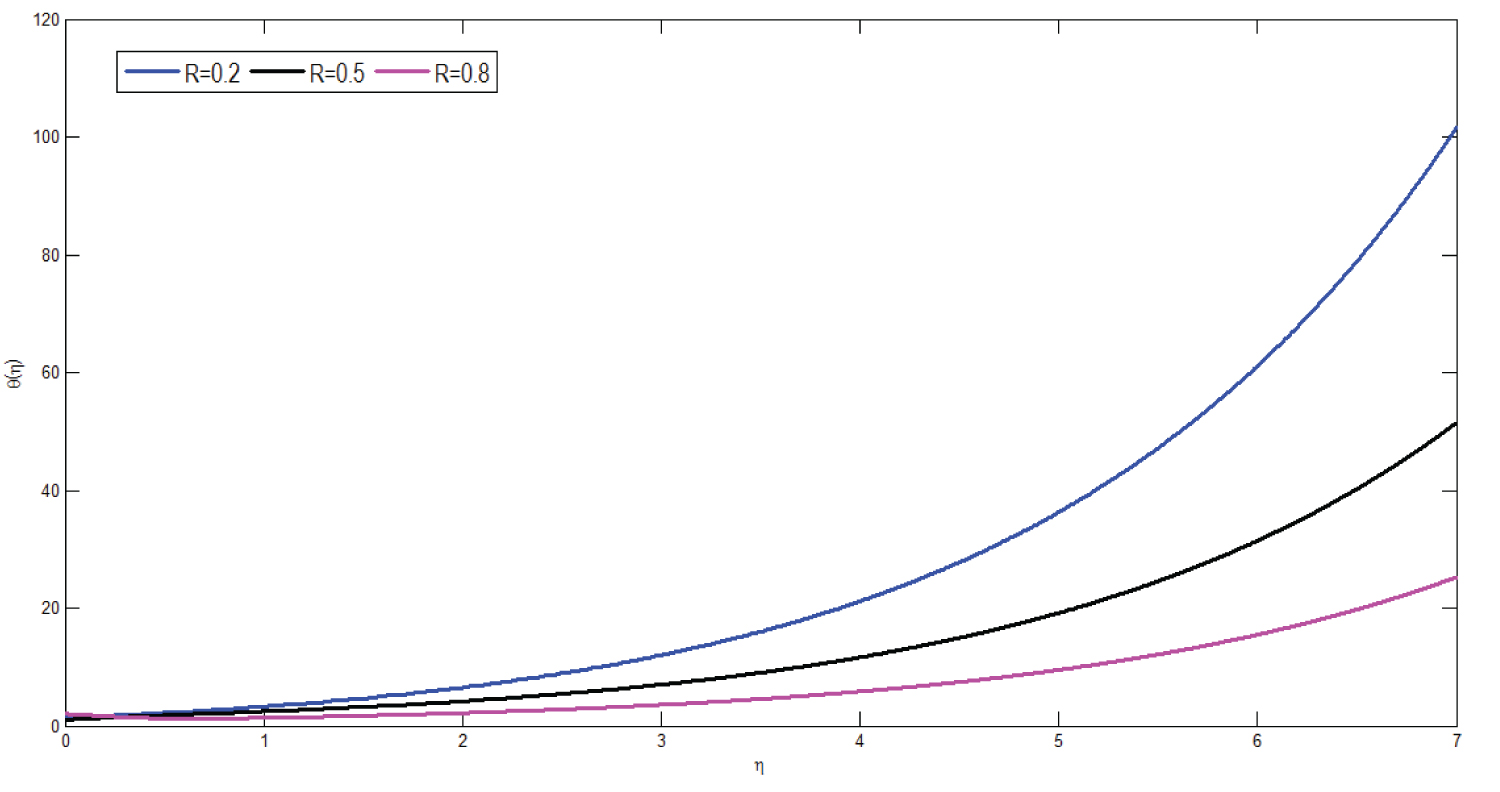
Figure 11 presents temperature profile of the model for different values of thermal radiation parameter. The graph is drawn $\theta$ versus $\eta$ denoting dimensionless temperature and dimensionless distance respectively. From the simulation study it can be observed that an increment in the values of thermal radiation parameter results in decrement of temperature profile of the model. Physiologically, this can be interpreted as thermal radiation increases micropolar fluid flow in arterial blood increases. This is due to the action of thermal radiation as heat generator with in boundary layer of the vessel. Therefore temperature of the boundary layer increases. Hence this enhances the effect of thermal buoyancy of body force which decreases temperature distribution of the micropolar fluid. Therefore, an increment of thermal radiation parameter results in decrement of temperature profile.

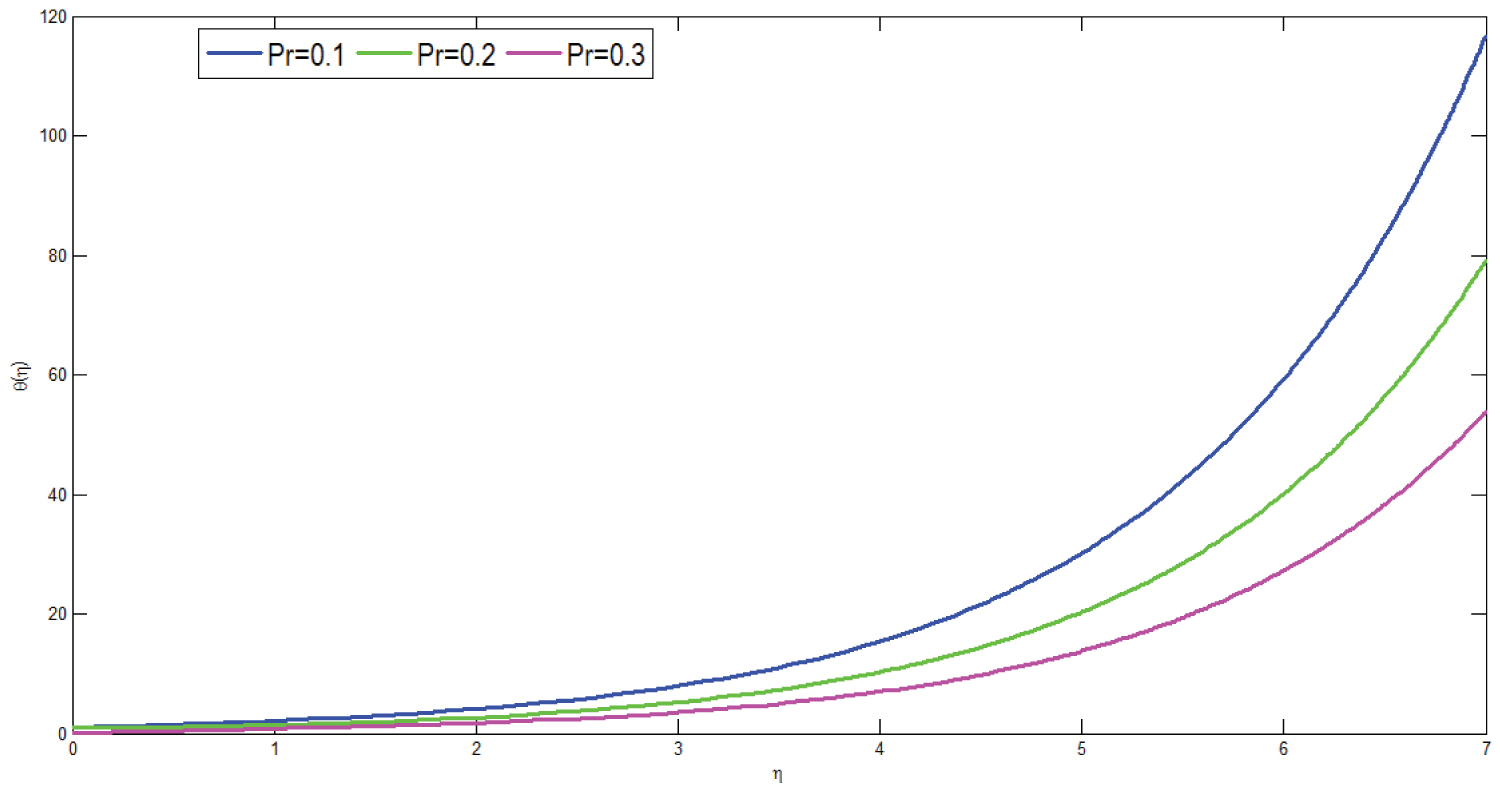
Figure 12 presents temperature profile of the model for different values of Prandtl number. The graph is drawn $\theta$ versus $\eta$ with dimensionless temperature and dimensionless distance respectively. From the simulated result it can be concluded that as Prandtl number increases temperature profile of the model decreases. This shows that an increment of Prandtl number implies decrement of thermal boundary layer. This can be expressed as thickness of thermal boundary layer reduces with an increment of Prandtl number. Physiologically, this can be interpreted as when micropolar fluid attains higher Prandtl number results in decrement of both thermal conductivity and heat conduction capacity. Consequently, thermal boundary layer thickness decreases hence heat transfer rate of blood vessel decreases. Therefore, an increment of Prandtl number results in decrement of temperature profile of the model.

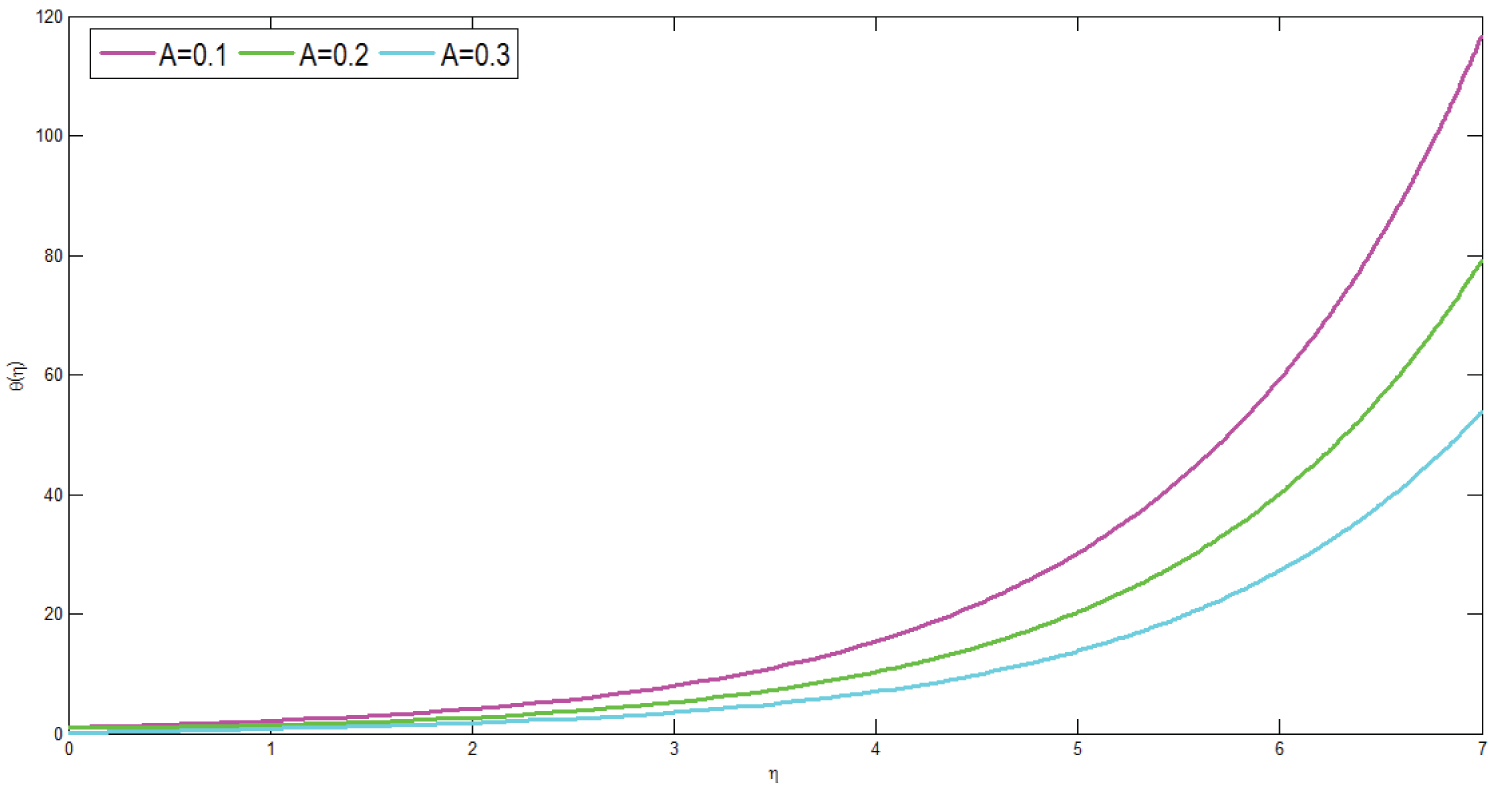
Figure 13 shows temperature profile of the model for different values of unsteadiness parameter. The graph is plotted $\theta$ versus $\eta$ representing dimensionless temperature along the vertical axis and dimensionless distance along the horizontal axis respectively. From the simulation study it can be observed that an increment in unsteadiness parameter results in decrement of temperature profile of the model. From this it can be concluded that the rate of heat transfer decreases with increment of unsteadiness parameter. Physiologically, this can be explained as in the presence or absence of slip or no slip boundary layer of blood vessel an increment in unsteadiness parameter results in decrement of temperature of the blood vessel.

Figure 14 presents the effect of micropolar parameter on temperature profile of the model. The graph is drawn $\theta$ versus $\eta$ with dimensionless temperature along the vertical axis and dimensionless distance along the horizontal axis respectively. From the simulation study it can be observed that an increment of micropolar parameter results in decrement of temperature profile. Physiologically, this can be expresses as decrement of heat transfer in the blood vessel results in an increment of micropolar parameter. For higher values of micropolar parameter there is decrement of thermal boundary layer this causes micropolar fluid to cool down. Since thermal energy is transferred from higher temperature to lower temperature there is decrement of heat transfer. Consequently, there is heat absorption in the blood vessel which results in decrement of temperature within the blood vessel.

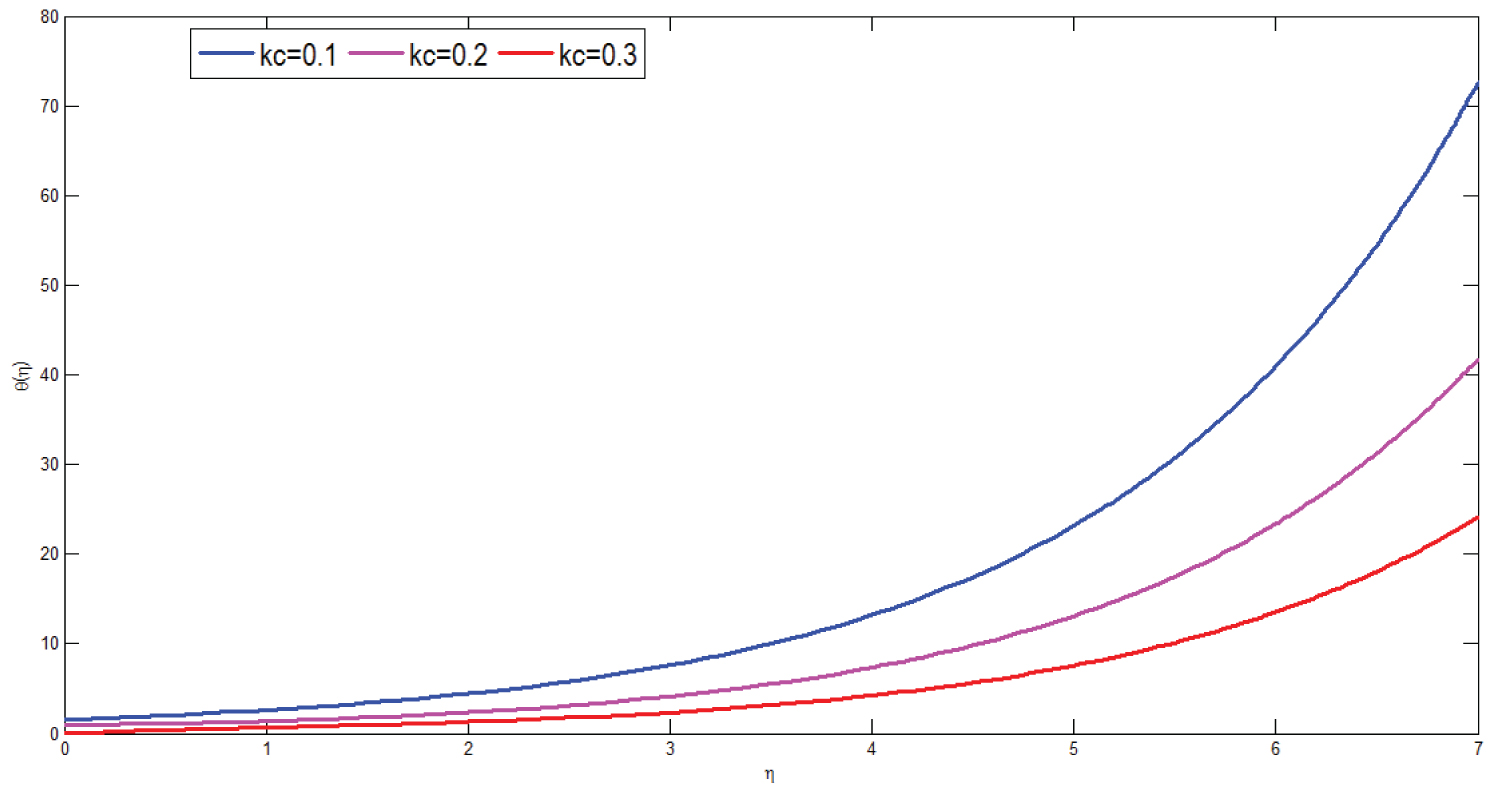
Figure 15 presents the effect of heat absorption parameter on temperature profile of the model. The graph is drawn $\theta$ versus $\eta$ with dimensionless temperature along the vertical axis and dimensionless distance along the horizontal axis respectively. From the simulation study it can be observed that an increment of heat absorption parameter results in decrement of temperature profile of the model. Heat absorption causes to decrease thermal boundary layer and the micropolar fluid becomes cooler. Physiologically, this can be described heat transfer is smaller along the stretching surface of the blood vessel this results in decrement of temperature. Hence this reduces radiation in the vessel which can be applied in therapeutic procedure of electromagnetic hyperthermia in treatment of cancer.

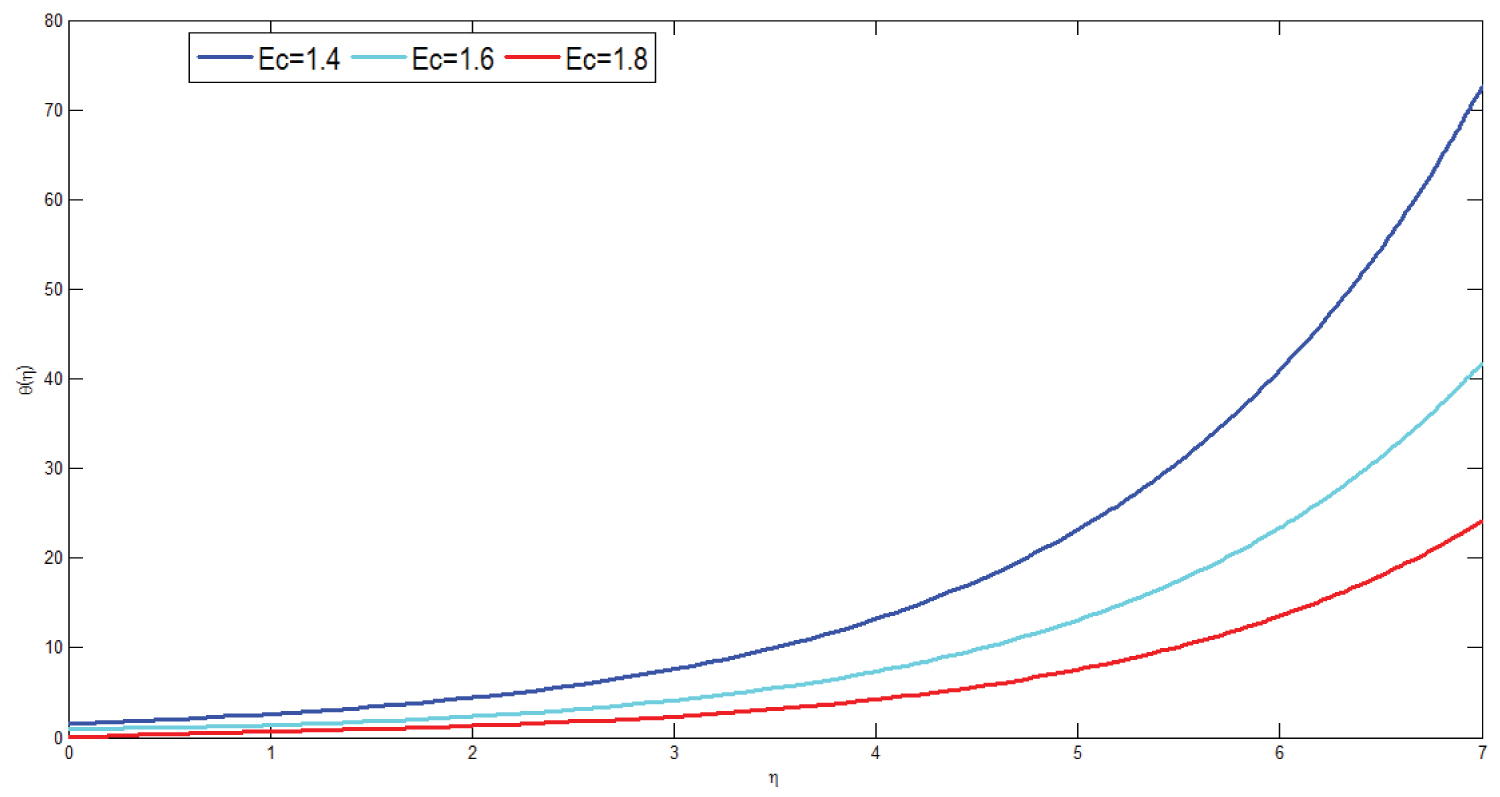
Figure 16 presents the influence of viscous dissipation parameter on temperature profile of the model. The graph is plotted $\theta$ versus $\eta$ denoting dimensionless temperature along the vertical axis and dimensionless distance along the horizontal axis respectively. From the simulation study it can be observed that as viscous dissipation parameter increases temperature profile of the model decreases. Eckert number is the ratio of stretching velocity at the plate to the specific enthalpy difference between the plate and micropolar fluid. Viscous dissipation parameter describes the measure of frictional heat which has retarding effect on the flow of micropolar fluid. Physiologically, this can be expressed as blood flow in the vessel there is decrement of thermal radiation due to frictional heat transfer of the fluid. Consequently, increment of viscous dissipation results in decrement of temperature within the fluid.

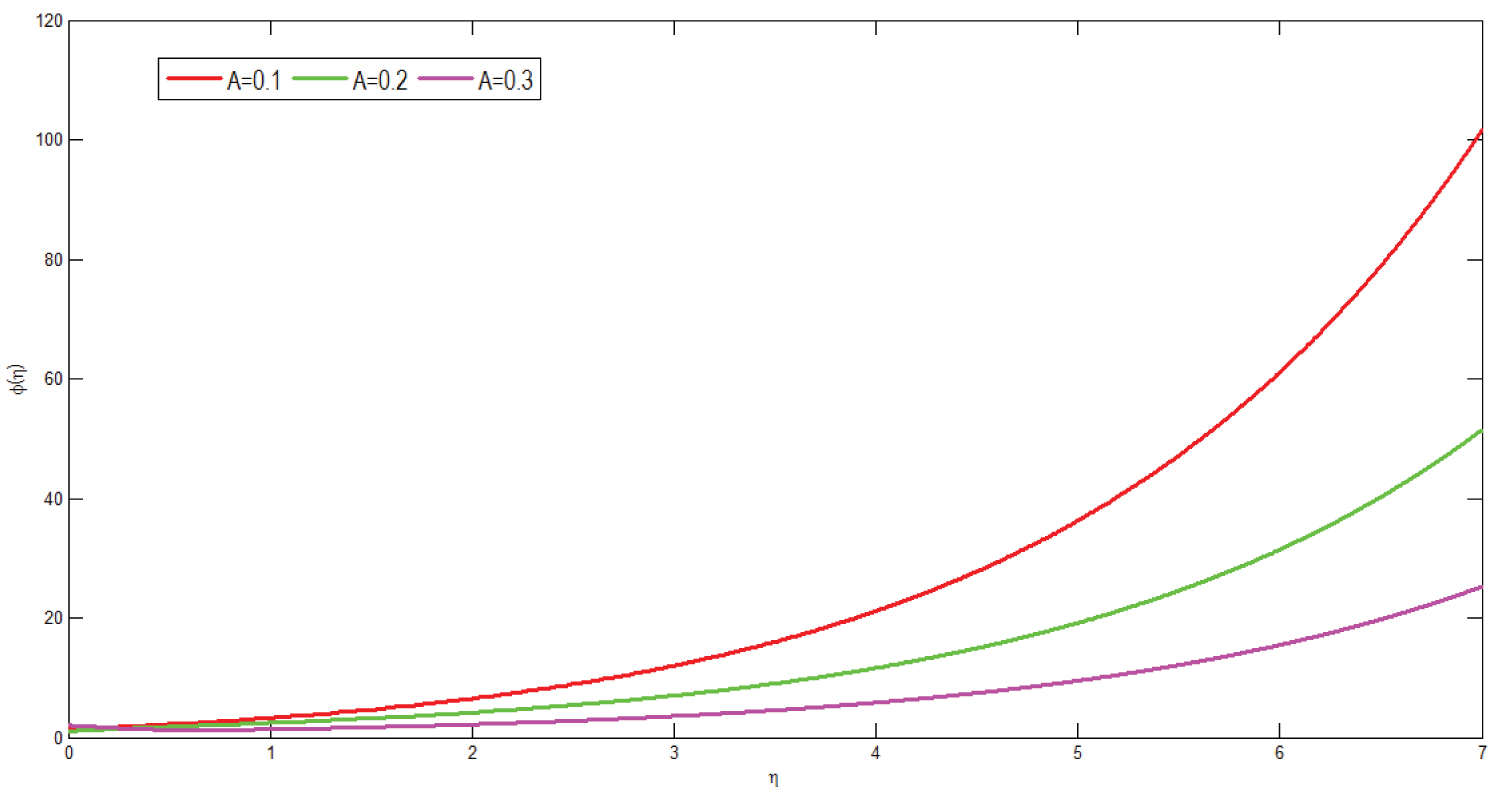
Figure 17 shows the effect of unsteadiness parameter on concentration profile of the model. The graph is drawn $\varphi$ versus $\eta$ representing dimensionless concentration along the vertical axis and dimensionless distance along the horizontal axis respectively. From the Figure it can be concluded that an increment in unsteadiness parameter results in decrement of concentration.

Figure 18 shows the effect of chemical reaction on concentration profile of the model. The graph is plotted $\varphi$ versus $\eta$ for different values of dimensionless concentration against dimensionless distance. From the simulation study it can be concluded that as chemical reaction parameter increases the concentration of micropolar fluid decreases. Biologically, this shows that diffusion rates of micropolar fluid are changed due to the influence of destructive chemical reaction. Chemical reaction is said to be destructive if heat is absorbed. In this case chemical reaction is an endothermic reaction. Consequently, an increment of chemical reaction parameter results in decrement of concentration.

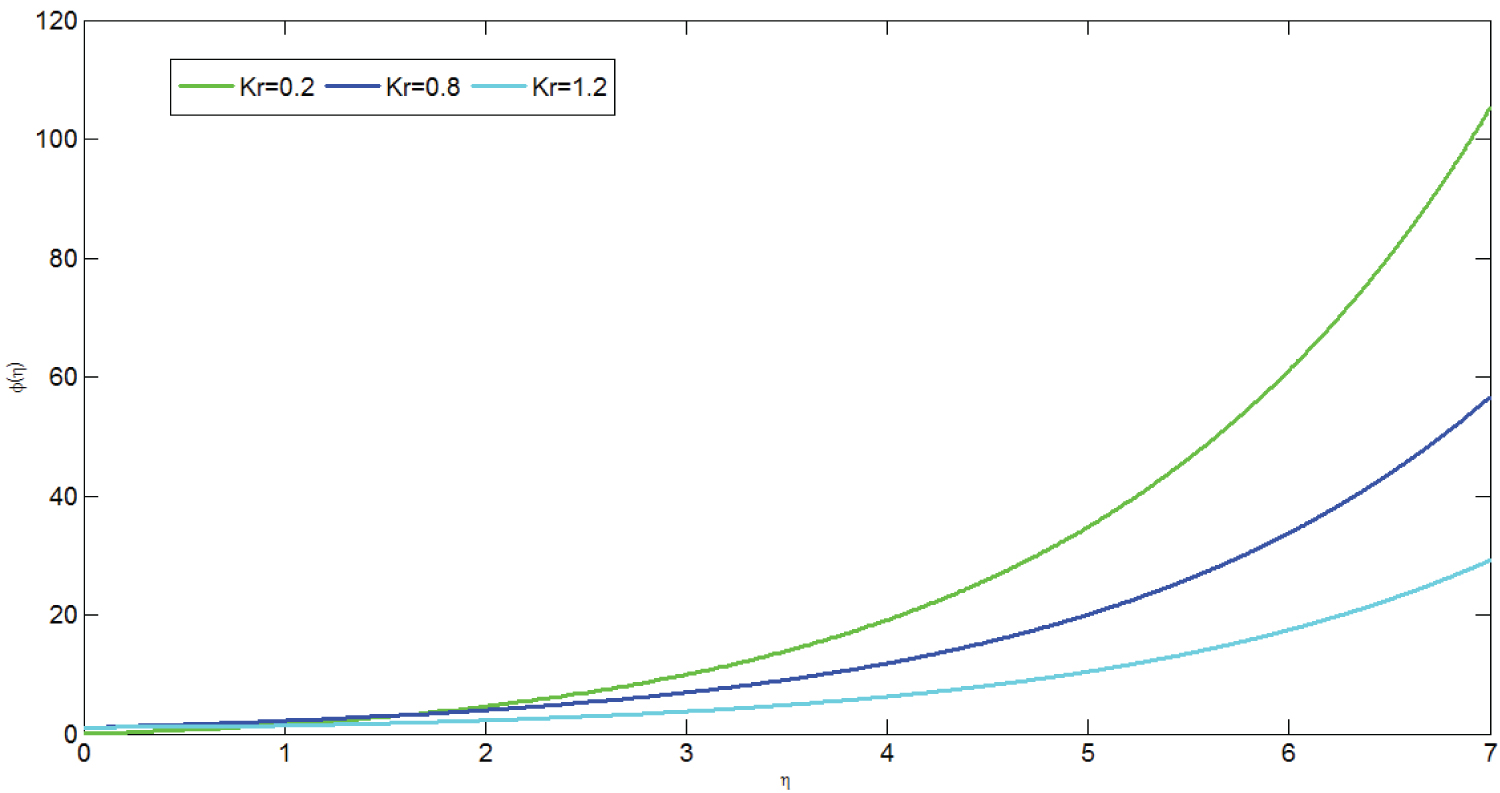
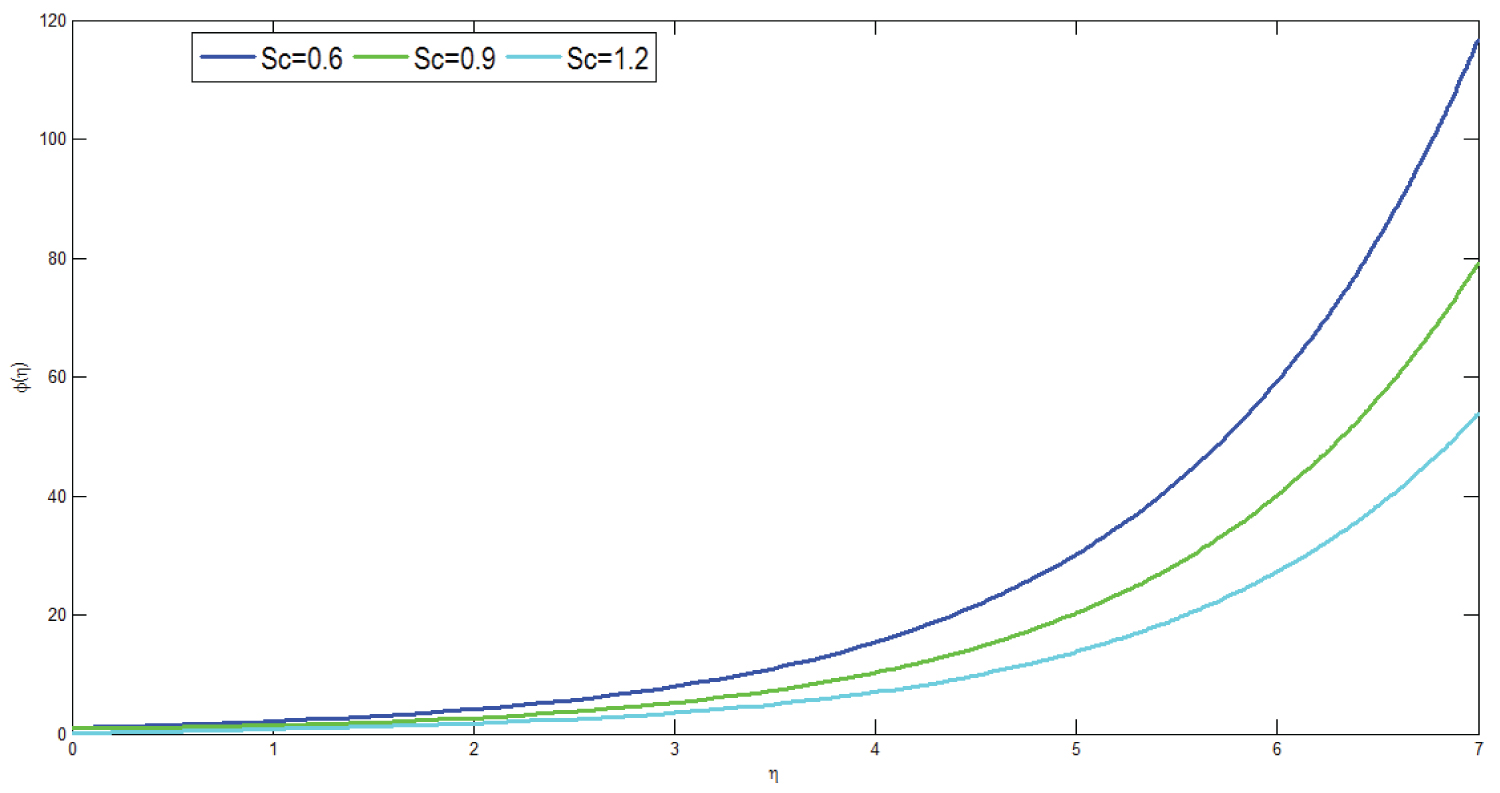
Figure 19 depicts the concentration profile of the model for different values of Schmidt number. The graph is plotted $\varphi$ versus $\eta$ representing respectively dimensionless concentration and dimensionless distance respectively. From the graph it can be concluded that as Schmidt number increases concentration of micropolar fluid decreases. Physiologically, this decrement causes concentration buoyancy effects to decrease the velocity of fluid flow which results in decreasing concentration of micropolar fluid.

Finally, in order to check the accuracy of the present results comparison is made with literature reviews published papers previously. As it is shown in Table 1 the numerical values of local Nusselt number $-\theta \text{'}\left(0\right)$ in this paper for different values of unsteadiness parameter and thermal buoyancy parameter are in good agreement with the result published in Abdul Aziz et al [15]. Hence the results are accurate to analyze this flow.

The effects of unsteadiness parameter A thermal buoyancy parameter $\tau ,$ micropolar parameter $k_c,$ thermal radiation parameter R and Schmidt number Sc on local skin coefficient $f\text{'}\text{'}\left(0\right)$, local wall couple stress $g\text{'}\left(0\right)$, local Nusselt number $-\theta \text{'}\left(0\right)$ and local Sherwood number $-\varphi \text{'}\left(0\right)$ are presented in [Table 2]. From [Table 2] it can be concluded that local skin friction coefficient with an increase value of both unsteadiness parameter and micropolar parameter increases in the case of assisting flow $\left(\tau >0\right)$.

Moreover, the effect of unsteadiness parameter and micropolar parameter on local couple stress is shown in Table 2. From this it can be deduced that an increment of unsteadiness parameter and micropolar parameter results in an increment of the local couple stress.

Increasing value of unsteadiness and thermal radiation parameter results in increasing of the rate of heat transfer. Finally, the effect of Schmidt number and unsteadiness parameter on local Sherwood number has been shown. From Table 2 it can be concluded that an increment in unsteadiness parameter and Schmidt number results in decrement of Sherwood number.

Theoretical Analysis and Experimental Discussions of Micropolar Fluid

Many scholars have conducted experiments on flow characteristics of blood flow through artery by considering blood as Newtonian (Young (1968); Morgan and Young (1974); Lee and Fung (1970)). The Newtonian behavior can be applied in larger arteries, but blood can behave as non-Newtonian in small arteries (Sapna and Shah (2011)). Micropolar fluid has non-Newtonian characteristics. Ariman (1974) studied blood flow in a rigid circular tube and concluded micropolar fluid model is better model because it possesses microrotation blood suspension.

Conclusion

In this paper numerical and theoretical analysis of thermal radiation, chemical reaction and viscous dissipation effects on MHD mixed convection flow of a micropolar fluid with stretching surface in the presence of heat generation/absorption has been studied. The nonlinear partial differential equations are converted to ordinary differential equations using similarity transformations which are solved numerically.

From the simulation study the following important results are obtained:

I. An increment of micropolar parameter, Hartmann number, unsteadiness parameter, thermal and concentration buoyancy parameter results in decrement of velocity flow of micropolar fluid.

II. Microrotation of micropolar fluid decreases with an increment of micropolar parameter, unsteadiness parameter, micro inertial density parameter and spin gradient viscosity parameter.

III. Temperature profile of micropolar fluid decreases with an increment of thermal radiation parameter, Prandtl number, micropolar parameter, unsteadiness parameter, heat absorption and viscous dissipation parameter.

IV. Concentration of micropolar fluid decreases as unsteadiness parameter, Schmidt number and chemical reaction parameter increases.

V. The coefficient of skin friction enhanced with an increase value of both unsteadiness parameter and micropolar parameter.

VI. Increasing values of unsteadiness parameter and micropolar parameter results in an increment of the local couple stress.

VII. An increment values of unsteadiness parameter and thermal radiation parameter results in an increment of the rate of heat transfer.

VIII. As the values of Schmidt number and unsteadiness parameter increases Sherwood number decreases.

Application of the Model

This can be applied to model micropolar fluid for blood flow

1. To treat abnormal thickness of arterial wall.

2. To study blood flow characteristics of cardiovascular, cerebrum and pulmonary systems.

3. To model theory and simulation study of micropolar fluid through an artery in both stenosis and post stenosis dilatation.

Nomenclature

u : Velocity of the fluid flow along x axis $[m{s}^{-1}]$

v : Transverse velocity of fluid flow $[m{s}^{-1}]$

$\mu$ : Dynamic viscosity $\left[Kg{m}^{-1}{s}^{-1}\right]$

$\rho$ : Fluid density $\left[Kg{m}^{-3}\right]$

k : Vortex viscosity of the fluid

$\beta$ : Volumetric coefficient of thermal expansion $\left[K^{-1}\right]$

${\beta }_c$ : Volumetric coefficient of concentration expansion $\left[K^{-1}\right]$

v : Kinematic viscosity $\left[m^2{s}^{-1}\right]$

j : Micro inertia density $\left[m^2\right]$

$N$ : Spin gradient viscosity $\left[Ns\right]$

N : Component of microrotation $\left[rad{s}^{-1}\right]$

g : Gravitational acceleration $\left[m{s}^{-2}\right]$

$q_r$ : Radiative heat flux

A : Unsteadiness parameter

Sc : Schimdt number

M : Hartmann number

Pr : Prandtl number

R : Radiative parameter

$\eta$ : Dimensionless distance

$U_W$ : Streching velocity along x axis

$C_W$ : Concentration along the x axis

$T_W$ : Wall temperature along the x axis

$T_{\infty }$ : Ambient temperature of the medium

$C_{{}_{\infty }}$ : Ambient concentration of the solute

$C_P$ : Specific heat capacity at constant pressure $\left[JK{g}^{-1}{K}^{-1}\right]$

$\alpha$ : Thermal diffusivity

$D$ : Molecular diffusivity $\left[m^2{s}^{-1}\right]$

$\sigma$ : Electrical conductivity $\left[{\left(ohm\right)}^{-1}\right]$

$k_r$ : Chemical reaction parameter

$k_c$ : Micropolar parameter

$\tau$ : Thermal buoyancy parameter

$\chi$ : Concentration buoyancy parameter

$\lambda$ : Spin gradient viscosity parameter

$\zeta$ : Microinertial density parameter

$Ec$ : Eckert number

$x,y$ : Axial and perpendicular coordinates [m].

Data Availability

There are no data available for this research.

Conflicts of Interest

The author declares that there are no conflicts of interest.

References

1. Eringen AC (1964) Simple Micro Fluids. Int J Engg Sci 2: 205-217.
2. Ariman T, Turk MA, Sylvester N (1974) Application of micro continuum fluid mechanics. Int J Engg Sci 12: 273-293.
3. Philip D, Chandra P (1995) Peristaltic transport of a simple micro fluid. Proc Nat Acad Sci India 65: 63-74.
4. Giraja Devi R, Devanatan R (1975) Peristaltic motion of micropolar fluid. Proc Indian Acad Sci 81: 149-163.
5. Hiremath PS (1983) Flow of micro fluid through a channel with injection Acta Mechanica 46: 271-279.
6. Gorla RSR, Takhar HS, Slaouti A (1998) Magnetohydrodynamics free convection boundary layer flow of a thermomicropolar fluid over a vertical plate. Int J Engg Sci 36: 315-327.
7. Bhargava R, Kumar L, Takhar HS (2003) Numerical solution of free convection MHD micropolar fluid flow between two parallel porous vertical plates. Int J Eng Sci 41: 123-136.
8. Zigta B, Koya P (2017) The effect of MHD on free convection with periodic temperature and concentration in the presence of thermal radiation and chemical reaction. International Journal of Applied Mechanics and Engineering 22: 1059-1073.
9. Zigta B (2018) Effect of thermal radiation, chemical reaction and viscous dissipation on MHD flow. International Journal of Applied Mechanics and Engineering 23: 787-801.
10. Zigta B (2019) Thermal radiation, chemical reaction, viscous and joule dissipation effects on MHD flow embedded in a porous medium. International Journal of Applied Mechanics and Engineering 24: 725-737.
11. Zigta B (2020) Mixed convection on MHD flow with thermal radiation, chemical reaction and viscous dissipation embedded in a porous medium. International Journal of Applied Mechanics and Engineering 25: 219-235.
12. Zigta B (2020) Effect of thermal radiation and chemical reaction on mhd flow of blood in stretching permeable vessel, international journal of applied mechanics and engineering 25: 198.
13. Sing PJ, Roy S, Ravindran R (2009) Unsteady mixed convection flow over a vertical wedge. J. Heat and mass transf 52: 415-421.
14. Zueco J, Eguia P, Abd El-Aziz M, et al. (2009) Unsteady MHD free convection of a micropolar fluid between two parallel porous vertical walls with convection from the ambient. International communications in Heat and Mass Transfer 36: 203-209.
15. Abd El-Aziz M (2013) Mixed convection flow of a micropolar fluid from an unsteady stretching surface with viscous dissipation. Journal of the Egyptian Mathematical Society 21: 385-394.
16. Hussain M, Ashraf M, Nadeem S, et al. (2013) Radiation effects on the thermal boundary layer flow of micropolar fluid towards a permeable stretching sheet. Journal of the Franklin Institute 350: 194-210.
17. Oahimire JI, Olajuwon B (2014) Effect of Hall current and thermal radiation on heat and mass transfer of a chemically reacting MHD flow of a micropolar fluid of a porous medium. Journal of King Saud University Engineering Sciences 26: 112-121.
18. Das UN, Deka RK, Soundalgekar VM (1995) Effects of mass transfer on the flow of past an impulsively started infinite vertical plate with constant heat flux and chemical reaction. Forschung im Ingenieurwesen 60: 284-287.
19. Crane LJ (1970) Flow past a stretching plate. Zeitschrif Fur Angewandte Mathematic and Physic 21: 645-647.
20. Bhargava R, Kumar L, Takhar HS (2003) Finite element solution of mixed convection micropolar flow driven by a porous stretching sheet. International Journal of Engineering Science 41: 2161-2178.
21. Eldabe NT, Ouaf MEM (2006) Chebyshev finite difference method for heat and mass transfer in a hydromagnetic flow of a micropolar fluid past a stretching surface with Ohmic heating and viscous dissipation. Applied Mathematics and Computation 177: 561-571.
22. Pal D, Mandal G, Vajravelu K (2013) MHD convection dissipation heat transfer over a nonlinear stretching and shrinking sheets in nanofluids with thermal radiation. International Journal of Heat and Mass Transfer 65: 481-490.
23. Mahmoud MAA, Waheed SE (2012) MHD flow and heat transfer of a micropolar fluid over a stretching surface with heat generation absorption and slip velocity. Journal of the Egyptian Mathematical Society 20: 20-27.
24. Grzegorz L (1999) Micropolar fluids Theory and applications. Birkhauser Boston 20-23.
25. Hsiao K-L (2017) To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy 130: 486-499.
26. Hsiao K-L (2017) Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature International Journal of Heat and Mass Transfer 112: 983-990.
27. Hsiao K-H (2017) Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Applied thermal Engineering 112: 1281-1288.
28. Singh K, Kumar M (2016) Effects of thermal radiation on mixed convection flow of a micropolar fluid from an unsteady stretching surface with viscous dissipation and heat generation/ absorption. International Journal of Chemical Engineering