Journal of Fluid Dynamics

The Effect of Nanoparticles on MHD Blood Flow in Stretching Arterial Porous Vessel with the Influence of Thermal Radiation, Chemical Reaction and Heat Generation/Absorption

Abstract

Numerical and theoretical analysis of the effect of nanoparticles on MHD blood flow in stretching arterial porous vessel with the influence of thermal radiation, chemical reaction and heat generation/absorption has been examined. The governing non-linear partial differential equations of momentum, energy and nanoparticles concentration are converted into ordinary differential equations using similarity transformations which are solved numerically. The dimensionless governing equations are solved using Runge-Kutta-Fehlberg fourth-fifth order along with shooting method. The effect of physical parameters viz., Hartmann number, unsteadiness parameter, permeability parameter, Brownian motion parameter, thermophoresis parameter, thermal radiation parameter, heat source parameter, chemical reaction parameter and Lewis number on flow variables viz., velocity of nanofluid, temperature and nanoparticles concentration has been analyzed and discussed graphically. From the simulation study the following important results are obtained: velocity of nanofluid flow increases with an increment of unsteadiness and permeability parameter; velocity of nanofluid decreases with an increment of Hartmann number; temperature profile of the model problem increases as Brownian motion parameter, thermophoresis parameter, thermal radiation parameter and heat source parameter increases. An increment in Lewis number and chemical reaction parameter results in decrement of nanoparticles concentration of the nanofluid. As the value of thermophoresis parameter increases nanoparticles concentration of the nanofluid increases.

Keywords

Nanoparticles, Brownian motion parameter, Thermophoresis parameter, Thermal radiation, Chemical reaction

Introduction

Blood is considered as a multi component non-Newtonian fluid which is composed of red blood cells, white blood cells, platelets and plasma. Pulsatile blood flow in cardiovascular system employing the Navier-Stokes equation and detected an increase in the wall shear stress when the porosity of the medium has been increased was modeled in [1]. Mathematical model for pulsatile blood flow subjected to externally impose periodic body acceleration by considering blood as third grade fluid has been created in [2]. The pathological situation of blood vessel was modeled and numerical solution obtained by using finite difference in [3].

Nanotechnology becomes significant field of study and has very wide applications in biology, chemistry, physics and engineering. Nanofluid is a new class of nanotechnology based on heat transfer fluids that enhances thermal properties compared with that of classical fluid particles. Nanofluid is the interaction of nanoparticles in a fluid. Nanoparticles used in nanofluids are consisted of base fluids such as water, ethylene, glycol and oil which are conductive fluids; moreover, nanoparticles are made up of metals and nonmetals such as copper, mercury, oxides, carbides, nitrides, carbon nanotubes and graphite. Nanofluid has wide applications in convective heat transfer. Model of nanofluid flow based on the Brownian motion and thermophoresis was formulated in [4]. The boundary layer flow produced in a nanofluid due to a linearly stretching by using a convective heating boundary condition studied in [5]. Mixed convection flow of a power-law nanofluid over a non-linearly stretching surface examined in [6].

Recently, Magneto hydrodynamics has received more attention due to its applications viz., petroleum industry, space dynamics, plasma physics, nuclear science and engineering. The magneto-nanofluid is the combined effect of fluid flow and heat transfer influenced by external magnetic field. Many researchers have been studied the effect of magnetic field on nanofluid with different geometries. The influence of MHD and viscous dissipation past a non-linear stretching sheet studied in [7]. Numerical solution of MHD nanofluid across stretching sheet with thermal radiation and second order slip conditions have been studied in [8]. Heat generation/absorption and thermophoresis effects on MHD flow past an oscillatory stretching sheet presented in [9]. The joint effect of magnetic field and thermal radiation for nanofluid flow and heat transfer amidst two horizontal parallel plates by considering two component models have been studied in [10]. The double effect of magnetic field and thermal radiation past a vertical stretching sheet for 2D water based nanofluid flow has been examined in [11].

In chemical engineering there is chemical reaction between foreign mass and the fluid. This process takes place in industrial application viz., food processing, polymer production and manufacturing of ceramics. Chemical reaction, heat generation/absorption effects on MHD boundary layer flow over a permeable stretching surface have been investigated in [12]. Unsteady MHD flow and heat transfer of nanofluid over a permeable shrinking sheet with thermal radiation and chemical reaction studied in [13]. The effect of MHD on free convection oscillatory Couette flow when the temperature and concentration oscillate with time in the presence of the thermal radiation and chemical reaction has been studied in [14]. The effect of thermal radiation, chemical reaction and viscous dissipation on MHD flow has been studied in [15]. Thermal radiation, chemical reaction, viscous and Joule dissipation effects on MHD flow embedded in a porous medium investigated in [16]. Mixed convection on MHD flow with thermal radiation, chemical reaction and viscous dissipation embedded in a porous medium examined in [17]. Effect of thermal radiation and chemical reaction on MHD flow of blood in stretching permeable vessel studied in [18].

Chemical reaction effect on MHD boundary layer flow of two phase nanofluid model over an exponentially stretching with a heat generation studied in [19]. In this study the effect of nanoparticles with the influence of time dependent magnetic field and time dependent velocity has not been considered. This omission encourages studying the effect of nanoparticles on MHD blood flow in stretching arterial porous vessel with the influence of thermal radiation, chemical reaction and heat generation/absorption.

The main objective of this study focuses on the effect of nanoparticles on MHD blood flow in stretching arterial porous vessel with the influence of thermal radiation, chemical reaction and heat generation/absorption with no velocity, thermal and concentration slip in the arterial porous vessel.

Mathematical Analysis of Nanofluid Model

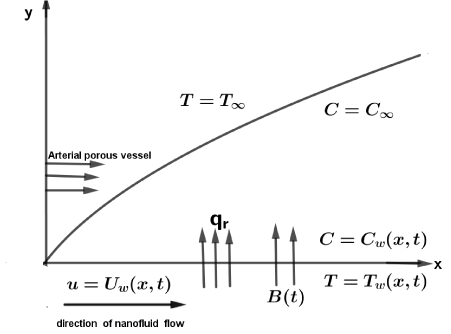
Consider two dimensional unsteady, incompressible, mixed convection, viscous, electrically conducting nanofluid and permeable stretching arterial vessel with the influence of time dependent magnetic field, thermal radiation, chemical reaction and heat generation/absorption. The x axis is taken along the stretching arterial porous vessel in the direction of motion and the y axis is normal to it as shown in Figure 1. The nanofluid is moving due to permeable stretching arterial vessel caused by time dependent magnetic field applied in transverse direction of the flow. Furthermore, the fluid is considered to be a gray in color, has radiation absorbing emitting nature but non-scattering medium in the optically thick limit. Rossel and approximation is used to describe the radiative heat flux applied perpendicular to the stretching arterial porous vessel. The ambient values of temperature and concentration are given by T∞ and C∞ respectively.

Consider MHD nanofluid flow in the arterial porous vessel is influenced by time dependent magnetic field which is applied in transverse direction of nanofluid flow. The arterial porous vessel is assumed to be stretched with velocity $Uw\left(x,t\right);Tw(x,t)$ and is arterial surface temperature and nanoparticles concentration of the blood are taken along the x axis respectively; and time dependent chemical reaction parameter $k_r(t)$ takes the following form

$$\begin{array}{l}{U}_w\left(x,t\right)=\frac{ax}{1-ct},T_w\left(x,t\right)=T_{\infty }+\frac{ax}{{\left(1-ct\right)}_{}^2},C_w\left(x,t\right)=C_{\infty }+\frac{bx}{{\left(1-ct\right)}_{}^2},\\ k_r\left(t\right)=\frac{k_o}{D_B{\left(1-ct\right)}_{}^{}}\text{ (1)}\end{array}$$

Where a,b,c and $k_o$ are the constants such that $a>0,b\ge 0,c\ge 0$ and $t<c_{}^{-1}$. Let us choose $B(t)=\frac{B_o}{\sqrt{\left(1-ct\right)}},B_o$ denotes the magnetic field strength at t = 0 and $K_r\left(t\right)$ is chemical reaction rate of the fluid.

The expressions, and are valid if $ct<1$ unless $c=0$ . Furthermore, the velocity describes the stretching arterial porous vessel is stretched in the positive direction and the rate of stretching increases with time. The arterial surface temperature $T_w\left(x,t\right)$ of the stretching arterial porous vessel describes the situation in which the temperature increases if $b>0$ and decreases if $b<0.$ The nanoparticles concentration of blood describes the situation in which it increases if $b>0$ and decreases if $b<0$.

To derive the governing equations the following model assumptions are made

1. MHD nanofluid is an electrically conducting fluid. Blood can be considered as MHD nanofluid.

2. Time dependent magnetic field is applied in the direction transverse to the flow of nanofluid.

3. The magnetic Reynolds numbers are small so that the induced magnetic field of the fluid is negligible.

4. Time dependent permeability of arterial porous vessel is considered.

5. The external electric field is supposed to be zero.

6. The electric field due to polarization of charges is negligible.

7. Velocity, thermal and concentration slip are negligible.

8. Thermal radiation, chemical reaction and heat absorption/generation are taken in to consideration.

Based on model assumptions, the governing equations of conservation of mass, momentum, energy and nanoparticles concentration of equation of MHD nanofluid can be expressed as follows:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\left(2\right)$$

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{u}{{\rho }_f}\frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma B^2\left(t\right)u}{{\rho }_f}-\frac{u}{k_1\left(t\right){\rho }_f}u\left(3\right)$$

$$\begin{array}{l}\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}-\Gamma \left[D_B\left(\frac{\partial c}{\partial y}\right)\left(\frac{\partial T}{\partial y}\right)+\left(\frac{D_T}{T_{\infty }}\right){\left(\frac{\partial T}{\partial y}\right)}_{}^2\right]-\\ \frac{1}{{\left(\rho C_p\right)}_f^{}}\frac{\partial q_r}{\partial y}+\left(\frac{Q_o}{{\left(\rho C_p\right)}_f^{}}\right)\text{ (4)}\end{array}$$

$$\frac{\partial c}{\partial t}+u\frac{\partial c}{\partial x}+v\frac{\partial c}{\partial y}=D_B\frac{{\partial }_{}^{2}c}{\partial y_{}^2}+\left(\frac{D_T}{T_{\infty }}\right){\left(\frac{\partial T}{\partial y}\right)}_{}^2-k_r\left(C-C_{\infty }\right)\left(5\right)$$

Here in Eqs. (2)-(5), u and v denotes the velocity components along x and y axis respectively. Thermal diffusivity of the nanofluid is represented as and the ratio of heat capacity of nanoparticles to the fluid is denoted by. Density of the fluid is denoted by; density of the nanoparticles is represented as ; denotes electric conductivity of the fluid; is the specific heat capacity at constant pressure; represents time dependent permeability of arterial porous vessel ; denotes effective heat capacity of the nanoparticles; represents effective heat capacity of the fluid; represents Brownian diffusion coefficient; denotes thermophoresis diffusion coefficient; is the volumetric rate of heat generation/absorption within the fluid; is the radiative heat flux; represents time dependent first order chemical reaction rate, destructive chemical reaction; generative chemical reaction and no chemical reaction T and C are temperature and nanoparticles concentration respectively.

$$u=U_w,v=0,T=T_w,C=C_{w}aty=0\text{ (6)}$$

u → 0, T → T_∞, C → C_∞ as y → ∞

It is assumed that the boundary layer is optically thick and the Roseland approximation for radiation is valid [Cortel.R, 2008]. Hence the radiative heat flux for an optically thick boundary layer [Brewster, 1992] is given by

$$q_r=\left(\frac{-4{\sigma }_{}^{*}}{3k_s}\right)\left(\frac{\partial T_{}^4}{\partial y}\right)\text{ (8)}$$

In (8), the parameters ${\sigma }_{}^{*}$ and $k_s$ represent the Stefan Boltzmann constant and the Roseland mean absorption coefficient, respectively.

Taking the nanoparticles flow temperature as very small, in Eq. (8) can be expanded as a linear function of ,

$$T_{}^4\cong T_{\infty }^4+4\left(T-T_{\infty }\right)T_{\infty }^3+6{\left(T-T_{\infty }\right)}_{}^2{T}_{\infty }^2+\mathrm{...}\text{ (9)}$$

After neglecting higher order terms in Eq. (9), $T_{}^4$ can be expanded as

$$T_{}^4\cong 4T_{\infty }^{3}T-3T_{\infty }^4\text{ (10)}$$

Using Eq. (10), the radiative heat flux can be expressed as

$$\partial q_r/\partial y=\left(-16T_{\infty }^3{\sigma }_{}^{*}/3k_s\right)\left({\partial }_{}^{2}T/\partial y_{}^2\right)\left(11\right)$$

Using Eq. (11) in Eq. (4) the following equation is obtained

$$\begin{array}{l}\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}-\Gamma \left[D_B\left(\frac{\partial c}{\partial y}\right)\left(\frac{\partial T}{\partial y}\right)+\left(\frac{D_T}{T_{\infty }}\right){\left(\frac{\partial T}{\partial y}\right)}_{}^2\right]+\\ \frac{1}{{\left(\rho C_p\right)}_f}\left(\frac{16T_{\infty }^3{\sigma }_{}^{*}}{{}_{}3k_s}\right)\left(\frac{{\partial }^{2}T}{\partial y^2}\right)+\left(\frac{Q_o}{{\left(\rho C_p\right)}_f}\right)(T-T_{\infty })\left(12\right)\end{array}$$

Non-Dimensionalization of the Model

In order to find similarity solution of the problem the following non dimensional variables are introduced [Ludlow, Clarkson and Bassom, 2000]

$$\eta =\sqrt{\frac{a}{v\left(1-ct\right)}}y,\psi =\sqrt{\frac{va}{1-ct}}xf\left(\eta \right),T=T_{\infty }+\frac{bx}{1-ct}\theta \left(\eta \right),\text{ (13)}$$

The continuity equation (2) satisfies the stream function defined by

$$u=\frac{\partial \Psi }{\partial y}=U_{w}f\text{'}\left(\eta \right),\text{ (14)}$$

$$v=-\frac{\partial \Psi }{\partial x}=-\sqrt{\frac{va}{1-ct}}f\left(\eta \right).\text{ (15)}$$

Where $\psi \left(x,y,t\right)$ the stream function is defined by which satisfies continuity equation (2).

Substitution of Eq. (13) into equations (2)-(5), the following similarity equations are obtained:

$$f\text{'}\text{'}\text{'}+ff\text{'}\text{'}-f_{}^{\text{'}2}-A(f\text{'}+\frac{\eta }{2}f\text{'}\text{'})-M_{}^{2}f\text{'}-\frac{1}{k_3^{}}f\text{'}=0\left(16\right)$$

$$\left(\frac{1+R}{pr}\right)\theta \text{'}\text{'}-\Gamma \left[Nb\varphi \text{'}\theta \text{'}+Nt{\theta }_{}^{\text{'}2}\right]+\omega \theta -A\left[2\theta +\frac{\eta }{2}{\theta }_{}^{\text{'}}\right]-f\text{'}\theta +f\theta \text{'}=0\left(17\right)$$

$$\theta \text{'}\text{'}+Le(Nt{\theta }_{}^{\text{'}2}-A\left[2\varphi +\frac{\eta }{2}{\varphi }_{}^{\text{'}}\right]-\left[f\text{'}\varphi -f{\varphi }_{}^{\text{'}}\right])-k_r\varphi =0\left(18\right)$$

In equation (16)-(18), A is unsteadiness parameter; Nb is Brownian motion parameter; is thermophoresis parameter; is Lewis number; M is the Hartmann number; R is the radiation parameter; k₃ is permeability parameter; denotes the ratio of heat capacity of nanoparticles to the fluid; Pr is the Prandtl number; is chemical reaction parameter and ω are heat generation/ absorption represented respectively by

$$A=c/a;Nb=\left(\frac{D_B}{v}\right)(C-C_{\infty });Nt=\left(\frac{D_T}{T_{\infty }v}\right)(T-T_{\infty });Le=v/D_{B}M=B_0\sqrt{\sigma /{\rho }_{f}a;}$$

$\omega =\frac{Q_o}{k}$ and

The corresponding boundary conditions (6)-(7) reduces to

$f\left(\eta \right)=0,f\text{'}\left(\eta \right)=1,\theta \left(\eta \right)=1$ and $\varphi \left(\eta \right)=1$ at $\eta =0,$      (19)

$f\text{'}\left(\eta \right)=0,\theta \left(\eta \right)=0$ and $\varphi \left(\eta \right)=0$ as      (20)

Numerical Solution to the Problem

The set of coupled non linear ordinary differential equations (16)-(18) with boundary conditions (19)-(20) are solved numerically using Runge-Kutta-Fehlberg fourth-fifth order along with shooting method. The values of boundary conditions at and are satisfied. In order to choose the appropriate value of we start with some initial guess value and solve the boundary value problem to obtain and at. Using computer language MATLAB code for different values of and step sizes it can be observed that there is no change in velocity, temperature and concentration for values of Therefore in the present study the value ofis selected to vary from 2 to 10 depending on the physical parameters and step size are taken. The coupled non linear ordinary differential equations are third order in and second order in and which have been converted in to seven simultaneous equations. There are four initial conditions at $\eta =0$ and three boundary conditions To find the solution of the problem there are three more initial conditions at, the values of $f",\theta \text{'}$ and $\varphi \text{'}$ these conditions are determined by shooting technique. Then the solutions of the problem are solved using Runge-Kutta-Fehlberg fourth-fifth order.

First convert higher order non linear differential equations to system of first order ordinary differential by using

$$y_1=f,y_2=f\text{'},y_3=f",y_4=\theta ,y_5=\theta \text{'},y_6=\varphi ,y_7=\varphi \text{'}$$

$$y_2^{\text{'}}=y_2$$

$$y_2^{\text{'}}=y_3$$

$$y_3^{\text{'}}=y_2{}_{}^2-y_1{y}_3+A\left(y_2+\eta /2y_3\right)+y_2(M_{}^2+1/k_3)$$

$$y_4^{\text{'}}=y_5$$

$$y_5^{\text{'}}=\mathrm{Pr}/\left(1+R\right)\left\{\Gamma (Nb{y}_7{y}_5+Nt{y}_5^2)-\omega y_4+A(2y_4+\eta /2y_5)+y_2{y}_4-y_1{y}_5\right\}$$

$$y_6^{\text{'}}=y_7$$

$$y_7^{\text{'}}=Le\left[-Nt{y}_5^2+A(\eta /2y_7+2y_6)+(y_2{y}_6-y_1{y}_7)\right]+k_r^{\text{'}}{y}_6$$

With corresponding boundary conditions

$$y_1(\eta )=0,y_2(\eta )=1,y_4(\eta )=1,y_6(\eta )=1,y_3(\eta )=m$$

$$y_5(\eta )=n,y_7(\eta )=l$$

Where $m,n,l$ and $w$ are unknown to be computed using shooting technique to solve numerically.

Simulation Study of the Model

In this section the effect of nanoparticles on MHD blood flow in permeable stretching arterial vessel with the influence of time dependent magnetic field, thermal radiation, chemical reaction and heat generation/ absorption has been studied. The effect of physical parameters viz., Hartmann number, unsteadiness parameter, permeability parameter, Brownian motion parameter, thermophoresis parameter, thermal radiation parameter, heat source parameter, chemical reaction parameter and Lewis number on flow variables viz., velocity, temperature and nanoparticles concentration has been analyzed and discussed graphically.

The governing nonlinear partial differential equations are converted in to simulataneous set of ordinary differential equations using similarity transformations which can be solved numerically using Runge-Kutta-Fehlberg fourth-fifth order along with shooting technique.

Graphical represntations of velocity profile for different values of Hartmann number, unsteadiness parameter and permeability parameters; Temperature profile for different values of Brownian motion parameter, thermophoresis parameter, thermal radiation parameter and heat source parameter. Furthermore, concentration profile for different values of thermophoresis parameter, chemical reaction parameter and Lewis number has been presented.

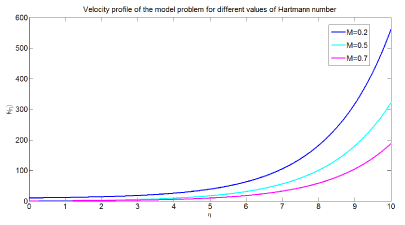
Figure 2 describes the effect of Hartmann number on velocity profile of the model. The graph is plotted versus for different values of dimensionless velocity against dimensionless distance respectively. From the figure it can be observed that as the values of Hartmann number increases the velocity of nanofluid decreases this occurs due to the Lorentz force which tends to resist the fluid flow and hence reduce the velocity of nanofluid flow.

Blood containing nanoparticles are considered as non-Newtonian nanofluid. Physiologically, this can be expressed velocity of nanoparticles in the blood vessel decreases due to red blood cells which contain high concentration of hemoglobin molecules. This results in an increment of concentration of red blood cells hence internal blood viscosity increases thus velocity of blood flow decreases. This is due to attribution of magnetic field which causes red blood cells to flow in the direction parallel to the magnetic field.

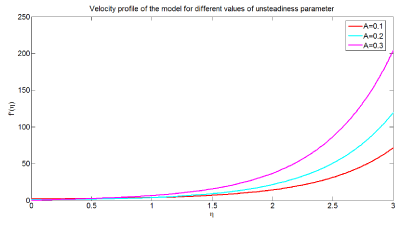
Figure 3 depicts the effect of unsteadiness parameter on velocity profile of the model. The graph is plotted versus with dimensionless velocity in the vertical axis and dimensionless distance in horizontal axis respectively. For particular value of unsteadiness parameter the value of nanofluid velocity starts from zero and increases as the value of dimensionless distance increases. From the simulation results it can be deduced that as unsteadiness parameter increases the velocity flow of nanofluid increases this causes increment of momentum boundary layer. Physiologically, this can be interpreted as the flow of nanofluid with slip or no slip boundary layer of arterial vessel increases unsteadiness parameter which results in an increment of velocity of the nanofluid.

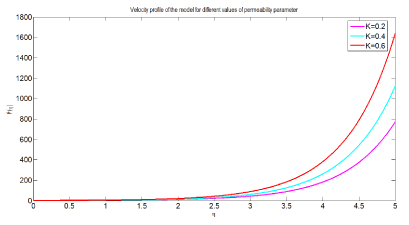
Figure 4 describes the effect of permeability parameter on velocity of nanofluid flow. The graph is drawn versus for different values of dimensionless velocity against dimensionless distance. As the values of permeability parameter increases, the velocity profile of nanofluid flow increases. Physiologically, this shows the relationship between velocity of nanoparticles on blood flow and permeability of arterial porous medium parameter i.e., volume of nanoparticles that passes through porous medium dominates the total volume. Hence, the nanoparticles move from one place to another place easily in the vessel.

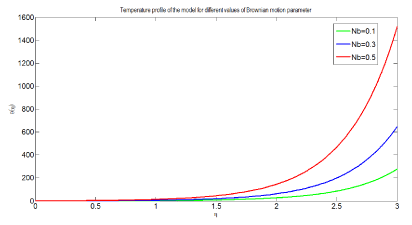
Figure 5 describes the effect of Brownian motion parameter on temperature profile of the model. The graph is plotted versus denoting dimensionless temperature in the vertical axis and dimensionless distance in the horizontal axis respectively. From the graph it can be concluded that as Brownian motion parameter increases temperature profile of the model increases and consequently thermal boundary layer thickness increases. Physiologically, this can be explained as temperature increases in the arterial vessel the Brownian motion of the blood increases. This is due to the fact that Brownian motion parameter is directly proportional to Brownian diffusion coefficient associated with the nanofluid which results in an increment of mass transfer rate in the arterial vessel.

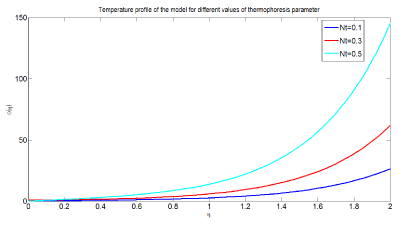
Figure 6 depicts the effect of thermophores is parameter on temperature profile of the model. The graph is plotted versus denoting dimensionless temperature in the vertical axis and dimensionless distance in the horizontal axis respectively. From the simulation study it can be observed that as thermophores is parameter increases temperature profile of the model also increases. Physiologically, this can be interpreted as temperature in the arterial vessel increases this is due to the fact that thermophores is parameter is directly proportional to the heat transfer coefficient associated with the nanofluid.

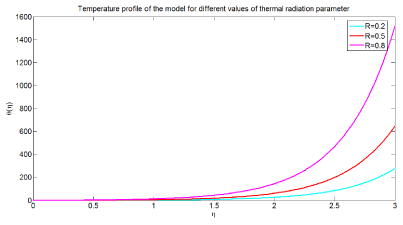
Figure 7 presents temperature profile of the model for different values of thermal radiation parameter. The graph is drawn versus denoting dimensionless temperature in the vertical axis and dimensionless distance in the horizontal axis respectively. From the simulation study it can be observed that an increment in the values of thermal radiation parameter results in an increment of temperature profile of the model. Physiologically, this can be interpreted as thermal radiation increases nanoparticles flow in arterial vessel increases thus temperature of the boundary layer increases. Hence this reduces the effect of thermal buoyancy of body force which increases temperature distribution of the nanofluid. Therefore, an increment in thermal radiation results in an increment of temperature profile of the model.

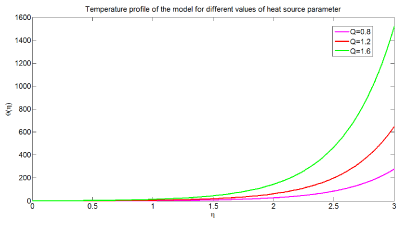
Figure 8 presents the effect of heat source parameter on temperature profile of the model. The graph is drawn versus with dimensionless temperature along the vertical axis and dimensionless distance along the horizontal axis respectively. From the simulation study it can be observed that an increment of heat source parameter results in an increment of temperature profile of the model. Heat source causes to increase thermal boundary layer and the nanofluid becomes hotter. Physiologically, this can be described heat transfer is larger along the arterial vessel this results in an increment of temperature and hence this enhances thermal radiation in the arterial vessel.

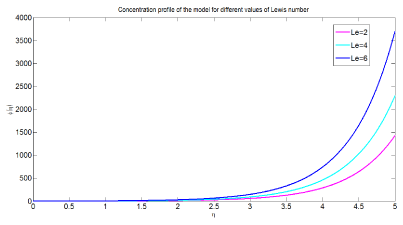
Figure 9 presents the influence of Lewis number on concentration of nanoparticles of the model. The graph is drawn versus for different values of dimensionless concentration on the vertical axis and dimensionless distance on the horizontal axis. From the graphical results it can be observed that as Lewis number increases concentration of nanoparticles decreases and hence concentration boundary layer thickness. Physiologically, this shows an increment of Lewis number results in decrement of Brownian diffusion coefficient. This decrement results in decrement of nanoparticles concentration.

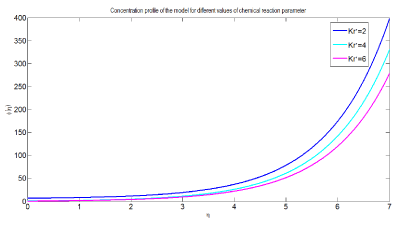
Figure 10 shows concentration of nanoparticles for different values of chemical reaction parameter. The graph is drawn versus for different values of dimensionless concentration on the vertical axis and dimensionless distance on the horizontal axis. From the simulation study it can be concluded that as chemical reaction parameter increases the concentration of nanofluid decreases. Physiologically, this shows that diffusion rates of nanoparticles are changed due to the influence endothermic chemical reaction. Chemical reaction is said to be endothermic if heat is absorbed. Consequently, an increment of chemical reaction parameter results in decrement of concentration.

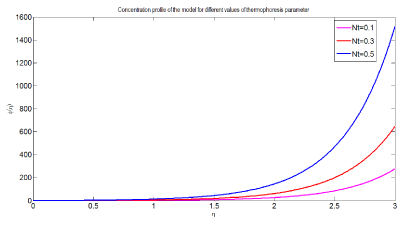
Figure 11 depicts variation of concentration profile of the model in response to a change in thermophoresis parameter. The graph is plotted versus for different values of dimensionless concentration on the vertical axis and dimensionless distance on the horizontal axis. From the simulation study it can be observed that as thermophoresis parameter increases concentration of nanoparticles of the model increases. Consequently concentration boundary layer thickness increases. Physiologically, this can be interpreted as nanoparticles can diffuse quickly in the arterial vessel.

Conclusion

Theoretical and numerical analysis have been investigated on the effect of nanoparticles on MHD blood flow in porous arterial vessel with the influence of thermal radiation, chemical reaction and heat generation/ absorption. The non linear partial differential equations are converted to ordinary differential equations using similarity transformations which are solved numerically.

The following important results are obtained from the simulation study:

i. An increment in unsteadiness and permeability parameter results in an increment of velocity profile of the model problem.

ii. As Hartmann number increases velocity profile of the model decreases.

iii. As Brownian motion parameter, thermophoresis parameter, thermal radiation parameter and heat source parameter increases temperature profile of the model problem increases.

iv. An increment in Lewis number and chemical reaction parameter results in decrement of nanoparticles concentration of the nanofluid.

v. As the values of thermophoresis parameter increases nanoparticles concentration of the nanofluid increases.

Application of the Model Problem in Medical Science

The numerical results of the present study are compared with Ferdows, et al. (2012) and Bidin and Nazar, et al. (2009) in order to check the validity of the present work. Thus the results are in good agreement with mentioned literature reviews.

Blood is considered as non-Newtonian fluid, the small sized nanoparticles have very wide application in biomedical application.

i. Nanoparticles like gold can be applied to activate or prevent growth of blood vein (Hatami M, HatamiJ,Ganji DD[2014]).

ii. To enhance or reduce blood capillary growth in some specified diseases some drugs are applied but efficient for short time. Recently researchers revealed that nanoparticles are effective in drug carrying and delivery vehicles because large quantities of therapeutic molecules are encapsulated in them (Rahbari A, Fakour M, Hamzehezhad A, Vakilabadi MA, Ganji DD [2017]).

iii. In this study the effect of nanoparticles on MHD blood flows of arterial porous vessel with the influence of thermal radiation, chemical reaction and heat generation/absorption.

Nomenclature

unsteadiness parameter

velocity of the nanofluid flow along x axis of the arterial vessel

transverse velocity of nanofluid flow in arterial porous vessel

temperature of blood at any point in the arterial porous vessel

concentration of nanoparticles of the blood at any point in the arterial porous vessel

streching velocity of arterial porous vessel of blood flow

nanoparticles concentration of blood along the x axis

temperature of arterial porous vessel wall

ambient temperature of the medium

ambient nanoparticles concentration of the solute

effective heat capacity of the nanoparticles

effective heat capacity of the fluid

time dependent magnetic field intensity

Brownian diffusion coefficient

thermophoresis diffusion coefficient

Lewis number

thermophoresis parameter

Brownian motion parameter

time dependent permeability of arterial porous vessel

constant permeability of arterial porous medium

non-dimensional permeability of arterial porous medium parameter

radiative heat flux of blood

$M-$ Hartmann number of blood

prandtl number

radiative parameter

time dependent chemical reaction of nanoparticles of arterial blood vessel

thermal conductivity of nanoparticles of arterial blood vessel

stream function

heat generation/absorption of the arterial vessel

dimensionless temperature

the ratio of heat capacity of nanoparticles to the fluid

electrical conductivity of fluid

density of fluid

density of nanoparticles

$v-$ kinematic viscosity of blood

dynamic viscosity of blood

dimensionless similarity variable

dynamic viscosity

References

1. Ogulu A, Amos E (2007) Modeling Pulsatile blood flow within a homogeneous porous bed in the presence of a uniform magnetic field and time dependent suction. Int Commun Heat Mass Transfer 34: 989-995.
2. Majhi SN, Nair VR (1994) Pulsatile flow of third grade fluids under body acceleration modeling blood flow. Int J Eng Sci 32: 839-846.
3. Zaman A, Ali N, Sajid M (2017) Numerical Simulation of Pulsatile flow of blood in a porous saturated overlapping stenosed artery. Math Comput Simul 134: 1-16.
4. Buongiorno J (2006) Convective transport in nanofluids. J Heat Transfer Trans ASME 128: 240-250.
5. Makinde OD, Aziz A (2011) Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int J Thermal Sci 50: 1326-1332.
6. Gorla RSR, Kumari M (2011) Mixed convection flow of a non Newtonian nanofluid over a non-linearly stretching surface. J Nanofluids 1: 186-195.
7. Mabood F, Khan WA, Ismail AIM (2015) MHD boundary layer flow and heat transfer of nanofluid over a nonlinear stretching sheet: A numerical study. J Magn Magn Mater 374: 569-576.
8. Hakeem AKA, Ganesh NV, Ganga B (2015) Magnetic field effect on second order slip flow of nanofluid over stretching/shrinking with thermal radiation effects. J Magn Magn Mater 381: 243-257.
9. Sheikh M, Abbas Z (2015) Effects of thermophoresis and heat generation/absorption on MHD flow due to an oscillatory stretching sheet with chemically reactive species. J Magn Magn Mater 396: 204-213.
10. Sheikholeslami M, Ganji DD, Javed MY, et al. (2015) Effect of thermal radiation on MHD nanofluid flow and heat transfer by means of two phase model. J Magn Magn Mater 374: 36-43.
11. Rashidi MM, Ganesh NV, Hakeem AKA, et al. (2014) Buoyancy effect on MHD flow of nanofluid over a stretching sheet in the presence of thermal radiation. J Mol Liq 198: 234-238.
12. Chamkha AJ, Issa C (2000) Effects of heat generation/absorption and thermophoresis on hydromagnetic flow with heat and mass transfer over a flat surface. Int J Numer Method Heat Fluid Flow 10: 432-449.
13. Srinivas Maripala, Kishan N (2015) Unsteady MHD flow and heat transfer of nanofluid over a permeable shrinking sheet with thermal and chemical reaction. American Journal of Engineering 4: 1-12.
14. B Zigta, PR Koya (2017) The Effect of MHD on Free Convection with periodic Temperature and Concentration in The Presence of Thermal Radiation and Chemical reaction. International Journal of Applied Mechanics and Engineering 22: 1059-1073.
15. B Zigta (2018) The Effect of Thermal Radiation, Chemical reaction and Viscous Dissipation on MHD Flow. Int J Applied Mechanics and Engineering 23: 787-801.
16. B Zigta (2019) Thermal Radiation, Chemical Reaction, Viscous and Joule dissipation Effects on MHD Flow Embedded in a Porous Medium. Int J Applied Mechanics and Engineering 24: 725-737.
17. B Zigta (2020) Mixed Convection on MHD Flow with Thermal Radiation, Chemical Reaction and Viscous Dissipation Embedded in a Porous Medium. Int J Applied Mechanics and Engineering 25: 219-235.
18. B Zigta (2020) Effect of Thermal Radiation and Chemical Reaction on MHD Flow of Blood in Stretching Permeable Vessel. Int J Applied Mechanics and Engineering 25: 198-211.
19. Mohamed R Eid (2016) Chemical reaction effect on MHD boundary layer Flow of Two phase nanofluid model over an exponentially stretching with a heat generation. Journal of molecular fluids 220: 718-725.