Oseen's Correction to Stokes Drag in the Perspective of Newtonian and Micro-polar Fluid: A Technical Note
Abstract
A technical note on Oseen's correction to Stokes drag on axially symmetric body is written. The previous published work of author [1,2] [Srivastava and Srivastava (2017)] has been utilized for the purpose. Brenner's (1961) formula for Oseen's correction to Stokes drag on axially symmetric particle placed in axial uniform flow of Newtonian fluid is advanced for transverse flow configuration. The relationship between Oseen's drag in both flow configurations for axially symmetric particle is generated for Newtonian fluid and advanced for Micro-polar fluid later on. In the end, the results are validated and tested for spherical body.
Keywords
Stokes drag, Axially symmetric body, Oseen's correction, Newtonian fluid, Micro-Polar fluid
Introduction
The theory of low Reynolds number hydrodynamics has great importance in the study of Geophysical flow and Physiological flow. In low Reynolds number hydrodynamics, the mathematicians, engineers and physicists are always interested in knowing the correct value of drag experienced by particle moving uniformly through the infinite fluid. In eighteenth century, it was George Gabriel Stokes (1851) who gave an idea popularly known as Stokes approximation to obtain the drag on moving sphere by neglecting the fluid inertia in the vicinity of the particle. Later on, this drag formula is known as Stokes law. In nineteenth century, Oseen (1927) gave an idea of Oseen's approximation by considering the effect of fluid inertia in the vicinity of particle neglected by Stokes earlier. In Oseen's expression of drag, the first order term of size (3/8) Re, Re is Reynolds number, is also present. The complete form expression of Oseen's drag on sphere is
D = D0[1 + (3/8)Re], (1.1)
where D0 = 6πµUa is Stokes drag on sphere of radius 'a' moving through the fluid with uniform velocity 'U' and µ, the fluid viscosity. This expression of drag is called the Oseen's correction to Stokes drag on sphere. After this development, there are many other authors who initiated and contributed in this direction to find the general expression of Stokes drag on axially symmetric particle. For example- Payne and Pell [3] gave a closed form expression of drag for class of axially symmetric bodies in terms of stream function. Chwang and Wu (Part-2, 1975) provided the general and closed form expression of drag on axially symmetric particle in terms of fundamental singularities. In order to correct the Stokes drag on class of axially symmetric bodies within the limit of Oseen's approximation, it was Howard Brenner (1961) who found the Oseen resistance of a particle of arbitrary shape placed in axial uniform Stokes flow of Newtonian fluid. The concept of micro-polar fluid comes into the picture when it has been introduced first by [4]. In this widely used theory, a continuum is regarded as consisting of structured particles, which not only contain mass and velocity but also a substructure, and which can support couple stresses and body couples. Similar to the work of [3] and Chwang and Wu (Part-2, 1975), [5] established the general closed form expression of Stokes drag on axially symmetric bodies placed under uniform flow of micro-polar fluid in terms of stream function. Shu and Lee [6] established the fundamental solution for Stokes drag on axially symmetric small particle placed under micro-polar fluid. Srivastava, et al. (2013) extended the work of Brenner (1961) by utilizing the DS-conjecture [1] and gave the expression of Oseen's correction to Stokes drag on axially symmetric bodies placed under transverse uniform flow of Newtonian fluid. Later on, Srivastava, et al. [2] provided the expression of Oseen's correction to Stokes drag on axially symmetric bodies placed under axial and transverse uniform flow of micro-polar fluid. Recently, Srivastava and Srivastava [7] provided the complete review on Oseen's correction to Stokes flow on axially symmetric particle for both type of fluid. Apart from these referred work, author would also like to refer two most prominent research books of Happel and Brenner [8] and Kim and Karrila [9] involving in depth literature on Stokes drag and couple.
In the present work, the authors aim is to establish the relationship between Oseen's drag in both axial and transverse flow configurations for axially symmetric particle by utilizing the DS-conjecture [1] for Newtonian as well as Micro-polar fluid. Author claim that this relationship must be satisfied for Oseen's drag on axially symmetric bodies in both flow configurations under the limitations of DS-conjecture [1].
Oseen's Drag on Axially Symmetric Particle in Newtonian Fluid
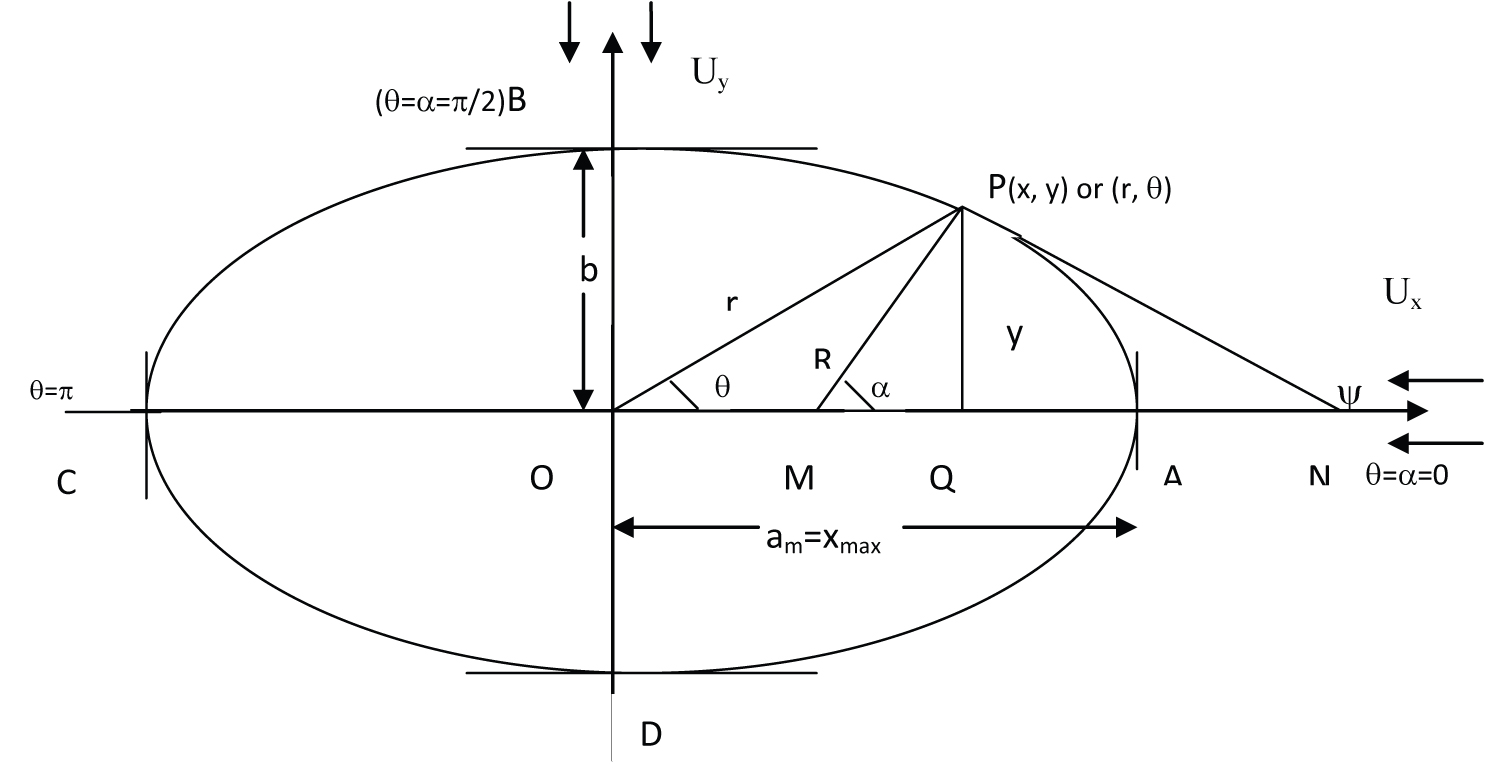
Datta and Srivastava [1] gave the expressions of Stokes drag on axially symmetric particle of revolution of curve in meridional plane with the condition of continuously turning tangent (Figure 1) in axial flow (along x-axis) as
Datta and Srivastava [1] Gave the expressions of Stokes drag on axially symmetric particle of revolution of curve in meridional plane with the condition of continuously turning tangent (Figure 1) in transverse flow (perpendicular to axis of symmetry, y-axis) as
In the above formulae, variable R is the intercepting length of normal between axis of symmetry and point on body curve in meridional plane and α is the angle made by normal from axis of symmetry. Also, hx and hy represents the height of centre of gravity of force system in both the flow configurations and 'b' is the semi-transverse length of body curve in merdional plane xy and 'µ' is the viscosity coefficient [1]. In every body-fluid interaction problems in fluid dynamics, the important quantity to evaluate is the drag experienced by body which in traditional approach always found as a solution of linear Stokes equation under no-slip boundary condition [8].
The relation between hx and hy (by using equations 2.1 and 2.2) is
The relation between Stokes drag in both axial flow and transverse flow cases (by using equations 2.1 and 2.2 and Ux= Uy= U) of Newtonian fluid is
If F be the Oseen's drag (Oseen's correction to Stokes drag), then by Brenner's formula (1964)
Brenner [8] obtained the Oseen's correction (2.5) to Stokes drag on arbitrary particle placed under uniform axial flow of Newtonian fluid by solving the Oseen's equation [7] with no-slip boundary conditions.
From equations (2.4) and (2.5), we can easily get the relationship between Oseen's correction to Stokes drag on axially symmetric bodies placed under uniform axial flow and transverse flow of Newtonian fluid as
Where F/Fx and F/Fy are the Oseen's correction to Stokes drag (Fx and Fy) on axially symmetric particle placed under uniform axial and transverse flow.
Sphere
Let us consider the sphere of radius 'b', then R = b and Fx= Fy= 6πµUb and from relationship (2.6), it can be easily verified that
This clearly indicates that Oseen's correction to Stokes drag on sphere is same for both the flow configurations in Newtonian fluid. So, the relationship (2.6) is validated for spherical body. The relationship may be verified for other axially symmetric particle as well.
Oseen's Drag on Axially Symmetric particle in Micro-Polar Fluid
Srivastava and Srivastava [2] gave the expressions of Stokes drag on axially symmetric particle of revolution of curve in meridional plane with the condition of continuously turning tangent (Figure 1) in axial flow (along x-axis) as
Srivastava and Srivastava [2] gave the expressions of Stokes drag on axially symmetric particle of revolution of curve in meridional plane with the condition of continuously turning tangent (Figure 1) in transverse flow (perpendicular to axis of symmetry, y-axis ) as
In the above formulae, variable R is the intercepting length of normal between axis of symmetry and point on body curve in meridional plane and α is the angle made by normal from axis of symmetry and hx and hy represents the height of centre of gravity of force system in both the flow configurations and 'b' is the semi-transverse length of body curve in meridional plane xy, 'µ' is the viscosity coefficient and k is the micro-polarity parameter. In every body-fluid interaction problems in fluid dynamics, the important quantity to evaluate is the drag experienced by body which in traditional approach always found as a solution of linear Stokes equation under no-slip and no-spin boundary condition [2].
The relation between hx and hy (by using equations 2.1 and 2.2) is
Equation (4.3) clearly indicates that the relationship between hx and hy is independent to the viscosity of fluid and micro-polarity of micro-polar fluid but depends on variables R and α related to axis-symmetric particle. The relation between Stokes drag in both axial flow and transverse flow cases (by using equations 2.1 and 2.2) of micro-polar fluid is
It is interesting to note that the relationship between centre of gravity of force systems in Newtonian fluid (equation 2.3) and micro-polar fluid (equation 4.3) remains same. It means that the relationship is independent to the viscosity and micro-polarity of either fluid but the drag relationship (equation 4.4) in micro-polar fluid differs only with µ+k in place of µ in the drag relationship in Newtonian fluid [2].
Sphere
Let us consider the sphere of radius 'b', then R= b and Fx= Fy= 6π(µ+k)Ub and from relationship (4.4), we can easily get
This clearly indicates that Oseen's correction to Stokes drag on sphere is same for both the flow configurations in micro-polar fluid. So, the relationship (4.4) is verified for spherical body. The relationship may be verified for other axially symmetric particle as well.
Conclusion
The relationship between Oseen's drag in both axial and transverse flow configurations for axially symmetric particle is obtained by utilizing the DS-conjecture [1] followed by Brenner's formula (1964) for Newtonian as well as Micro-polar fluid. Author claim that this relationship must be satisfied for Oseen's drag on axially symmetric bodies in both flow configurations under the limitations of DS-conjecture [1]. It is interested to note that the proposed relationship is independent to the viscosity and micro-polarity of either fluid but the drag relationship (equation 4.4) in micro-polar fluid differs only with µ + k in place of µ in the drag relationship in Newtonian fluid [2]. Author claims that this technical note on Oseen's correction will open the doors for researchers to study the properties and features of both the fluid.
Acknowledgement
Author convey his sincere thanks to the authorities of B.S.N.V. Post Graduate College, Lucknow, to provide basic infrastructure facilities and moral support through out to carry out research work.
References
- Datta S, Srivastava DK (1999) Stokes drag on axially symmetric bodies: A new approach. Proceedings Math Sci 109: 441-452.
- Srivastava DK, Yadav RR, Srivastava N (2016) Oseen's correction to Stokes drag on axially symmetric bodies in micro polar fluid. IJAAMM 3: 41-78.
- Payne LE, Pell WH (1960) The Stokes flow problem for a class of axially symmetric bodies. J Fluid Mech 7: 529-549.
- Eringen AC (1966) Theory of micro polar fluids. J Math Mech 16: 1-18.
- Ramkissoon H, Majumdar SR (1976) Drag on an axially symmetric body in the Stokes flow of micro polar fluid. Physics of Fluids 19: 16-21.
- Shu J-J, Lee JS (2008) Fundamental solutions for micro polar fluids. J Engng Math 61: 69-79.
- Srivastava DK, Srivastava N (2018) Oseen's correction to Stokes drag revisited. International Journal of Current Advanced Research 7.
- Happel J, Brenner H (1964) Low Reynolds Number Hydrodynamics, Nijhoff, Dordrecht. The Nederlands.
- Kim S, Karrila SJ (2005) Microhydrodynamics: Principles and Selected Applications, Courier Corporation.
Corresponding Author
Deepak Kumar Srivastava, Department of Mathematics, University of Lucknow, B.S.N.V. Post Graduate College (KKV), Station Road, Charbagh, Lucknow-226001, U.P, India.
Copyright
© 2021 Srivastava DK. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.