Operation of Rectangular Jet using a Rectangular Notch at the Midspan

Abstract

The mean and turbulent flowfields of turbulent jet issuing from a rectangular nozzle (AR: Aspect Ratio = 12.5) with a rectangular notch at the midspan, have been investigated, experimentally. The object of this experiment is to investigate a possibility of the operation of both the mean and the turbulent velocity fields in the rectangular jet field by the attachment of a rectangular notch perpendicular to the rectangular jet. Four notch aspect ratios (NAR: Notch Aspect Ratio) of the rectangular notch used were 2.5, 7.5, 12.5 and 165, respectively. The Reynolds number based on the nozzle width d and the exit mean velocity U_e, was kept constant 30000 (NAR = 2.5 and 7.5), 15000 (NAR = 12.5) and 13000 (NAR = 165), respectively. Longitudinal mean velocity and turbulent intensities were measured using an X-array Hot-Wire Probe operated by the linearized constant temperature anemometers (DANTEC), and the spanwise and the lateral mean velocities were measured using a yaw meter. Signals from the anemometers were passed through the low-pass filters and sampled using A.D. converter. Processing of the signals was made by a personal computer. The results obtained lead to the conclusions that the inward secondary flow velocities toward the jet centre region both on the rectangular jet axis and the rectangular notch axis in the upstream region are found for the cases of NAR ≥ 2.5, and the magnitude of the inward secondary flow velocity on the z axis can be operated by the value of NAR. Furthermore, the potential core length of NAR = 12.5 takes the longest value in all NAR cases. The attachment of a rectangular notch perpendicular to the rectangular nozzle suppresses the development of the turbulent velocity scales near the jet centre in the upstream region depending on the value of NAR due to the inward secondary flow velocity on both the y and z axes.

Keywords

Operation, Rectangular jet, Rectangular notch, Secondary flow, Passive operation, Mean and turbulent velocity fields, Contour Plot

Introduction

The mean and turbulent flow fields of turbulent jet issuing from the rectangular nozzle with a rectangular notch at the midspan, have been investigated, experimentally. The object of this experiment is to investigate a possibility of the operation of both the mean and turbulent velocity fields in the rectangular jet by the attachment of a rectangular notch perpendicular to the rectangular jet.

The rectangular jet is very useful in many cases for which the improvement of the entrainment rate or the promotion of mixing [1,2] is necessary. However, in the cases of the employment of the rectangular jet to the engineering fields, the elongation of the jet flow is expected in many industrial situations, for example the washing in liquid by multiple parallel jets, the uniform plating technique [3], the acid washing process of rolling mill and the air curtain (air shield and ventilating).

To these technical assignments, extension of the potential core length and suppression of the turbulent intensities seem to be effective methods.

So far, Trentacoste and Sforza [4], Sforza and Stasi [5], Krothapalli, Baganoff and Karamcheti [6], Quinn [7] classified the flowfield of the rectangular jet into 3 regions such as Potential Core region (PC region), Characteristic Decay region (CD region) and Axisymmetric Decay region (AD region). Furthermore, Marsters and Fotheringham [8] clarified that the longitudinal mean velocity profiles on the rectangular long axis showed the saddle-back shape which was caused by the inward secondary flow on the long axis, and the reduction rate of the longitudinal mean velocity along the jet centreline showed the typical feature in the cases of AR (Aspect Ratio) ≤ 6.44. From the results mentioned above, it is supposed that the variation of AR changes the PC length and eases the velocity reduction rate of CD region for the rectangular jet.

On the other hand, Fujita, et al. reported that the PC length of the finite cruciform jet [9] showed the largest value for AR = 12.5 and this result was caused by the inward secondary flow toward the jet centre region on the two representative jet axes [10]. Quinn and Marsters [11] also reported the promotion of PC length for the finite cruciform jet with finite axis length (AR = 11.97). Furthermore, the reports relative to the present study were carried out by many researchers [12-16].

From these results, it is expected that the attachment of a rectangular notch perpendicular to the rectangular jet will promote the magnitude of the inward secondary flow toward the jet centre region on the rectangular jet axis [10] and suppress the turbulent intensities near the jet centre in the upstream region, significantly.

In this report, the mean and turbulent velocity fields of turbulent jet issuing from the rectangular nozzle (AR = 12.5) with a rectangular notch (NAR = 2.5, 7.5, 12.5 and 165 [14]) at the midspan, have been investigated (Figure 1).

Nomenclature

AR : Aspect ratio of the rectangular nozzle (= h/d)

d : Nozzle width of the rectangular nozzle and the rectangular notch

h : Nozzle length of the rectangular nozzle

l : Nozzle length of the rectangular notch

NAR : Aspect ratio of the rectangular notch (= l/d)

q : Turbulent kinetic energy $\left(={\left(\overline{{\mu }^2}+\overline{{\nu }^2}+\overline{w^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)$

q_uv : Turbulent kinetic energy $\left(={\left[\left(3/2\right)\left(\overline{{\mu }^2}+\overline{{\nu }^2}\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)$

Re : Reynolds number $\left(=U_{e^{•}}d/v\right)$

U : Longitudinal mean velocity

U_e : Longitudinal mean velocity at the nozzle centre of the exit plane

U_ox : Longitudinal mean velocity on the x axis

u : Longitudinal fluctuating velocity

V : Lateral mean velocity

v : Lateral fluctuating velocity

W : Spanwise mean velocity

w : Spanwise fluctuating velocity

x, y, z : Cartesian coordinate system with origin at the nozzle centre of the exit plane (x/d=0)

Subscripts

e : Value at the nozzle centre of the exit plane

ox : Value on the x axis

rms : Root Mean Square

Experimental Setup and Procedure

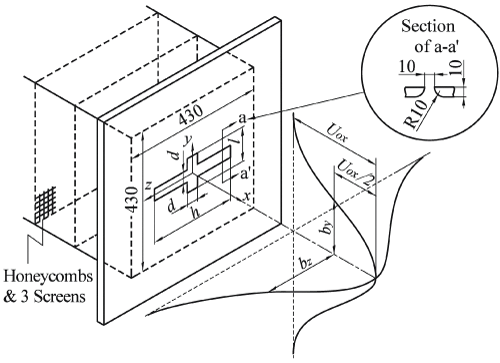
The configuration of the flowfield and the coordinate system are presented in Figure 1. The rectangular nozzle with a rectangular notch is installed at the end of settling chamber. The jet flow facility consists of a turbo fan, a settling chamber fitted with honeycomb and mesh wire screens, and the rectangular nozzle with a rectangular notch. The main axis length h and the width d of the rectangular nozzle are 125 mm and 10 mm (AR = 12.5), respectively. On the other hand, the main axis length l of the rectangular notch is 25 mm (NAR = 2.5), 75 mm (NAR = 7.5) and 125 mm (NAR = 12.5) respectively, and each notch width d is 10 mm. For NAR = 165, another experimental equipment [14] was used, and the rectangular notch length l and the width d were 990 mm and 6 mm (NAR = 165) [14], respectively. Here, the value of NAR for the rectangular nozzle [10] was defined as NAR = 0 expediently and this rectangular nozzle was used to compare with another case of NAR.

Longitudinal mean velocity and turbulent intensities were measured using an X-array Hot-Wire Probe (d_h = 5.0 µm in diameter, l_h = 1.0 mm effective length: l_h/d_h = 200) operated by the linearized constant temperature anemometers (DANTEC), and the spanwise and the lateral mean velocities were measured using a yaw meter. Signals from the anemometers were passed through the low-pass filters (10 kHz) and sampled using A.D. converter at 20 kHz. Processing of the signals was made by a personal computer. Acquisition time of the signals was usually 80 seconds. The exit plane Reynolds number based on the nozzle width d and the exit mean velocity U_e, was kept constant 30000 (NAR = 2.5 and 7.5), 15000 (NAR = 12.5) and 13000 (NAR = 165) throughout the present experiment, respectively. And values of the nozzle exit turbulent intensity u_rms/U_e for all the NAR cases were about 0.4 × 10^-2. In this experiment, an uncertainty associated with the longitudinal mean velocity U is estimated at ± 3% of U_e, which includes calibration error of the linearized constant temperature anemometers, and that of the lateral mean velocity V and the spanwise mean velocity W at ± 6% of U_e, which includes calibration error of the yaw meter. Furthermore, an uncertainty for the turbulent intensities is ± 5.6 % of U_e.

Experimental Results and Discussion

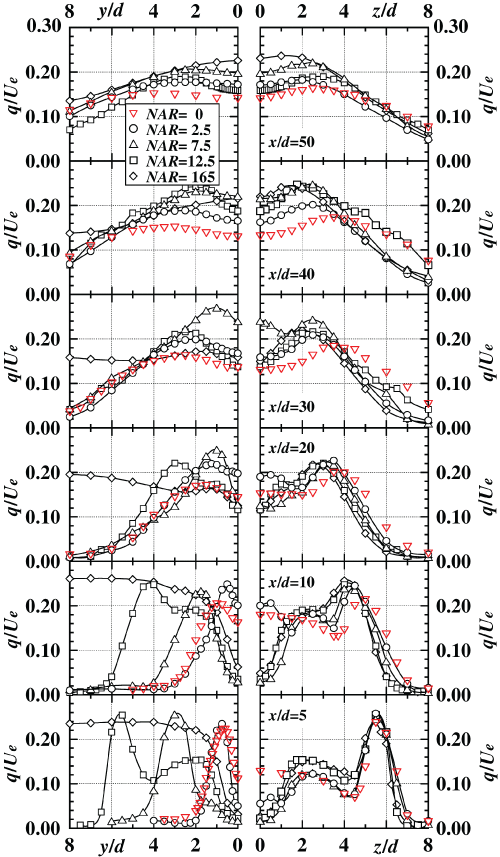
Streamwise variation of the longitudinal mean velocity profiles

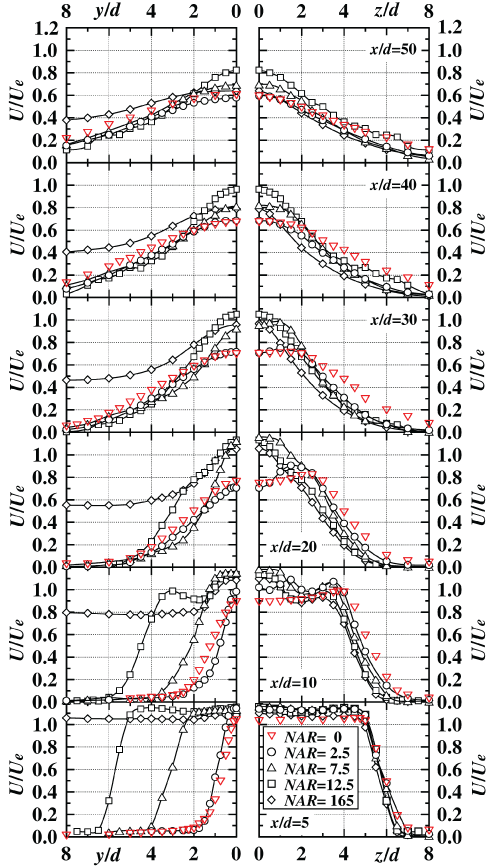
Figure 2 shows streamwise variation of longitudinal mean velocity profiles for all the NAR cases on both the y and z axes, respectively.

The profiles on the z axis at the section of x/d = 5 for all the NAR cases show each potential core region (U_ox/U_e ≤ 1.0) and saddle-back shape. For the case of NAR = 0 (rectangular nozzle), the profile at the section of x/d = 10 has only one peak at the jet edge. On the other hand, all the profiles for NAR ≤ 2.5 have two peaks both at the jet edge and the jet centre. The peak locations near the jet edge for all the NAR cases at x/d = 10 move toward the jet centre region compared with those of the section of x/d = 5, because mean flow kinetic energy were transported toward the jet centre region by the inward advection transport term $\left(W\partial \left(U^2/2\right)/\partial z\right)$ [9] on the z axis as will be mentioned in Figure 3. In the region of x/d ≤ 20, peak locations for NAR = 0 and 2.5 still move toward the jet centre region by the inward secondary flow same as the result of x/d = 10.

For NAR = 2.5, 7.5 and 12.5, the profiles on the y axis (notch axis) at the section of x/d = 5 show each potential core region (U/U_e ≤ 1.0). However, the profile for NAR =165 shows potential core region on all the y axes. At the section of x/d = 10, profiles for NAR = 12.5 and 165 show saddle-back shape because of the same reason as the result on the z axes. Furthermore, in the region of x/d ≤ 20, all profiles show monotonous decrease from the value at the jet centre (y/d = 0) to the notch jet edge.

From the mentioned, it is clarified that adding a rectangular notch, the longitudinal mean velocity profiles on the rectangular nozzle can be changed by the value of NAR due to the inward secondary flow.

Streamwise variation of the secondary flow velocity profiles

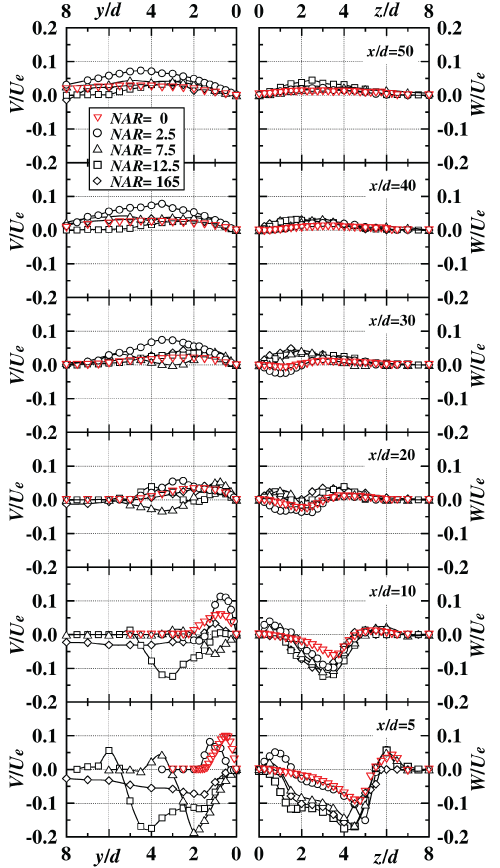
Figure 3 presents secondary flow velocity profiles on both the y and z axes for all the NAR cases, respectively.

All the profiles on the z axis at the section of x/d = 5 show each inward secondary flow velocity. The magnitude of the inward secondary flow velocity for NAR ≤ 7.5 in the region of z/d < 5.0 is larger than that for NAR = 0 and 2.5. At the sections of x/d = 10 and 20, there are also inward secondary flows for all the NAR cases. All locations taking maximum value of the inward secondary flow velocity move toward the jet centre region. Finally at the sections of x/d ≤ 30, the inward secondary flow velocities are found only for NAR = 0 and 2.5 near the jet centre region at x/d = 30.

The profiles on the y axis at the section of x/d = 5, have inward secondary flows for the cases of NAR ≥ 2.5. However, the inward secondary flow for the case of NAR = 2.5 exists only at narrow region near the jet centre. On the contrary, the magnitude of inward secondary flow velocity for NAR = 7.5 and 12.5 takes large value. At the section of x/d = 10, locations taking maximum value of the inward secondary flow velocity profiles for NAR = 7.5 and 12.5 move toward the jet centre region. Therefore, if the strong inward secondary flow was needed on the notch axis in the upstream region, it can be seen that the magnitude of NAR is suitable to be between 7.5 and 12.5. Furthermore at the section of x/d = 20, there are still inward secondary flows for NAR = 7.5 and 12.5. Finally, at the section of x/d ≤ 30, there is no inward secondary flow in all the NAR cases.

From the results mentioned above, it is clarified that the magnitude of the inward secondary flow for NAR = 7.5 and 12.5 on the z axis in the upstream region, show the larger values compared with those of NAR = 0 and 2.5. Therefore, the magnitude of the inward secondary flow on the z axis can be operated by the value of NAR.

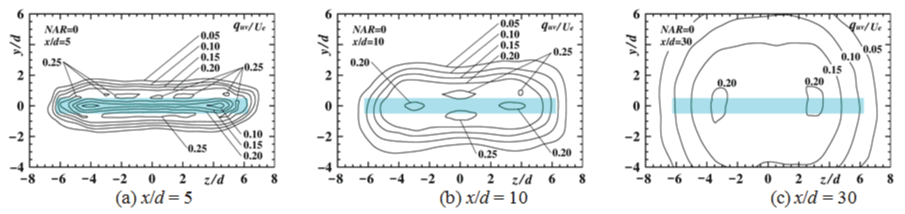
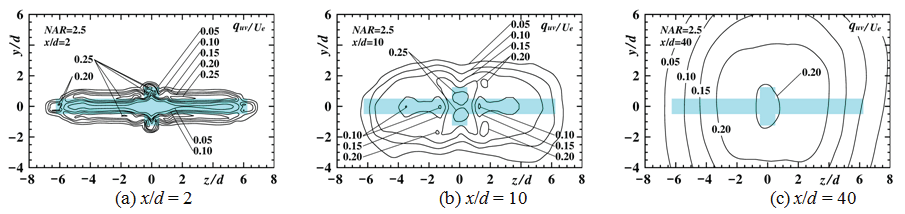
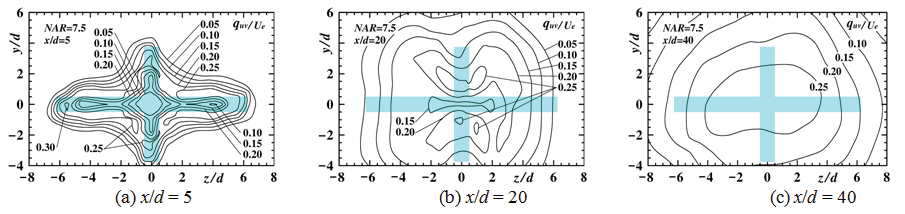
Contour plots of longitudinal mean velocity

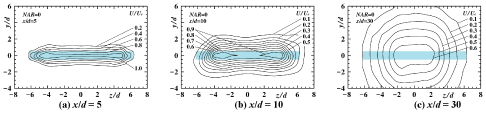
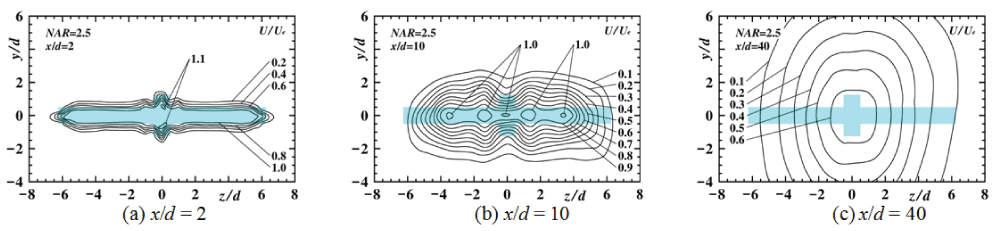
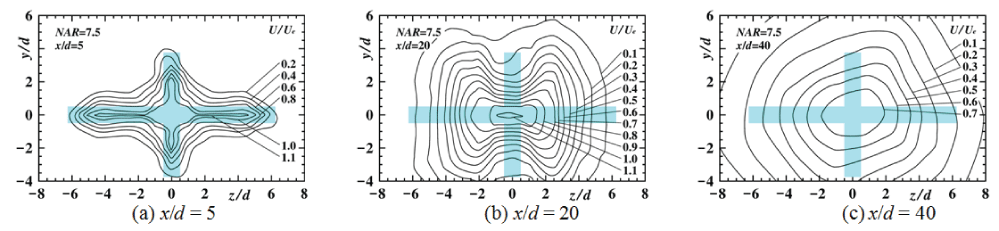
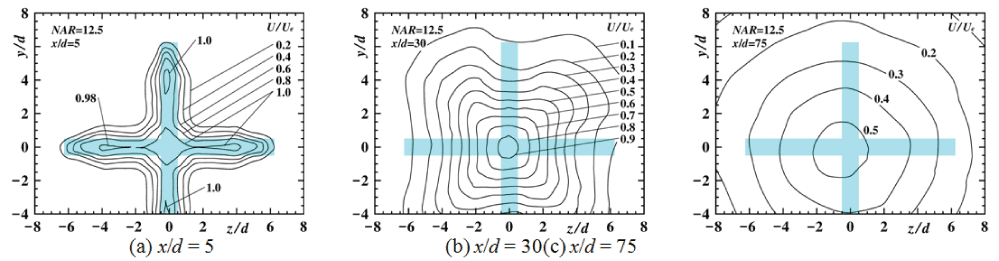
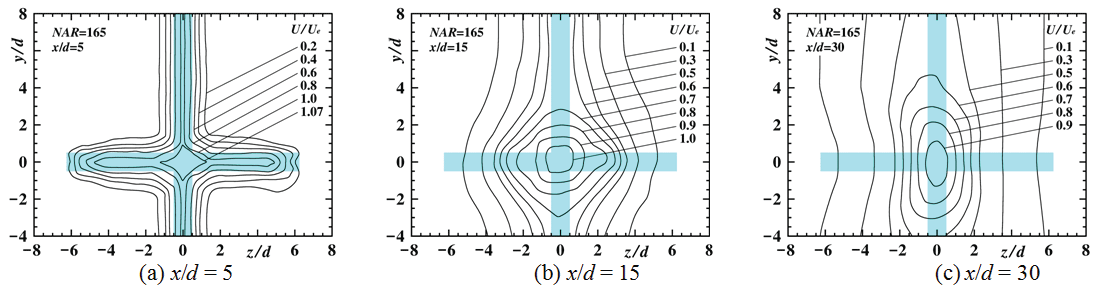
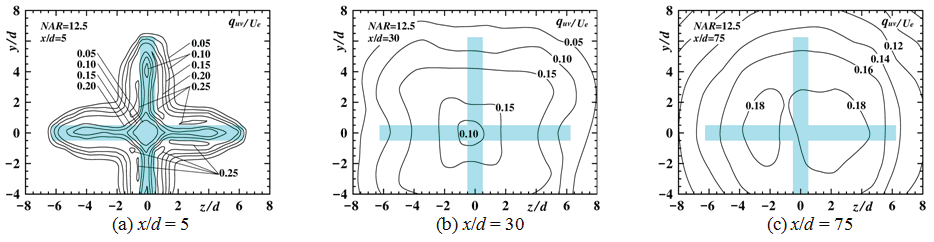
Streamwise variation of contour plots of U/U_e in the upstream region for NAR = 0, 2.5, 7.5, 12.5 [10] and 165 [14] are shown in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 to indicate streamwise variation of each jet field, respectively. Here, each nozzle shape at the nozzle exit plane is painted blue in each figure.

Configuration of the contour plot at the section of x/d = 5 for NAR = 0 indicates almost the rectangular shape close to the rectangular nozzle outer shape. Next, the width of the contour plot of U/U_e = 0.6 on the z axis at x/d = 10 shows smaller one compared with that of x/d = 5 because of the inward secondary flow as shown in Figure 3. Finally at the section of x/d = 30, the shape of contour plot shows almost the circular shape due to the outward flow on the z axis.

For NAR = 2.5, the contour plot at the section of x/d = 2 also shows almost the nozzle outer shape with outward prominence parallel to the y axis on z/d ≅ ± 1.0 slice planes. At the section of x/d = 10, the width of the contour plot of U/U_e = 0.6 on the z axis at the section of x/d = 10 shows smaller one compared with that of x/d = 5 because of the same reason. At the section of x/d = 40, the contour plot becomes an elliptic shape because of the strong outward flow on the y axis as shown in Figure 3.

For NAR = 7.5, the contour plot at the section of x/d = 5 shows a cruciform shape similar to the nozzle outer shape. At the section of x/d = 20, the width of the contour plot of U/U_e = 0.6 on both the y and z axis show smaller value compared with those of x/d = 5 because of the inward secondary flow as shown in Figure 3. The contour plot at the section of x/d = 40, shows a diamond shape due to the outward flow on both the y and z axes.

The contour plot at the section of x/d = 5 for NAR = 12.5, shows a cruciform outer shape with a good symmetry. At the section of x/d = 30, the shape of the contour plot shows a cruciform shape with long axes on both the y = ± z axes and the width of the contour plot of U/U_e = 0.6 on both the y and z axis indicate the smaller values due to the inward secondary flow on both the y and z axes. At the section of x/d = 75, the contour plot shows a circular shape.

The contour plot at the section of x/d = 5 for NAR = 165, shows a shape close to the nozzle outer shape. At the section of x/d = 15, the width of the contour plot of U/U_e = 0.6 on the z axis becomes smaller than that of x/d = 5 due to the inward secondary flow.

From the above, it is clarified that the width of the contour plot for NAR = 7.5 and 12.5 were especially restricted by the strong inward secondary flow on the z axis.

Comparison of secondary flow vectors

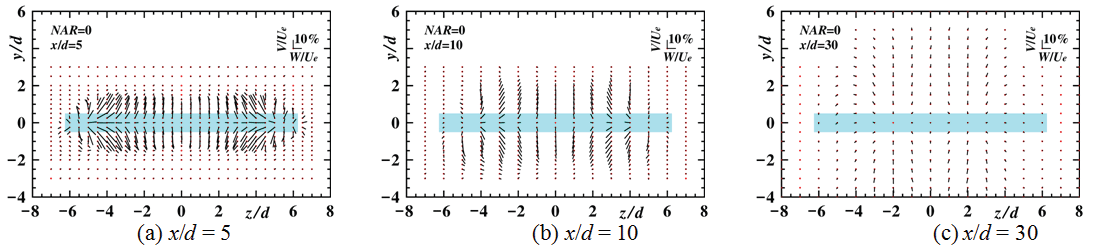
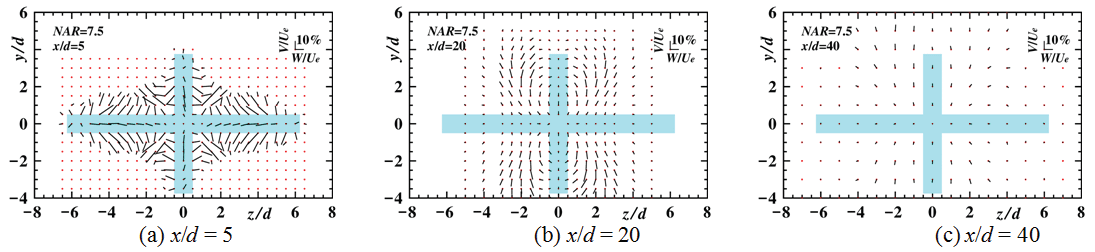
Streamwise variation of secondary flow vectors are shown in Figure 9 and Figure 10 to clarify the difference of both the magnitude and the direction of the secondary flow velocity between the rectangular jet (NAR = 0) and the rectangular jet with a rectangular notch (NAR = 7.5) as the representative of each NAR case.

For the case of NAR = 0, directions of the secondary flow vectors on the y axis are outward at all sections of x/d = 5, 10 and 30. On the other hand, directions of the secondary flow vectors near the ends of the rectangular nozzle on the z axis, are inward at the sections of x/d = 5 and 10. This result was the same as found in the reports [5,7].

For the case of NAR = 7.5, the secondary flow vectors on both the y axis (notch axis) and the z axis (rectangular nozzle axis) at x/d = 5 show the inward direction, and the magnitude of the inward secondary flow vectors on the z axis shows larger values compared with that of NAR = 0. At the section of x/d = 20, there are small inward secondary flow vectors near the end of rectangular notch. At the section of x/d = 40, there are no inward secondary flow vectors on both the y and z axes.

From the mentioned above, it is clarified that the inward secondary flow vector on the rectangular nozzle axis of NAR = 7.5 is promoted in the upstream region compared with that of the rectangular jet (NAR = 0), by the attachment of a rectangular notch perpendicular to the rectangular nozzle.

Velocity scale and length scale

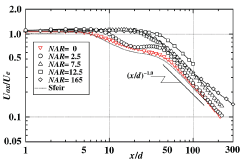
Figure 11 shows streamwise variations of the longitudinal mean velocity U_ox/U_e on the x axis for all NAR cases. The result of the rectangular jet (AR = 10) by Sfeir [17] is also plotted in the same figure for comparison. All PC length of the rectangular jet with a rectangular notch for NAR ≤ 2.5, take larger values compared with that of the rectangular jet (NAR = 0). This reason is explained as that there are the advection transports of mean kinetic energy $\left(W\partial \left(U^2/2\right)/\partial Z\right)$ on the z axis and ($V\partial \left(U^2/2\right)/\partial y$ on the y axis) [10] toward the jet centre region by the inward secondary flow velocity on both the z (the rectangular jet) and y (the rectangular notch) axes as shown in Figure 3. Furthermore, length of the PC region varies with the value of NAR and takes the longest one for NAR=12.5. This reason is explained as that the inward secondary flow for NAR = 12.5 takes the maximum value on both the z and the y axes as shown in Figure 3. From these results, it can be seen that the PC length of the rectangular jet with a rectangular notch can be operated by the variation of the value of NAR.

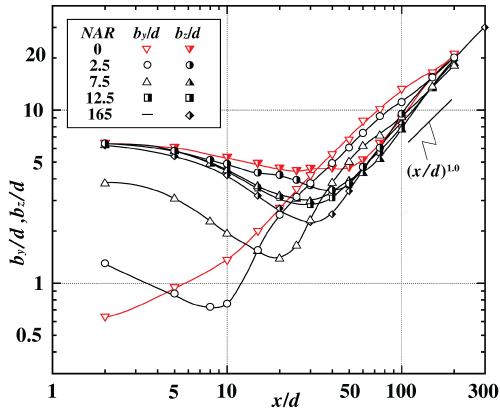
On the other hand, streamwise variation of half velocity width on both the y and z axes is shown in Figure 12 in order to examine an effect of the value of NAR on length scale. At first, all half velocity widths b_z/d on the z axis decrease from almost the same value at the section of x/d = 2, and they all take the minimum value at each streamwise section. These decreasing features are caused by magnitude of the inward secondary flow [10] as shown in Figure 3. These minimum values of b_z/d become smaller with increasing of the value of NAR, and the b_z/d for NAR = 165 takes the smallest value at x/d = 30. From these results, it can be seen that the development of the half velocity width b_z/d on the z axis can be operated by the variation of the value of NAR. On the other hand, the values of b_y/d for NAR = 2.5, 7.5 and 12.5 also decrease in the upstream region because of the inward secondary flow as shown in Figure 3 and take each minimum value at the sections of x/d = 8, 20 and 30, respectively.

Streamwise variation of turbulent kinetic energy profiles

Figure 13 shows streamwise variation of turbulent kinetic energy profiles on both the y and z axes for all the NAR cases, respectively.

On the z axis, all the profiles at x/d = 5 show almost the same shape except for NAR = 0 near the jet centre region and take maximum values near the jet edge (z/d ≅ ± 5.5). The values of the jet centre region for NAR ≤ 2.5 are smaller than that for NAR = 0. This result is explained as that fluid lumps having high longitudinal mean velocity and low turbulent revel in the potential core region (U/U_e ≤ 1.0) for NAR ≥ 2.5, are transported toward the jet centre region by the inward secondary flow on both the y and z axes as shown in Figure 3. In short, it is clarified that the attachment of a rectangular notch perpendicular to the rectangular nozzle suppresses the development of the turbulent kinetic energy near the jet centre of the upstream region, and the magnitude of the suppression effect depends on the value of NAR. Furthermore, the position of the maximum value for all NAR cases moved toward the jet centre region until the section of x/d = 30.

On the y axis, each profile at x/d = 5 except for NAR = 165, takes each local minimum value at the jet centre and maximum value near the region where each longitudinal mean velocity gradient shows the maximum value (see Figure 2). The profile of NAR = 165 indicates the minimum value at the jet centre (y/d = 0) and has almost a constant value in the region of y/d ≤ 4.0. At the section of x/d = 10, the magnitude of the value near the jet centre region for NAR ≤ 7.5 is kept small and suppressed compared with those for NAR = 0 and 2.5, this is the same reason as the result on the z axis. Then, the positions of the maximum value move toward the jet centre region except for NAR = 0. Furthermore, at the section of x/d = 20, the positions of the maximum value for NAR = 7.5 and 12.5 still move toward the jet centre region due to the inward secondary flow. In the region of x/d ≥ 30, the position of the maximum value move toward the outside on the y axis.

From the above, it is revealed that the attachment of a rectangular notch perpendicular to the rectangular nozzle suppresses the development of the turbulent kinetic energy near the jet centre in the upstream region, and the magnitude of the suppression effect depends on the value of NAR.

Contour plots of turbulent kinetic energy

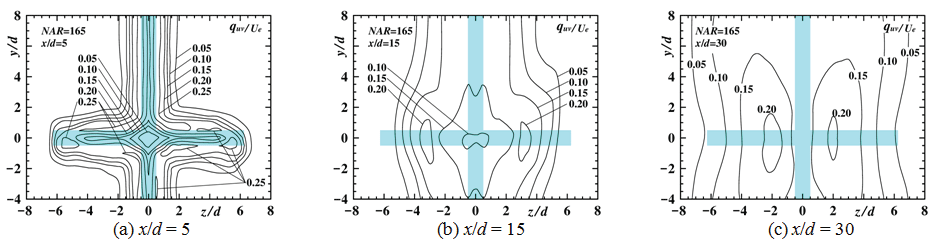
Contour plots of turbulent kinetic energy q_uv/U_e for all the NAR cases are shown in Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 to clarify the difference in the development of turbulent kinetic energy due to the effect of the inward secondary flow velocity on both the y and z axes. The contour plots of NAR = 0 are shown in Figure 14 as the basic plots to compare with another NAR cases.

For NAR = 2.5, the contour plot at x/d = 2 shows a rectangular shape with small prominent regions on the y axis and has the maximum value (q_uv/U_e ≤ 0.20) at z/d ≅ ± 6.0 on the z axis. At the section of x/d = 10, the locations of the maximum value at the section of x/d = 2 on the z axis, move to the locations of z/d ≅ ± 4.5 (q_uv/U_e ≤ 0.15) because of the inward secondary flow velocity. At the section of x/d = 30, the contour plot shows a circular shape.

For NAR = 7.5, the contour plot at x/d = 5 shows a cruciform shape and takes each maximum value at y/d ≅ ± 2.5 on the y axis and at z/d ≅ ± 5.5 on the z axis, respectively. The contour plot near the jet centre region shows a diamond-shaped region taking the local minimum value (q_uv/U_e ≤ 0.05). This reason is explained as that the development of turbulent kinetic energy is suppressed by the inward advection transports of the turbulent kinetic energy $\left(V\partial \left(q^2/2\right)/\partial y\right)$ on the y axis and ($W\partial \left(q^2/2\right)/\partial z$ on the z axis) as explained in Figure 13 Therefore, the value of the jet centre region for NAR = 7.5 is kept smaller than that for NAR = 0. At the section of x/d = 20, the width of the contour plot of q_uv/U_e = 0.05 on the z axis is narrow compared with that of x/d = 5.

For NAR = 12.5, the contour plot at x/d = 5 shows a finite cruciform shape, and takes the maximum values at y/d = z/d ≅ ± 5.5 and the minimum values at y/d = z/d ≅ ± 4.0 on the y and z axes, respectively. The contour plot near the jet centre region shows the local minimum value because of the same reason as the case of NAR = 7.5. At the section of x/d = 30, the contour plot shows a cruciform shape with long axes in the y = ± z directions.

For NAR = 165, the contour plot shape along with the z axis at x/d = 5 shows the same tendency with another NAR cases. On the other hand, the contour plot along with the y axis shows a shape of quasi two-dimensional jet far from the jet centre region. The contour plot in the jet centre region shows a diamond-shaped because of the same reason as the cases of NAR = 7.5 and 12.5. At the section of x/d = 30, the width of the contour plot of q_uv/U_e = 0.05 on the z axis is narrower than that of the region of |y/d| ≤ 4.0.

From the results mentioned above, it is clarified that the development of the turbulent kinetic energy in the jet centre region for the cases of NAR ≤ .5 is suppressed compared with that for NAR = 0 due to the inward secondary flow velocity on both the y and z axes in the upstream region.

Turbulent velocity scales

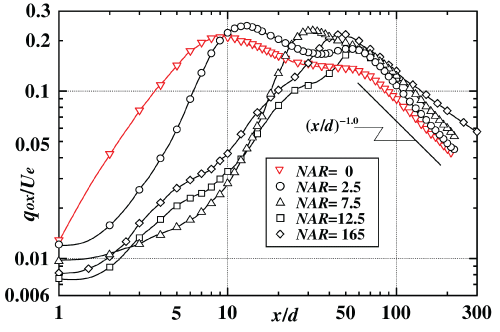
In this section, results of turbulent velocity scales in the upstream region will be focused, because it is presumed that the attachment of a rectangular notch, which promotes an inward secondary flow on the rectangular nozzle axis, makes a significant contribution to the development of the present turbulent flowfield in the upstream region. Figure 19 shows the streamwise variation of turbulent velocity scales q_ox/U_e along the x axis for all the NAR cases.

The values of the turbulent velocity scales for NAR ≥ 2.5 are suppressed in the region near the nozzle exit section (x/d ≤ 5) compared with that for NAR = 0. Furthermore, in the region of 5 ≤ x/d ≤ 20, the values of the velocity scale for NAR ≤ 7.5 are strongly suppressed compared with those for NAR = 0 and 2.5. Especially, in the region of 5 ≤ x/d ≤ 15, the value of the velocity scale for NAR = 7.5 and 12.5 are strongly suppressed. The reason of this suppression is explained as that the value of turbulent velocity scale q_ox/U_e is kept small because of the inward advection transport terms $\left(W\partial \left(U^2/2\right)/\partial z\right)$ on the y axis and ($W\partial \left(q^2/2\right)/\partial z$ on the z axis) due to the strong inward secondary flows on both the y and z axes, as shown in Figure 3, and the fluid lumps which are transported toward the jet centre region by these advection transport terms, have low turbulent level on both the y and z axes near the jet centre in the upstream region as shown in Figure 13.

From these results, it is found that the attachment of a rectangular notch perpendicular to the rectangular nozzle suppresses the development of turbulent velocity scale near the jet centre in the upstream region depending on the value of NAR.

Conclusions

The mean and turbulent flow fields of turbulent jet issuing from the rectangular nozzle with a rectangular notch at the midspan, have been investigated, experimentally. The object of this experiment is to investigate a possibility of the operation of the properties of both the mean and the turbulent velocity fields in the rectangular jet field by the attachment of a rectangular notch perpendicular to the rectangular jet. The results obtained are as follows:

1. The magnitude of the inward secondary flow velocity for NAR = 7.5 and 12.5 on the z axis in the upstream region, show the larger values compared with those of NAR = 0 and 2.5. Therefore, the magnitude of the inward secondary flow on the z axis can be operated by the value of NAR.

2. All PC length of the rectangular jet with a rectangular notch for NAR ≤ 2.5, take larger values compared with that of the rectangular jet (NAR = 0). This reason is explained as that there are the advection transports of mean kinetic energy $\left(W\partial \left(U^2/2\right)/\partial z\right)$ on the z axis and ($V\partial \left(U^2/2\right)/\partial y$ on the y axis) toward the jet centre region by the inward secondary flow velocity on both the z and y axes. Furthermore, the length of the PC region varies with the value of NAR and takes the longest one for NAR = 12.5. Therefore, the PC length of the rectangular jet with a rectangular notch can be operated by the variation of the value of NAR.

3. The half velocity width b_z/d on the z axis for all NAR takes each minimum value due to the inward secondary flow in the upstream region and the b_z/d for NAR = 165 takes the minimum value. Therefore, the development of the half velocity width b_z/d on the z axis can be operated by the variation of the value of NAR.

4. The attachment of a rectangular notch perpendicular to the rectangular nozzle suppresses the development of turbulent velocity scales near the jet centre in the upstream region depending on the value of NAR due to the inward secondary flow velocity on both the y and z axes.

References

1. Lilley GM (1984) Aerodynamic noise - A review of the contributions to jet noise research at the College of Aeronautics, Canfield 1949-1961 (together with some recent conclusions). Aeronautical Journal 88: 213-223.
2. Bevilaqua PM (1974) Evaluation of hyper mixing for thrust augmenting ejectors. Journal of Aircraft 11: 348-354.
3. Yu S (2003) Japanese patent disclosure 2003-268523 (in Japanese).
4. Trentacoste N, Sforza PM (1967) Further experimental results for three-dimensional free jets. AIAA Journal 5: 885-891.
5. Sforza PM, Stasi W (1979) Heated three-dimensional turbulent jets. J Heat Transfer 101: 353-358.
6. Krothapalli A, Baganoff D, Karamcheti K (1981) On the mixing of a rectangular jet. Journal of Fluid Mechanics 107: 201-220.
7. Quinn WR (1992) Turbulent free jet flows issuing from sharp-edged rectangular slots: The influence of slot aspect ratio. Experimental Thermal and Fluid Science 5: 203-215.
8. Marsters GF, Fotheringham J (1980) The influence of aspect ratio on incompressible turbulent flows from rectangular slots. Aeronautical Quarterly 31: 285-305.
9. Fujita S, Osaka H (1992) Effect of aspect ratio on potential core length for cruciform jet. Experimental Thermal and Fluid Science 5: 332-337.
10. Fujita S, Harima T, Osaka H (2009) Turbulent jets issuing from rectangular nozzles with a rectangular notch at the midspan. Fluid Structure Interaction V 105: 61-70.
11. Quinn WR, Marsters GF (1985) Upstream influence on turbulent jet flows from cruciform nozzles. Aeronautical Journal 89: 55-58.
12. Quinn WR, Militzer J (1988) Experimental and numerical study of a turbulent free square jet. Physics of Fluids 31: 1017-1025.
13. Quinn W (1989) On mixing in an elliptic turbulent free jet. Physics of Fluids 1: 1716-1722.
14. Fujita S, Harima T, Osaka H (1999) Turbulent jet issuing from a quasi two-dimensional nozzle with a rectangular notch at the midspan (streamwise variation of mean velocity field). Transactions of the Japan Society of Mechanical Engineers, Series B 65: 905-911.
15. Zeng Y, New TH, Tsai HM (2009) On the notched collars on an axisymmetric jet. Experimental Thermal and Fluid Science 33: 1029-1034.
16. New TH, Tsovolos D (2013) On the vortex structure and behavior of notched elliptic jets. Experimental Thermal and Fluid Science 49: 51-66.
17. Sfeir AA (1979) Investigation of three-dimensional turbulent rectangular jets. AIAA Journal 17: 1055-1060.