Annals of Atoms and Molecules

Excitations of the B¹Δ, C¹П, and D¹∑⁺ States of N₂O Molecule by Positron Impact

Abstract

We report cross-sections for excitations of the B¹Δ, C¹Π, and D¹∑⁺ states of N₂O molecule by positron impact using the scaling Born positron (SBP) method [J LS Lino, Chin. J. Phys. 54 223(2016)]. The SBP method is applicable only to dipole-allowed excitations and to our knowledge, up to date no experimental data and theoretical results are available for comparison. Similarities and differences with electron-N₂O scattering case are discussed. A study to check convergence characteristics using the annihilation parameter Z_eff (classical Z) is tested.

PACS: 34.80.Dp

Keywords

Born, Positron, Scaling

Introduction

Fundamental uses of positrons include the formation of neutral antihydrogen atoms, astrophysics process, phenomena including plasmas, molecular clusters and nanoparticles. Many, if not most, of these uses of positrons depend on a quantitative understanding of the basic interactions of positron with molecules [1]. Several processes are of interest and include, for example, electronic excitation, positronium formation, polarization, multichannel effects, and ionization. In our atmosphere, nitrogen oxides are generated as a product of the combustion of fossil fuels and N₂O is known to be generated in selective catalytic reduction reactions and is a known cause of global warning. The N₂O molecule is considered one of the major air pollutants in Earth´s atmosphere [2]. In particularly, N₂O is a linear triatomic molecule with a small permanent dipole and represent a strong challenge for the study of positron as incident particle. From the theoretical point of view, we note that work on positron-N₂O scattering are very scarce when compared with electron scattering case. For example, Arretche, et al. [3] reported elastic cross-sections for positron-N₂O scattering using the Schwinger multichannel method (SMC). Baluja and Jain reported (elastic+inelastic) cross-sections using the parameter-free model potential [4]. On the experimental side relative differential cross-sections for quasielastic including rotational and vibrational excitations positron-N₂O scattering in the 4-100 eV range were measured and reported by Przybyla, et al. [5]. Still on the experimental side, Kwan, et al. [6] reported total cross sections for positron-N₂O scattering in the 1-500 eV incident energy range. Studies on the theoretical side and experimental data including positron-N₂O scattering are widely discussed by Surko, et al. [7].

We recently reported electronic excitation cross sections for positron-CO [8], N₂ [8], NO [8] and C₆H₆ [9] scattering using the called scaled Born positron method [8,9]. The results obtained for these molecules using the SBP method are in excellent agreement when compared with sophisticate methods which suggest that the SBP method can be a reliable tool for the study of positron-molecule scattering. Motivated by these results using the SBP method we will investigated the electronic excitation by positron impact of N₂O molecule considering the B¹Δ, C¹Π, and D¹∑⁺ states. As far as we know, this is the first time that inelastic cross-sections are reports for N₂O molecule using the SBP method and a comparison of our cross-sections with electron-N₂O scattering case are necessary and can provide a interesting insight on differences and similarity of e± - N₂O scattering. In the present study the positronium formation channel is not considered.

In Sec.2 we will identify the SBP method for investigated cross sections for the B¹Δ, C¹Π, and D¹∑⁺ states of N₂O molecule. In Sec.3 computational procedures and results are discussed. Conclusions are presented in Sec.4.

Theory

Recently, Lino proposed [9] the scaled Born positron (SBP) based on the original scaling plane wave Born for electron-molecule collision [10]. The SBP method was found to convert the traditional first Born approximation integral cross sections to reliable cross-sections when compared with sophisticate methods. The traditional first Born approximation (FBA) is used here as the main step, i.e, the plane wave is the correct function at infinity. The FBA can be written as

$${\sigma }_{Born}=\left[\left(4\pi a_o^{2}R\right)/E\right]f_{FBA}\text{ (1)}$$

The SBP method represent a optimization of Eq.(1), i.e., the SBP method replaces the E (energy) that appears in the denominator of Eq.(1) by E + (E_exc + E_Ps ). The Eq.(1) can be rewritten as

$${\sigma }_{SBP}=\left(f_{accur}/f_{Born}\right).f\left(E\right).{\sigma }_{Born}\text{ (2)}$$

where

$$f\left(E\right)=\left[\left(\frac{E}{E+\left(Eps+Eex\right)}\right)\right]\text{ (3)}$$

The Eq. (2) has some important aspects. First, E_ps is the positronium energy of the target and is used only when the incident particle is the positron which is not identical to the target electrons. Second, Eexc is the excitation energy, f_accur is an accurate dipole value from experiments or from accurate wave functions, and f_Born is the dipole value from the traditional FBA and these parameters are free of adjustable. Third, the constant (E_Ps + E_ex) has some consequences practical to the performance of the SBP method [8,9]. For example, the constant is related with energy of the incident positron in the field of the nucleus and the bound electrons of the target. The Eq. (3) also can be seen as the scaling factor to represent the correlation between the positron and electrons of the target. Furthermore, the "scaling factor" here proposed suggests a similarity with polarization effects [9]. The positronium (Ps) energy used in the eq. (3) is written as

$$E_{ps}=B-6.8eV\text{ (4)}$$

where B is the binding energy of the electron of target. Finally, the f (E) factor reduces the FBA at low energies while keeping the validity of the Born approximation at high energies and the SBP method has the effect of correcting the FBA.

Computational Aspects and Results

Following Arretche, et al. [3] the experimental equilibrium geometry of the ground state R_(N-N) = 2.127 ao and R_(N-O) = 2.242 a_o is here used. The basis set used (9s5p/4s3p) is the same investigated by Arretche, et al. [3] using the SMC method for elastic positron-N₂O scattering [3]. This basis set given a ground state value of -183.727 a.u and a dipole moment of 0.6531D computed using the GAMESS code as in Ref. [3]. Table 1 shows vertical excitation energies compared to experimental data. The appropriated f_accur(f_Born) values to use in the SBP method were deduced from the GOS [10] and the positronium enegy value is 6.1 eV.

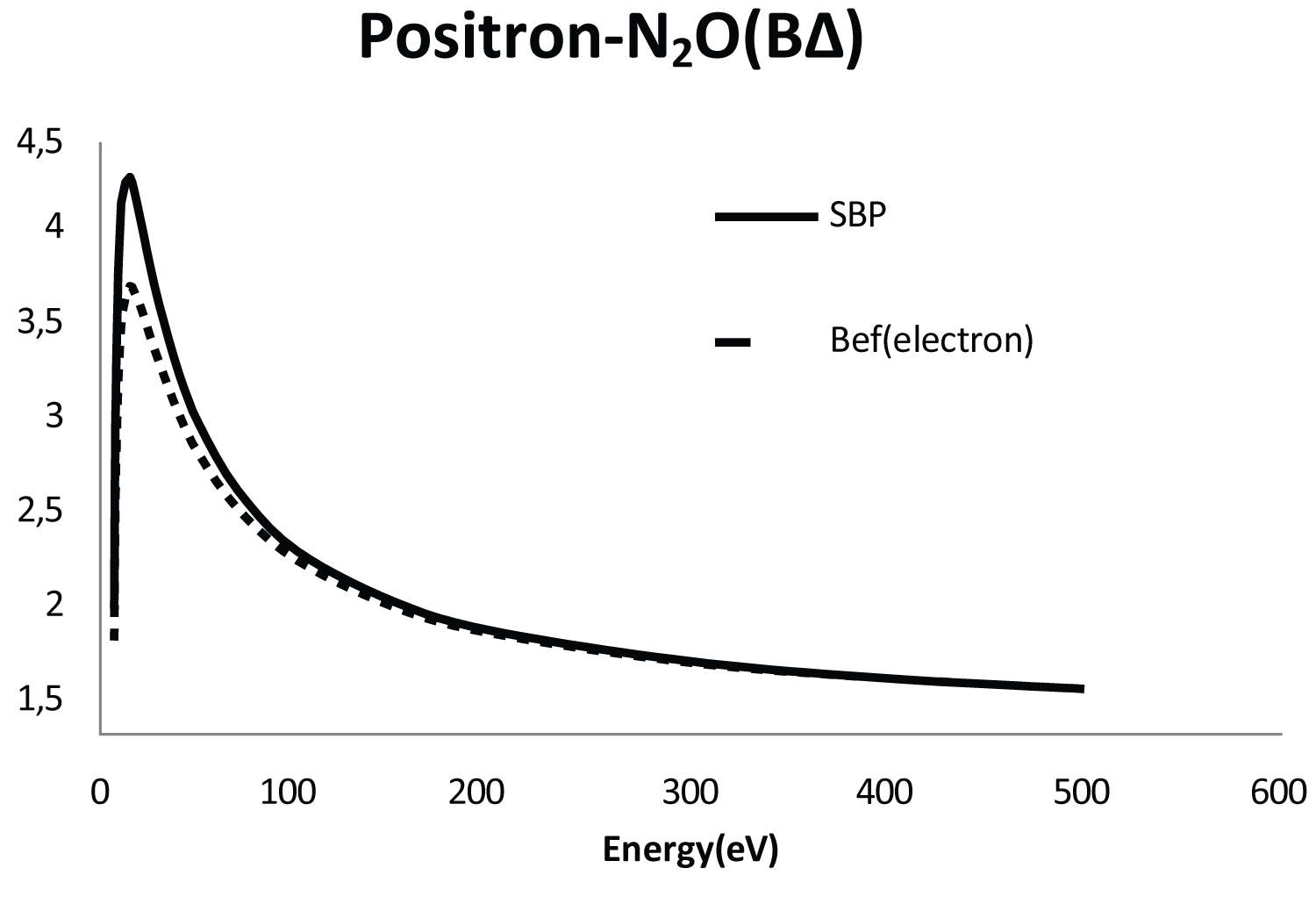
In Figure 1 we report cross sections for the B¹Δ state using the SBP method. Also included in Figure 1, for purposes of comparison only, the called BEf-method for electron scattering case. As observed in Figure 1, at low energies the cross-section for positron scattering is larger when compared with electron case using the BEf-method. Is interesting to point out that a similar behavior between the cross sections can be observed, i.e., the SBP method not only increase the cross sections magnitude at low energies but also shifts the peak to higher energy. As observed also in Figure 1 at higher energies cross sections for positrons and electrons are very similar. As a first analysis Figure 1 shows a behavior expected.

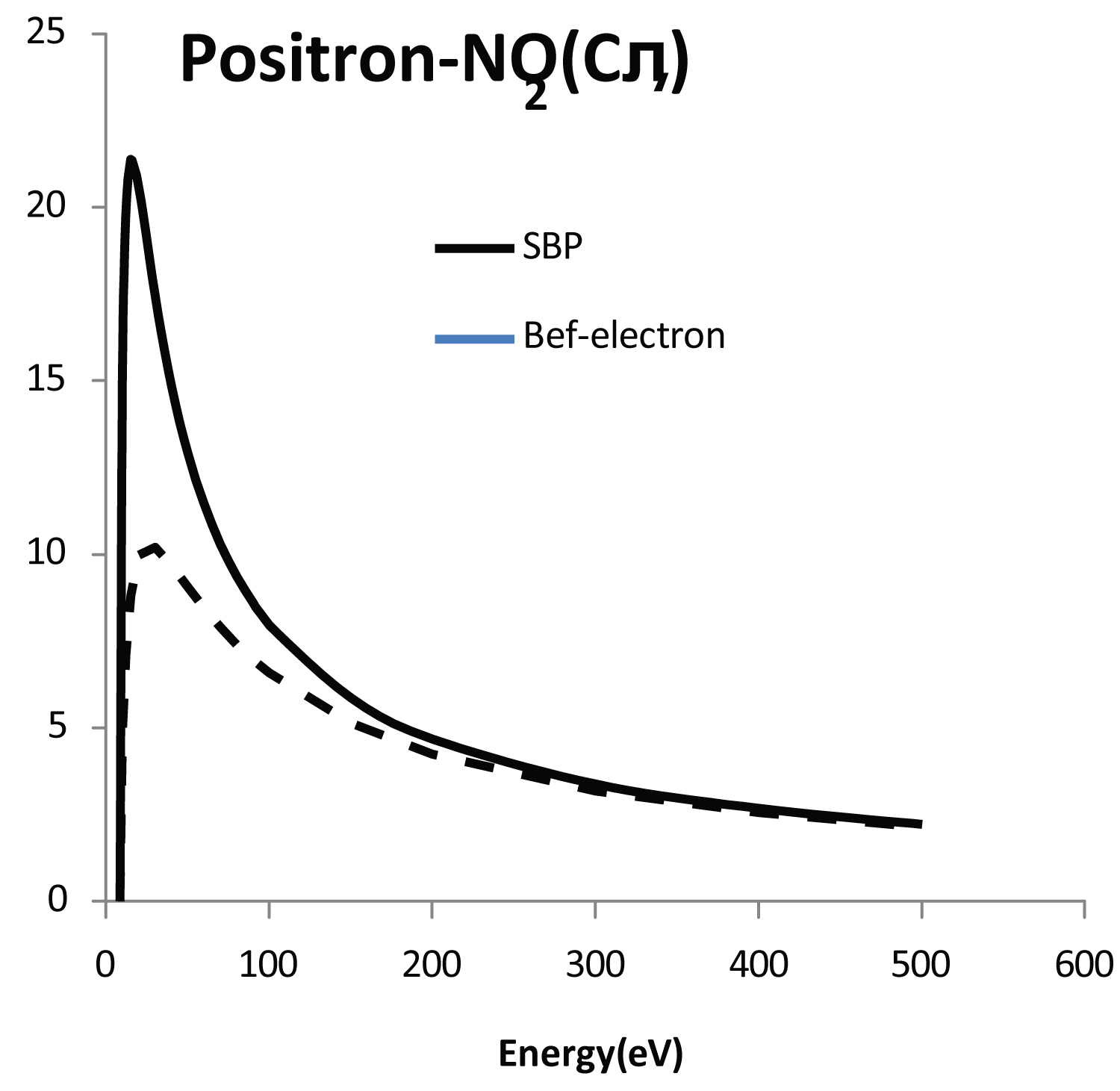
In Figure 2 we report integral cross-sections for the C¹π state using the SBP method. For clarity our results, we choose to compare again the BEf-method [11] used for electron- N₂O scattering. This scenario is specially important since it can define the quality and validity of the FBA used (BEf-method also close for FBA at higher energies) and as observed at low energies the SBP cross sections is larger when compared with electron case. Examination of Figure 1 and Figure 2 indicates that, cross sections for the B¹Δ, and C¹Π states are very different in magnitude but with shape similar. As cited in Figure 1 at higher energies cross sections for positrons and electrons are also very similar.

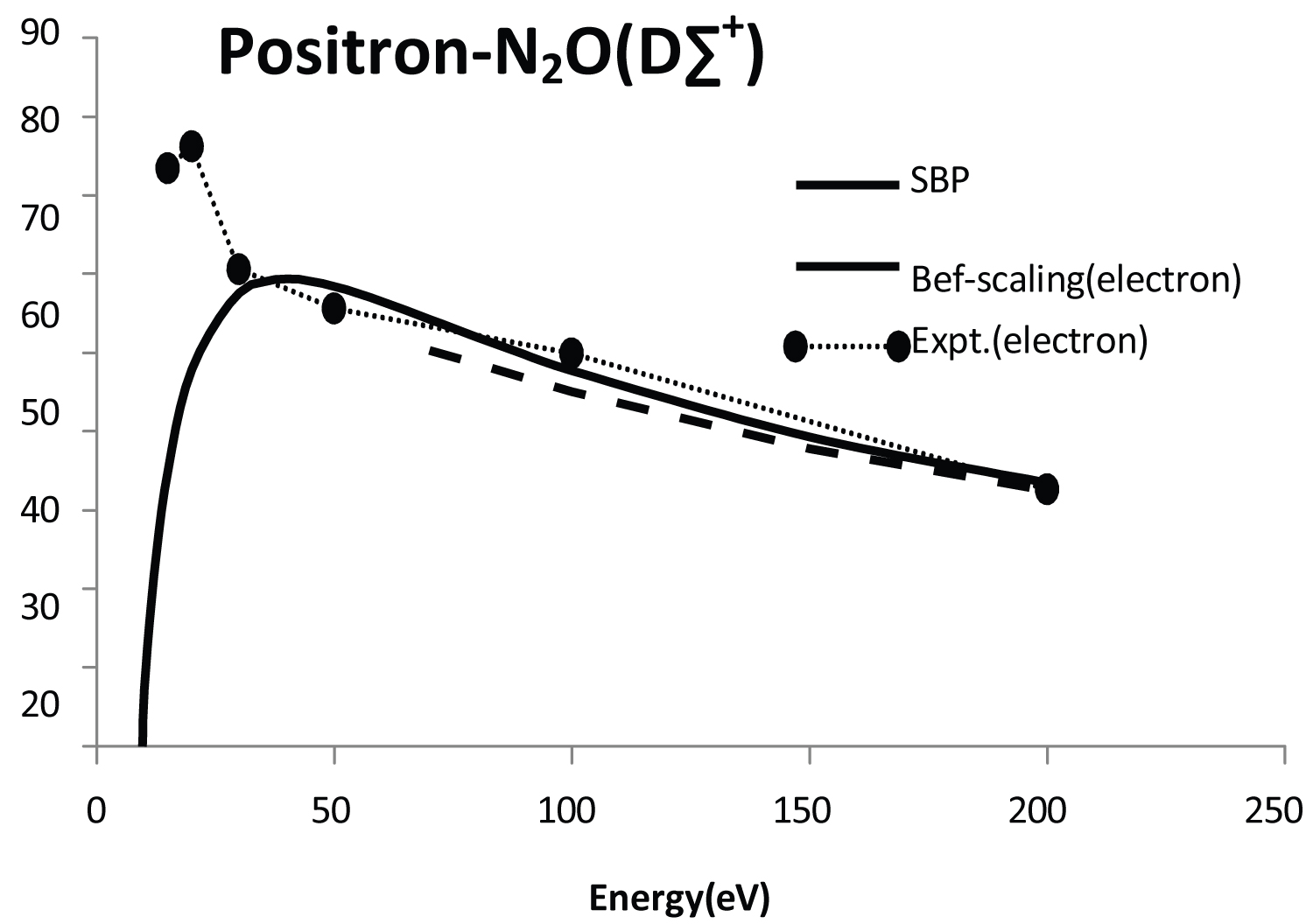
In Figure 3 we report cross sections for the C1π state and in the absence of experimental data the SBP method is compared with experimental data for electron case and again the BEf-method [11]. First, at low energies the SBP method shows cross sections with different magnitude when compared with experimental data for electron case. In fact, is seem from this figure that there is a significant difference between the SBP method and experimental data for electron scattering case at low energies (is expect that the positron inelastic cross-section to be larger in magnitude than the corresponding electron inelastic cross-section). It is interesting to point that a similar behavior was observed by Arretche, et al. [3] for the elastic positron-N₂O scattering cross-section and reason for this behavior remains as a problem to be better understood. The present study suggests that further development of the current scattering models is needed.

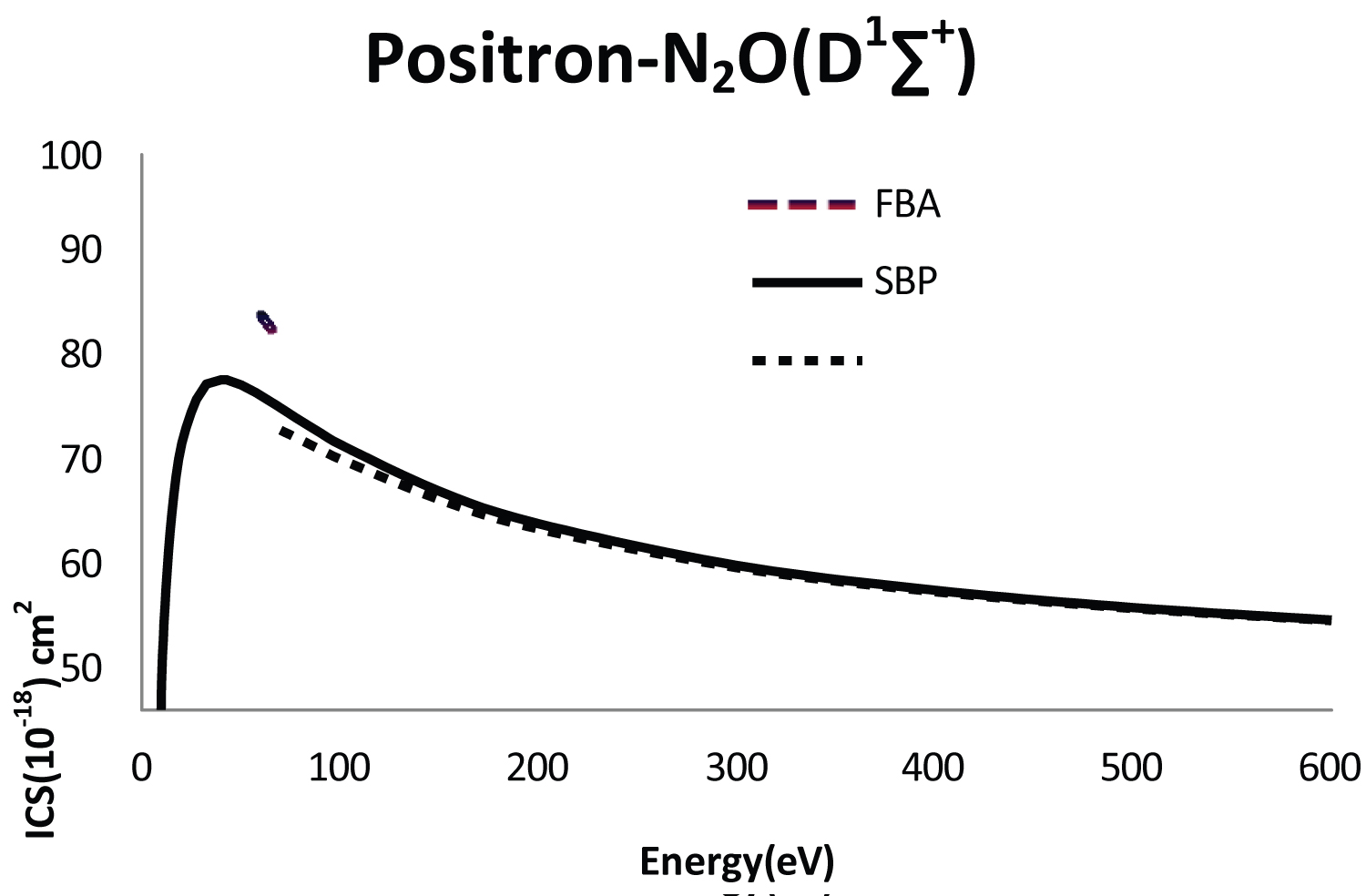
In Figure 4 were port integral cross-sections for the 1D∑+ state using the SBP method now in the10-600 eV incident energy range. The results are compared with the BEf-method [11] and the traditional FBA. As observed in Figure 4 the SBP method and BEf method closed with the FBA at higher energies (as expected). The good agreement with the FBA at higher energies is the aspect that basically determines the level of numerical convergence.

In the Table 2 integral crosssections for B¹Δ, C1π, and D¹∑⁺ electronic state using the SBP method are listed for future reference.

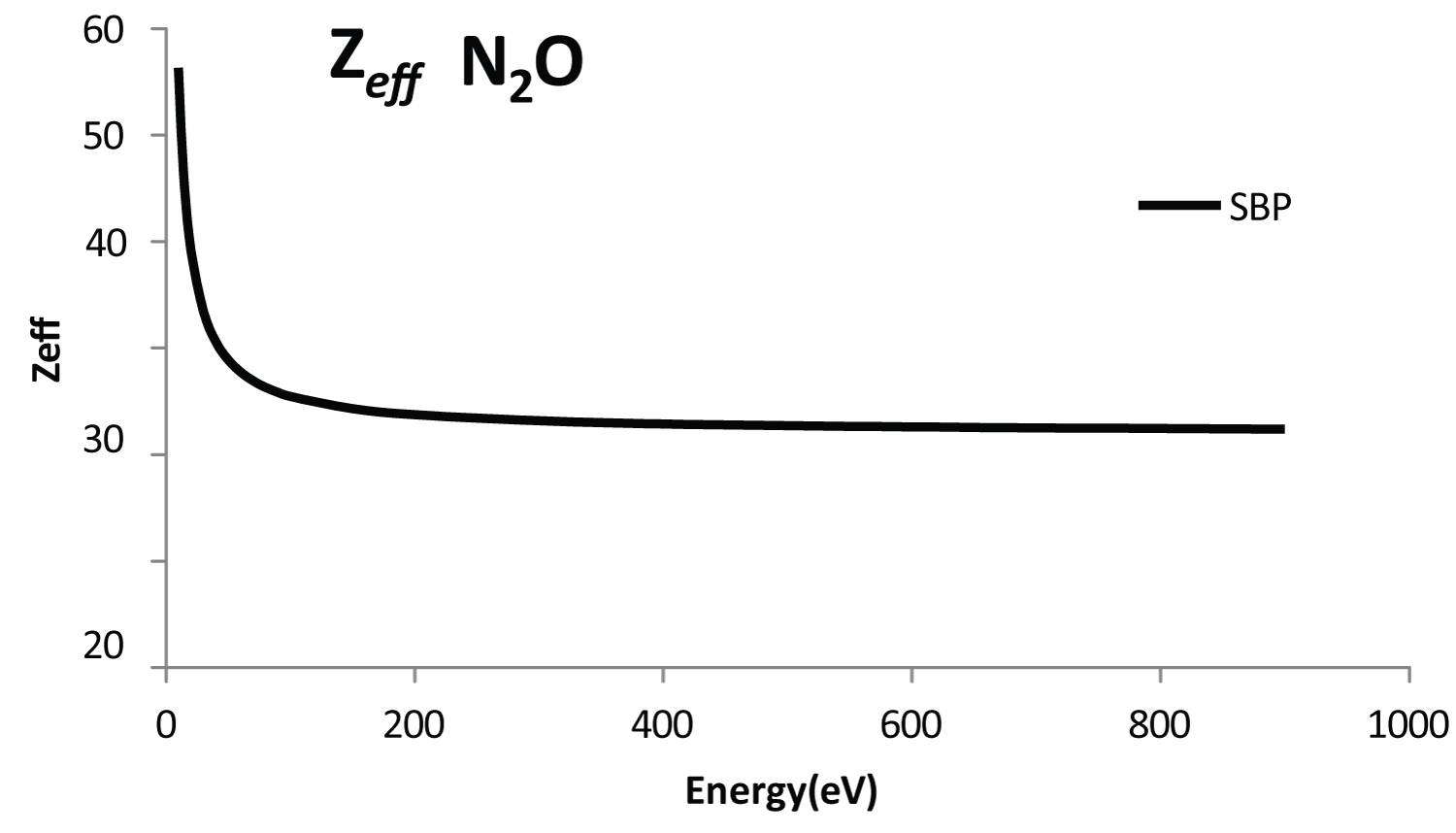
Finally, a convenient way of dealing also with convergence aspects of SBP method is the analysis of the annihilation Z_eff parameter classical, which is traditionally written as

$$Z_{eff}={{\displaystyle \int \sum }}_{i=1}^z\delta \left(r-r_i\right)\left|\psi \left(r_1,\mathrm{.....},r_z,r\right)\right.\left|{}^{2}d\right.r_1\mathrm{...}d{r}_z,dr\text{ (5)}$$

The Eq.(5) represent the effective number of electrons that contribute to the annihilation process, and ψ(r₁,...,r_z,r) is the total wave function of the Z electron and one positron coordenates [7]. If substitutes the asymptotic, plane wave function into equation (5), one obtains Z_eff = Z. We have noted that the SBP method can determine the Z_eff = Z classical based on the Born approximation, i.e., the Z_eff^(SBP) represent also a criteria to check the quality of SBP method. The accuracy of the Z_eff Born approximation can be given by eq(6) (Figure 5)

$$Z_{eff}^{\left(SBP\right)}=\left[\left({\sigma }_{Born}/{\sigma }_{SBP}\right)\right].Z\text{ (6)}$$

Conclusion

We have discussed a recently developed method for investigate inelastic positron-target scattering. The scaled Born positron (SBP) method improved was tested to electronic excitation of N₂O (B¹Δ, C¹π, and D¹∑⁺ state) with cross sections substantially, in principle, adequate when compared with electron case (as far as we know, this is the first time that cross-sections are reported using the SBP method). Calculated cross-sections using the SBP method agree well with electron case at higher energies. On the other hand, the not expected behavior between our results and experimental data at small energies when of electron incident still remains as a problem to be better understood (similar effect may be observed also in the elastic case). In order to check the numerical convergence of the SBP method the Z_eff classical (Z parameter) was appropriately obtained, giving confidence that the SBP method is significant for positron-N₂O scattering. As observed the literature for inelastic positron-N₂O molecule is less clear, and however new results are welcome.

References

1. Fojon OA, Rivarola RD, Hanssen J, et al. (2001) Positronium formation in positron-simple metal cluster collisions. J Phys B 34: 4279.
2. Nahar SN, Antony B (2020) Positron scattering from atoms and molecules. Atoms 8: 29.
3. Arretche F, Mazon KT, Michelin SE, et al. (2008) Low-energy elastic scattering of positrons by N₂O. Phys Rev A 77: 042708.
4. Baluja KL, Jain A (1992) Total (elastic and inelastic) scattering cross sections for several positron-molecule systems at 10-5000eV. Phys Rev A 45: 7838.
5. Przybyla DA, Addo Asah W, Kauppila WE, et al. (1999) Measurements of differential cross-sections for positron scattered from N₂, CO, O2, N₂O, and CO2. Phys Rev A 60: 359.
6. Kwan K, Hsier YF, Kauppila WE, et al. (1984) Total scattering measurements and comparisons for collisions of electrons and positrons with N₂O. Phys Rev Lett 52: 1417.
7. Surko CM, Gribakin GF, Buckman J (2005) Low-energy positron interactions with atoms and molecules. J Phys B 38: R57.
8. Lino JLS (2022) Some aspects and progress in the description of the scaling born positron approach. J Mol Phys 2: 14.
9. Lino JLS (2021) Electronic excitation of C₆H₆ by positron impact. Rev Mex Fisica 67: 188.
10. Vindokumar M, Barot M (2012) Scattering of N₂O on electron impact over an extensive energy range (0.1eV–2000eV). J Chem Phys 137: 074311.
11. Tanaka H, Brunger MJ, Campbell L, et al. (2016) Scaled plane-wave Born cross sections for atoms and molecules. Rev Modern Phys 88.