Positron-Hydrogen Atom Scattering, Excitations, and Positronium Formation Using the Scaled Born Positron Method

Abstract

We report here cross sections for excitations of 1S-2 ¹ S, and 1S-nP states ( n = 2,3,4,5,6) of hydrogen atom by positron impact using the scaled Born positron (SBP) method [J.L.S.Lino, Inter. J. At. Nucl. Phys.7 028 (2023)]. Particular attention is paid to the positronium formation channel which for the first time, integral cross sections are investigated using the SBP method. The present results for excitation to the higher levels are believed to the only data available (using SBP method) and illustrate the good convergence characteristics of the procedure.

Keywords

Born, Positron, Scaling

PACS: 34.80.Dp

Introduction

Fundamental uses of positrons include the formation of neutral anti hydrogen atoms, and new ways to study a wide range of phenomena including plasmas, atomic clusters and nanoparticles [1]. Many, if not most, of these uses of positrons depend on a quantitative understanding of the basic interactions of positron with matter [1]. Several processes are of interest and include electronic excitation, positronium formation, and also ionization. For years positron-hydrogen atom scattering has been an important prototype of studies to both theoreticians and experimentalists [1]. A series of experiments involving positron-H atom scattering has been done [2] (positron can be obtained from radioisotopes or electron-positron pair production) so that the theoretical calculations still are extremely important for an adequate comparison. For example, sophisticate methods used to investigate positron-H atom scattering (excitations, ionization, and positronium formation) as the close coupling approximation (CCA) [3], Kohn variational principle (KVP) [4], Fadeev equations [5], polarized orbital’s of Temkin [6], and others first-principle calculations were also published [7]. With the advance of quantum mechanical computational methods very accurate Ab initio methods were established but these calculations are very time consuming, limiting the domain of applicability of such models for some targets. As an alternative many analytical formulas have been developed to overcome these difficulties and the merit of analytical expressions is of convenience and increased applicability when cross sections may be required in more complicate modeling situations [8].

As well knowledge, a simple and computational fast way to calculate positron (electron) collisional excitation cross sections for atoms is by using the first born approximation (FBA) [9]. This is essentially a high-energy approximation and when collisional excitation rates are sensitive to values of the cross sections near threshold, the approximation of these rates can be poor. However, the FBA calculated from simple wave functions serve as adequate starting points. When dealing with dipole allowed transition, the long-range character of the dipolar coupling requires a larger number of partial waves and the FBA, in principle, can be used to include these contributions [10]. First calculations of positron-H scattering have been performed by Massey and Mousa using the FBA [10] for investigate inelastic cross sections and since then, others studies using the FBA for positronium formation, and ionization process can be obtained in Refs [11-13]. Ab initio methods, in principle, involve such large basis set, complicated coupled equations, and integrations out to large distances that they are not easily applied to each atom (or molecule) for which data are needed.

The motivation of present work is to study the inelastic positron-H atom using the conceptually simple scaled born positron (SBP) method [14,15] and we will verify that the SBP has the capability to produce accurate integral cross sections (ICS) when compared with sophisticates methods. In particular the SBP method has as point start the FBA and we will see that the SBP is able to describe positron-atom scattering (subsequent papers using the SBP show equally good results for H ₂ [14], and C ₆ H ₆ [15] targets) and our study using hydrogen atom as target would be of considerable interest for further experimental work.

In Sec 2 we will identify the SBP method for investigated the positron-H atom scattering in particular the 1s-2 ¹ S, 1s- n P states ( n = 2,3,4,5,6), and positronium formation. In Sec.3 computational procedures and results are discussed. Conclusions are presented in Sec.4.

Theory

The FBA is used here as the starting point, i.e., the plane wave is the correct function at infinity for an positron-atom scattering. The SBP method proposed here apply only to integrated excitation cross sections and is applicable only to dipole-allowed excitations. In a generic form the FBA can be written as

$${\sigma }_{Born}=\left[\left(4\pi {\text{a}}_o^{2}R\right)\text{/E}\right]f_{FBA}\text{ (1)}$$

The SBP method replaces the E (energy) that appears in the denominator of Eq.(1) by E + (E _exc + E _Ps ) and Eq.(1) is rewritten as

$${\sigma }_{SBP}=\left(f_{accur}/f_{Born}\right).f\left(E\right).{\sigma }_{Born}\text{ (2)}$$

Where

$$f\left(E\right)\text{ = }\left[\left(\frac{E}{E+\left(Eps+Eex\right)}\right)\right]\text{ (3)}$$

E _ps is the positronium energy, E _exc is the excitation energy, E is the energy incident of positron particle, f _accur is an accurate dipole value from experiments or from accurate wave functions, and f _Born is the dipole value from first born approximation (FBA). As observed in Eq.(3), E is increased by a constant (E _Ps + E _ex ) and this modification has some consequences practical to the performance of the SBP method [14-16]. The constant is related with energy of the incident positron in the field of the nucleus and the bound electrons of the target and the Eq.(3) can be seen as the scaling factor to represent the correlation between the positron and electrons of the target. It may be observed that cross sections obtained using the FBA are identical for electron and positron as projectiles but the f (E) factor identify, for example, the incident positron. The positronium (Ps) energy used in the eq.(3) is written as

$$E_{ps}=B-6.8eV\text{ (4)}$$

where B is the binding energy of the electron of target. The f (E) factor reduces the FBA at low energies while keeping the validity of the born approximation at high energies and the SBP method has the effect of correcting the FBA (when dealing with dipole transitions the long-range character of the dipolar coupling requires a larger number of partial waves and because of it, higher partial waves are not well described for several sophisticates ab initio methods). This consideration is especially important, i.e., in the practical such an effort can be avoided if above a certain angular momentum the remaining partial waves, which are weakly scattered, are obtained from a weak collision theory such as the FBA [16]. As we will see, in principle, the SBP method can generate cross sections reliably and quickly when compared with others methods and experimental data. Important mentioned that integral cross sections using the SBP method are reported and compared, in details, with selected sophisticates methods.

Computational Procedures and Results

Excitation to the n S, and n P states

We have used Hartree-Fock calculations to represent the ground state of the target with the same basis set used (Cartesian Gaussian) in Ref [3]. With this basis set we have obtained excitations energies listed in Table 1 and Table 2. The positronium energy (E _ps ) is 6.8 eV. Table 3 show integral cross sections for e ⁺ -H atom (1s-nP) using the SBP method.

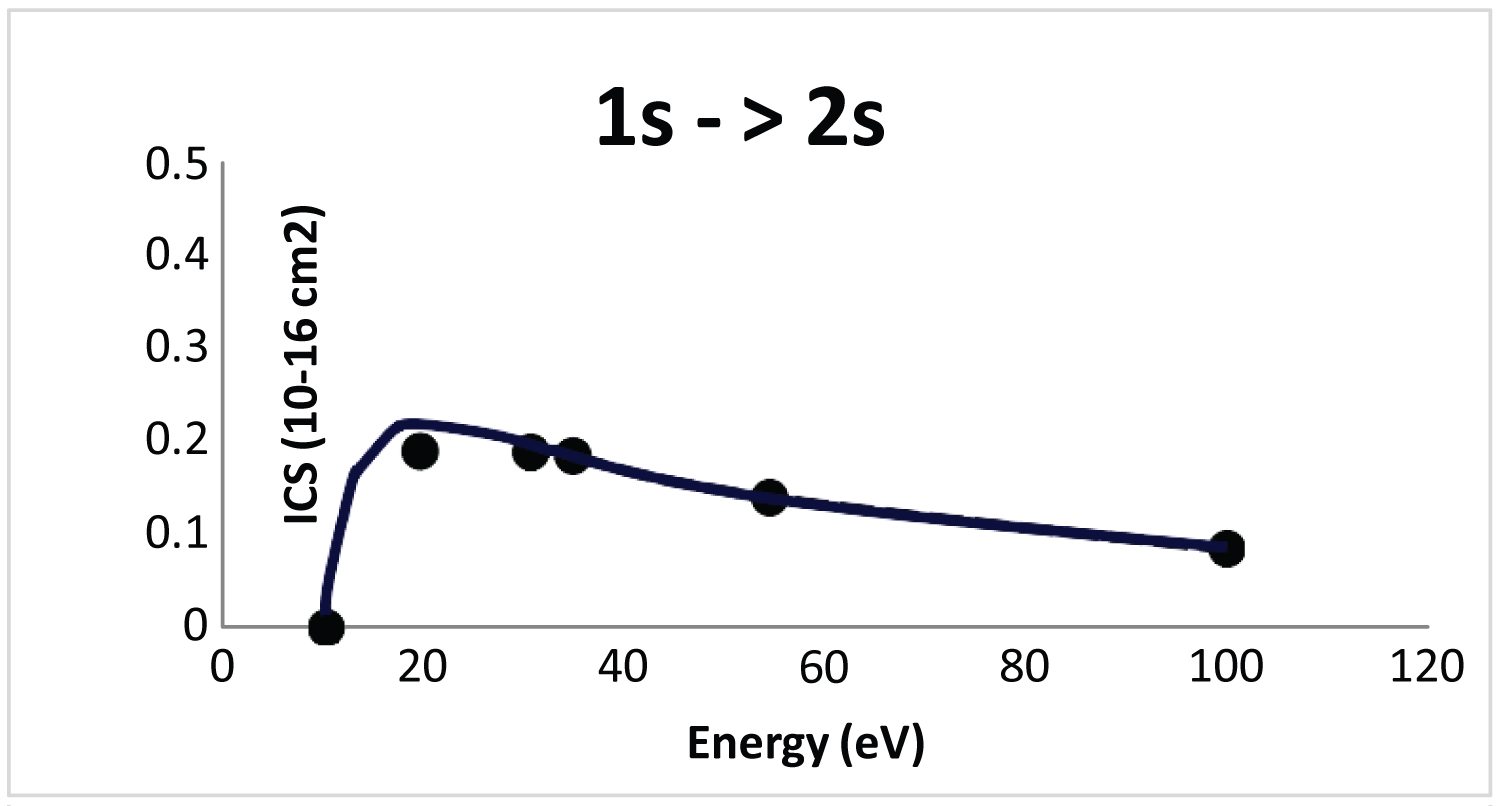
For a quantitative study, we will compare the SBP method with sophisticate’s methods. Evidently numerous methods can be obtained in the literature for e ⁺ - H atom system, but here we will discuss as the SBP method can be accuracy (or not) when compared with a unique sophisticate and appropriate method. In Figure 1 we show integral cross section for the 1s → 2 ¹ s electronic transition using the SBP method compared with the FBA traditional, only. As observed the SBP method not only reduces the cross sections magnitude at low energies, but also shifts the peak to a higher “E” vality of the FBA intact. As expected the SBP converge to the FBA at high energies.

In Figure 2 we show integral cross section again for the 1s → 2s electronic transition where the SBP method is compared now with the traditional distorted wave approximation (DWA) [17]. As observed our SBP method and DWA are very similar in magnitude and is important discuss some points. First, the FBA transition amplitude for the direct process 1s-2s is small and Figure 2 clearly demonstrates the utility of the SBP method when compared with the sophisticate DWA [17]. Second, the DWA [17] is able to perform calculations for positron-atom scattering but the method can considerably enlarge the computational effort. This same computational effort is obviously not found in the SBP method.

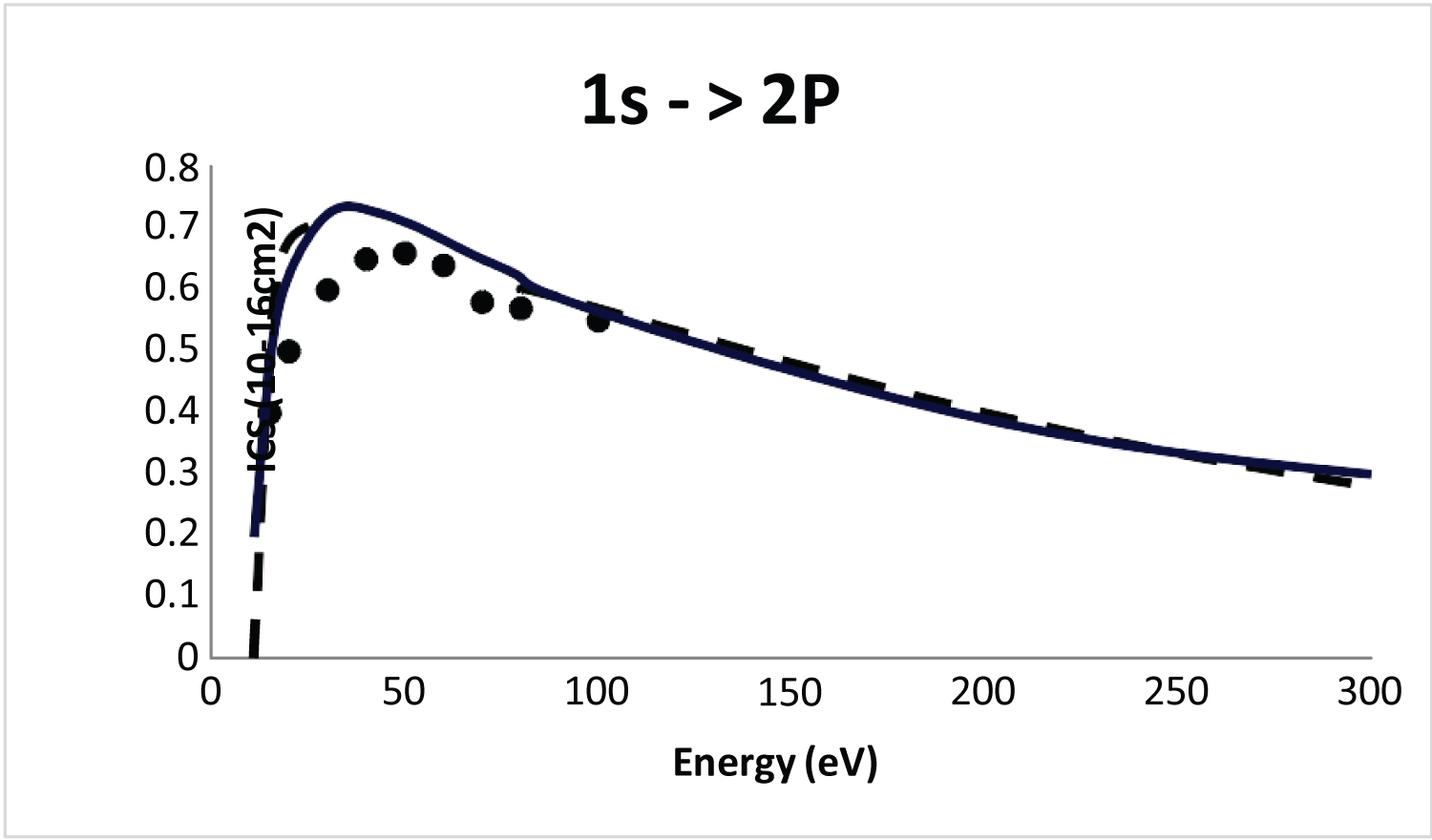
In Figure 3 we show the SBP integral cross section for the 1s → 2p electronic transition compared now with two methods, the relevant DWA [17] and the able convergent close coupling (CCC) [18] method for the electron case. Note that as in Figure 2, the cross-sections using the SBP method provide a good convergence with the able DWA [17], giving confidence that our SBP method is consistent. Also as expected, Figure 3 shows the SBP, and DWA [17] closed with the CCC method (electron case) [18] at higher energies (the corresponding excitation cross-sections by electron impact is similar but smaller).

As observed the Figure 1, Figure 2, and Figure 3 showed that the SBP method is very similar with the traditional and able DWA method [17] which produce highly accurate results, though they require orders of magnitude more computational effort than SBP cross-sections.

Positronium formation (Ps)

The inclusion of Ps-formation is crucial in situations such as positron scattering by atoms, molecules and also positron scattering from alkali-metal atoms, where the Ps-formation channel is open at all energies. Rigorous treatment of this process is difficult, especially for many-electron targets. This remains one of the most significant challenges for positron scattering theory. Here we will study the Ps formation in the SBP context. In our model using the FBA, the reaction

$$e^{+}\to H\left(1s\right)\to Ps\left(1s\right)+proton\text{ (5)}$$

represent a three-body problem, or arrangement process in which an electron from a bound orbital centered on the proton to a bound orbital around the moving positron. The FBA for Ps-formation provides analytical expressions very similar to Ref [11] and additional details using the SBP method can be found in Ref [19,20]. Hence, we present no details here, but a few working expressions for the sake of completeness. The integral cross section using the SBP method is given by

$${\sigma }_{SBP}=\left(f_{accur}/f_{Born}\right).\left[\left(\frac{E}{E+Eps}\right)\right].{\sigma }^{Ps}\text{ (6)}$$

where now σ ^Ps represent the integral cross sections using the FBA for positronium formation [19]. Experimental determination of the cross-section of positronium formation in hydrogen atom can be obtained in Ref [2]. Table 4 shows integral cross-sections for positroniumm formation using FBA, SBP method, CCC [18], and experimental data [2]. If we are not so rigorous, we can see in Table 4 a reasonable agreement between our SBP method and the CCC method [18] and this comparison is very important, i.e., the CCC method [18] is able to perform calculations for positron-atom scattering but the CCC method can considerably enlarge the computational effort. This same computational effort is obviously not found in the SBP case. Also can be observed good agreement between the SBP method and experimental data [2]. These results suggest that the SBP method is consistent.

Conclusion

We have discussed a study on the scaled born positron (SBP) method for positron-H atom collision. The present paper has examined the validity of the SBP method to calculating integral cross sections for 1S-2 ¹ S, and 1S-nP ( n = 2,3,4,5,6) states of H atom by positron impact. Analysis of the results indicated that the SBP is significant, with good convergence characteristics when compared with sophisticate’s methods. In particular the positronium formation using the SBP method shown cross-sections with great similarity with sophisticate methods indicant a good performance of the scaled born positron.

References

1. Stein TS, Harte M, Jiang J, et al. (1998) Measurements of positron scattering by hydrogen, alkali metal, and other atoms. Nuclear Instruments and Methods in Physics Research Section B 143: 68-80.
2. Surko CM, Gribakin GF, Buckman SJ (2005) Low-energy positron interactions with atoms and molecules. J Phys B 38: R57.
3. Mitroy J (1995) Large basis calculation of positron-hydrogen scattering at low energies. Aust J Phys 48: 645-675.
4. Fabrikant II, Gribakin GF (2014) Similarity between positronium-atom and electron- atom scattering. Phys Rev Lett 112: 243201.
5. Mngoue MS, Denabe A (2020) Positron-impact single ionization of helium using the faddev equations. Phy Scr 95: 045401.
6. Bhatia AK, Temkin A, Drachman RJ, et al. (1971) Generalized hylleraas calculation of positron-hydrogen scattering. Phys Rev A 3: 1328.
7. Lino JLS, Germano JSE, Lima MAP (1994) Electronic excitation of H2 by positron impact: An application of the Schwinger multichannel method. J Phys 27: 1881-1888.
8. Burkova LA, Ochkur VI (1979) Calculations of inelastic electron scattering from atoms in the second born approximation.
9. Karwasz GP (2015) Positrons - an alternative probe to electron scattering. Eur Phys J D 35: 267-278.
10. Lino JLS (2015) 17th Int. Conf. Positron Annihilation-17, China, Abstract.
11. Lugosi L, Gyemant IK (2014) A simple model for positronium formation in positron-hydrogen atom collisions. Heavy Ion Phys 13: 267-275.
12. Kulhar VS (2008) Positronium formation in 2S-state in atomic hydrogen. Indian Journal of Pure & Applied Physics 46: 245-250.
13. Ivanov IA, Mitroy J (2000) Optical model theory for positron annihilation during Scattering. J Phys B 33: L831-L837.
14. Lino JLS (2022) Some aspects and progress in the description of the scaling born positron approach. J Mol Phys 2: 14-18.
15. Lino JLS (2021) Electronic excitation of C6H6 by positron impact, Rev Mex Fis 67: 188-192.
16. Lino JLS (2023) Excitation of the 21S, 21P and n = 3, 4, 5 (n1P) of Helium by positron impact. Int J At Nucl Phys 70: 28.
17. Varella MTN et al. (2001) New directions in Antimatter Chemistry and Physics. Kluwer, Amsterdam, 493.
18. Kadyrov AS, Bray I (2016) Recent progress in the description of positron scattering from atoms using the convergent close-coupling theory. Journal of Physics B 49: 222002.
19. Nahar SN (1989) Positronium formation during scattering of positrons by hydrogen atoms. Phys Rev A 40: 6231.
20. Lino JLS (2019) XXXI ICPEAC, Deauville, France, Abstract, 639.