Monte Carlo Simulation of 6MV Varian Clinac Photon Beam Using GEANT4-GATE

Abstract

Purpose: The primary aim of this study was the parameterization of our Geant4 Application for Tomographic Emission (GATE) linear accelerator (linac) model for the Varian Clinac 23 EX 6 MV photon beam via the comparison to the experimental PTW semiflex 31010 Percentage Depth Doses and cross-plane dose profiles for depths of d_max = 1.5, 5 and 10 cm for field sizes ranging from 30 × 30 to 3 × 3 cm² defined at isocenter.

Material methods: The GATE v7.0 geometric tools were used for designing the Varian Clinac 23 EX linac head according to manufacturer’s blueprints. Also, the GATE software tool Dose Actor divided the water phantom in dosels of 5 × 5 × 5 mm³ volume scoring the energy, dose and statistical uncertainty in each of them. The use of Bremsstrahlung Splitting technique with energy and direction filters was implemented for improving simulation efficiency but simultaneously conserving the physics accuracy of simulations. The vast number of simulations were run with the gate lab application of virtual imaging platform. The mean number of simulated electron particles in each simulation run was 7 billions and the mean simulation duration time 12 h.

Results: The mean energy of 6.2 MeV, the focal spot size of 1.4 mm and the flattening filter material density of 10.5 g cm^-3, were the final parameters values of our gate linac model that guarantee a good agreement to experimental ones, giving a simulation statistical uncertainty below 1%, local dose differences for cross plane dose profiles and PDDs, past the depth of maximum dose, better than 2% and identical beam quality index $\left(TP{R}_{10}^{20}\right)$.

Conclusions: The consistent set of the main characteristics of the initial electron beam and the flattening filter material density in combination with all gate parameters tested in a broad range of field sizes provides a well-validation of our gate linac model.

Keywords

GEANT4-GATE, Monte carlo, Simulation, Percentage depth dose, Dose profiles

Introduction

GATE (Geant4 Application for Tomographic Emission) [1] is a Monte Carlo (MC) simulation package developed by the open gate collaboration since 2001 and first publicly released in May 2004. Initially, it was developed and dedicated for modeling of Single Photon Emission Computed Tomography (SPECT) and Positron Emission Tomography (PET) imaging and acquisition applications. After the GATE V6 [2] release in February 2010, it was extended to the area of radiation therapy experiments and x-ray computed tomography.

In the present work, GATE V7.0 [3], released on April 2014, was used for the simulation of Varian Clinac 23 EX (Varian Medical Systems, Palo Alto, CA) linear accelerator (linac) for radiation fields ranging from 3 × 3 to 30 × 30 cm² defined at isocenter. There are some studies [4-7] that used different Monte Carlo general purpose codes [1,9] for the Varian Clinac 23 EX simulation but also for other similar Varian linac models and these were used as reference for the initialization of the parameters of the electron source beam of the present study, since linac specifications are hard to be found due to proprietary nature of information from manufacturers and vendors.

Due to this fact, a consistent set of the initial source electron beam characteristics as well as the flattening filter's density, forming the main linac parameters that influence the PDD curves and Dose profiles, was examined to be derived from experimental measurements through an iterative process of a vast number of MC simulations.

Materials and Methods

Varian Clinac 23 EX linac head geometry

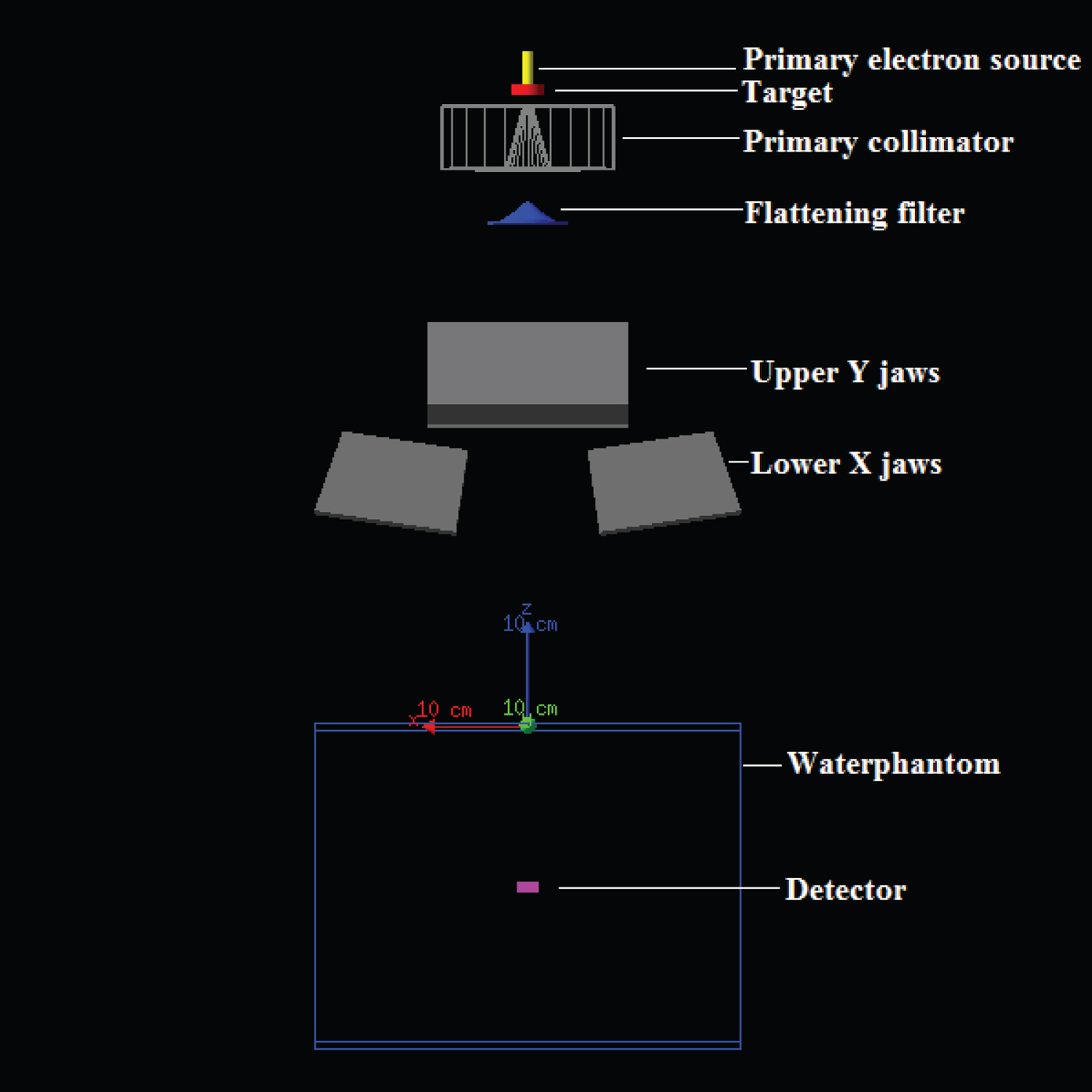
In the present work, a 6 MV photon beam of the Varian Clinac 23 EX linac is modeled, the geometry of which is depicted on (Figure 1), according to manufacturer's specifications. A Cartesian reference frame is defined such that the z axis coincides with the central beam axis and the origin of co-ordinates is located on isocenter of linac system on water phantom surface. The simulation starts at the moment that the primary source electrons hit the bremsstrahlung cylindrical tungsten target (manufacturer's nominal density: 17-19 gcm^-3). Consequently, bremsstrahlung photon beam is firstly collimated by the cylindrical tungsten primary collimator (manufacturer's nominal density: 18 g cm^-3) with a conical aperture and then is differentially attenuated by a conical flattening filter made of copper (manufacturer's nominal density: 8.92 g cm^-3). The monitor ion chamber and the mirror are excluded from the linac model since they slightly attenuate the photon beam (1-2%) [10] and no backscatter recording to these components is subject of the present study. Finally, two pairs of tungsten jaws (secondary collimators) (manufacturer's nominal density: 18 g cm^-3), upper - Y (rectangular shape) and lower - X (wedge shape) jaws limit the radiation field in y (transverse) and x (radial) directions, respectively. Afterwards, the finally attenuated flat photon fluence falls on the water phantom volume in order to give the expected measured dose distribution. Beyond the geometric shapes, materials and densities, the dimensions of the various linac components are not mentioned due to vendor's non-disclosable proprietary status.

The overall transport of each electron, incident on bremsstrahlung target, and all of its produced progeny (bremsstrahlung photon, knock-on electrons, positrons) tracked until the absorption in or exit of water phantom geometry is defined to as an event or a history [11,12]. As indicated later in the text (paragraph F.1), it is of great importance to consider all descendants associated with the ancestor electron as part of the same history, for calculating the quantity of interest, dose, in every dose scoring voxel (dosel) and its associated statistical uncertainty.

Primary source electron beam

The primary electron beam, produced by the electron gun tungsten filament and accelerated by the waveguide, gains a narrow energy, angular and spatial distribution, from now on called its main characteristics. Like most general MC codes [13,15] for clinical linacs, GATE/Geant4 starts modeling of the initial source electron fluence just above the target, forcing every user to make assumptions about its main characteristics, defining them through the General Particle Source (GPS) class [16] of the Geant4 software package.

The initial position of the primary source electrons was considered to be distributed on a curve with a Gaussian bell shape, as it is specified by manufacturers [5,6,17,18], oriented in x-y plane with square cross sectional profile, centered on central beam axis, with z position 0.1 mm above the bremsstrahlung target plane. The incident electron beam profile was assumed to be symmetric in x and y directions, because the measured data set consists of only cross-plane dose profiles. In GATE simulation tool kit, the parameter of the Gaussian positional distribution of primary electrons, responsible for affecting mainly the shape of dose profiles (flattened area, ‘horns' at profile sides and geometric penumbra) and being almost insensitive to depth dose curves [6,17-19], is corresponding to the Full Width of Half Maximum (FWHM) of focal spot size which is controlled by the standard deviation sigma_x, sigma _y in x and y directions respectively and given by the following equation:

$$FWHM=2\sqrt{2\ln \left(2sigma\_x\right)}\approx 2.355sigma\_x\left(1\right)$$

In the present study, according to vendors' nominal specifications and related researches and studies about Varian Clinac 23 EX linac model [7,17,18], the initial value of this parameter was set to FWHM = 1.2 mm and varied in the range of 0.9 to 1.5 mm during the iterative simulation process of matching the focal spot size. The energy distribution of the input primary source electrons was also assumed Gaussian and was spread about the mean energy with a FWHM equal to 3% of the latter [10]. The mean energy affects both the shape of dose profiles and depth dose curves and the position of maximum dose (D_max). According to bibliography [16], the initial value of mean energy was 6.2 MeV and was investigated in the range from 5.5 to 6.5 MeV. In terms of angular distribution, the source electron beam was supposed to be mono-directional [5,6,16,18], be parallel to central beam axis, travel along z axis and ‘fall' perpendicular on target plane.

The process of defining a consistence set of the incident electron beams characteristics (mean energy and focal spot size) requires a large number of simulations. Firstly, the mean energy, the only one of the main characteristics of the electron beam that affects strongly the PDD curves, matching was achieved by comparing the experimental and Monte Carlo calculated relative depth dose values, initially for the 30 × 30 cm² field size and later for the various field sizes used in the present work. Afterwards, since the mean energy matching is completed, the focal spot size is tried to be matched via the comparison of cross-plane relative dose profiles by varying the FWHM of this parameter for the larger field size (30 × 30 cm²) including in the experimental data set by simultaneously examining the whole flattening filter shape, volume and density. If the matching is not achieved to the desired precision level, then the mean energy and flattening filter's material density should be tuned in order to complete the matching. Finally, if the value of mean energy and flattening filter material density have been modified, new simulation runs must be performed with the final values of these parameters for confirming that the experimental and calculated relative depth dose curves continue to agree each other for the rest field sizes.

Physics settings

GATE incorporates the well-validated physics models and cross sections of Geant4 (Geometry and Tracking) MC general-purpose code [16] for simulating the electromagnetic (EM) interactions and random trajectories of individual particles in the matter. In Geant4, three EM packages of physics models are used for the photon and electron transport through media: Standard, Low-energy and Penelope [20]. For radiation therapy applications, and more specifically for the purpose of modeling the clinical accelerator treatment head of Varian Clinac 23 EX, standard package is recommended because, it is applicable for energies ranging from 1 KeV to the order of 100 TeV, employs simpler transport algorithms, uses parametrization methods of experimental data for cross sections computing [20] and more accurate physics models and has better Central Processing Unit (CPU) performance [21,22].

Geant4 standard package utilizes analog, [12] also called "event-by-event" or "interaction-by-interaction", simulation algorithms for handling the dominant photon EM physics processes in the energy range of interest for external beam radiotherapy: Photoelectric effect, compton (incoherent) scattering, Gamma conversion or pair production, excluding the coherent (Rayleigh) scattering and atomic relaxation processes [21]. In terms of charged particles, electrons and positrons, during their tracking into the matter they suffer a vast number of interactions (almost 10⁶/particle) divided in elastic (multiple coulomb scatterings) and inelastic interactions, including electron ionization, excitation and radiative (bremsstrahlung and positron annihilation) collisions. The latter energy loss processes produce an enormous number of secondary particles (soft and hard photons, knock-on electrons) which are simulated by a class II condensed history algorithm [12,23] improving simulation time. In terms of elastic collisions, Urban Multiple Scattering (MSC) model, based on Lewis theory is utilized [24].

Whenever production thresholds (AE for electrons/positrons and AP for photons) [23] are imposed in simulations, great care must be taken for the overall balance between photons and electrons, avoiding infrared divergence, [20,25] the implementation of class II condensed history algorithm and the trade-off between physics accuracy and CPU time performance. In the present study, AE and AP were both set to 1 mm for all treatment head components, whereas in the water phantom volume 3.0 mm and 1.0 mm corresponding to approximately 5 keV and 350 keV for photons and electrons/positrons respectively (Approximate Enhancing Improvement Techniques (AEIT)) [26]. Due to small number of photon interactions and fast photon transport and for the sake of physics accuracy, no transport energy cutoffs (PCUT) [23] for photons were set whereas for electrons and positrons, transport energy cutoffs, called ECUT [23], were imposed: 0.7 MeV for all simulation geometrical region of interest except for the target geometrical volume where the value was set to 1.5 MeV leading to decreasing the simulation time significantly [6].

In terms of simulation global options: The energy range of cross sections tables was set between 0.1 keV and 10 GeV, the number of bins of the dE/dx table was set to 210 (default value = 84) and the number of bins of the mean free path table was set to 210 (default value = 84) [25]. Finally, for electron step size limitations the following parameters were set: Step function, controlled by the variables drover range and final range, and linear loss limit set to default values and for geometrical step limit type the distance To boundary transport algorithm was selected [12,16,20,25,27].

EGI, VIP gate lab and parallelization

The accurate MC linac head simulation results with a desired statistical uncertainty level require a large number of statistically independent events, which are strongly influences the simulation computing time.

It must be specially mentioned that all simulations of the present study were run in VIP (Virtual Imaging Platform) [28] with the aid of gate lab application without the existence of which the present work would not be able to be carried out. And this is the fact because, for example a simulation of almost 7 billions of particles, the mean number of simulated particles used almost in all our simulations, lasts about 1 year in a pc of 3.2 MHz processor achieving simulation statistical uncertainty lower than 1%, whereas it lasts about 12 hours when this MC simulation is parallelized in 500 CPUs located at different geographical sites world-wide. VIP [28] 1) Is a web portal, 2) Is accessible at a specified URL (https://vip.creatis.insa-lyon.fr/), 3) Provides tools and services for medical simulations, 4) Comprises an appropriate operating framework of parallel splitting, merging and checkpoint programming strategies and 5) Is supported by the European Grid Infrastructure (EGI), a world-wide heterogeneous distributed computing infrastructure which is managed by special Random Number Generators (RNGs) producing unique random seeds, guaranteeing statistical independent merged final results from the various distributed farm of CPUs.

Of course, the simulation efficiency improvement is also achieved with the GATE's pseudo-random sequences that possess very long period RNGs of the order of 2¹⁴⁴. This makes the synchronism among different CPUs a rare coincidence.

Variance reduction techniques

Bremsstrahlung photons produced on the target are emitted isotropically. The proportion of the photon fluence, for a typical 6 MV photon beam of 10 × 10 cm² field size, that reaches the field of interest (patient or water phantom) is only about 2 to 3%. Thus, except for AEIT, such as transport cutoffs, true Variance Reduction Techniques (VRTs), i.e. that do not alter the physics when they improve the simulation efficiency [26], are necessitated in every simulation of linac head. GATE provides two commonly used VRTs, Splitting and Russian Roulette (J. von Neumann and S. Ulam) [29] specially used for linac head simulations.

In the present study, the Bremsstrahlung Splitting technique [3,20] was implemented improving simulation efficiency since the photons transport is quicker than the electrons' one in the Bremsstrahlung target. GATE provides the possibility to turn the splitting method to a selective one by adding various filters (energy, direction etc.) on primary electrons (primaries) and/or on secondary generated bremsstrahlung photons (secondaries). So, a bremsstrahlung splitting factor of 100 was implemented on primaries with energy greater than 1.0 MeV (energy filter), meaning that the final state (bremsstrahlung photons) of the bremsstrahlung physics process is generated 100 times and the statistical weight of each secondary photon is 1/100. The major advantage of this VRT is the fact that every initial electron with all its descendants belong to the same history. Also, a photon direction filter [2,3] was imposed on secondary generated Bremsstrahlung photons, meaning that only those emitted inside a cone centered on the beam axis (z axis) are being tracked. The angle between the beam axis and the edge of cone was set equal to 20° whereas the primary collimator's opening angle is 30°. Only these filtered secondary Bremsstrahlung photons have great possibility to reach the surface plane of water phantom and finally contribute to the calculated dose distribution. In this way, blocking some extra photons from tracking saves simulation time and increases simulation efficiency.

Monte carlo calculation uncertainties

Any MC calculation is subject to errors and uncertainties. Except for the MC inherent sources of error, such as the quality and accuracy of the available photon and electron cross section data, the systematic errors, i.e. programming errors, modeling inaccuracies, round-off and transaction errors and the voxel size effects [25] that cannot be evaluated, the statistical uncertainties due to stochastic nature of phantom dose calculation can be estimated.

Dose statistical uncertainty estimation: In GATE, software tool Dose Actor2 records three dimensional (3D) radiation therapy dose distributions in water phantom or patient volume. A user-defined matrix is attached to the rectangular volume of water tank dividing it into small dose scoring volume elements, called dosels, with volume size 5 × 5 × 5 mm³ equal to ionization chamber's active volume (0.125 cm³). Dose Actor uses these dosels - detectors in order to produce matrices which contain dose, squared dose and dose uncertainty assigned to each dosel with the aid of the history by history statistical analysis [11,30] by the following procedure: After simulating a number N of statistically independent particle histories, the scored quantity of interest, dose D_i in the dosel i, is estimated by the mean value ${\overline{D}}_i$, given by the following equation:

$${\overline{D}}_i=\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{D}_j}(2)$$

Where $D_j$ is the contribution to ${\overline{D}}_i$ due to the j history.

Of course, Dose Actor takes into account particle's statistical weight, 1 for primary ancestor particle and 1/n for secondaries, where n is the splitting factor. Also, a random point across the electron step line is selected where the dose is deposited.

Additionally, Dose Actor associates a statistical uncertainty ${\sigma }_{{\overline{D}}_i}$ to the mean value ${\overline{D}}_i$ of each dosel i. According to central limit theorem [31], the probability distribution to observe an expected value $〈D_i〉$ in a MC simulation will approach a Gaussian function in the limit of $\left(N\to \infty \right)$ or an infinite number of statistically independent particle histories, given by the following equation:

$${\sigma }_{{\overline{D}}_i}=\sqrt{\frac{1}{N}}\left(\frac{{\displaystyle {\sum }_{j=1}^N{D}_j^2}}{N}-{\overline{D}}_i^2\right)(3)$$

Where ${\sigma }_{{\overline{D}}_i}$ is the standard error of the mean dose ${\overline{D}}_i$ in dosel i.

The latter, ${\sigma }_{{\overline{D}}_i}$ is proportional to $\sqrt{{\overline{D}}_i}$. Fractional or relative statistical uncertainty $F_{D_i}$ is defined as the fraction $\frac{{\sigma }_{{\overline{D}}_i}}{{\overline{D}}_i}$ which is proportional to $1/\sqrt{{\overline{D}}_i}$ [12].

For characterizing the accuracy and overall statistical uncertainty of MC radiotherapy dose distributions (containing approximately some hundred thousands dosels or voxels) and simulations results, poor dose metrics such as statistical uncertainty of individual dosels such that of maximum dose voxel, $D_{\max }$, must be avoided due to their great statistical flactuation. Alternatively, the statistical uncertainties in dose averaged over some volume is recommended to be adopted such that of the fractional statistical uncertainty $F_{D>0.5D\max }$ suggested by Kawrakow, Rogers and Mohan [32] and given by the equation:

$$F_{D>0.5D\max }=\sqrt{\frac{1}{K_{D>0.5D\max }}{{\displaystyle {\sum }_{D>0.5D\max }\left(\frac{{\sigma }_{{\overline{D}}_i}}{{\overline{D}}_i}\right)}}^2}\left(4\right)$$

Where $F_{D>0.5D\max }$ represents the statistical uncertainty of the GATE simulation, $K_{D>0.5D\max }$ the number of dosels recording dose greater than 50% of maximum dose and $\frac{{\sigma }_{{\overline{D}}_i}}{{\overline{D}}_i}$ the relative statistical uncertainty of each dosel that participate in the summation.

After the GATE MC calculation of energy, dose and statistical uncertainty matrices by the Dose Actor software tool, the post processing of the final simulation results gathered from VIP Gate Lab is accomplished with Mat lab (R 2017b version) routines and Microsoft Excel (Microsoft Corp, Redmond, WA) data analysis software for obtaining the final form of PDDs and cross-plane dose profiles for comparison to corresponding experimental ones.

Experimental and GATE MC calculated beam quality index via $TP{R}_{10}^{20}$ value

Another parameter that characterizes a high energy photon beam is the well-known beam quality index which is expressed via Tissue Phantom Ratio $\left(TP{R}_{10}^{20}\right)$ [33] for a squared field of 10 x 10 cm² size, and also is defined by the following equation:

$$TP{R}_{10}^{20}=1.2661\times PD{D}_{10}^{20}-0.0595\left(4\right)$$

Where $PD{D}_{10}^{20}$ is the ratio of doses at depth of 20 cm and 10 cm easily determined from the PDD of the 10 × 10 cm² field size defined at the isocenter. This value was found experimentally as well as in GATE MC by the help of equation (4).

Measured dosimetric data used for MC model validation

The dosimetric measurements were carried out at the radiation therapy department of metropolitan hospital, Piraeus, Greece as part of the annual quality assurance (QA) program, including procedures according to task groups 106 [33] and 51 [34] of the therapy physics committee of the american association of physicists in medicine.

The 6 MV photon beam, produced by the Varian Clinac 23 EX Clinac, irradiated the scanning water tank with dimensions 48 × 48 × 48 cm³ and walls made of PolyMethyl MethAcrylate (PMMA) material (density 1.18 g cm^-3). The Clinac Source to water Surface Distance (SSD) was kept constant to 100 cm for all measurements. An ionization chamber Semiflex 31010 (PTW-Freiburg, Germany) with active volume of 0.125 cm³ was used and the scanning resolution was 1 mm.

The measured data set consists of Percentage Depth Dose (PDDs) curves and cross-plane (transverse x axis perpendicular to Gantry - Target (GT) direction) dose profiles for various open field sizes: 3 × 3, 4 × 4, 10 × 10, 20 × 20 and 30 × 30 cm², defined at isocenter and for depths: D_max = 1.5, 5 and 10 cm, comprising a wide range of field sizes necessitated for well-validation of our GATE linac model. The normalization of dose was done at maximum dose (D_max = 1.5 cm) for PDDs and at mean dose of 80% of flattened dose profile area for cross field dose distributions. The raw measured data were collected and processed by the OmniPro Accept by Scanditronix Wellhöfer AB aquisition and analysis software. In the current study, it is specially mentioned that no de-noised methods or other filters are implemented to GATE MC calculated data. The calculated and measured data were compared in terms of relative dose values, via the local dose difference, and not the absolute ones in order to get a consistent set of the main characteristics (mean energy and focal spot size) of the initial electron beam incident on the target plane as well as flattening filter density. The local dose difference is defined as the percentage difference between the calculated and reference value of the dose at a single point.

Results

MC Model validation vs. measured PDDs

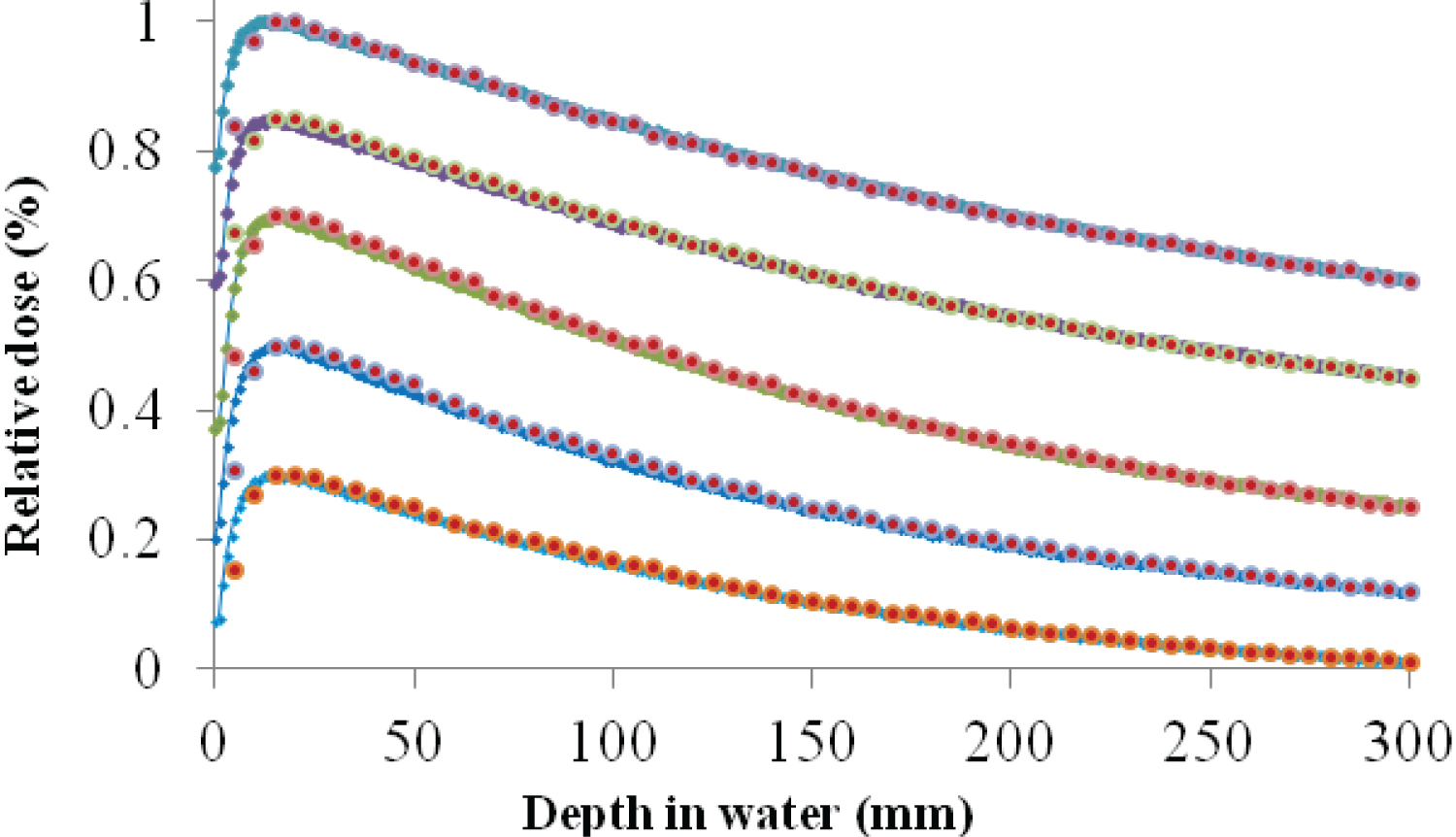
Figure 2 shows the PDDs for all field sizes examined in the present work. For visualization purpose the results were rescaled, the larger's field size (30 × 30 cm²) PDD was normalized to the value of 1 and the smallest's one (3 × 3 cm²) to 0.3. The statistical uncertainty $\left(F_{D>0.5D\max }\right)$ for the simulated field size a) 30 × 30 cm², b) 20 × 20 cm², c) 10 × 10 cm², d) 4 × 4 cm² and e) 3 × 3 cm² was a) 0.83%, b) 0.63%, c) 0.97%, d) 0.99% and e) 1.02% respectively. The GATE PDD curves are all in good agreement with the experimental ones past the depth of maximum dose (d_max), with the absolute percentage local dose difference not exceeding 2%. In contrary, in terms of the build-up region the electron contamination phenomenon caused large percentage local dose differences. For reaching these results, the values of the main characteristics of the initial electron beam hitting the tungsten target were: The mean energy 6.2 MeV and the FWHM electron spot size 1.4 mm and furthermore flattening filter material (Cu) density was set to 10.5 gcm^-3 whereas the vendor's specification of the linac was 8.92 gcm^-3. After a vast number of simulations, it was observed that the mean energy of the initial electron's beam played the determining role in defining the position of maximum dose, d_max. Also, it was concluded that increasing the FWHM of the radial intensity distribution, i.e. increasing the intensity of the photon beam on the central axis, a dose bump was added in shallowest depths about 2 cm after the d_max for all field sizes and almost insensitive to the rest PDD curve. Finally, there must not be ignored the relatively big influence of flattening filter density on reaching this good agreement. And this was so because by increasing the density of copper, the resulted beam hardening was definitely played a significant role for altering the shape of depth dose curve for larger depths by minimizing the depth local dose differences between GATE and reference data for all examined field sizes.

Figure 2 Percentage Depth Dose (PDD) curves for all field sizes studied in the present work. GATE/Gean4 simulated results are depicted by the red dots and experimental ones by the lines with small blue diamonds. For visualization purpose, PDDs are rescaled with the highest curve (normalized to 1) corresponding to greater field size (30 × 30 cm²) and the lowest one (normalized to 0.3) corresponding to 3 × 3 cm².

MC Model validation vs. measured OARs

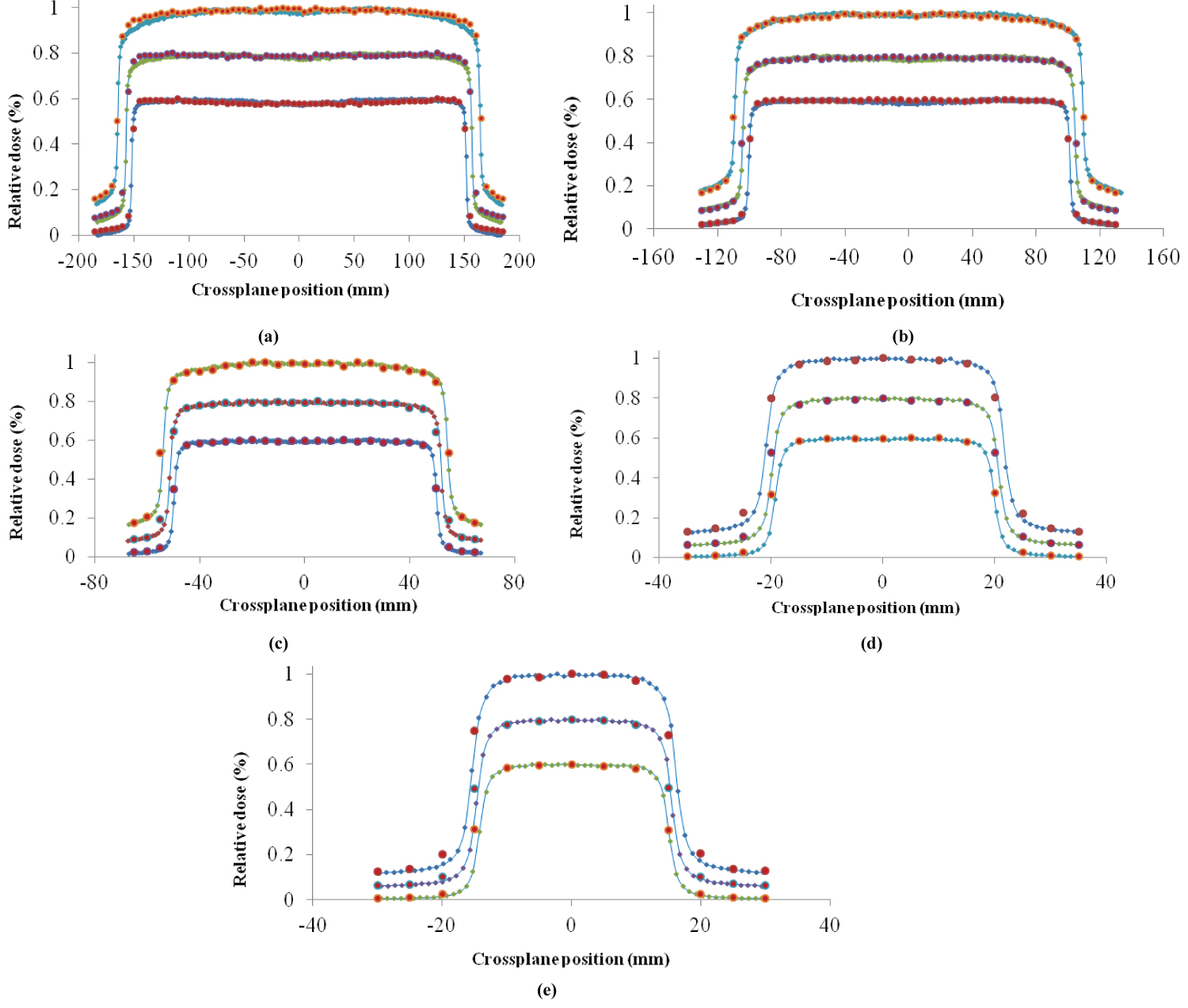
The GATE MC calculated cross-plane dose profiles versus experimental ones are represented in Figure 3 for field sizes a) 30 × 30 cm², b) 20 × 20 cm², c) 10 × 10 cm², d) 4 × 4 cm² and e) 3 × 3 cm² examined and for the depths of d_max: 1.5 , 5 and 10 cm, with simulation statistical uncertainty $\left(F_{D>0.5D\max }\right)$ a) 0.83%, b) 0.63%, c) 0.97%, d) 0.99% and e) 1.02% respectively. In terms of dose profiles, both of the main characteristics of the primary electron beam and flattening filter material density influence their shape. Specifically, the FWHM of the electron spot size and the mean energy of the primary electron beam influence both the ‘horns' and the penumbra of cross-plane profiles. More specifically, by increasing the mean energy the ‘horns' decrease while the penumbra increases. Increasing the FWHM of the radial intensity distribution of the primary electron beam causes the same effect. Finally, the flattening filter material density plays a significant role on the flattened dose profile area, by decreasing the ‘horns' and central beam axis dose values when the copper density decreases. As depicted on the following diagrams, there is great agreement between the calculated and measured results, observing a little divergence in the horns of 30 × 30 cm² dose profiles for the depth of 10 cm, a fact which reveals that the sensitivity of electron source main characteristics and the flattening filter's density on dose profile vanishes by increased field size and depth where the phantom scatter dominates.

Figure 3 GATE Monte Carlo vs Experimental Cross-plane dose profiles for all field sizes a) 30 × 30 cm², b) 20 × 20 cm², c) 10 × 10 cm², d) 4 × 4 cm² and e) 3 × 3 cm² and for depths: D_max: 1.5 cm, 5 cm and 10 cm. For visualization purpose, the results were rescaled with profiles of greater depth (10 cm) corresponding to 1, next depth (5 cm) to 0.8 and the shallower depth d_max to 0.6. Simulation Statistical uncertainty of all above field sizes is: a) 0.83%, b) 0.63%, c) 0.97%, d) 0.99% and e) 1.02%.

MC Model validation vs. Beam quality index $\left(TP{R}_{10}^{20}\right)$ value

The MC GATE calculated and experimental beam quality index was found almost identical as shown in the Table 1 below, referred to simulated field size 10 ˟10 cm² with simulation statistical uncertainty $\left(F_{D>0.5D\max }\right)$ of 0.97%.

Discussion and Conclusion

The goal of this study was the design of the model for a 6 MV Varian Clinac 23 EX photon beam using Geant4 - GATE v.7.0 by comparing MC calculated PDD curves and transverse dose profiles with water experimental measurements for field sizes ranging from 3 × 3 to 30 × 30 cm². The parameters examined for our GATE linac model were the initial electron beam characteristics (mean energy and focal spot size) and flattening filter material density. The simulations were performed from bremsstrahlung tungsten target to water phantom. The latter's volume was subdivided into 5 × 5 × 5 mm³ dosels by the GATE software tool Dose Actor for scoring dose, squared dose and statistical uncertainty in each dosel. The Bremsstrahlung Splitting (BS) tool in combination with filters (energy, direction) was also implemented in order to improve simulation efficiency.

The mean number of simulated primary particles for the vast number of all simulations was 7 billions, all performed in VIP by the gate lab application, the mean simulation time was 12 h and the simulation statistical uncertainty $\left(F_{D>0.5D\max }\right)$ was better than 1%, and the local dose difference for both PDDs (past the depth of maximum dose) and transverse dose profiles was lower than 2%. There is only disagreement for all PDDs from water surface to the depth of maximum dose due to electron contamination that could not best simulated and of course due to spatial resolution since voxel - dosel side size is 5 mm and not smaller. Finally, there is another mismatch for the increased ''horns"' for the dose profile of 30 × 30 cm² for the depth of 10 cm. This is due to the fact that for these increased field size and depth phantom scatter dominates.

The good agreement between GATE results and experimental measurements in combination with the wide range of examined simulation field sizes guarantee the well-validation of our GATE linac model of the Varian Clinac 23 EX.

Our future aim is to implement our GATE linac model of the Varian Clinal 23 EX in small field dosimetry.

Acknowledgments

The authors extend their appreciation to the International Scientific Partnership Program ISPP at King Saud University for funding this research work through ISPP 150.

Conflicts of Interest

No.

References

1. Jan S, Santin G, Strul D, et al. (2004) Gate: A simulation toolkit for pet and Spect. Phys Med Biol 49: 4543-4561.
2. Jan S, Benoit D, Becheva E, et al. (2010) GATE V6: A major enhancement of the GATE simulation platform enabling modelling of CT and radiotherapy. Phys Med Biol 56: 881-901.
3. Open GATE collaboration organization. Documentation and Recommendations for Users.
4. Ding G X (2002) Energy spectra, angular spread, fluence profiles and dose distributions of 6 and 18 MV photon beams: Results of monte carlo simulations for a Varian 2100 EX accelerator. Phys Med Biol 47: 1025-1046.
5. Sheikh-Bagheri D, Rogers DWO (2002) Sensitivity of megavoltage photon beam monte carlo simulations to electron beam and other parameters. Med Phys 29: 379-390.
6. Keall P J, Siebers J V, Libby B, et al. (2003) Determining the incident electron fluence for monte carlo-based photon treatment planning using a standard measured data set. Med Phys 30: 574-582.
7. Jutemark B (2005) Monte carlo based investigation of the influence of accelerator- head geometry on megavolt photon beam quality in radiotherapy. PhD Thesis, Lund University, Lund, Sweden.
8. Nelson W R, Hirayama H, Rogers DWO (1985) The EGS4 Code System, Report SLAC-265, Stanford Linear Accelerator Center, Stanford, California.
9. Rogers DWO, Faddegon B A, Ding G X, et al. (1995) BEAM: A monte carlo code to simulate radiotherapy treatment units. Med Phys 22: 503-524.
10. Verhaegen F, Seuntjens J (2003) Monte carlo modeling of external radiotherapy photon beams. Phys Med Biol 48: 107-164.
11. Walters BRB, Kawrakow I, Rogers DWO (2002) History by history statistical estimators in the BEAM code system. Med Phys 29: 2745-2752.
12. Chetty I J, Curran B, Cygler J E, et al. (2007) Report of the AAPM task group no. 105: Issues associated with clinical implementation of monte carlo-based photon and electron external beam treatment planning. Med Phys 34: 4818-4853.
13. Kawrakow I, Rogers DWO (2000) The EGSnrc code system: Monte Carlo simulation of electron and photon transport. Technical Report PIRS-701, National Research Council of Canada, Ottawa, Ontario, 2000.
14. Brown FB (2003) MCNP - A general Monte Carlo-particle transport code, version 5. Report LA-UR-03 1987, Los Alamos National Laboratory, Los Alamos, NM.
15. Baro J, Sempau J, Fernandez-Varea JM, et al. (1995) PENELOPE: An algorithm for monte carlo simulation of the penetration and energy-loss of electrons and positrons in matter. Nucl Instr Meth Phys. Res 100: 31-46.
16. Agostinelli S, Allison J, Amako K, et al. (2003) Geant4 - a simulation toolkit. Nucl Instr Meth Phys Res 506: 250-303.
17. Karzmark C J, Nunan C S, Tanabe E (1993) Medical electron accelerators. McGraw-Hill, New York.
18. Jaffray D A, Battista J J, Fenster A, et al. (1993) X-ray sources of medical linear accelerators: Focal and extra-focal radiation. Med Phys 20: 1417-1427.
19. Sheikh-Bagheri D, Rogers D W O, Ross C K, et al. (2000) Comparison of measured and Monte Carlo calculated dose distributions from the NRC linac. Med Phys 27: 2256-2266.
20. GEANT4 Collaboration. User documentation. Physics Reference Manual.
21. Poon E, Verhaegen F (2005) Accuracy of the photon and electron physics in Geant4 for radiotherapy applications. Med Phys 32: 1696-1711.
22. Grevillot L, Frisson T, Maneval D, et al. (2011) Simulation of a 6 MV Elekta Precise Linac photon beam using GATE/GEANT4. Phys Med Biol 56: 903-918.
23. Berger J, Fernbach S, Alder B, et al.(1963) Methods in computational physics. Academic, New York.
24. Rogers D W O, Bielajew A F (1990) The dosimetry of ionizing radiation. Academic, New York, 427-539.
25. Lewis H W (1950) Multiple scattering in an infinite medium. Phys Rev 78: 526.
26. Sheikh-Bagher D, Kawrakow I, Walters B. Monte carlo simulations: Efficiency improvement techniques and statistical considerations.
27. Apostolakis J, Asai M, Bogdanov A G, et al. (2009) Geometry and physics of the Geant4 toolkit for high and medium energy applications. Radiat Phys Chem 78: 859-73.
28. Camarasu-Pop S, Glatard T, Ferreira da Silva R, et al. (2013) Monte-carlo simulation on heterogeneous distributed systems: A computing framework with parallel merging and check pointing strategies. Future Generation Computer Systems 29: 728-738.
29. Kahn H (1956) Use of different monte carlo sampling techniques. In: H A Meyer, Symposium on monte carlo methods. John Wiley and Sons, New York, 146-190.
30. Sempau J, Sanchez-Reyes A, Salvat F, et al. (2001) Monte carlo simulation of electron beams from an accelerator head using PENELOPE. Phys Med Biol 46: 1163-1168.
31. Lux I, Koblinger L (1991) Monte carlo particle transport methods: Neutron and photon calculations. CRC Press, New York.
32. Rogers D W O, Mohan R (2000) Questions for Comparison of Clinical Monte Carlo Codes. In: XIIIth International Conference on the Use of Computers in Radiation Therapy (XIIIth ICCR). W Schlegel and T Bortfeld (eds.). Heidelberg: Springer-Verlag pp.120-122.
33. Das J I, Cheng C W, Watts R J, et al. (2008) Accelerator beam data commissioning equipment and procedures: Report of the TG-106 of the therapy physics committee of the AAPM. Med Phys 35: 4186-4215.
34. McEwen M, DeWerd L, Ibbott G, et al. (2014) Addendum to the AAPM’s TG-51 protocol for clinical reference dosimetry of high-energy photon beams. Med Phys 41: 041501.