The Stability of a Gravitational Globular Cluster

Abstract

We use non-equilibrium statistical mechanics to model a globular cluster and find that for our initial condition, the globular cluster may be unstable.

Introduction

Recent observations reporting 60 globular clusters or faint galaxies orbiting the Milky Way [1] open up the question of whether globular clusters exist only within galaxies. In this work, we examine the time evolution of an isolated globular cluster and raise the issue of its stability.

To begin, we assume that stars are assumed to be self-gravitating point particles.

Our analytic approach will use the first two terms of a six-term time evolution equation for the one-particle distribution function $f\left(r,p,t\right)$ [2] using the gravitational pair-potential V

$$f\left(r,p,t\right)\text{ = }f\left(r-\frac{pt}{m},p,0\right)+{\displaystyle {\int }_0^{t}d{s}_1}{e}^{-s_1{L}_o}f\left(r,0\right){\displaystyle \int dr}\text{'}\left(\frac{\partial V\left(r-r\text{'}\right)}{\partial r}\right)f\left(r\text{'},0\right)\frac{\phi \left(p,0\right)}{\partial p}\left(1\right)$$

Where $L_o\text{ = }\frac{p}{m}\frac{\partial }{\partial r}$. $r,p$ are phase space variables, $\phi \left(p,0\right)$ is the initial momentum distribution. The density of the cluster as a function of $r,t$ may be calculated by integration over momentum.

We will display the time evolution of the density of a globular cluster for a specific initial data, with the hope of modelling its time evolution for various other initial conditions.

Let the initial data $f\left(r,0\right)\text{ = }\sqrt{\frac{a}{\pi }}{e}^{-a{r}^2},$ $f\left(r\text{'},0\right)\text{ = }\sqrt{\frac{a}{\pi }}{e}^{-ar{\text{'}}^2},$ $\phi \left(p,0\right)\text{ = }\sqrt{\frac{b}{\pi }}{e}^{-b{p}^2}$

$$f\left(r-pt/m,p,0\right)\text{ = }f\left(r-pt/m\right)\phi \left(p,0\right)\left(2\right)$$

The free particle contribution to the total density is the integral of (1) over momentum. For the free-particle contribution to the density, we get

$${\rho }_o\text{ = }{\displaystyle \int dp}f\left(r-pt/m,p,0\right)\text{ = }{\displaystyle {\int }_{-\infty }^{\infty }f\left(r-pt/m\right)\phi \left(p,0\right)\text{ = }\sqrt{\frac{ab}{\pi }}}\frac{e^{-\frac{\text{a}{m}^2{r}^2\text{b}}{a{t}^2+b\ast m^2}}}{\sqrt{a{t}^2+b{m}^2}}\left(3\right)$$

The contribution of the gravitational interaction to the density is obtained from the second term of Equation (1)

$${\rho }_1\text{ = }{\displaystyle {\int }_0^{t}d{s}_1}{e}^{-s_1{L}_o}f\left(r,0\right){\displaystyle \int dr\text{'}\left(\frac{\partial V\left(r-r\text{'}\right)}{\partial r}\right)f\left(r\text{'},0\right)\frac{\phi \left(p,0\right)}{\partial p}}\left(4\right)$$

which we evaluate step by step from right to left.

As a consequence of Newton's shell theorem for a spherically symmetric system, we may write

$$\begin{array}{l}{\displaystyle \int dr\text{'}\left(\frac{\partial V\left(r-r\text{'}\right)}{\partial r}\right)f\left(r\text{'},0\right)\text{ = 4}\ast Pi}\ast G\ast no{\displaystyle {\int }_0^{r}dr\text{'}}f\left(r\text{'},0\right)r{\text{'}}^2/r{\text{'}}^2\\ \text{ = 4}\ast Pi\ast G\ast no{\displaystyle {\int }_0^{r}dr\text{'}}f\left(r\text{'},0\right)\left(5\right)\end{array}$$

For a Gaussian initial density distribution, the integral of $r\text{'}$ may be evaluated, using the initial one-particle distribution $$f\left(r\text{'},0\right)$$. The shift operator acts on everything to its right by substituting $r-ps1/m$ for r.

The integral over s1 becomes

$$\frac{2\pi bGm{n}_o}{a}\frac{\sqrt{ab}}{\pi }\left(e^{-2a{r}^2-b{p}^2}-e^{-\frac{2m{a}^2{r}^2-4amprt+2a{p}^2{t}^2+b{p}^2{t}^2}{m^2}}\right)$$

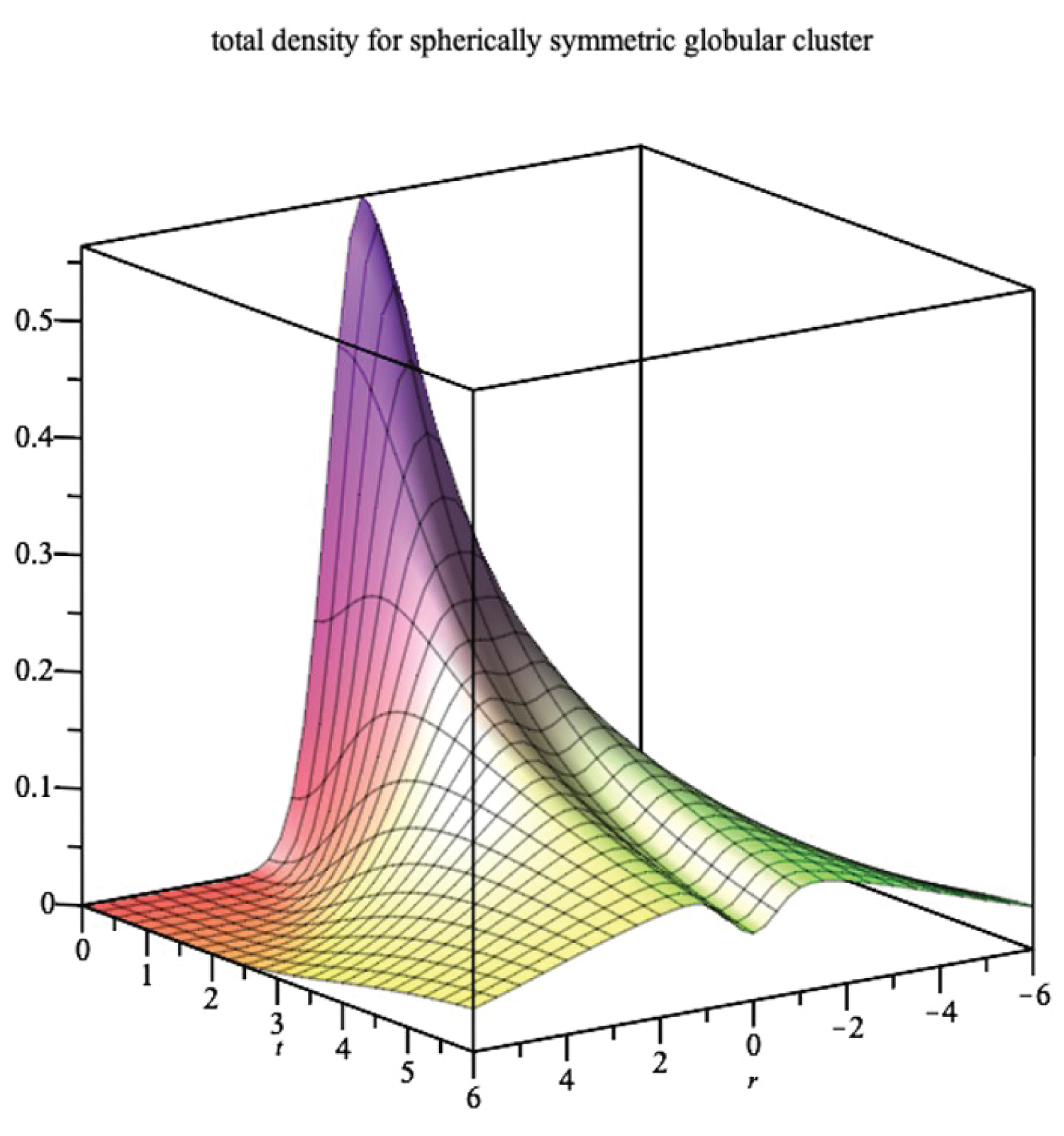
The contribution to density of the gravitational interaction is the integral over momentum of the expression above, integrated numerically. The contribution of the gravitational interaction to the density is shown in Figure 1. It shows the birth of two sub-clusters for the initial data we picked.

With our chosen initial data, the globular cluster will be unstable, breaking up into two clusters. It would be interesting to investigate other initial data to determine the long-term behavior of the cluster. With this paper we begin a program of studying the evaporation of stars from clusters.

References

1. Simon JD, Geha M (2021) Illuminating the darkest galaxies. Physics Today 74: 30.
2. Muriel A (2016) Time evolution equations for hydrodynamic variables with arbitrary initial data. Results in Physics 6: 252-255.