Idiopathic Macular Hole Complexity: A Simplified Mathematical Model Judged on Optical Coherence Tomography Morphology

Abstract

Objectives

To determine a mathematical relationship and complexity factor for macular hole morphology on optical coherence tomography.

Methods

Ninety eyes from 90 patients who underwent successful primary macular hole surgery between 1 January 2014 - 31 December 2018 at Christchurch Hospital, New Zealand were retrospectively analyzed, with the fellow eye as the control. In addition, 10 eyes not closing at primary surgery have been analyzed. Mathematical analysis was performed using GetData Graph Digitizer version 2.26 and the automated symbolic regression software Eureqa version 1.24. The study was conducted following the principles of the declaration of Helsinki.

Results

Mean age was 74 (± 9) years. Stage of macular hole was small: 24 (27%), medium: 34 (38%), and large: 32 (35%). The mathematical regression function was of complexity 36 (± 6) for small, 108 (± 10) for medium, and 169 (± 14) for large (p = 0.03). The level of complexity reduced to 10 (± 5), 16 (± 9), and 11 (± 1), respectively postoperatively (p < 0.005). Complexity values were strongly correlated with macular hole stage (r = 0.8, p = 0.05) and with preoperative visual acuity (r = 0.8, p < 0.005). For the unaffected fellow eye, the complexity was 15 (± 3) for small, 31 (± 11) for medium, and 13 (± 3) for large.

Conclusions

Complexity scores increased with increasing macular hole stage. Our findings suggest the complexity measurements are an indirect assessment of the stresses, exposure and subsequent dysfunction the macula is undergoing.

Introduction

Optical coherence tomography (OCT) has transformed our understanding and management of macular and retinal pathologies. The pathogenesis of idiopathic macular hole (MH) is said to be linked to hyaloid adhesions and vitreomacular traction (VMT), which result in anteroposterior and tangential traction.

With the advent of OCT and its widespread use, the description, features and stages of MHs have undergone a transition. Analyses of MHs on OCT have resulted in interesting observations. It was found in the fellow eyes of MH eyes that posterior hyaloid detachment begins around the macula, but the hyaloid remains adherent to the foveolar center, producing anteroposterior forces. An intraretinal split results and evolves into a cystic space, and then further disruption of the outer retinal layer and the opening of the foveal floor leads to a full thickness MH [1]. The vitreous is responsible for some of the offending forces causing MH development. What is not clear is why MH progression still occurs after complete posterior vitreous detachment (PVD) when there is complete vitreous separation evident on OCT and a Weiss ring seen on slit lamp biomicroscopy. This suggests that other residual tractional forces are responsible for keeping a MH open and its subsequent enlargement. Since the widespread use of OCT some anecdotal descriptions of MH morphology have become commonplace. A means of quantifying MH morphology is important, and mathematical analysis of morphological subtypes will improve our understanding of MH formation, progression and treatment.

Subjects and Methods

This study was approved by the Northern A Health and Disability Ethics Committee of New Zealand. The aim was to mathematically analyze the complexity of a MH before and following surgery with vitrectomy, internal limiting membrane (ILM) peel and gas tamponade. The hypothesis being that a mathematical relationship exists and could be represented by a complex regression formula, and furthermore, the complexity of the formula can be represented as a more tangible numerical value. We hypothesize that MH stage is correlated to this complexity value.

Stages of PVD were determined using the following; stage 0: no PVD, stage 1: Perifoveal vitreofoveal adhesion (VFA); stage 2: Perifoveal PVD and no VFA; stage 3: Complete PVD except for vitreopapillary adhesion, stage 4: Complete PVD [2]. Macular hole contour was analyzed from images acquired on the Canon OCT-HS100 scanner and classification was based on the International Vitreomacular Traction Study Group guidance as small (< 250 microns), medium (250-400 microns), and large (> 400 microns) [3].

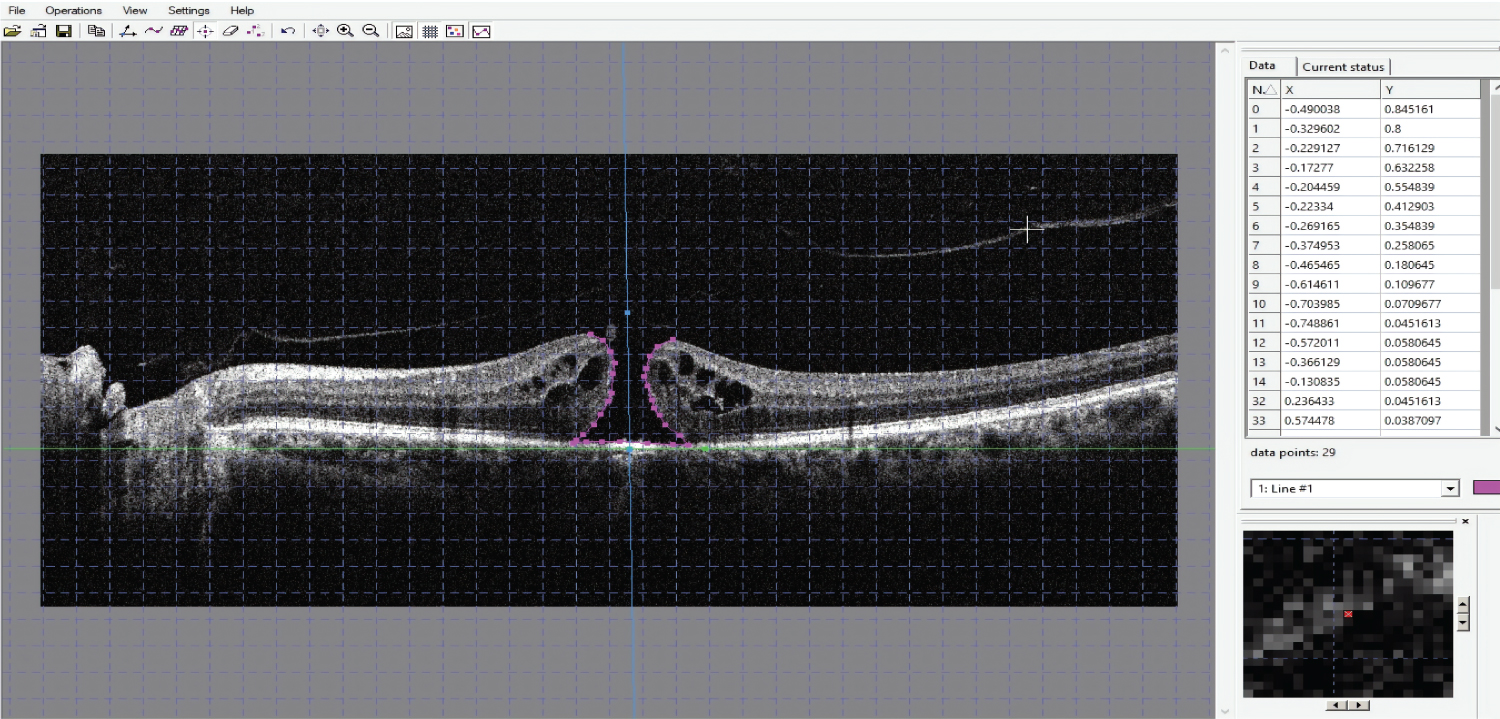
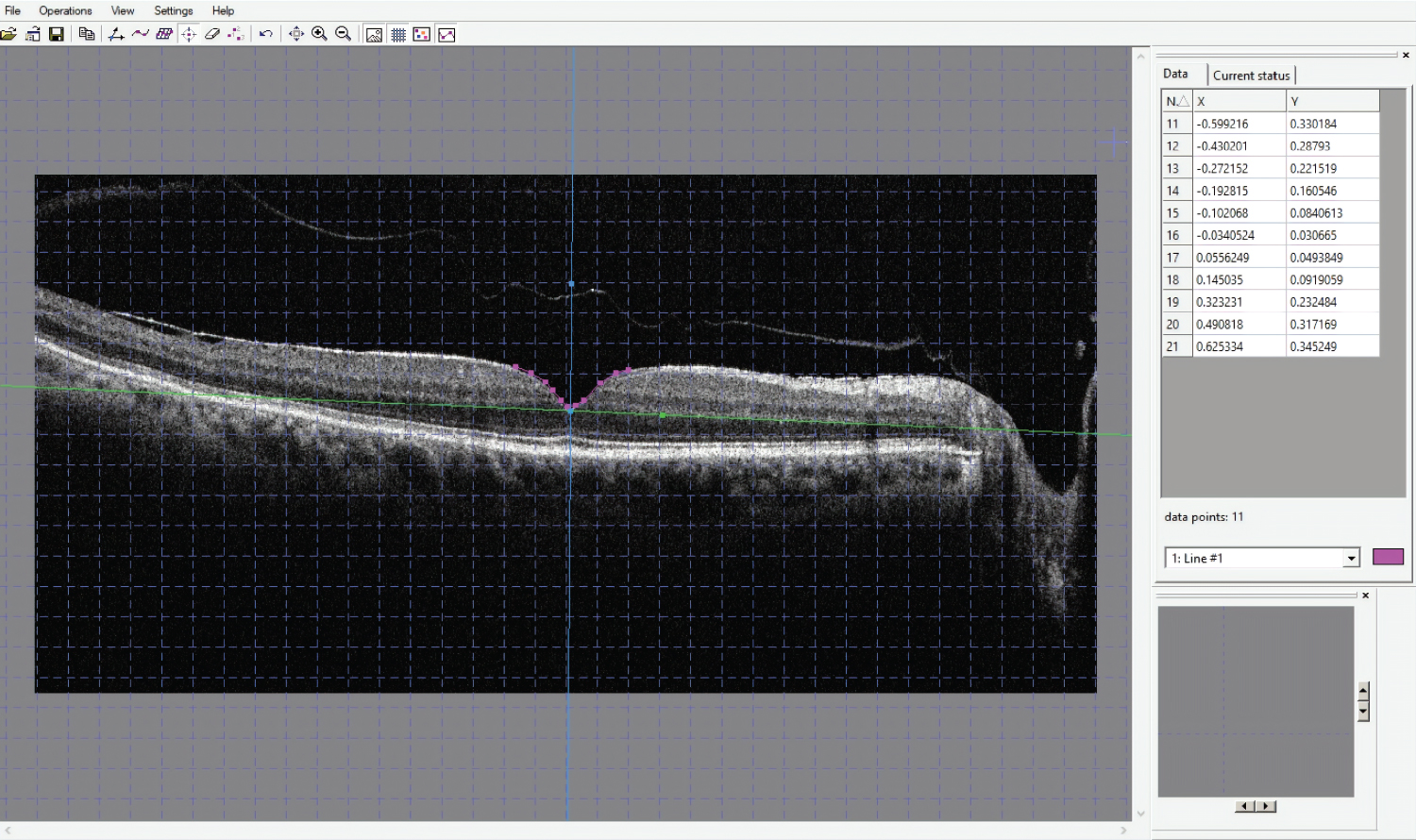
The MH, fellow eye and postoperative MH contour were determined using the computer software GetDataGraph Digitizer version 2.26, S Fedorov. This software allows digitalizing of graphs and plots from the supported graphics formats, which is Joint Photographic Experts Group (JPEG) in our study. The process involved importing JPEG images of the OCT images, plotting the x and y axes, and manually plotting the contour of the MH. Figure 1 and Figure 2 show the plots and outputs used. These data were used for further analysis.

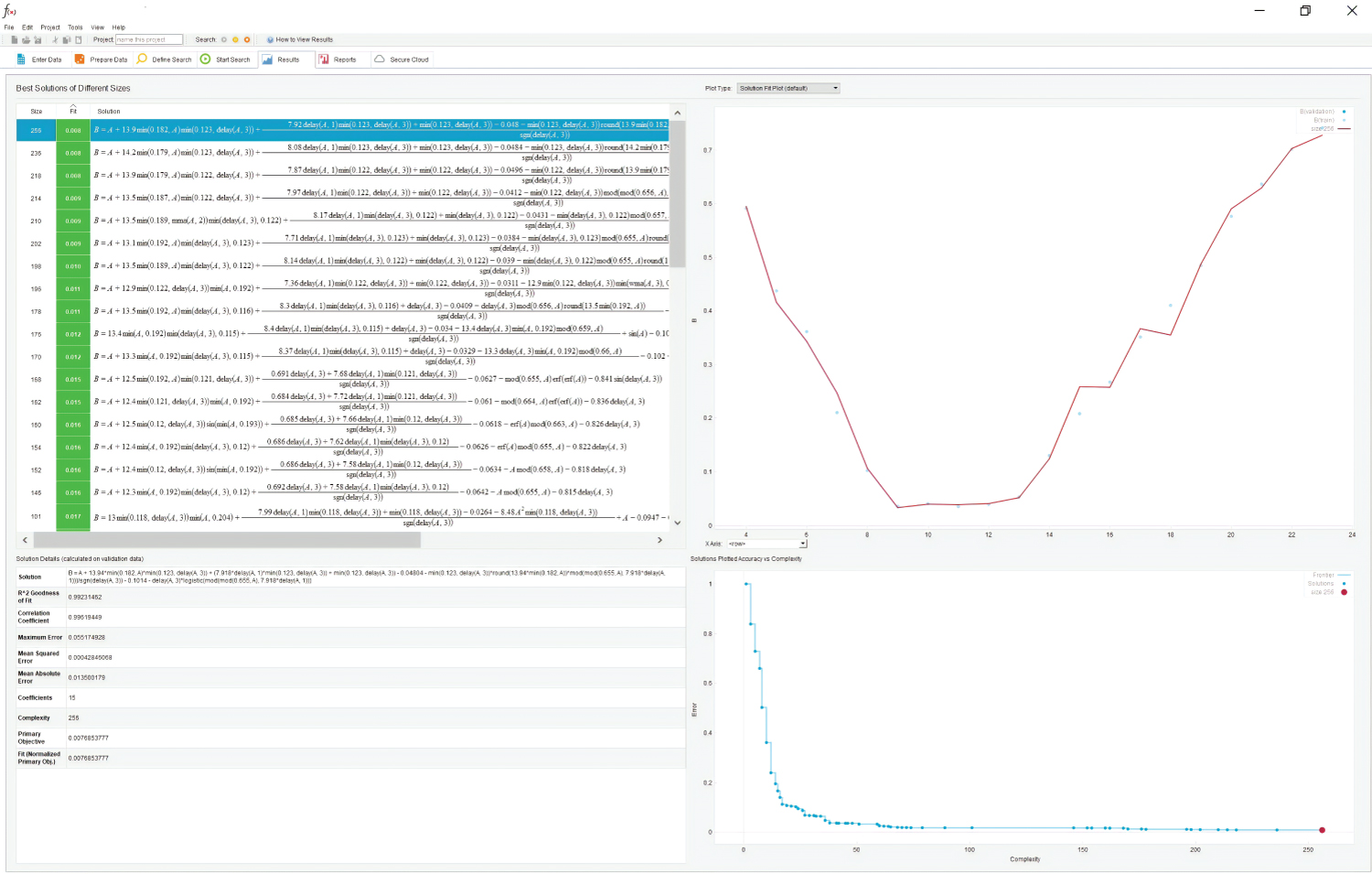
Using data plots acquired from the GetData output, a mathematical analogue of MH and foveal contour was obtained using the automated symbolic regression software Eureqa version 1.24 (Nutonian, Boston, MA, USA) [4,5]. This dynamic modelling engine analyses billions of potential solutions per second [5]. A fit to 0.070 was used for our study. The R-squared goodness of fit was used as the main error metric. All potential mathematical formula building blocks were used in the formula search. Where a solution was not uncovered within 10 minutes, the program would be left to compute a solution over 12 hours. Figure 3 shows the typical output.

Along with the OCT data, basic demographic data, duration of MH, preoperative best corrected visual acuity (BCVA), postoperative BCVA, surgery details, outcome, axial length, refraction, lens status, intraoperative and postoperative complications were also recorded.

Exclusion criteria included gross structural macular abnormalities, previous vitreoretinal surgery, previous complicated cataract surgery and any other cause of a MH other than idiopathic.

SPSS Statistics version 20.0 (IBM Corporation, Armonk, NY, USA) was used for data analysis. Descriptive analysis was carried out. For group comparison: two paired t-test and ANOVA with a p < 0.05 was considered significant. Spearman rank was used for correlation analysis.

Results

Ninety eyes undergoing MH surgery are included in this analysis, with the fellow eye as the control. Ten fellow eyes were excluded from the analysis due to a previous history of MH surgery (6 eyes), macular pathology (3 eyes), and trauma (1 eye). In addition, 10 eyes requiring redo MH surgery have been included in the analysis. Mean age was 74 (± 9) years, and 64% (n = 58) were female. All patients in our study were Caucasian. Grouping showed 24 (27%) small (S), 34 (38%) medium (M), and 32 (35%) large (L) holes.

Mean preoperative Logarithm of the Minimum Angle of Resolution (LogMAR) BCVA was 0.66 (± 0.2) for S, 0.76 (± 0.1) for M, and 0.88 (± 0.2) for L holes. Postoperatively, it was 0.16 (± 0.15) for S, 0.36 (± 0.2) for M, and 0.50 (± 0.4) for L. These changes were statistically significant (p = 0.02). Preoperative MH duration in months was 4 (± 2) for S, 9 (± 3) for M, and 10 (± 9) for L.

The mathematical regression function was of complexity 36 (± 6) for S, 108 (± 10) for M, and 169 (± 14) for L (p = 0.03). Postoperatively, the level of complexity reduced to 10 (± 5), 16 (± 9), and 11 (± 1) for S, M, and L holes, respectively (p < 0.005).

The stages of PVD in the MH eyes were stage 1: 29% (n = 26), stage 3: 38% (n = 34), and stage 4: 33% (n = 30). No statistical relationship was found between the stage of PVD and the MH complexity (p = 0.23). The stage of MH and complexity were strongly correlated (r = 0.8, p = 0.05).

Preoperative BCVA was strongly correlated to the complexity of the MH (r = 0.8, p < 0.005), but this did not reach statistical significance for MH stage (r = 0.55, p = 0.18). When the MH duration was compared to the MH complexity, this was not statistically significant (r = 0.52, p = 0.08).

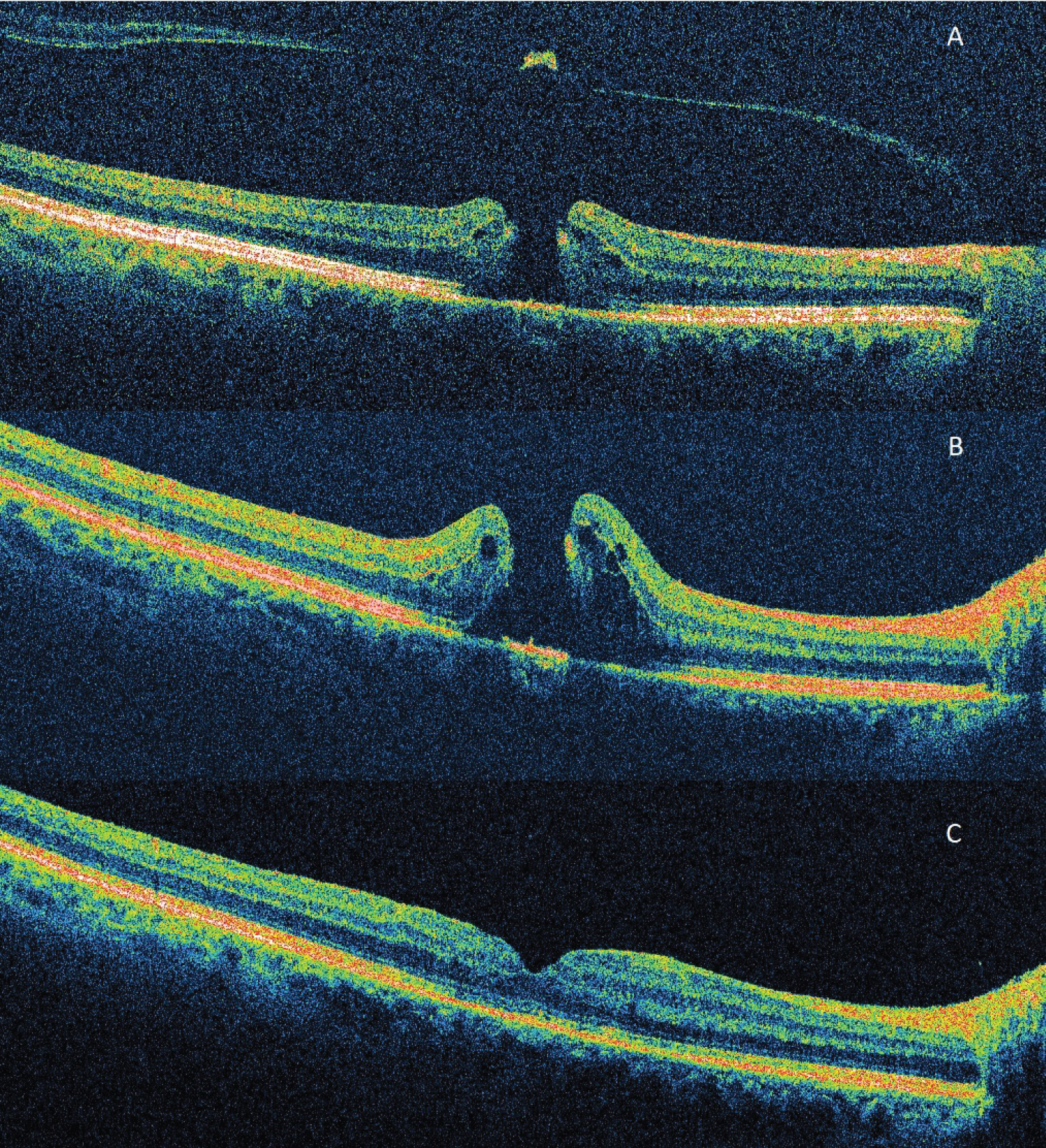
Analysis of the 10 unsuccessful MH (fMH) eyes show duration was 13 (± 6) months, 8 were large MHs and 2 were of medium size. For the large fMHs (n = 8) the complexity changed from a mean preoperative complexity score of 205 (± 16), increasing to 290 (± 31) postoperatively (at failed closure). When these eyes then underwent successful redo surgery the complexity scores reduced to 17 (± 9). The large fMHs had a greater preoperative complexity score (205) than the large MHs in eyes successfully closing with primary surgery (169) (p = 0.02). Duration fMHs13 (± 6) vs. MH (L) 10 (± 9) was not statistically significant (p = 0.20). The remaining cases of unsuccessful primary surgery were in medium sized MH. In one case the operating surgeon had performed a limited ILM peel at the first procedure under local anesthesia due to poor patient cooperation. The complexity was 39 preoperatively; it increased to 130 postoperatively at fMH with an open hole. After redo surgery under general anaesthesia, and a successful outcome, the complexity dropped to 17. Figure 4 shows the sequence of OCT macular morphology in this eye. In the other fMH of medium size, the preoperative complexity score was 140 and post-operatively increased to 166, before dropping to 16 after redo surgery.

For the unaffected fellow eye (UF), complexity was 15 (± 3) for S (UF), 31 (± 11) for M (UF), and 13 (± 3) for L (UF). Regarding PVD stage, 80 UF eyes were available for analysis: 70% (n = 56) had stage 3 PVD, and the remainder 30% (n = 24) had stage 1 PVD. The stage of PVD was not associated with the complexity scores (p = 0.23).

Discussion

Mathematical equations provide real physical parameters of the data source. The novel application used in our study provides a means of representing and further quantifying the anecdotal descriptions of 'complex' MHs. Some of the descriptions encountered by the authors for complex holes include the "square-edged hole", "rutting slugs" [6], "very large hole" etc. Although clinically appealing, these descriptions are not generalizable. We have utilized the software program Eureqa to analyze these unique mathematical relationships from an analogue of the MH geometrical shapes and configuration. GetData Graph Digitizer and Eureqa have been validated in scientific studies. GetData Graph Digitilizer is listed in the Cochrane Handbook for Systematic Reviews of Interventions as a tool for extracting data from figures [7].

Studies looking at foveal morphology in eyes subsequently developing MHs (termed premacular hole in the study) versus controls have shown no difference in the slope configuration between the eyes when PVD was present or absent. In a study looking at foveal morphology and the subsequent development of a MH, 43% of patients with a PVD went on to develop a MH [1]. It is interesting to note this high rate of MH formation in eyes with an established PVD. In our study, we have further quantified the stage of PVD and found that only 30% of UF eyes had a stage 1 PVD. These findings suggest that a complex relationship of forces exist on the retina, allowing MH progression despite resolution of the initiating tractional force. These forces are likely not merely in the anteroposterior and tangential directions, but also circumferential in nature.

Other studies have looked at 'normal' foveal morphology and changes with increasing age. The foveal anatomy was found to change with age, with normal aged foveae being less symmetric and having significantly steeper slopes, but with no significant difference in the foveal volume as compared to younger foveae. There was also a trend toward more complexity with ageing in the same study [8]. Furthermore, another study showed a significant difference between normal foveal configurations and premacular hole configurations. Foveal symmetry was also noted more in the normal foveae, as opposed to those developing MHs [9]. These studies illustrate the complex relationship occurring at the fovea before MH formation.

Studies looking at foveal anatomy of fellow eyes from patients with a history of MH showed 13% of patients have an irregular foveal contour with steep foveal slopes and a flat, wide fovea. Such abnormal foveal configurations are thought to represent early tangential traction. No evidence of VMT being associated with this irregular contour was found [10]. Although it was concluded that these results suggest OCT findings are a good predictor of subsequent MH formation, this is likely oversimplified, as there remains the question of why MHs progress even after an apparent complete PVD.

Our study is the first to utilize two powerful computer software programs to generate a complexity score for MHs. In our study, a surprising finding was the strong correlation between the preoperative BCVA and the preoperative MH complexity. This finding was not replicated between the BCVA and the MH stage. Another finding was no association between the duration of MH and the complexity. We found that the complexity scores also increased with increasing MH stage. Our findings suggest that complexity measurements are an indirect assessment of the stresses, exposure and subsequent dysfunction the macular components are undergoing, and hence the strong relationship between the BCVA and the complexity score.

Peeling of the ILM has been the subject of numerous studies. Recently, questions have been asked about the necessity of ILM peel for smaller hole closure. A Cochrane review of trials without OCT measurements, concluded that the available evidence supported ILM peeling in stages 2, 3, and 4 idiopathic MHs [11]. Another study found a 100% success rate for smaller holes (< 400 microns) [12]. Our case of the MH which required further surgery after incomplete ILM peeling illustrates that the level of complexity increased after the first failed surgery, with the OCT images correspondingly showing foveal asymmetry. After the successful repeat MH surgery, the complexity score reduced significantly. In the other fMHs, primarily large, failed surgery resulted in a higher complexity score, which reduced substantially with subsequent successful redo surgery. This might represent why it is crucial to perform a peel in medium - large MHs. Poor ILM peeling, where the ILM is removed partially, can result in an uneven force and contraction, which keep the MH open. It is therefore advisable to maintain the teaching of performing a peel circumferentially around the MH to avoid this uneven distribution of force. Unsuccessful large MH primary surgery eyes had higher complexity scores preoperatively than the lower scores noted in the eyes that underwent successful primary surgery. Whether this difference is due to the morphology, hence MH complexity and subsequent anatomical changes requires further studies. We have found that fMHs had higher complexity scores than the respective successful MH eyes. This warrants further investigation with a larger study and could help potentially identify MH surgery more prone to failure.

Our study excluded MHs from other causes, as well as patients with macular pathology disturbing the architecture of the OCT scan, such as macular atrophy, macular scar, pigment epithelial detachments, posterior staphyloma or other macular pathology likely to make the analysis unreliable. Also, no patients in the study had a refractive error greater than 3.00 dioptres. Therefore, our results may not be generalizable to MHs from other causes or eye with high refractive errors. Other weaknesses of the study include its retrospective manner. We also only analyzed the contour on single foveal OCT scans from the geometric center of the MH. Nonetheless, the complexity scores were consistent for MH stage.

Future studies will aim to apply the complexity scores to clinical findings, for example, visual function. We also plan to evaluate if this methodology can be used to distinguish full thickness MHs from lamellar or pseudo-holes. Complexity scores as a means of detecting foveal or macular anomalies should also be explored. Additionally, these findings might aid in the development or refinement of automated and/or artificial intelligence platforms to screen for macular pathology on OCT scans.

Declaration of Interest

The authors report no conflicts of interest.

No funding was received for this study.

References

1. Gaudric A, Haouchine B, Massin P, et al. (1999) Macular hole Formation: new data provided by optical coherence tomography. Arch Ophthalmol 117: 744-751.
2. Johnson MW (2005) Perifoveal vitreous detachment and its macular complications. Trans Am Ophthalmol Soc 103: 537-567.
3. Duker JS, Kaiser PK, Binder S, et al. (2013) The International Vitreomacular Traction Study Group classification of vitreomacular adhesion, traction, and macular hole. Ophthalmology 120: 2611-2619.
4. Schmidt M, Lipson H (2009) Distilling free-form natural laws from experimental data. Science 324: 81-85.
5. Schmidt M, Lipson H (2014) Eureqa (version 0.98 beta).
6. McPherson R (2015) Personal communication.
7. Higgins JPT, Thomas J, Chandler J, et al. (2019) Collecting data. In: Cochrane handbook for systematic reviews of interventions version 6.0. Cochrane.
8. Nesmith B, Gupta A, Strange T, et al. (2014) Mathematical analysis of the normal anatomy of the aging fovea. Invest Ophthalmol Vis Sci 55: 5962-5966.
9. Barak Y, Sherman MP, Schaal S (2011) Mathematical analysis of specific anatomic foveal configurations predisposing to the formation of macular holes. Invest Ophthalmol Vis Sci 52: 8266-8270.
10. Michalewska Z, Michalewski J, Sikorski BL, et al. (2009) A study of macular hole formation by serial spectral optical coherence tomography. Clin Exp Ophthalmol 37: 373-383.
11. Cornish KS, Lois N, Scott N, et al. (2013) Vitrectomy with internal limiting membrane (ILM) peeling versus vitrectomy with no peeling for idiopathic full-thickness macular hole (FTMH). Ophthalmology 121: 649-655.
12. Tadayoni R, Gaudric A, Haouchine B, et al. (2006) Relationship between macular hole size and the potential benefit of internal limiting membrane peeling. Br J Ophthalmol 90: 1239-1241.