Multidimensional Chaotic Dynamics and Entropies
In Search of Hidden Dimensions
The possible presence of further dimensions hidden in our three-dimensional-plus time world might help to elucidate countless physical and biological systems’ behaviors, from quantum entanglement to brain function. Nevertheless, suggestions concerning multidimensional arrangement of physical and biological systems do not deserve the role of scientific claims, unless the suggested additional dimensions can be verified via empirically testable hypotheses and experimental apparatus. Here we suggest that the widespread nonlinear dynamics and chaotic behavior of physical and biological collective systems might mirror further dimensions hidden in our world. Indeed, bringing together disparate knowledge from seemingly unrelated fields (brane cosmology, fluid dynamics, algebraic topology, computational topology, dynamic systems theory, logic and statistical mechanics), we show how, in logistic maps derived from nonlinear dynamical equations, the typical bifurcation diagrams might arise from linear flow paths, that intersect large-sized hidden dimensions at the canonical phase parameter’s values between three and four. Therefore, chaotic dynamics suggests the existence of a further hidden dimension in our Universe. We also provide a thermodynamic framework which suggests that the cosmic entropy is encompassed in a multidimensional manifold.
Introduction
In brane cosmology, strings and branes theories are based on the hypothetical existence of hidden dimensions surrounding us [1-3]. Our Universe could either lie on a spatial three-dimensional brane embedded in a higher dimensional bulk, or could be flanked by one or more multi-dimensional branes of different possible sizes and shapes [4,5]. Nothing is known about the scale of such extra dimensions. There is no consensus among theoreticians: some believe that extra-dimensions are warped in microns-scale manifolds, while others suggest that they could be of the size of millimeters, or hypothesize an indeterminately high hidden dimension surrounding us [6-8]. In order to assess the issue, we start from a recently proposed topological model, which suggests that two particles entangled in an n-dimensional space are un-entangled, when assessed in one dimension higher [9]. Because quantum entanglement occurs also between particles light-years away from each other, this means that, if their disentanglement occurs onto a further hidden dimension, the extra-dimensional manifolds must be very large and must influence also our three-dimensional-plus time (space-time) Universe. This observation points towards elusive higher dimensions surrounding us, able to intersect our space-time world and to interact with it. Such invisible (e.g., hidden by our standpoint of observers embedded in a space-time structure), infinite curvilinear dimension(s) crosses and/or is embedded in the fabric of our world. In order to try to elucidate our rather speculative claim, we look for hints of hidden dimensions in natural phenomena occurring in our space-time world, starting from the premise that extra-dimensions might be emergent also in our lower-dimensional environment.
In particular, we evaluate the widespread complex, nonlinear physical and biological collective systems, equipped with non-equilibrium dynamics and characterized by a large number of interacting and inter-dependent components, spontaneous self-organization and self-organized criticality [10-14]. Many physical and biological collective nonlinear systems operate at the edge of chaos. A chaotic system displays dependence from initial conditions, positive Lyapunov exponents and attractors. They tend to live near a metastable state of second-phase transitions, characterized by infinite correlation length, countless functional dimensions [15], spontaneous avalanches and universal power laws [16-18].
Here we show, based on claims from far-flung disciplines that the typical bifurcation diagram of logistic maps’ nonlinear dynamical equations might arise from the interaction of linear paths with large-sized hidden dimensions intersecting them. We introduce a multidimensional approach that offers an explanation of some aspects of dynamic systems theory, in particular Hopf bifurcations, in terms of hidden dimensions, and also a method in order to evaluate the consequences of this strategy. We also provide a framework able to solve a long-standing issue. Indeed, the second law of thermodynamics states that the thermodynamic entropy tends to increase in a closed system, so that the process is irreversible. We asked: why is thermodynamic entropy frequently unchanged, during nonlinear phase transitions?
Materials and Methods
In order to assess and operationalize our hypothesis that hidden dimensions, endowed in our space-time world, might give rise chaotic nonlinear dynamics, we need to develop the proper procedures. In search for hidden dimensions, we will proceed as follows: at first, we will provide a brief description of logistic plots. Then, we will describe four different approaches from far-flung disciplines. We will try to demonstrate that they stand for different clues converging towards our claim.
Premise: Chaotic bifurcations and logistic plots
As stated above, different physical and biological systems display nonlinear features. This form of dynamics is frequently studied through logistic maps equipped with bifurcations, which intervals are dictated by the Feigenbaum constants [19]. A logistic map is a one-dimensional nonlinear difference equation, widely used to study dynamic systems theory’s issues [20]. It encompasses a generic variable representing an observable behavior and a fixed behavioral parameter (the phase parameter). Logistic maps can be plotted and visualized on a one-parameter bifurcation diagram, as a function of the scaled parameter r. Note that, at the edge of criticality, bifurcations occur.
The first universal Feigenbaum constant stands for the limiting ratio of each bifurcation interval to the next, between every period doubling [21]. It is applicable to one-parameter maps, where f(x) is a function parameterized by the bifurcation parameter a:
and also for other logistic maps, such as:
and
Therefore, every chaotic system, described by maps with a single quadratic maximum, will bifurcate at the same rate, i.e., the first Feigenbaum constant [22]. The latter is a transcendental number, given by the limit [23]:
Where an stands for discrete values of the variable a at the nth period doubling. Note that the ratio converges to the first Feigenbaum constant.
The second Feigenbaum constant, i.e,
α = 2.502907875095892822283902873218…,
is the ratio between the width of a tine and the width of one of its two subtines (except the tine closest to the fold). A negative sign is applied to α, when the ratio between the lower subtine and the tine width is measured.
The first approach: Detecting dimensions through flows assessment
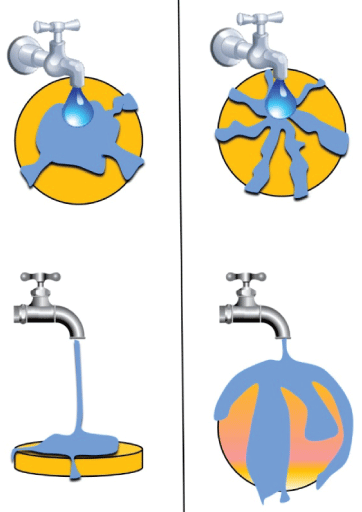
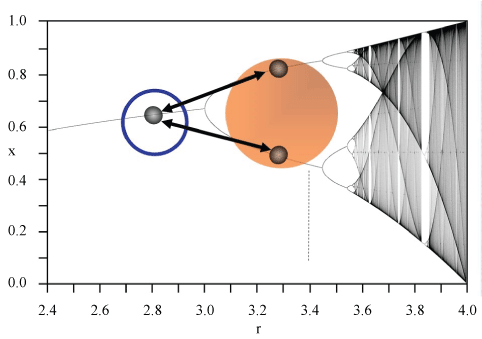
When you watch from afar a circular structure, you may not be sure if it is a 2D disk or a 3D sphere, unless you go close and look for shadows or angles. There is however an indirect procedure, in order to detect objects’ dimensions and shape. If you convey a laminar flux towards its surface, you can assess fluxes’ trajectories (Figure 1). Therefore, looking at flows’ behavior, you may assess whether the circular structure displays two or three dimensions. In other words, we are allowed to evaluate what happens to a water flow when we introduce a solid object that, being an interposed obstacle, is able to modify the liquid paths. For example, if you use a funnel, the water will be conveyed in a very thin flow.
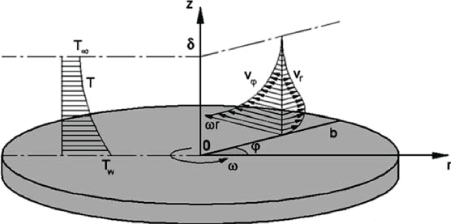
In Figure 2, for sake of simplicity, we described a water flow. Nevertheless, we are also allowed to use other kinds of streams, such as electromagnetic or sonic currents, and so on [24,25]. Every one of such fluxes obeys different types of well-established equations, following well-studied trajectories that could be visualized and quantified. For example, air fluxes on a disk have been widely investigated. The flux features will tell us about the shape of the hidden surface. Indeed, by knowing the disk’s radius and the strength of the uniform field, we may evaluate the orientation and movements of the disk’s surface and the presence of hidden obstacles (Figure 2), both for laminar or turbulent fluxes. As an example of previously unrecognized classes of flows, stochastic heat engines have been assessed, in particular a colloidal sphere diffusing in a conventional optical tweezer [26]. In this case, non-conservative optical forces bias the particle’s fluctuations into toroidal vortexes, whose circulation can reverse direction with temperature or laser power.
These methods from fluid dynamics allows us to look (in physical and biological systems’ phase spaces with superimposed “obstacles” to the flux) for hypothetical traces left by different kinds of fluxes, in order to indirectly assess possible hidden dimensions and their shapes. In particular, we might be able to assess what happens to a particle trajectory traveling in a n-spatial environment, when it interacts with an object not endowed in a further spatial dimension, but instead endowed in an abstract “super space” [27]. Super spaces have been introduced in the study of super symmetry, in order to compare the otherwise not assessable bosons and fermions’ total behavior. The philosophy behind super spaces is to embed phase spaces both in spatial and non-spatial dimensions, in order to improve the detectability of otherwise invisible parameters. Here we use super spaces in guise of abstract, non-spatial dimensions superimposed to spatial systems, able to interfere with the trajectories occurring in classical spatial n-dimensions.
The second approach: Topology comes into play
The Borsuk-Ulam Theorem (BUT) states that, if a sphere Sn is mapped continuously into an n-dimensional Euclidean space Rn, there is at least one pair of antipodal points on Sn which map onto the same point of Rn [28,29]. See Tozzi and Peters [30] for further details and a mathematical treatment. The notation stands for an n-sphere [31], which is an n-dimensional, circular structure, embedded in an n + 1 space [32]. For example, a 2-sphere (S2) is the 2-dimensional surface of a 3-dimensional space. Antipodal points are, e.g., the poles of a sphere [33,34].
Several BUT variants have been developed in the very last years. For example, we can consider regions on an n-sphere that are either adjacent or far apart. This means that pairs of points need not be antipodal, in order to have matching descriptions [35]. This BUT variant has utility, provided there are a pair of regions on an n-sphere which are similar. The concept of antipodal points can be used not just for the description of points, but also for more complicated structures, such as shapes of space (object contours), temporal intervals (temporal oscillations), functions, vectors and symmetries [36,37]. This leads to a particularly useful region-based BUT, dubbed re-BUT [35]. We are allowed to describe brain features on an n-sphere either as antipodal points, or antipodal regions. This means that antipodal signal shapes can be compared [35]. That is, feature-based descriptions of antipodes can be assessed at one level of observation, while their projections into a single shape can be analyzed at a lower level [37].
Although BUT was originally limited to an n-sphere where n is a natural number, nevertheless n can also be regarded as rational or irrational number [37]. For example, we might regard functions or shapes as embedded in a sphere in which n stands for number of instants in time. Hence, the parameter n becomes useful in the description of nonlinear and fractal dynamical systems.
The original formulation of BUT describes the presence of antipodal points on spatial manifolds in every dimension, provided the manifold is a convex, positive-curvature structure (e.g., a ball). However, the kind of geometry that best describes world dynamics is a matter of debate. Theoretical contenders include Euclidean, elliptic and hyperbolic geometry. This means that systems functions might occur on manifolds endowed with different types of geometry, for example the hyperbolic one encloses complete Riemannian n-manifolds of constant sectional curvature-1 and concave shape [38]. We are thus allowed to look for antipodal points also on structures equipped with kinds of curvature other than the convex one [39]. Or, in other words, whether the system under examination displays a concave, convex or flat functional appearance, it does not matter: we may always find the points with matching description predicted by BUT. For further details, see also Peters and Tozzi [37].
In sum, the BUT displays versatile features which can be modified in different guises: last but not least, the mapping of antipodal points into the lower level of a n - 1 sphere. In our case, we are allowed to use BUT in order to describe Hopf bifurcations, because the latter cannot occur in discrete-time systems or maps. However, because the intended meaning is related to a Poincare section, the argument about the hidden dimensions holds true. Precisely, a period-doubling bifurcation in the logistic map may correspond to a double-covering bifurcation of a limit-cycle in a higher dimensional space.
The third approach: Computerized tessellation of the image of the logistic plot
We assessed the logistic plot “classical” image of nonlinear, chaotic dynamics through a novel image analysis approach [40,41]. Indeed Peters, et al. [41] introduced a novel method for the measurement of information level in data sets, based on image subdivision in small polygons equipped with different entropic content. This method, called maximal nucleus clustering, is based on nucleus clustering in Voronoï tessellations [42]. In brief, a computerized program chooses the points of the image with the higher difference of orientation, compared with the others. The choice of such points, called generating points, allows us to build around them small polygons, called Voronoi tessellation regions. Such small polygons, depending on the number of their sides, display different levels of information. In particular, the polygons with the higher number of sides, called Maximum Nucleus Clusters (MNC), together with their surrounding polygons, might be an indirect clue of hidden dimensions in a two-dimensional Figure. Indeed, MNC reveals zones of the image characterized by different gradient orientation and diverse functional dimensions [40]. The fractal structure of the logistic map is believed to come from the stretch-and-fold process: therefore, why, in our framework, do MNCs imply hidden dimensions? In Peters, et al. [40] we hypothesized that every parameter correlated with the MNCs might stand for a functional dimension. In the previous paragraph, we introduced the concept of BUT and matching signals. The basic form of BUT tells us that there exists a pair of antipodal (opposite) signals on the circumference that maps to a single one on a line. The two antipodal signals are assessed at one level of observation, while the single one at a lower level. This means that, if we embed a MCN onto a circumference, there exist two antipodal signals with matching description. Therefore, BUT provides a handy vehicle in expressing the relationship between Voronoï polygons that serve as cluster nuclei. In the image tiling, more than one MCN can be found, all of them equipped with the same number of sides (i.e., these MCNs display matching description). Therefore, different MNCs may be embedded in the same circumference and may display matching functional description. In other words, systems features could be characterized as antipodal signals with matching description, in order that the functions of signal shapes can be compared. It might be speculated that changes in morphological features could be correlated with variations in physical functions. Thus, gradient differences might be linked with different functional and dimensional counterparts.
Although we live in a space-time world with no immediate perception that hidden spaces exists at all, the hints of a further dimension can be identified through their “cross section” movements on a more accessible three-dimensional surface, as if you recognized some object from its shadow projected on a screen. In such a vein, MNCs might be able to evaluate indirect clues of the undetectable fourth dimension, e.g., the hallmarks or signs on a familiar space-time surface.
The fourth approach: Logical validation
Here we asked whether it is feasible to validate as true, through logic tools, the possibility that a logistic plot is correlated with a hidden dimension that intersects linear behaviors of collective systems, when they phase parameter changes from 3 to 4. In general terms, we described a logical question in the format of: “if possibly A (with its logical parts), then B” to be validated true or validated not true. In our specific case, we asked whether the following two questions are logically tenable:
a) Is it possible that laminar fluxes can be unobstructed or bifurcated by interposition of the necessity of hidden dimensions implying visible dimensions?
b) The necessity of non-visible dimensions imply the possibility of laminar fluxes as either: 1) Not obstructed; or 2) Bifurcated by non-visible dimensions implying visible dimensions?
We used the following logic procedure. We mapped categorical subject parts into “literal” variables. The validation was performed by the logic model checker Meth8 (U.S. Patent pending). Meth8 is a logic model checker which requires each expression as a numbered equation to be validated true/not validated true in each case to constitute a well-formed and satisfiable proof. It is based on VŁ4, the variant that corrects and resuscitates the quaternary logic Ł4 of Łukasiewicz.
We used the 4 propositions < p, q, r, s >. We mapped action relations into respective lists for:
a) Connectives < And; Not and; Or; Not or; Equivalent; Not equivalent; Imply; Not imply >;
b) Common symbols with ~ for Not as the set { &, ~&, V, ~V, ↔, [ ], →, ← } ;
c) One letter symbols in Meth8 as the set { & , \ , + , - , = , @ , > , < }.
We also mapped modifiers in modal operators for possibility and necessity, using the following symbols:
a) Common symbols of the lozenge ◊ and box [];
b) One letter characters in Meth8 as % and #.
Predicate logic has two quantifiers, the existential ∃ as “at least one exists” and the universal ∀ as “for all”. The quantifiers are based on (the misattributed) Aristotle’s Square of Opposition which provably is not bivalent (not exact).
However, propositional logic has two modal operators that provably are bivalent (exact) and generally interchange with the two quantifiers, ◊ for ∃ and [] for ∀.
We also mapped expressions into the format of:
a) Named types in order of literal, operator, literal such as p & q;
b) Named parts in order of antecedent, connective, consequent.
Results
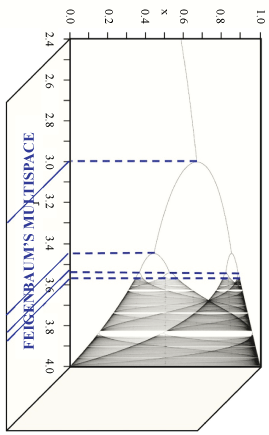
Here we show how the bifurcation diagram of 2D logistic maps’ nonlinear dynamical equations might be shaped and deformed by an intersecting hidden dimension, e.g., a super space containing the first Feigenbaum constant.
The first approach: Detecting dimensions through flows assessment
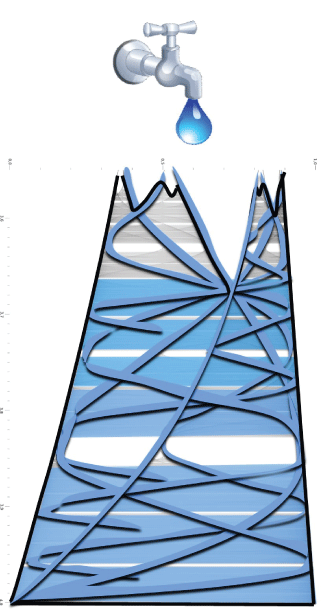
In this logistic plot, x stands for the detectable trajectory followed by a particle in a space-time, and r stands for possible hidden dimensions. When the scaled parameter r is measured between 1 and 3, the particle behavior is linear. When the value 3 is reached, it looks like an obstacle to the flow occurs (Figure 3). At phase parameter’s values between 3 and 4, the super space (e.g., one or more hidden dimensions) interferes with the plot and interacts with the traveling particles. When linear trajectories cross the super space, they split into progressively increasing fractal bifurcations, until a totally chaotic pattern is achieved. Interestingly, this further dimension(s) is somewhat correlated with the first Feigenbaum constant (Figure 4).
The second approach: Topology comes into play
Tozzi and Peters [30] demonstrated that embracing systems non-linearity in the framework of the Borsuk-Ulam theorem means that nervous bifurcation transformations (the antipodal points) can be described as paths or trajectories on abstract spheres equipped with Feigenbaum dimensions (Figure 5). Note that, from linearity to non-linearity, the number of points with matching description increases. This means, for the BUT theorem and its variants, that, going from phase parameter 3 to 4, it occurs an increase of n-dimensions. However, in this case, the term n does not stand for a natural number as in the classic BUT, but for an irrational number (the Feigenbaum constant). We could state that, in a logistic plot equipped with a hypothetical hidden dimension, the increase of bifurcations is given by the BUT dictates (e.g., a single feature in n-dimensions maps to two features or more in n + 1 dimensions). The concave trajectories are caused by the shape of the hidden dimension(s), because the bifurcation distortion could be due to a negative-curvature superimposed manifold(s). There must be a concave manifold that modifies the original linear curve, when, at the proper values of the phase parameter, trajectories pass through it. In sum, chaotic behavior might be correlated with the intersection between the linear path and a hidden dimension(s).
The third approach: Computerized tessellation of the image of the logistic plot
Figure 6 depicts MNCs in a tessellated logistic plot at different magnifications. Note that in this case MNCs and their surrounding polygons stand for the possible location of the hidden dimension interfering with linear trajectories.
The fourth approach: Logical validation
Our first question was:
“Is it possible that laminar fluxes can be unobstructed or bifurcated by interposition of the necessity of hidden dimensions implying visible dimensions?”
(Q1)
LET:
p = dimensions; q = visibility; r = fluxes; s = laminar; ~ Not (negation);
% possibility; # necessity;
> Imply; < Not Imply; = Equivalent; @ Not Equivalent; + Or; & And;
(p@p) False (obstructed); ~(p@p) = (p = p) True (unobstructed); vt Validated true true.
Our second question was:
“Does the necessity of non-visible dimensions imply the possibility of laminar fluxes in Eq Q1 as either: 1. Not obstructed; or 2. Bifurcated by non-visible dimensions implying visible dimensions?”
(Q2)
#(p&~q) > %(((r&s) > ~(p@p)) + ((r&s) > ((p&~q) > (p&q)))); vt
Model 1 TTTTTTTTTTTTTTTT
Model 2.1 EEEEEEEEEEEEEEEE
Model 2.2 EEEEEEEEEEEEEEEE
Model 2.3.1 EEEEEEEEEEEEEEEE
Model 2.3.2 EEEEEEEEEEEEEEEE
The answer to the two questions is "yes", as proved by the truth table for Q1 with Q2 in Model 1.1.
In sum, we indirectly suggested, summoning clues from completely different approaches, the presence of an invisible, extra-large dimension intertwined with our space-time world and able to interact with it.
Conclusions
Claims from theoretical physics and, recently, also from neuroscience [30], suggest the possible presence of extra dimensions interacting with our three-dimensional-plus time physical and biological world. It has been hypothesized that elusive, higher dimensions of unknown curvature (either flat, or curved, or warped, and so on) surround us, intersecting our space-time world and interacting with it. Our aim was to propose a method in order to detect such hidden dimensions. We showed how their presence can be proofed by the occurrence of bifurcations, while their shape can be extrapolated from the curves’ deformation after every bifurcation. In particular, in logistic plots from nonlinear chaotic collective dynamics, we showed how it is possible to detect the hints of an unknown factor, able to vary the otherwise linear particle trajectories. The interaction between the usual space-time trajectories and the further dimension(s) occurs just when the proper angles allow their superimposition. Therefore, we find trajectory divergences that are detectable in our world.
Due to the current lack of knowledge, we were not able to elucidate the features of such a hidden dimension. Although we stated that possible hidden dimensions interfere with physical and biological processes, giving rise to nonlinear dynamics in our world, nevertheless we never talked about the nature of such dimension and about “spatial” features. Indeed, we are not allowed to say whether we are in front of one, or more than one, further spatial dimension. The concave shape of trajectories could also be provided by the curvature of a complex (real and imaginary) space, that displays, in a physical geometry, a dual mapping between: a) Visible regions embedded in an n dimensional real space and b) Hidden regions mapping to an n + 1 - dimensional imaginary space. Another possibility is that the hidden dimension stands for a “temporal” dimension, instead of a spatial one. Due to our above described quantum entanglement account; we might speculate that (in our space-time, zero curvature Universe) a further hidden, infinite dimension is endowed, in guise of an invisible rolled, tangled thread, or wire. We might hypothesize that a sort of one-dimensional rope surrounds us. Differently from other models that suggest particles trajectories travelling along different dimensions of a multidimensional phase space, we propose that particles move into our space-time phase space, but collide with such one-dimensional rope endowed in the cosmos. A one-dimensional rope cannot encompass a two-dimensional oscillation, but just a uni-dimensional force. Nevertheless, if such hypothetical one-dimensional force propagates into our space time cosmic dimensions, it would give rise to pluri-dimensional oscillations detectable by us. Which kind of force can be encompassed in a mono-dimensional rope? If we hypothesize that this dimension is made of negative time (an inverted arrow of our usual time), we solve a lot of puzzling experimental observations, with no need to further, problematic forces.
Is also feasible that the hidden dimension has something to do with the Feigenbaum constant, e.g., with an irrational number. In such a speculative vein, we need to remember an astonishing, unnoticed similarity between the numbers of the first Feigenbaum constant and the Zeeman Effect, which is correlated with magnetic fields. Indeed, the value of Zeeman Effect’s constant is 4.66860 × 101 metre/tesla, a value that parallels the first four numbers of the first Feigenbaum constant, in particular for the highest values of bifurcations in logistic plots. Of course, caution is needed, for two reasons: a) We did not assess standard deviation or correlation statistic to show the corresponding similarity; b) The Zeeman constant depends on the arbitrary chosen unit system, while the Feigenbaum constant is a ratio; therefore, it could simply mean that such concurrence is purely random. Nevertheless, the coincidence is remarkable, and might point towards a hypothetical correlation between two widespread features of our world: nonlinear chaotic bifurcations and magnetic fields.
The phase transitions described in chaotic nonlinear logistic plot do not lead to changes in thermodynamic entropy. Our framework helps to better elucidate such issue, by providing a multidimensional account of thermodynamic entropy able to elucidate the second law of thermodynamics and to answer to a long-standing question: why does the thermodynamic entropy increase in our three-dimensional (plus time) Universe? Where the increase of entropy does comes from? Here the Bekenstein inequality comes into play. Let k be Boltzmann’s constant, R the radius of a sphere that can encompass a given system, E the total mass energy (including any rest masses), ħ the reduced Planck constant and c the speed of light. The Bekenstein bound is an upper limit on the entropy S (or information I) encompassed into a finite region of space equipped with a finite amount of energy. In other words, the Bekenstein bound stands for the maximum amount of information required to describe a physical system down to the quantum level. This means that the information of a physical system, or the information necessary to describe it, must be finite, in case of both the region of space and the energy being finite. The universal form of the bound can be described as follows [43,44]: , Where f is the wave frequency of the particulate photon energy E and h is the quantum of action (Planck’s constant).
A noteworthy consequence of the Berkenstein bound, i.e., that the entropy contained in our space-time Universe is proportional to the two-dimensional border of the sphere enclosing the system, led some theoreticians to hypothesize the holographic principle. The latter states that the entire universe can be seen as two-dimensional information on the cosmological horizon, such that the three dimensions (plus time) we observe are an effective description only at macroscopic scales and low energies. The holographic principle was inspired by black hole thermodynamics, which conjectures that the maximal entropy in any region scales with the radius squared, and not cubed as might be expected. Indeed, the Bekenstein-Hawking formula states that the black hole entropy is proportional to the area of its event horizon. The fact that the black hole entropy is also the maximal entropy that can be obtained by the Bekenstein bound (wherein the Bekenstein bound becomes equality) was the main observation that led to the holographic principle. Summarizing, the holographic model hypothesizes that the entropy endowed in our space-time Universe might be encompassed in a two-dimensional surface, because, in the case of a black hole, the informational content of the objects fallen into the hole might be entirely contained in surface fluctuations of the event horizon. Our goal is to “reverse” such idea: if we place a three-dimensional sphere instead of a two-dimensional one on the right side of the equation, we achieve on the left side the value of the entropy encompassed in FOUR dimensions. Put another way, the Bekenstein bound is the upper limit of the energy of a system at a particular time t defined by
Therefore, if we achieve thermodynamic entropy encompassed in a multidimensional Universe instead of the space-time one, we are able to explain why the entropy S seems to increase in our detectable Universe’s linear paths, while it is kept invariant during nonlinear chaotic phase transitions. Indeed, if we keep the Universe enthalpy constant, we might hypothesize that the free-energy flows towards the further dimension, leaving in our space-time dimensions an apparent, relative increase in entropy. Therefore, free energy is “sucked” by, “drained” towards the hidden dimension. This apparent phenomenon disappears at the observation level of a higher dimension, where the entropy is left unchanged: this is the case of the logistic plot after bifurcations and of an hypothetical thermodynamic entropy embedded in a further, hidden dimension.
Our findings pave the way to future works and developments. Further mathematical studies are needed, in order to assess the shape of the hidden dimension(s). Our procedure allows not just to look for hints of veiled dimensions in our microscopic or macroscopic Universe, but also to use abstract dimensions in order to evaluate natural paths. Although we took into account the example of the Feigenbaum multi space, we can also use other multi spaces, e.g., dimensions containing physical constants, in order to evaluate happens when a dynamic system interferes with such dimensions. Furthermore, by measuring the curvature of laminar fluxes when they approach cosmic bodies, we could study solar winds, electromagnetic waves or cosmic wave’s background, in order to assess whether hidden dimensions are endowed in our Universe, and where they are located.
References
- Rubakov VA, Shaposhnikov ME (1983) Do we live inside a domain wall? Physics Letters B 125: 136-138.
- Baulieu L, Green M, Picco M, et al. (2001) Progress in String Theory and M-Theory. Springer, Berlin.
- Hashimoto K (2012) D-Brane: Superstrings and New Perspective of Our World. Springer-Verlag, Berlin.
- Hitchin N (2003) Generalized Calabi-Yau manifolds. The Quarterly Journal of Mathematics 54: 281-308.
- Burgess CP, van Nierop L (2013) Technically natural cosmological constant from supersymmetric 6D brane backreaction. Physics of the Dark Universe 2: 1-16.
- Candelas P, Horowitz G, Strominger A, et al. (1985) Vacuum configurations for superstrings. Nuclear Physics B 258: 46-74.
- Arkani-Hamed N, Dimopoulos S, Dvalic G (1998) The hierarchy problem and new dimensions at a millimeter. Physics Letters B 429: 263-272.
- Randall L, Sundrum R (1999) A Large Mass Hierarchy from a Small Extra Dimension. Physical Review Letters 83.
- Peters JF, Tozzi A (2016) Quantum Entanglement on a Hypersphere. Int J Theoret Phys 55: 3689-3696.
- Bak P, Tang C, Wiesenfeld K (1987) Self-organized criticality: An explanation of the 1/f noise. Phys Rev Lett 59: 381-384.
- Fraiman D, Chialvo DR (2012) What kind of noise is brain noise: Anomalous scaling behavior of the resting brain activity fluctuations. Front Physiol.
- Perkins TJ, Foxall E, Glass L, et al. (2014) A scaling law for random walks on networks. Nat Commun 5: 5121.
- Deco G, Jirsa VK (2012) Ongoing cortical activity at rest: criticality, multistability, and ghost attractors. J Neurosci 32: 3366-3375.
- Tozzi A (2014) Evolution: Networks and Energy Count. Nature 515: 343.
- Afraimovich V, Tristan I, Varona P, et al. (2013) Transient Dynamics in Complex Systems: Heteroclinic Sequences with Multidimensional Unstable Manifolds. Discontinuity, Nonlinearity and Complexity 2: 21-41.
- de Arcangelis L, Herrmann HJ (2010) Learning as a phenomenon occurring in a critical state. Proceedings of the National Academy of Sciences 107: 3977-3981.
- Beggs JM, Timme N (2012) Being critical of criticality in the brain. Front Physiol 3: 163.
- Tozzi A (2015) How to Turn an Oscillation in a Pink One. Journal of Theoretical Biology 377: 117-118.
- Strogatz SH (1994) Nonlinear Dynamics and Chaos, Studies in Nonlinearity. Perseus Books Publishing.
- Richardson MJ, Dale R, Marsh KL (2014) Complex dynamical systems in social and personality psichology. In: Reis HT, Judd CM, (2nd edn), Handbook of Research Methods in Social and Personality Psychology. Cambridge University Press, Cambridge.
- Smith R (2013) Period doubling, information entropy, and estimates for Feigenbaum’s constants. International Journal of Bifurcation and Chaos 23.
- Alligood KT, Sauer TD, Yorke JA (1996) Chaos: An Introduction to Dynamical Systems. Textbooks in Mathematical Sciences, Springer.
- Jordan DW, Smith P (2007) Non-Linear Ordinary Differential Equations: Introduction for Scientists and Engineers. (4th edn), Oxford University Press.
- Reynolds O (1883) An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and the law of resistance in parallel channels. Philosophical Transactions of the Royal Society 174: 935-982.
- Tritton DJ (1988) Physical Fluid Dynamics. (2nd edn), Oxford University Press, UK.
- Sun B, Grier DG, Grosberg AY (2010) Minimal model for brownian vortexes. Phys Rev E Stat Nonlin Soft Matter Phys 82.
- Rogers A (2007) Supermanifolds: Theory and Applications. World Scientific.
- Borsuk K (1933) Drei satzeuber die n-dimensional euklidische sphare. Fundamenta Mathematicae 20: 177-190.
- Beyer WA, Zardecki A (2004) The early history of the ham sandwich theorem. American Mathematical Monthly 111: 58-61.
- Tozzi A, Peters JF (2016) Towards a Fourth Spatial Dimension of Brain Activity. Cognitive Neurodynamics 10: 189-199.
- Weeks JR (2002) The shape of space. (2nd edn), Marcel Dekker Inc, New York-Basel.
- Marsaglia G (1972) Choosing a Point from the Surface of a Sphere. Ann Math Statist 43: 645-646.
- Matousek J (2003) Using the Borsuk-Ulam Theorem. Lectures on Topological Methods in Combinatorics and Geometry. Springer-Verlag Berlin Heidelberg.
- Collins GP (2004) The shapes of space. 291: 94-103.
- Peters JF (2016) Computational Proximity: Excursions in the Topology of Digital Images. Intelligent Systems Reference Library 102.
- Borsuk K (1969) Fundamental retracts and extensions of fundamental sequences. Fundamenta Mathematicae 64: 55-85.
- Tozzi A, Peters JF (2016) A Topological Approach Unveils System Invariances and Broken Symmetries in the Brain. Journal of Neuroscience Research 94: 351-365.
- Sengupta B, Tozzi A, Cooray GK, et al. (2016) Towards a Neuronal Gauge Theory. PLoS Biol 14: e1002400.
- Mitroi-Symeonidis FC (2015) Convexity and sandwich theorems. European Journal of Research in Applied Sciences 1: 9-11.
- Peters JF, Tozzi A, Ramanna S (2016) Brain Tissue Tessellation Shows Absence of Canonical Microcircuits. Neuroscience Letters 626: 99-105.
- Peters JF, Ramanna S, Tozzi A, et al. (2017) BOLD-independent computational entropy assesses functional donut-like structures in brain fMRI image. Frontiers Hum Neurosci 11:38.
- Peters JF, Inan E (2016) Strongly near Voronoi nucleus clusters.
- Bekenstein JD (1973) Black Holes and Entropy. Phys Rev D 7: 2333-2346.
- Bekenstein JD (1974) Generalized second law of thermodynamics in black-hole physics. Phys Rev D 9: 3292-3300.
- Shevchuk IV (2009) Modelling of Fluid Flow and Heat Transfer in Rotating-Disk Systems. In: Convective Heat and Mass Transfer in Rotating Disk Systems. Lecture Notes in Applied and Computational Mechanics. Springer, Berlin, Heidelberg, 45: 11-31.
Corresponding Author
Arturo Tozzi, Center for Nonlinear Science, Department of Physics, University of North Texas, 1155 Union Circle, #311427, Denton, Texas 76203-5017, USA; Computational Intelligence Laboratory, University of Manitoba, Winnipeg, Winnipeg R3T 5V6 Manitoba, Canada.
Copyright
© 2017 Tozzi A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.