Exploration of Multiscale Geometric Analysis for Enhancement and Structure Detection in MRCP Images

Abstract

Magnetic Resonance Cholangiopancreatography (MRCP) images are used in the diagnosis and treatment planning of the bile ducts and the liver. The ability to diagnose and treat such diseases in recent times has increased with greater importance placed on the effective use of non-invasive medical imaging. However, MRCP images are often noisy (low signal-to-noise ratio) and suffer from the influence of artifacts, partial volume and large inter-image variations. This paper evaluates the suitability of several Multiscale Geometric Analysis (MGA) techniques, to improve the quality of the 2D MRCP images and enhance the detection of the biliary structures within them. Tests results, evaluated subjectively to correspond with the human visual perception, achieved promising results for contourlets, curvelets as well as a non-orthogonal wavelet noise compensation implementation. The findings may contribute to assist in the development of automatic computer-aided diagnosis systems for liver diseases affecting the bile ducts as well as in clinical diagnosis.

Keywords

Bile ducts, Liver diseases, Contourlet, Curvelet, Ridgelet, Non-othogonal wavelet

Introduction

MRCP or magnetic resonance cholangiopancreatography is the medical imaging modality used to visualize the pancreato-biliary structures in the abdomen [1]. The structures, commonly called the bile ducts or biliary tree, are responsible for the transportation of the bile from the liver to the gallbladder for storage, and ultimately to the small intestines where the bile is used in the digestion of fat-based vitamins and minerals. The bile, is also responsible for the absorption and removal of fat and oil-soluble waste products such as cholesterol from the body. Thus, diseases affecting the bile ducts, directly or indirectly (such as non-biliary liver diseases), often cause blockages to parts of the biliary structure which restrict the flow and in turn cause the build-up of bile and toxic waste matter in the liver and body. This leads to pain, swelling, potential organ failure, poisoning, malnutrition and various other complications.

MRCP is essentially a special sequence of MRI (magnetic resonance imaging). A typical MRCP examination may be conducted with or without a contrast medium, and consist of series of images totaling over a hundred individual MRCP images [2]. These include some MRI images in the axial and coronal or sagittal orientations for locating the region of interest (ROI), thick slab and thin slice MRCP images, all of which may be acquired using the T1- and/or T2-weighted sequences. For more accurate diagnosis, thinner slices would enable better visualization and reconstruction of the 3D volume, but the image quality (in terms of signal-to-noise ratio or SNR) deteriorates as the slice thickness is reduced. Even with thick slab images, where the point volume as thick as 50mm is represented as a single pixel in the 2D image, there is a significant amount of noise present in the image. Furthermore, MRCP images are also susceptible to acquisition artefacts, fat density of the patient, parameter settings, influence of other diseases (e.g. those affecting the liver), liver tissue and presence of other organs in the image (e.g. intestines, gallbladder, stomach), non-optimal acquisition orientation (where parts of the structure may be obstructed or misrepresented) and very large dynamic range of shapes, dimensions and intensities representing the various parts of the entire biliary tree.

MRCP images used in this study were acquired from a collaborating medical institution and from other institutions through the Internet. From observation (see later in the results section), there is a significant amount of differences present in the various images. Often, variations are not only observed for inter-hospital or inter-patient images, but even in inter- and intra-series images of the same patient. This is due to not just the anatomical disposition of the patient (e.g. body fat), but also the various sequences, parameter settings, series and orientations that a radiographer may use in order to obtain the "best" images for the diagnosis by the radiologist. Thus, the normalization step via pre-processing is essential for MRCP analysis and structure detection.

The problems listed above constitute the difficulties in developing automatic computer systems for the detection and diagnosis using MRCP images. The many classes of problems above require multi-stage processing in order to extract the relevant information and overcome the weaknesses present in the images. This paper reports on a study undertaken on the more fundamental aspect of those stages, namely the preliminary pre-processing for image denoising and enhancement of the biliary structures in the MRCP images. The objective of this work is to identify the techniques that produce good and reliable pre-processing for MRCP images, such that other subsequent algorithms may be applied more successfully to aid in the processing, detection and diagnosis of MRCP images either in the clinical environment or through the development of a computer-aided diagnosis (CAD) system for biliary diseases.

Methods

The term pre-processing encompasses any preliminary processing undertaken prior to the main task in achieving the set goal. Thus, depending on the intended goal, the tasks required in the pre-processing stage may range from minor image setting to extensive structure reconstruction and beyond. Image denoising typically consists of three steps: converting the image into another domain where the noise component is more obvious, thresholding the noise, and finally taking the inverse transform to return the resulting image into its original spatial domain. Wavelets [3], and the broader category of Multiscale Geometric Analysis (MGA) tools [4], have been found to be effective in distinguishing the data and noise components of the image signals. The scope of this work will be limited to enhancing of the MRCP images with the new generation high performance wavelets, such that the noise present may be minimized and the clarity of the significant bile duct structures maximized. This section will describe the popular multiresolution techniques undertaken in this work to evaluate their suitability for MRCP pre-processing.

Wavelets

Impulse noise or abnormal intensity pixels in an image can severely affect the accuracy of many algorithms. One way of overcoming this phenomenon is through analysis at various resolutions, often by then performing generalization akin to lossy compression in eliminating less significant information in the image, in order to emphasize the more significant regions. The most popular multiresolution tool is wavelets. There is much literature on the use of wavelets in noise reduction such as wavelet thresholding in [5] and [6], and for medical images such as ultrasound [7], and recently on MRI [8].

Multiscale Geometric Analysis (MGA)

Wavelets are localized and do well in one dimension - however, due to their poor orientation selectivity, wavelets do not represent higher-dimensional singularities effectively [9]. Directional wavelets and MGA are customized to enhance areas of interest, without being restricted to the horizontal and vertical directional limitations of conventional wavelets. Examples of MGA include curvelets [10], contourlets [11], ridgelets [10], the directional wavelet transform [12], as well as hybrid wavelets and directional filter banks (HWD) [13]. MGA have been applied successfully to various image processing problems including image compression [14], image enhancement [15], edge detection [16] and texture retrieval [17]. They are even used for adaptive denoising in the scale-space technique [18].

Curvelet

The curvelet is a mathematical tool for realizing the application of wavelets with "strong directional character in which elements are highly anisotropic at fine scales, with effective support shaped according to the parabolic scaling principle length² ∝ width" [9]. It may be represented by function (1) below:

$$\psi a,b,\theta (X)=a^{\frac{-3}{4}}\psi (D_a{R}_{\theta }(x-b))(1)$$

Where

a is the scale parameter (0 < a < 1),

b is the location,

θ is the orientation,

R_θ is a rotation by θ radians, and

D_a is a parabolic scaling matrix satisfying

$$D_a=\left(\begin{array}{cc}\frac{1}{a}& 0\\ 0& \frac{1}{\sqrt{a}}\end{array}\right)\text{ (2)}$$

The admissible profile is given by

$$(x_1,x_2)\in {ℝ}^2,\psi (x_1,x_2)\text{ (3)}$$

Candès states that an important property for curvelets is to obey the principle of harmonic analysis, such that it is possible to analyze and reconstruct an arbitrary function f (x1, x2) as a superposition of templates. It is possible to expand an arbitrary function f (x1, x2) as a series of curvelets, much like an expansion in an orthonormal basis.

Curvelets are said to be ideal for objects that are characterized by curve-punctuated smoothness - smoothness except for discontinuity along a general curve with bounded curvature - such as images with edges [9]. The curvelet transform has been used successfully in image denoising in [19].

From the sample MRCP images, it is observed that many parts of the bile ducts do display the above characteristics. As such, it is believed that curvelets may be effective in reducing the influence of the acquisition noise, overcoming parts of the low resolution images and in detecting the structures of interest in the MRCP images. Recently, curvelets have been used to identify colonic. The curvelet implementation in this paper uses the library from CurveLab [20], which implements the Fast Discrete Curvelet Transform.

Contourlet

Contourlets also known as pyramidal directional filter bank, are multiresolution directional tight frames designed to efficiently approximate images made of smooth regions separated by smooth boundaries. They have a fast implementation based on a Laplacian Pyramid decomposition followed by directional filter banks applied on each band pass sub band. Details and proof of the contourlet conception, as well as a comparison of wavelets vs. contourlets can be found in [21]. In the paper, the authors mention that from studies of the human visual system and natural image statistics, the desired "wish list" for image representations should be techniques that display the following characteristics: multiresolution (approximation from coarse to fine levels), localization (basis elements localized in spatial and frequency domains), critical sampling (basis or frame with small redundancy), directionality (basis oriented in various directions), and anisotropy (basis elements using elongated shapes with various aspect ratios). Contourlets were created to satisfy all five characteristics (cf. separable wavelets satisfy only the first three characteristics). Contourlets are able to represent smooth contours which appear very rectangular in separable wavelets.

Contourlets have been used in image denoising [22] and even in image watermarking [23]. It has been shown to produce superior denoising results as compared to wavelets in [24] due to its ability to preserve high gradient structures, minimizing statistical bias. The implementation in this paper utilizes the Contourlet Toolbox [25].

Ridgelet

The ridgetlet transform achieves very compact representation of linear singularities in images [26]. They rely on the Radon transform, which is a powerful tool to find directions where images present line features [26]. The continuous ridgelet transform proposed by [27] is given as follows:

$${\phi }_{a,b,\theta }(x)=a\frac{-1}{2}.\phi ((x_1\cos \theta +x_2\sin \theta -b)/a\text{ (4)}$$

Where $\phi (t)$ is the smooth function,

a is the scale parameter,

b is the location parameter,

θ is the orientation parameter

for the admissible condition

$${{\displaystyle \int {\left|\widehat{\phi }(\xi )\right|}^2/\left|\xi \right|}}^2\text{d}\xi <\infty and{\displaystyle \int \phi (t)dt=0}\text{ (5)}$$

and the forward transform is

$$R_f(a,b,\theta )={{\displaystyle \int \phi }}_{a,b,\theta }(x)f(x)dx\text{ (6) }$$

whilst the inverse transform is given by

$$f(x)={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{\infty }{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{R}_f}}}(a,b,\theta ){\phi }_{a,b,\theta }(x)\frac{da}{a^3}db\frac{d\theta }{4\pi }\text{ (7)}$$

The finite ridgelet transform (FRIT) is a discrete orthonormal version of the ridgelet transform. It is based on the finite radon transform (FRAT). FRIT, for a function f, can be written as [21]:

$$F{\text{ RIT}}_f[k,m]=\langle F{\text{ RAT}}_f[k,.],{\omega }_m^{(k)}[.]\rangle$$

$$\text{ = }\sum _{l\in Z_p}{\omega }_m^{(k)}[l]\langle f,{\phi }_{k,l}\rangle$$

$$\text{ = }\langle \text{f, }{\displaystyle \sum _{l\in Z_P}{\omega }_m^{(k)}}[l]{\phi }_{k,l}\rangle .\text{ (8)}$$

Where $\left\{{\phi }_{k,l}\right\}$ is the FRAT frame,

k and l are points that make up a line such that L_k,l would be a finite set of lines,

Z_p is a finite field with modulo p operations. Z_p² would be a lattice.

According to [28], the FRIT is only suitable for images of prime-pixels length. They have overcome this limitation through a new digital implementation of ridgelet transform that is suitable for images of dyadic length. In addition, the authors claim that not only are the main properties of the finite ridgelet preserved in their implementation, but the algorithm is also simplified.

A ridgelet kernel regression model has been proposed in [29] and has been shown to be robust, competitive in execution time and outperforms the support vector machine for a wide range of multivariate functions. Ridgelet neural networks have also been developed, such as the one based on the improved particle swarm optimization in [30]. The implementation in this paper utilizes the Ridgelet Toolbox [25].

Non-orthogonal wavelet denoising

A non-orthogonal wavelet-based denosing implementation by [3] is also tested in this paper for comparison. Unlike the conventional wavelet denoising implementations, this implementation is reported to preserve the phase information, which is vital to human perception. The convolutions are done via the Fast Fourier Transform (FFT) for speed. It also overcomes the common problem faced in typical orthogonal and bi-orthogonal wavelet applications, which is in determining the choice of wavelet to be used.

As discussed previously, denoising requires image analysis (usually by changing domains) and thresholding of the noise. This non-orthogonal wavelet method analyzes the image by convolving the signal with each of the quadrature pairs of wavelets. The responses of each quadrature pair produce the response vector.

$$[{\text{ e}}_n(x),o_n(x)\text{ ] = [I( x) }\ast {\text{ M}}_n^e,I(x)\ast {\text{M}}_{\text{n}}^{\text{0}}]\text{ (9)}$$

Where e_n(x) and o_n(x) are the real and binary parts of the complex valued frequency component, respectively; I is the signal; and $M_n^e{\text{ and M}}_n^O$ are the even- and odd-symmetric wavelets at scale n. The amplitude and phase of the transform at a scale are given as (10) and (11), respectively.

$$A_n(x)=\sqrt{e_n{(x)}^2+o_n{(x)}^2}\text{ (10)}$$

$${\Phi }_n(x)=a\tan 2(o_n(x),e_n(x))\text{ (11)}$$

For thresholding, the magnitude of response vectors would follow the Rayleigh distribution with a scale parameter of ${\sigma }_g$, and given as

$$R(x)=\frac{x}{{\sigma }_g^2}e\frac{-{\infty }^2}{2{\sigma }_g^2}\text{ (12)}$$

Taking the mean and variance of the distribution as (13) and (14), respectively, the threshold (T) is given by (15) with k in the range of 2-3

$${\mu }_{r={\sigma }_g}\sqrt{\frac{\pi }{2}}\text{ (13)}$$

$${\sigma }_r^2=\frac{4-\pi }{2}{\sigma }_g^2\text{ (14)}$$

$$T={\mu }_r+k{\sigma }_r\text{ (15)}$$

For robust estimation of the mean and amplitude measures above, the median of the Rayleigh distribution may be used, as explained in [3]. Thus, the threshold value is determined automatically and robustly for the input image.

Results and Discussion

The purpose of this work is to examine the performance of popular MGA pre-processing techniques applied for image noise reduction and enhancement of the ROI (i.e. the biliary structures) of the MRCP images. As described in the Introduction section, there are many issues with the clarity of MRCP images. Through experimental studies in the application of the various methods on the test samples, the results obtained are described in this section. The prescribed default settings of the respective toolboxes and code adapted from the demonstration files are used in this work in order to provide comparisons on the "native" performance of the algorithms. Once the actual target applications are known, the parameters may be tweaked accordingly.

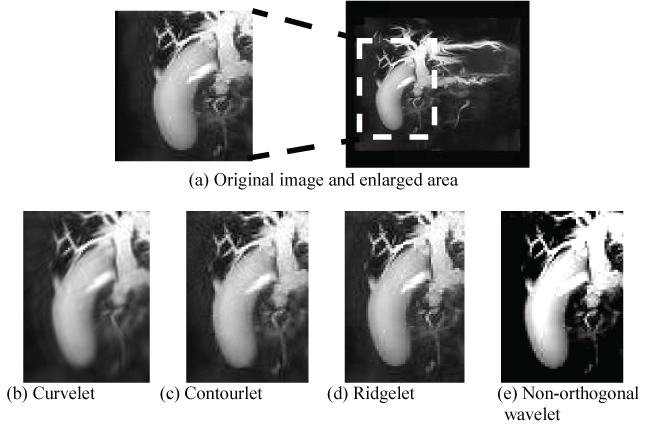
In order to analyze the performance, the tests conducted are categorized into various sets. The first set of results, as given in table 1, is for the images with a significant amount of noise influence, either due to the acquisition or background tissue. From the table, it is observed that the performance of the different methods varied significantly. This was expected due to the nature of the MRCP images and the suitability of the techniques based on specific characteristics. The ridgelet technique produced an almost exact reconstruction of the source image with no perceivable denoising for the MRCP test images. The contourlet effected some minimal smoothing of the texture, as observed in background tissue area (at the bottom left of all images and at the bottom right of the third test image). See figure 1 for a sample of the enlarged area and corresponding results. The curvelet achieved more perceivable smoothing and denoising on all the images. It successfully removed the impulse-like noise and smoothens the salt-and-pepper texture-type noise of the background tissue. This method of smoothing, however, does not necessarily improve the human visual perception and may defeat any consequent texture-based detection schemes. The automatic threshold determined by the non-orthogonal wavelet technique was significantly higher than those used by the MGA schemes, thus removing more noise. Inadvertently, the technique also removed some of the fine lower intensity biliary structures in the images.

As the MGA employed were based mainly on parabolic directional filters, the second test set was for images displaying more curve-like features, as given in table 2. From the results in the table as well as the enlarged parts of the significant curved area of the image in figure 2, it is seen that the ridgelet again produced an almost perfect reconstruction with little or no denoising. The contourlet’s slight smoothing was beneficial in this test case as it improved the continuity in the fine biliary branches in the images, as well as improved the consistency and texture of the circular objects (e.g. gallbladder). This would improve the subsequent structure detection processes. The curvelet’s heavier smoothing also achieved a similar effect, as these test images were not hindered by much background tissue influence. However, the edges in heavy smoothing are less defined and may adversely affect edge-detection algorithms. The non-orthogonal noise compensation wavelet implementation highlights the ROI, as well as allows for their edges to be featured more prominently. However, upon examining the fine biliary branches, it is observed that the integrity of the branches has been compromised as the connectivity is lost. Such a consequence may defeat localized image processing operations [1].

Finally, some thick slab MRCP images with almost no background influence were tested, as given in table 3. Although the performance characteristics described in the earlier two tests are present, they are not readily noticeable in this test set as the images lack fine structures and have good contrast between the ROI and the background. Ideally, the structure on the left (i.e. intestines) should be removed as it is not part of the bile ducts, but the limitation of an intensity-based greyscale image makes such a task impossible without further processing. Achieving such goals requires multi-level processing and structure identification, such as the segment-growing algorithm described in [2].

From the results of the various test sets, we can conclude that the decision on the most effective denoising technique for the MRCP images depends very much on the subsequent processing. The decision relies on knowledge of the anatomy as well as of the image processing techniques and range of coefficients that may be manipulated. The default common coefficients values chosen by the toolbox developers were used in this work as it would be a fair method of evaluating the schemes at their "optimal" settings. Trial and error, as well as detailed image and algorithm analysis would provide better outcomes than those presented here, but that is out of the scope of this work which serves as a preliminary exploration of the application of the popular MGA for denoising MRCP images without a specific target application.

Overall, the ridglet implementation performed badly as its thresholding ability was very poor for the noisy MRCP images. Its performance may be improved by manually setting the threshold value prior to the inverse transform. The contourlet provided sufficient denoising to eliminate minor influences of noise, aiding in improved structure detection. Such a technique would be the most practical for general-purpose denoising of MRCP images. The curvelet allowed for heavy smoothing, which is useful for establishing continuity in fine structures but reduces the prominence of edges. Unfortunately, it tends to compromise textural information and as such limits the range of applicable subsequent processing schemes. Finally, the non-orthogonal wavelet for noise compensation was effective in eliminating almost all the non-ROI noise (i.e. background tissue). It is useful as pre-processing for automatic identification of significant biliary structures, which is usually the case in the presence of diseases and for computer-aided diagnosis systems for biliary diseases [31], but is a liability for manual diagnosis as much structural information provided by the finer structures are lost.

The scope of the comparison in this work is limited to the visual results. This paper does not present technical metrics measurements, for example the calculation of SNR or root mean squared (RMS) error, as such metrics can bias the medical evaluation due to the mismatch between the human visual system and the technical metrics, as proven in [32]. The use of such metrics for greyscale images and their relevance to the human perception has also been criticized in [3,33,34]. As the result of this work is intended as pre-processing and enhancement of medical MRCP images to be used in diagnosis where decisions are made based on the visual interpretation, the results are presented accordingly without the bias of further technical results.

Conclusion

This paper has undertaken a preliminary survey of common MGA and explored their performance on a medical imaging modality, namely MRCP, which has become the defacto imaging modality for the diagnosis of diseases affecting the bile ducts and in the workup prior to liver surgery. Wavelets have long been shown to perform well in image denoising and compression tasks, but suffer from limited orientations. MGA have been introduced to overcome this problem, thus fulfilling the five characteristics expected of the human visual system and natural image statistics, namely, multiresolution, critical sampling, localization, directionality and anisotropy. Of this new generation of wavelets, the most common are curvelets, contourlets and ridgelets, which have been tested on in this work. Additional testing with a non-orthogonal wavelet developed for noise compensation has also been undertaken. The results show varying success rates and are applicable depending on the subsequent processing. Of particular interest for further analysis would be the contourlets for general-purpose denoising and the non-orthogonal wavelet for automatic disease detection.

In addition to the tested MGA, there exist other classes of MGA. These include beamlet, starlet, wedgelet [35], bandlet [36], brushlet [37], steerable wavelets [38], HWD [13], shearlet [39] and others. Some of these are described in [40] and further evaluation with these may also been explored in future to determine other possible denoising algorithms for MRCP images, where literature is scarce.

Acknowledgement

This work was supported by the Brain Gain Malaysia program under the Ministry of Science, Technology and Innovation, Malaysia as well as the Academy of Sciences, Malaysia.

References

1. Logeswaran R (2012) Improved Biliary Detection and Diagnosis through Intelligent Machine Analysis. Comput Methods Programs Biomed 107: 404-412.
2. Logeswaran R (2008) Reconstruction of biliary structure in 2D MRCP images using multi-scale analysis. Comput Biol Med 38: 391-400.
3. Kovesi P (1999) Phase preserving denoising of images. The Australian Pattern Recognition Society Conference: 212-217.
4. Gao X, Lu W, Tao D, et al. (2009) Image quality assessment based on multiscale geometric analysis. IEEE Trans Image Process 18: 1409-1423.
5. Jansen M (2001) Noise reduction by wavelet thresholding. Lecture Notes in Statistics. 161.
6. Zanchettin C, Ludermir TB (2007) Wavelet filter for noise reduction and signal compression in an artificial nose. Appl Soft Comput 7: 246-256.
7. Lázaro JC (2002) Noise reduction in ultrasonic NDT using discrete wavelet transform processing. IEEE Ultrasonics Symp: 777-780.
8. Schillaci T, Barraco R, Brai M, et al. (2007) Noise reduction in magnetic resonance images by wavelet transforms: an application to the study of capillary water absorption in sedimentary rocks. Magnetic Resonance Imag 25: 581-582.
9. Candès EJ (2003) What is a curvelet? Notices AMS 50: 1402-1403.
10. Candès EJ (1998) Ridgelets: theory and applications [PhD thesis]. Department of Statistics, Stanford University.
11. Do MN (2001) Directional multiresolution image representations [PhD thesis]. EPFL, Lausanne, Switzerland.
12. Heric D, Zazula D (2005) Reconstruction of object contours using directional wavelet transform. WSEAS Trans Comput 4: 1305-1312.
13. Eslami R, Radha H (2007) A new family of nonredundant transforms using hybrid wavelets and directional filter banks. IEEE Trans. Image Process 16: 1152-1167.
14. Miettinen K (2001) Application of directional wavelets to image compression. Proceedings of the Data Compression Conf: 505.
15. Heric D, Potocnik B (2006) Image enhancement by using directional wavelet transform. J Comp IT 14: 299-305.
16. Niya JM, Aghagolzadeh A (2004) Edge detection using directional wavelet transform. IEEE MELECON: 281-284.
17. Cheng KO, Law NF, Siu WC (2007) Multiscale directional filter bank with applications to structured and random texture retrieval. Patt Recogn 40: 1182-1194.
18. Jung CR, Scharcanski J (2001) Adaptative image denoising in scale-space using the wavelet transform. XIV Brazilian Symposium on Computer Graphics and Image Processing (SIBGRAPI'01): 172.
19. Starck JL, Candès EJ, Donoho DL (2002) The curvelet transform for image denoising. IEEE Trans Imag Process 11: 670-683.
20. Demanet L (2008) CurveLab 2.1.2.
21. Do MN, Vetterli M (2005) The contourlet transform: an efficient directional multiresolution image representation. IEEE Trans Image Process 14: 2091-2106.
22. Eslami R, Radha H (2003) The contourlet transform for image de-noising using cycle spinning. Asilomar Conf on Sig, Sys, and Comput: 1982-1986.
23. Song H, Yu S, Yang X, et al. (2008) Contourlet-based image adaptive watermarking. Image Commun 23: 162-178.
24. El Naqa I, Cui J, Lindsay P, et al. (2007) The denoising of Monte Carlo dose distributions using convolution superposition calculations. Phys Med Biol 52: N375-N385.
25. Do MN (2008) Software, Contourlet Toolbox and FRIT Toolbox.
26. Granai L (2002) Radon and ridgelet transform applied to motion compensated images. ITS Technical Report.
27. Candès EJ (1999) Harmonic analysis of neural networks. Appl Comput Harmon Anal 6: 197-218.
28. Jun XJ, Lin N, Miao Y (2005) A new digital implementation of ridgelet transform for images of dyadic length. Intl Conf on Info Tech and Appl (ICITA'05) 1: 613-616.
29. Yang S, Wang M, Jiao L, et al. (2005) A novel ridgelet kernel regression method. LNCS 3498: 893-899.
30. Su R, Kong L, Song S, et al. (2007) A new ridgelet neural network training algorithm based on improved particle swarm optimization. Third Intl Conf on Natural Computation (ICNC 2007).
31. Logeswaran R (2008) A computer-aided multi-disease diagnostic system using MRCP. J Dig Imaging 21: 235-242.
32. Choong MK, Logeswaran R, Bister M (2006) Improving diagnostic quality of MR images through controlled lossy compression using SPIHT. J Med Sys 30: 139-143.
33. Daly S (1993) The visible differences predictor: an algorithm for the assessment of image fidelity. In: Watson, Dig Images and Human Vis. MIT Press, 179-206.
34. Wilson D, Baddeley A, Owens R (1997) A new metric for grey-scale image comparison. Intl J Comput Vis 24: 5-17.
35. Donoho D (1999) Wedgelets: nearly minimax estimation of edges. Ann Statist 27: 859-897.
36. LePennec E, Mallat S (2005) Sparse geometric image representations with bandelets. IEEE Trans Image Process 14: 423-438.
37. Meyer F, Coifman R (1997) Brushlets: a tool for directional image analysis and image compression. Appl Comp Harm Anal 4: 147-187.
38. Freeman WT, Adelson EH (1991) The design and the use of steerable filters. IEEE Patt Anal Mach Intell 13: 891-906.
39. Wimmer G, Tamakic T, Tischendorfe JJW, et al. (2016) Directional wavelet based features for colonic polyp classification. Med Img Analy 31: 16-36.
40. Fuhr H, Demaret L, Friedrich Y (2006) Beyond wavelets: new image representation paradigms. In: Barni, Doc and Image Compression. Taylor & Francis, 179-205.