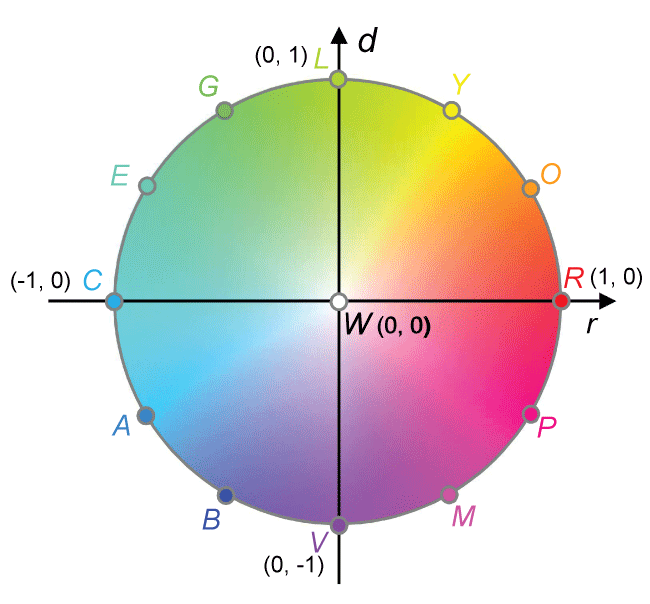Plotting Colors on Color Circle: Interconversion between XYZ Values and RGB Color System

Abstract

Color is generated by optical properties of the pigments. Colors can be calculated by using color matching functions. Color-measuring apparatus such as colorimeters and digital cameras also provide convenient ways to analyze object colors. Color values are given in three dimensions, as a result of these measurements. Such preliminary color values are then converted to the other values such as hue, saturation, lightness, and coordinates in two-dimensional color plates. Interestingly, two different but mutually correlated color systems (color coordinates) are used in colorimetry: XYZ colors and RGB colors. XYZ colors have been mainly used to calculate colors, whereas we recently succeeded to plot colors on color circle based on the measurement of RGB colors. RGB color system also has the advantage of the ease of understanding: RGB color values represent intensities of red, green, and blue colors. The advantages of XYZ color system are that colorimeters measure XYZ values, and the accumulation of XYZ data in past publications. To combine the advantages of XYZ and RGB color systems, we summarized, re-calculated, and partly devised formulae for interconversion between XYZ, RGB, and coordinates on color circle in this study. Our formulae, when combined with the formulae in previous reports, enabled to convert between all these values.

Introduction

We will recognize objects only by two factors in principle: shape and color; for example, 'green leaves' and 'red flowers'. As such, color of objects potentially has profound effects in both basic analytical studies and applications. Despite this significant importance of the analysis of colors (colorimetry), methods and theories in colorimetry are not fully understood, utilized, or developed by researchers. We will introduce the standard methods to measure and calculate colors first.

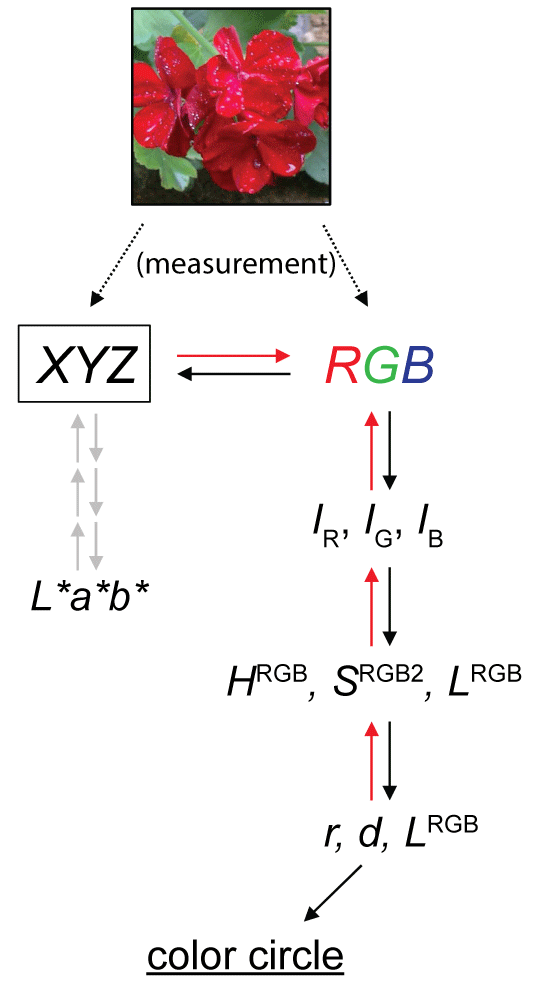
Figure 1 summarizes the ways how colors of objects are measured and calculated. Formally, colors are measured from surface reflectance spectra of opaque objects or transmittance spectra of transparent objects, R(λ). R(λ) spectra is measured by spectrophotometer such as UV-2450 (Shimadzu, Kyoto, Japan). Scientific definition of the range of 'visible light' is from 380 nm to 780 nm [1]. Then, R(λ) is measured from 380 nm to 780 nm at 5-nm intervals. Spectra (spectral power distribution) of incident lights (L(λ)) also should be taken in account. Their spectra are measured by spectroradiometer such as MS-720 (EKO Instruments, Kyoto, Japan). Thus, the spectra of light reflected/transmitted at the object and coming into our eyes (Spec(λ)) is the multiplication between R(λ) and L(λ) [2]:

$$Spec(\lambda )=R(\lambda )\cdot L(\lambda )\text{ (1)}$$

Transmittance of transparent objects are often measured as the absorbance values (Asb(λ)). Transmittance is calculated from absorbance as follows [2]:

$$R(\lambda )={10}^{-Abs(\lambda )}\text{ (2)}$$

Now we have the input data, Spec(λ), for color calculations.

Spec(λ) is converted to X, Y, and Z values in XYZ color space, or R, G, and B values in RGB color space by 'XYZ color matching functions' (x(λ), y(λ), and (z(λ)) or 'RGB color matching functions' (r(λ), g(λ), and (b(λ)), respectively. These color matching functions are not defined by formulae. Instead, values of the functions are given at 5-nm intervals, from 380 nm to 780 nm (Table 1) [1]. We also devised a standardized version of the RGB color matching functions (FR(λ), FG(λ), and FB(λ); (Table 1) [3]. Summation of the standardized RGB color matching functions along the whole range (380 nm - 780 nm) sums to unity (approximately 1). I_R, I_G, and I_B values are obtained by the standardized RGB color matching functions. These calculations are summarized as follows:

$X\text{ = }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot x(\lambda )$

$Y\text{= }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot y(\lambda )$

$Z\text{ = }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot z(\lambda )$

$R\text{ = }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot r(\lambda )$

$G\text{ = }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot g(\lambda )$

$B\text{ = }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot b(\lambda )$

$I_R\text{= }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot F_R(\lambda )$

$I_G\text{ = }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot F_G(\lambda )$

$I_B\text{ = }{\sum }_{(\lambda =380-780)}Spec(\lambda )\cdot F_B(\lambda )\text{ (3)}$

In the history of colorimetry, RGB color space was originally generated, then XYZ color space was later derived from RGB color space. Thus, R, G, and B values are converted to X, Y, and Z values in a three-dimensional matrix [1]:

$X\text{ = }2.768892\cdot R\text{+1}\text{.130160}\cdot B$

$Y\text{ = }1.000000\cdot R\text{+0}\text{.060100}\cdot B$

$Z\text{ = 0}\text{.000000}\cdot R\text{+5}\text{.594292}\cdot B\text{ (4)}$

XYZ color space is now more popular than RGB color space, but RGB color space is directly connected to our sense of colors: the three primary colors, i.e. red, green, and blue.

The most usual method of measuring object colors is not performed by color calculation with color matching functions, but by direct acquisition of X, Y, and Z values with colorimetric instruments. These instruments, such as CR-20 (Konica Minolta, Tokyo, Japan) measure X, Y and Z values in a moment, and automatically calculate XYZ-related coordinates such as L^*a^*b^* coordinates. Here, 'L^*a^*b^*' is also a color space, modified from XYZ color space so that the coordinates fit better with our sense of colors. The L^*a^*b^* color space is usually adopted to plot the measured object colors. It seems that the L^*a^*b^* color space is often considered to be a perfect color space, plotting all colors on a color circle at the even hue angles. Here, 'hue' represents the type of colors like red, green, and blue. There are also two other factors in colors: lightness (brightness) and saturation (vividness). Saturation is expressed as the distance from the origin, in color circle. Lightness is not expressed in color circle. With the lightness expressed as the third factor, color circle forms a color cylinder. Then, a^*-b^* color plate of the L^*a^*b^* color space is not actually a circle. Its shape is largely distorted from the circle, and the hues are not evenly placed around the origin. Accordingly, it is quite difficult to describe, on the a^*-b^* color plate, which hue angles correspond to specific colors such as red, orange, yellow, green, cyan, blue, and magenta. This inconsistency between the popular color measurements and the expected output data was found in our previous report [4].

Certainly, it is quite convenient to use colorimetric instruments to quickly and automatically obtain color coordinates, but there will be problems in these XYZ-based methodologies, when it comes to scientific description of object colors, and the compatibility of the obtained data with our sense of colors. For instance, response curves of colorimetric instruments manufactured by private companies are company secrets and never open to the public. It is easily imaginable that the response curves of these instruments are much different from the color matching functions, or otherwise resolution of light wave length may be greatly rough. Another problem is that the usually used L^*a^*b^* color space (or a^*-b^* color plate) is much distorted from the color circle, as described above.

An effective solution to these problems are direct calculation of object colors from reflectance/transmittance values, and going way back to the original RGB color system, from the modified XYZ color system [1-3]. In the RGB-based color coordinates, standardized values (I_R, I_G, and I_B) are directly calculated as in the formulae (3), or they are calculated from R, G, and B values:

$I_{\text{R}}=\text{R}/3.78204$

$I_{\text{G}}\text{ = }G/\text{3}\text{.7820}2$

$I_B=B/\text{3}\text{.78200}\text{ (5)}$

Thus, summations of I_R, I_G, or I_B along the whole range of visible wave lengths are almost unity (1.00003, 1.00000, or 0.99999; Table 1). It is not a strict measurement of colors, but RGB values which correspond to I_R, I_G, and I_B can be also easily recovered from digital photographs, by using the software like Adobe Photoshop. The RGB lightness (L^RGB) is calculated as follows:

$$L^{\text{GRB}}\text{ = }{I}_R+I_G+I_B\text{ (6)}$$

Relative proportions of I_R, I_G, and I_B $\rho ,\gamma ,$ and $\beta$ are also calculated:

$\rho =I_{\text{R}}/L^{\text{RGB}}$

$\gamma =I_{\text{G}}/L^{\text{RGB}}$

$\beta =I_{\text{B}}/L^{\text{RGB}}\text{ (7)}$

The RGB hue (H^RGB) is calculated from these values:

$\begin{array}{l}{H}^{\text{RGB}}=arctan2\text{(}\rho -\text{1/2}\cdot \gamma -\text{1/2}\cdot \beta ,\sqrt{3/2}\cdot \gamma -\sqrt{3/2}\cdot \beta \\ H^{\text{RGB}}=arctan2\text{(}\rho -\text{1/2}\cdot \gamma -\text{1/2}\cdot \beta ,\sqrt{3/2}\text{ (8)}\\ \end{array}$

The H^RGB values are given as angles in degrees. These angles are evenly distributed around the origin, and the abbreviations in single capital letters are given every 30°: red (R, 0°/360°); orange (O, 30°); yellow (Y, 60°); lawn (L, 90°); green (G, 120°); emerald (E, 150°); cyan (C, 180°); azure (A, 210°); blue (B, 240°); violet (V, 270°); magenta (M, 300°); pink (P, 330°). The origin is white (W), without any hue angle (Figure 2).

Calculation of the saturation values is not simple, because this is the biggest reason that causes distorted shapes of color plates. A preliminary value of the RGB saturation (S^RGB) is calculated from $\rho ,\gamma$ and $\beta$ values:

$$S^{\text{RGB}}=\text{1-3}\cdot min\text{(}\rho ,\gamma ,\beta )\text{ (9)}$$

The maximum values of S^RGB are almost unity between the hue angels of 0° and 120°, and between 240° and 360°, but they greatly exceed unity between 120° and 240°. This phenomenon is caused by the negative R values in highly saturated cyanic colors. The S^RGB values between 120° and 240° are approximated with the following formula (ASSCC; approximated saturation of saturated cyanic colors) [2]:

$ASSCC(H^{\text{RGB}})=\text{0}\text{.000000000203449043}\cdot {\text{(}{H}^{\text{RGB}})}^6$

$-0.000000227268920\cdot {\text{(}{H}^{\text{RGB}})}^5$

$+0.000104570141\cdot {\text{(}{H}^{\text{RGB}})}^4$

$-\text{ 0}\text{.0253372458}\cdot {\text{(}{H}^{\text{RGB}})}^3$

$+3.40502571\cdot {\text{(}{H}^{\text{RGB}})}^2$

$-240.288362\cdot H^{RGB}$

$+\text{ 6950}\text{.26771 (10)}$

Then, the RGB saturation is rounded to realize the unity of the maximum values (S^RGB2) with ASSCC (H^RGB):

$S^{RGB2}=S^{RGB}{\text{ (0}}^{\circ }\le H^{RGB}\le {120}^{\circ },{\text{ 240}}^{\circ }\le H^{RGB}\le {\text{ 360}}^{\circ })$

$S^{RGB2}=S^{RGB}/ASSCC\text{(}{H}^{RGB}){\text{ (120}}^{\circ }<H^{RGB}<{240}^{\circ })\text{ (11)}$

The RGB values recovered from digital photographs do not have negative values, then this calculation with ASSCC will not be necessary for such data.

To summarize, S^RGB2, H^RGB, and L^RGB values represent evenly distributed colors on the color circle (or in the color cylinder), which perfectly fit with our sense of colors. Color coordinates on the color circle (r-d coordinates on the round color diagram) are as follows (Figure 2):

$r=S^{RGB2}\cdot cos{H}^{RGB}$

$d=S^{RGB2}\cdot sin{H}^{RGB}\text{ (12)}$

As shown in the Figure 1, several steps of mathematical conversions are necessary to calculate each colorimetric value. These mathematical conversions have been one-directional: the upstream values such as RGB and XYZ are calculated to obtain downstream values such as L^*a^*b^*and r-d coordinates. The formulae for calculations in reverse directions are not described in previous literatures. In the present study, we will derive the formulae to calculate in reverse directions. These formulae enable interconversion between RGB values, XYZ values, and r-d coordinates (i.e. plots on the color circle).

Materials and Methods

Calculation of the inverse 3 × 3 matrix

Inverse 3 × 3 matrices can be calculated by a formula. Instead of using the formula, we input data into a website [5] which automatically calculated the inverse 3 × 3 matrix.

Measurement of the leaf color

Leaves were excised from cherry blossom tree (Prunus sp. cultivar 'Taoyame') in spring. The XYZ values of five leaves were measured with CD100 colorimeter (Yokogawa Meters & Instruments Corp, Tokyo, Japan), and the median value (third largest value of the five measurements) was used for calculations.

Results

Interconversion between XYZ and RGB values

The X, Y, and Z values are calculated from R, G, and B values as in the formulae (4). Formulae (4) form a 3 × 3 matrix, then the inverse matrix of the formulae (4) immediately derives the following formulae:

$R=\text{ 0}\text{.418455}\cdot X-0.158657\cdot Y-\mathrm{0.082832.}Z$

$G=\text{ -0}\text{.091165}\cdot X\text{+0}\text{.252426}\cdot Y\text{+0}\text{.015705}\text{.}Z$

$B\text{ = 0}\text{.000921}\cdot X\text{-0}\text{.002550}\cdot Y+0.178595\cdot Z\text{ (13)}$

By using these formulae, now it is possible to convert XYZ values, which were measured in colorimetric instruments, to RGB values. Interconversion between XYZ values and L^*a^*b^* coordinates is not the target of this study, but this interconversion will be also possible.

Reverse calculation of H^RGB and S^RGB2 from r-d coordinates

The r-d coordinates are the positions on the color circle, and calculated from H^RGB and S^RGB2 by the formulae (12). The back calculations of H^RGB and S^RGB2 from the r-d coordinates are simple, just following the standard trigonometric functions. H^RGB is the angle of the line connecting between r-d coordinates and the origin. S^RGB2 is the distance of the r-d coordinates from the origin:

$H^{RGB}=arctan2\text{ (r, d)}$

$S^{RGB}{}^2=\sqrt{r^2+d^2}\text{ (14)}$

The lightness value is not reflected in the plots on the color circle, so the value of L^RGB cannot be calculated from the r-d coordinates. The lightness values should be prepared separately, or alternatively, the colors are simply calculated without lightness values.

S^RGB is back calculated from S^RGB2 as follows:

$S^{RGB2}\text{ = }{S}^{RGB}{\text{(0}}^{\circ }\le H^{RGB}\le {120}^{\circ },{\text{ 240}}^{\circ }\le H^{RGB}\le {\text{360}}^{\circ })$

$S^{RGB2}=S^{RGB}\cdot ASSCC\text{(}{H}^{RGB}){\text{ (120}}^{\circ }<H^{RGB}<{240}^{\circ })\text{ (15)}$

Reverse calculation of RGB values from H^RGB, S^RGB, and L^RGB

The H^RGB and S^RGB values obtained above are first converted to $\rho ,\gamma$ and $\beta$ values. This calculation is performed in simultaneous equations, consisting of three first-degree equations. First, the values of $\rho ,\gamma$ and $\beta$ always sum to unity:

$$\rho +\gamma +\beta =\text{ 1 (16)}$$

Second, the H^RGB is an arctangent value calculated in the formula (8). Then, its back calculation is as follows:

$tan{H}^{RGB}=\text{ (}\sqrt{3/2}\cdot \gamma -\sqrt{3/2}\cdot \beta )/\text{ (}\rho -1/2\cdot \lambda -1/2\cdot \beta )$

This formula is transformed as:

$$tan{H}^{RGB}\cdot (2\rho -\gamma -\beta )=\sqrt{3\cdot }(\gamma -\beta )\text{ (17)}$$

Third, S^RGB was calculated from the minimum value among $\rho ,\gamma$ and $\beta$ in the formula (9). The minimum value among these three values is determined by the hue angles. Thus, the back calculation of the formula (9) is:

$S^{RGB}=\text{ 1-3}\beta {\text{ (0}}^{\circ }\le H^{RGB}\le {120}^{\circ })$

$S^{RGB}=\text{ 1-3}\rho {\text{ (120}}^{\circ }<H^{RGB}<{240}^{\circ })$

$S^{RGB}=\text{ 1-3}\gamma {\text{ (240}}^{\circ }\le H^{RGB}\le {\text{360}}^{\circ })\text{ (18)}$

Calculating the simultaneous equations (16), (17), and (18) gives $\rho ,\gamma$ and $\beta$ values. Then, I_R, I_G, and I_B values are:

$I_R\text{ = }\rho \cdot {\text{L}}^{RGB}$

$I_G=\gamma \cdot {\text{L}}^{RGB}$

$I_B=\beta \cdot {\text{L}}^{RGB}\text{ (19)}$

Finally, R, G, and B values are:

$R=\text{ 3}\text{.78204}\cdot {\text{I}}^{\text{R}}$

$G=\text{ 3}\text{.7820}2\cdot {\text{I}}^{\text{G}}$

$B=\text{ 3}\text{.7820}0\cdot {\text{I}}^{\text{B}}\text{ (20)}$

Example of color calculation

An example of the calculation of the RGB-based colorimetric values from an XYZ data set will be demonstrated here, for better understanding of the calculations.

An XYZ data set was measured with a colorimeter, on a leaf of cherry blossom tree (Figure 3). These values were (X, Y, Z) = (5.420, 7.965, 2.077). This data set was converted to RGB data set by using the formulae (13), obtaining the values (R, G, B) = (0.8322, 1.5492, 0.3556). By using the formulae (5), these values were standardized, so that (I_R, I_G, I_B) = (0.2200, 0.4096, 0.0940). Sum of these values represents the RGB lightness, according to the formula (6), then (L^RGB) = (0.7237). Following the formulae (7), ratios of I_R, I_G, and I_B are: I_R, I_G, and I_B = (0.3041, 0.5660, 0.1299).

The H^RGB and S^RGB values are calculated with formulae (8) and formulae (9): (H^RGB, S^RGB) = (96.6°, 0.6102). At this angle of H^RGB, S^RGB2 is the same as S^RGB formulae (11): (S^RGB2) = (0.6102). At last, the r-d coordinate is calculated by the formulae (12): (r, d) = (-0.070,0.606).

Discussion

RGB-based color of the cherry leaf

As an example of color calculation, we measure and calculated the color of a cherry leaf. Here, how are the RGB-based colorimetric values estimated, in the terms of colorimetry? Let us check the meaning of each colorimetric value one by one.

To begin with, the values of I_R, I_G, and I_B were approximately 0.22, 0.41, and 0.09, respectively. Because these values have been standardized so that the maximum value is 1, these values mean that the color of this leaf is interpreted as the mixture of 22% strength red light, 41% strength green light, and 9% strength blue light. At this point, we can deduce that this color is greenish, but a bit yellowish. L^RGB value was 0.72. Considering that the maximum value of L^RGB is 3, the leaf is not so much blight. These speculations would be consistent with the true color of this leaf (Figure 3).

The color profile is completely clear with the H^RGB and the S^RGB2 values. The H^RGB value was 97°. This hue angle is a bit more greenish that the lawn color (L; yellow-green; 90°). S^RGB2 value was 0.61, representing that the color is 61% vivid compared with the full saturation value. With the r-d coordinate of (-0.07, 0.61), the color of this leaf is plotted at this position on the unit color circle (Figure 2).

Interconversion between colorimetric values

In this study, we calculated the formulae to convert XYZ values to RGB values. This important calculation is not mentioned for the first time in this study. The formulae to convert XYZ values to RGB values have been reported in past publications [6,7], but these formulae are different from each other. This is probably because different versions of XYZ and/or RGB color matching functions were used to derive these formulae. We then re-calculated the formulae, based on seemingly the most standard XYZ and RGB color matching functions, by showing their values in Table 1. The resulting formulae (13) were quite similar to the ones on a website [7]. Thus, it was confirmed that the formulae (13) and the formulae on the website are suitable for conversion of the standard XYZ values to the standard RGB values.

Because object colors are usually measured as XYZ colors, such colorimetric data has been almost always plotted onto the XYZ-related color plates, such as the a^*-b^* color plate [8,9]. Our formulae for conversion of the XYZ values to the RGB values connected these color systems each other, and enabled to calculate the coordinates on the color circle, even from the XYZ values. Unlike the largely distorted XYZ-based color plates, the RGB-based color circle and the colorimetric values can be readily interpreted to color names, such as orange and purple [10]. From now on, researchers calculating object colors by either XYZ values or RGB values are recommended to calculate RGB-based colorimetric values, and plot colors on the color circle.

We also derived a series of formulae to back calculate RGB values from the coordinates on the color circle. These calculations are relatively complicated, but possible. By using these formulae, for example, the proportions of three primary colors (red, green, and blue) can be identified for any part of the color circle. This will help generating specific colors by mixture of lamps with different visible light spectra. As we reported in previous papers, colorimetric effects such as 'dichromatism' and 'alexandrite effect' can be also analyzed by following rigid spectral calculations [2,3]. These are just examples of possible applications, and the relationship between the whole colorimetric values, clarified in this study, potentially contributes to any aspect of colorimetric analyses.

References

1. (2004) Colorimetry. (3^rd edn), Commission Internationale de l'Eclairage, CIE Publ 15, Vienna.
2. Kasajima I (2016) Alexandrite-like effect in purple flowers analyzed with newly devised round RGB diagram. Sci Rep 6: 29630.
3. Kasajima I, Sasaki K (2014) Dichromatism causes color variations in leaves and spices. Color Res Appl 40: 605-611.
4. Kasajima I, Fekih R (in press) Eating colors: a scientifically based perception of food colors. Jacobs J Food Nutr.
5. http://keisan.casio.jp/exec/system/1278758277.
6. Hunt RWG, Pointer MR (2011) RGB Colorimetry. Measuring colour. Wiley, Hoboken, USA.
7. https://en.wikipedia.org/wiki/CIE_1931_color_space
8. Katsumoto Y, Fukuchi-Mizutani M, Fukui Y, et al. (2007) Engineering of the rose flavonoid biosynthetic pathway successfully generated blue-hued flowers accumulating delphinidin. Plant Cell Physiol 48: 1589-1600.
9. Noda N, Aida R, Kishimoto S, et al. (2013) Genetic engineering of novel bluer-colored chrysanthemums produced by accumulation of delphinidin-based anthocyanins. Plant Cell Physiol 54: 1684-1695.
10. Kasajima I, Ohtsubo N, Sasaki K (2017) Combination of Cyclamen persicum Mill. floral gene promoters and chimeric repressors for the modification of ornamental traits in Toreniafournieri Lind. Hort Res 4: 17008.